Eliminando la recursividad por la izquierda. Análisis Eliminar recursividad izquierda en línea
Clasificación de gramáticas formales según Chomsky
· Gramática de tipo 0 (forma general). Las reglas tienen la forma α→β
· Gramática tipo 1 (dependiente del contexto, KZ)
Las reglas tienen la forma αAβ → αγβ. γ pertenece a V +, es decir la gramática no se trunca
α,β se llaman contexto izquierdo y derecho
· Gramática tipo 2 (libre de contexto, KS)
Las reglas son de la forma A → α. α pertenece a V*, es decir la gramática se puede acortar => los idiomas KS no están contenidos en KS
Más cercano al BPF
· Gramática tipo 3 (automática, regular)
Las reglas son de la forma A → aB, A → a, A → ε
Los idiomas automáticos están contenidos en los idiomas KS.
Ejemplo. Una gramática que genera un lenguaje de expresiones regulares entre paréntesis.
S → (S) | SS | ε
Generación (inferencia)
Designaciones
=>+ (1 o más)
=>* (0 o más)
Forma oracional de gramática es una cadena que se puede derivar del carácter inicial.
Oración (sentimiento) de gramática es una forma oracional que consta únicamente de terminales.
Gramática del lenguaje L(G)-Este es el conjunto de todas sus propuestas.
Designaciones:
Salida izquierda, derecha (generación).
Salida izquierda y derecha para la oración i + i * i
El árbol de salida (árbol sintáctico, árbol de análisis) de una cadena de oraciones. A diferencia de la generación, de ella se excluye la información sobre el orden de inferencia.
Analizar la copa del árbol: cadena de marcas de hojas de izquierda a derecha
Una gramática que produce más de un árbol de análisis para una oración se llama ambiguo.
Un ejemplo de gramática ambigua. Gramática de expresiones aritméticas.
mi → mi+mi | E*E | i
Dos árboles de análisis para la cadena i + i * i
Un ejemplo de gramática ambigua. Gramática de declaraciones condicionales
S → si b entonces S
| si b entonces S si no S
Dos árboles de análisis para la cadena si b entonces si b entonces a
Convertir a gramática inequívoca equivalente:
S → si b entonces S
| si b entonces S2 sino S
S2 → si b entonces S2 si no S2
44. Lenguajes formales y gramáticas: lenguajes no vacíos, finitos e infinitos
45.Equivalencia y minimización de autómatas.
Equivalencia de máquinas de estados finitos
Sea S un alfabeto (un conjunto finito de símbolos) y S* el conjunto de todas las palabras del alfabeto S. Denotemos por e una palabra vacía, es decir no contiene letras (símbolos de S) en absoluto, sino el signo ×: la operación de asignar (concatenar) palabras.
Entonces, aav × va = aavva. A menudo se omite el signo × de la operación de atribución.
Las palabras del alfabeto S se denotarán con letras griegas minúsculas a, b, g, .... Obviamente, e es la unidad para la operación de atribución:
También es obvio que la operación de atribución es asociativa, es decir (ab)g = a(bg).
Así, el conjunto S* de todas las palabras del alfabeto S con respecto a la operación de asignación es un semigrupo con identidad, es decir monoide;
S* se llama monoide libre sobre el alfabeto S.
Minimización de la máquina de estados
Diferentes máquinas de estados pueden funcionar de manera idéntica, incluso si tienen numero diferente estados. Una tarea importante es encontrar una máquina de estados finitos mínima que implemente un mapeo de autómata determinado.
Es natural llamar equivalentes a dos estados de un autómata, que no pueden distinguirse mediante ninguna palabra de entrada.
Definición 1: Dos estados p y q de una máquina de estados finitos
A = (S,X,Y,s0,d,l) se llaman equivalentes (denotados por p~q) si ("aО X*)l*(p,a) =l*(q, a)
46. Equivalencia de las máquinas de Turing de cinta única y de cinta múltiple
Es obvio que el concepto de MT de k-tape es más amplio que el concepto de máquina de cinta única "normal". DEFINICIÓN 6. La máquina de cintas (k+1) M′ con el programa w simula la máquina de cintas k M si para cualquier conjunto de palabras de entrada (x1, x2,…, xk) el resultado del trabajo M′ coincide con el resultado del trabajo M en los mismos datos de entrada. Se supone que la palabra w se escribe por primera vez en la (k+1)ésima cinta M′. El resultado se entiende como el estado de las primeras k cintas MT en el momento de la parada, y si M no se detiene en una entrada determinada, entonces la máquina que lo simula tampoco debería detenerse en esta entrada.
DEFINICIÓN 7. Una cinta (k+1) MT M* se denomina máquina de Turing universal para máquinas de cintas k si para cualquier máquina de cintas k M existe un programa w en el que M* simula M. 12 Tenga en cuenta: en la definición de un MT universal la misma máquina M′ debe simular diferentes máquinas de cinta k (en diferentes programas w). Considere el siguiente teorema. TEOREMA 3. Para cualquier k≥1 existe una máquina de cinta de Turing universal (k+1). Prueba. Demostremos el teorema de manera constructiva, es decir le mostraremos cómo puede construir lo requerido coche universal METRO*. Consideremos sólo el esquema general de construcción, omitiendo detalles complejos. La idea principal es colocar una descripción de la máquina de Turing simulada en una cinta adicional (k+1)-ésima y utilizar esta descripción durante el proceso de simulación.
DEFINICIÓN 8. Diremos que la máquina de Turing M calcula función parcial f:A*→A*, si para cualquier x∈A* escrito en la primera cinta de la máquina M: si se define f(x), entonces M se detiene, y en el momento de detenerse la palabra f(x) es escrito en la última cinta de la máquina; Si f(x) no está definida, entonces la máquina M no se detiene.
DEFINICIÓN 9. Diremos que las máquinas M y M′ son equivalentes si calculan la misma función. El concepto de equivalencia es “más débil” que el de simulación: si una máquina M′ simula una máquina M, entonces la máquina M′ es equivalente a M; lo contrario, en términos generales, no es cierto. Por otro lado, la simulación requiere que M′ tenga al menos tantas cintas como M, mientras que la equivalencia no requiere 15. Es esta propiedad la que nos permite formular y demostrar el siguiente teorema.
TEOREMA 4. Para cualquier máquina de k-cintas M con complejidad temporal T(n), existe una máquina equivalente de una cinta M′ con complejidad temporal T′ (n) = O(T 2 (n)).
48. Transformaciones equivalentes de gramáticas KS: exclusión de reglas de cadena, eliminación de una regla gramatical arbitraria
Definición. Regla gramatical amable , Dónde , VA se llama cadena.
Declaración. Para una gramática KS Γ que contiene reglas en cadena, es posible construir una gramática equivalente Γ" que no contenga reglas en cadena.
La idea de la prueba es la siguiente. Si el esquema gramatical tiene la forma
R = (..., ,...,
entonces tal gramática es equivalente a una gramática con un esquema
R" = (..., a
ya que la salida en la gramática con el diagrama de circuito R de la cadena a
se puede obtener en una gramática con el esquema R" usando la regla a
En general, la prueba del último enunciado se puede realizar de la siguiente manera. Dividamos R en dos subconjuntos R 1 y R 2, incluyendo en R 1 todas las reglas de la forma
Para cada regla de R 1 encontramos un conjunto de reglas S( ), que se construyen así:
Si *y en R 2 hay una regla α, donde α es la cadena del diccionario (V t V A)*, luego en S( ) habilitar la regla
Construyamos nuevo esquema R" combinando las reglas R 2 y todos los conjuntos construidos S( ). Obtenemos una gramática "G" = (V t, V A , I, R"), que es equivalente a la dada y no contiene reglas de la forma .
Como ejemplo, realicemos la excepción de reglas de cadena de la gramática de G 1.9 con el esquema:
R=(
Primero, dividamos las reglas gramaticales en dos subconjuntos:
R 1 = (
R2 = (
Para cada regla de R 1 construimos un subconjunto correspondiente.
S(
S(
Como resultado, obtenemos el esquema gramatical deseado sin reglas en cadena en la forma:
R2U S(
El último tipo de transformación considerado está asociado con la eliminación de reglas con el lado derecho vacío de la gramática.
Definición. regla amable $ se llama regla anuladora.
49.Transformaciones equivalentes de gramáticas KS: eliminación de símbolos inútiles.
Dejemos que se dé una gramática KS arbitraria GRAMO . No terminal A esta gramática se llama productivo , si hay una cadena de terminales (incluida una vacía) tal que A Þ * a improductivo.
Teorema. Cada gramática CS es equivalente a una gramática CS sin no terminales improductivos.
No terminal A gramática GRAMO llamado realizable , si tal cadena existe a , Qué S Þ * a . De lo contrario, el no terminal se llama inalcanzable.
Teorema. Cada gramática KS es equivalente a una gramática KS sin no terminales inalcanzables.
Un símbolo no terminal en una gramática KS se llama inútil (o redundante) , si es inalcanzable o improductivo.
Teorema. Cada gramática CS es equivalente a una gramática CS en la que no hay no terminales inútiles.
Ejemplo. Eliminar símbolos inútiles en gramática
S® CA | A; A ® taxi; B ® b ; C ® a.
Paso 1. estamos construyendo mucho realizable caracteres: {S} ® { S, C, A}® { S, C, A, B}. Todos los no terminales son accesibles. No hay inalcanzables, la gramática no cambia.
Paso 2. estamos construyendo mucho productivo caracteres: {C, B}® { S, C, B}. lo entendemos A - no productivo. Lo eliminamos de la gramática y todas las reglas que lo acompañan. Obtenemos
S® CA; B ® b ; C ® a.
Paso 3. estamos construyendo mucho realizable símbolos de la nueva gramática: {S} ® { S, C}. lo entendemos B inalcanzable. Lo eliminamos de la gramática junto con todas las reglas que lo acompañan. Obtenemos
S® CA; C ® a.
Este es el resultado final.
50. Transformaciones equivalentes de gramáticas KS: eliminación de recursividad por la izquierda, factorización por la izquierda
Eliminando la recursividad hacia la izquierda
La principal dificultad al utilizar el análisis predictivo es encontrar una gramática para el lenguaje de entrada que pueda usarse para construir una tabla de análisis con entradas definidas de forma única. A veces, con algunas transformaciones simples, una gramática que no es LL(1) se puede reducir a una gramática LL(1) equivalente. Entre estas transformaciones, las más efectivas son la factorización por la izquierda y la eliminación. recursividad izquierda. Es necesario señalar aquí dos puntos. En primer lugar, no todas las gramáticas se vuelven LL(1) después de estas transformaciones y, en segundo lugar, después de tales transformaciones la gramática resultante puede volverse menos comprensible.
La recursividad directa hacia la izquierda, es decir, la recursividad del formulario, se puede eliminar de la siguiente manera. Primero agrupamos las reglas A:
donde ninguna de las cadenas comienza con A. Luego reemplazamos este conjunto de reglas con
donde A" es un nuevo no terminal. Del no terminal A puedes derivar las mismas cadenas que antes, pero ahora no puedes recursividad izquierda. Este procedimiento elimina todos los directos recursiones izquierdas, pero no se elimina la recursividad hacia la izquierda que involucra dos o más pasos. Dada a continuación algoritmo 4.8 te permite borrar todo recursiones izquierdas desde la gramática.
factorización izquierda
La idea principal de la factorización por la izquierda es que en el caso en el que no está claro cuál de las dos alternativas debe usarse para expandir un A no terminal, es necesario cambiar las reglas A para posponer la decisión hasta que haya suficiente información para tomar la decisión correcta.
Si 
- dos reglas A y la cadena de entrada comienza con una cadena no vacía, la salida no sabemos si expandirnos de acuerdo con la primera regla o la segunda. Puedes aplazar la decisión ampliando . Luego, después de analizar de qué es deducible, puedes ampliar por o por . Las reglas factorizadas por la izquierda toman la forma
51. Lenguaje de máquina de Turing.
La máquina de Turing incluye un ilimitado en ambas direcciones. cinta(Son posibles máquinas de Turing que tengan varias cintas infinitas), divididas en celdas, y dispositivo de control(también llamado cabeza de lectura-escritura (GZCH)), capaz de estar en uno de conjunto de estados. El número de estados posibles del dispositivo de control es finito y está especificado con precisión.
El dispositivo de control puede moverse hacia la izquierda y hacia la derecha a lo largo de la cinta, leer y escribir caracteres de algún alfabeto finito en celdas. Destaca especial vacío un símbolo que llena todas las celdas de la cinta, excepto aquellas (el número final) en las que están escritos los datos de entrada.
El dispositivo de control funciona según reglas de transición, que representan el algoritmo, realizable esta máquina de Turing. Cada regla de transición le indica a la máquina, dependiendo del estado actual y del símbolo observado en la celda actual, que escriba en esta celda. nuevo símbolo, vaya a un nuevo estado y mueva una celda hacia la izquierda o hacia la derecha. Algunos estados de la máquina de Turing pueden etiquetarse como Terminal, y pasar a cualquiera de ellos significa el final del trabajo, deteniendo el algoritmo.
Una máquina de Turing se llama determinista, si cada combinación de estado y símbolo de cinta en la tabla corresponde como máximo a una regla. Si hay un par "símbolo de cinta - estado" para el cual hay 2 o más instrucciones, dicha máquina de Turing se llama no determinista.
Gramática LL(k) si, para una cadena dada y los primeros k caracteres (si los hay) resultantes de , hay como máximo una regla que se puede aplicar a A para obtener la salida de alguna cadena terminal,
Arroz. 4.4.
comenzando y continuando con los k terminales mencionados.
Una gramática se llama gramática LL(k) si es una gramática LL(k) para algún k.
Ejemplo 4.7. Considere la gramática GRAMO = ((S, A, B), (0, 1, a, b), P, S), donde P consta de reglas
S->A | B, A -> aAb | 0, B -> aBbb | 1.
Aquí . G no es una gramática LL (k) para ningún k. Intuitivamente, si comenzamos leyendo una cadena de caracteres lo suficientemente larga a , no sabemos cuál de las reglas S -> A y S -> B se aplicó primero hasta que encontramos 0 o 1 .
Direccionamiento definición precisa LL (k) -gramáticas, ponga y y = a k 1b 2k . Luego conclusiones
corresponden a las conclusiones (1) y (2) de la definición. Los primeros k caracteres de las cadenas xey son iguales. Sin embargo, la conclusión es falsa. Dado que aquí k se elige arbitrariamente, G no es una gramática LL.
Consecuencias de la definición de gramática LL(k)
Teorema 4.6. gramática KS es una gramática LL(k) si y sólo si para dos reglas diferentes y desde la intersección P vacío con todos estos , Qué 
.
Prueba. Necesidad. Supongamos que y satisface las condiciones del teorema, y contiene x . Entonces, según la definición de PRIMERO, para algunos y y z hay conclusiones
(Obsérvese que aquí hemos aprovechado el hecho de que N no contiene no terminales inútiles, como se supone para todas las gramáticas consideradas.) Si |x|< k ; то y = z = e . Так как , то G не LL (k)- грамматика .
Adecuación. Supongamos que G no es una gramática LL(k).
Entonces hay dos conclusiones.
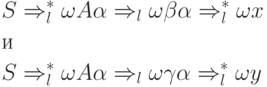
que las cadenas x e y coinciden en las primeras k posiciones, pero . Es por eso - reglas diferentes de P y cada uno de los conjuntos 
Y 
contiene la cadena PRIMERO k(x) coincidiendo con la cadena PRIMERO k(y).
Ejemplo 4.8. Una gramática G que consta de dos reglas S -> aS | a no será una gramática LL(1), ya que
PRIMERO 1 (aS) = PRIMERO 1 (a) = a.
Intuitivamente, esto se puede explicar de la siguiente manera: al ver solo este primer carácter al analizar una cadena que comienza con el símbolo a, no sabemos cuál de las reglas S -> aS o S -> a debe aplicarse a S. Por otro lado, G es una gramática LL(2). De hecho, en la notación del teorema que acabamos de presentar, si , entonces A = S y . Como sólo se dan las dos reglas indicadas para S, entonces . Dado que FIRST2(aS) = aa y FIRST2(a) = a, entonces, según el último teorema, G será una gramática LL (2).
Eliminando la recursividad hacia la izquierda
La principal dificultad al utilizar el análisis predictivo es encontrar una gramática para el lenguaje de entrada que pueda usarse para construir una tabla de análisis con entradas definidas de forma única. A veces, con algunas transformaciones simples, una gramática que no es LL(1) se puede reducir a una gramática LL(1) equivalente. Entre estas transformaciones, las más efectivas son la factorización por la izquierda y la eliminación de la recursividad por la izquierda. Es necesario señalar aquí dos puntos. En primer lugar, no todas las gramáticas se vuelven LL(1) después de estas transformaciones y, en segundo lugar, después de tales transformaciones la gramática resultante puede volverse menos comprensible.
La recursividad directa hacia la izquierda, es decir, la recursividad del formulario, se puede eliminar de la siguiente manera. Primero agrupamos las reglas A:
donde ninguna de las líneas comienza con A . Luego reemplazamos este conjunto de reglas con
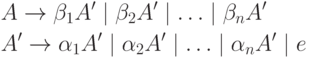
donde A" es el nuevo no terminal. Se pueden deducir las mismas cadenas del no terminal A que antes, pero ahora no hay recursividad por la izquierda. Este procedimiento elimina todas las recursividades por la izquierda inmediatas, pero no elimina la recursividad por la izquierda que involucra dos o más pasos. Dado abajo algoritmo 4.8 le permite eliminar todas las recursiones izquierdas de la gramática.
Algoritmo 4.8. Eliminando la recursividad hacia la izquierda.
Entrada. Gramática KS G sin reglas e (de la forma A -> e ).
Salida. Gramática KS G" sin recursividad por la izquierda, equivalente a G.
Método. Siga los pasos 1 y 2.
(1) Ordene los no terminales de la gramática G en cualquier orden.
(2) Realice el siguiente procedimiento:
Después de la (i-1)ésima iteración del bucle exterior en el paso 2 para cualquier regla de la forma 
, donde k< i
, выполняется s >k. Como resultado, en la siguiente iteración (por i), el bucle interno (por j) aumenta sucesivamente el límite inferior de m en cualquier regla. 
, hasta que haya m >= i . Luego, después de eliminar la recursividad izquierda inmediata para las reglas Ai, m se vuelve mayor que i.
Una gramática que contiene recursividad hacia la izquierda no es una gramática LL(1). Veamos las reglas.
A→ Automóvil club británico(recursión izquierda en A)
A→ a
Aquí a símbolo predecesor para ambas variantes no terminales A. De manera similar, una gramática que contiene un bucle recursivo izquierdo no puede ser una gramática LL(1), por ejemplo
A→ ANTES DE CRISTO.
B→ CD
C→ A.E.
Una gramática que contiene un bucle recursivo por la izquierda se puede convertir en una gramática que contiene sólo la recursión por la izquierda directa y luego, introduciendo no terminales adicionales, la recursividad por la izquierda se puede eliminar por completo (de hecho, se reemplaza por la recursividad por la derecha, lo cual no es un problema con respecto a LL(1) -propiedades).
Como ejemplo, considere una gramática con reglas generativas.
S→ Automóvil club británico
A→ Cama y desayuno
B→ cc
C→ Dd
C→ mi
D→ Arizona
que tiene un bucle recursivo izquierdo que involucra A B C D. Para reemplazar este bucle con recursividad directa hacia la izquierda, ordenamos los no terminales de la siguiente manera: S, A, B, C, D.
Consideremos todas las reglas generadoras de la forma
Xi→ Xj γ,
Dónde Xi Y xj son no terminales, y γ – una cadena de caracteres terminales y no terminales. En cuanto a las reglas por las cuales j ≥ yo, no se toma ninguna medida. Sin embargo, esta desigualdad no puede ser válida para todas las reglas si existe un ciclo recursivo por la izquierda. Con el orden que hemos elegido, estamos ante una única regla:
D→ Arizona
porque A precedido D en este ordenamiento. Ahora comencemos a reemplazar A, usando todas las reglas que tienen A En el lado izquierdo. Como resultado obtenemos
D→ Bbz
Porque el B precedido D al ordenar se repite el proceso, dando la regla:
D→ CCbz
Luego se repite nuevamente y da dos reglas:
D→ ecbz
D→ Ddcbz
La gramática convertida ahora se ve así:
S→ Automóvil club británico
A→ Cama y desayuno
B→ cc
C→ Dd
C→ mi
D→ Ddcbz
D→ ecbz
Todas estas reglas generadoras tienen la forma requerida y el bucle recursivo izquierdo se reemplaza por recursividad directa izquierda. Para eliminar la recursividad directa hacia la izquierda, introducimos un nuevo símbolo no terminal z y cambiar las reglas
D→ ecbz
D→ Ddcbz
D→ ecbz
D→ ecbzZ
z→ dcbz
z→ dcbzZ
Tenga en cuenta que antes y después de la transformación D genera una expresión regular
(bce) (dcbz)*
Generalizando, podemos demostrar que si un no terminal A aparece en los lados izquierdos r+ s generando reglas, r de los cuales se utiliza la recursividad directa hacia la izquierda, y s– no, es decir
A→ Aα 1, A→ Aα 2,..., A→ Aα r
A→ β 1, A→ β 2,..., A→ β s
entonces estas reglas pueden ser reemplazadas por las siguientes:
Una prueba informal es que antes y después de la transformación A genera una expresión regular ( β 1 | β 2 |... | β s) ( α 1 | α 2 |... | α r)*
Cabe señalar que al eliminar la recursividad por la izquierda (o bucle recursivo por la izquierda), todavía no obtenemos una gramática LL(1), porque Para algunos no terminales, el lado izquierdo de las reglas de las gramáticas resultantes tiene lados derechos alternativos que comienzan con los mismos símbolos. Por lo tanto, después de eliminar la recursividad por la izquierda, debemos continuar convirtiendo la gramática a la forma LL(1).
17.Conversión de gramáticas a la forma LL(1). Factorización.
Factorización
En muchas situaciones, las gramáticas que no tienen la característica LL(1) se pueden convertir en gramáticas LL(1) mediante el proceso de factorización. Veamos un ejemplo de tal situación.
PAG→comenzar D; CON fin
D→ d, D
D→ d
CON→ s; CON
CON→ s
En el proceso de factorización, reemplazamos varias reglas para un no terminal en el lado izquierdo, cuyo lado derecho comienza con el mismo símbolo (cadena de caracteres) por una regla, donde en el lado derecho, al comienzo común le sigue un introducido adicionalmente. no terminal. La gramática también se complementa con reglas para un no terminal adicional, según las cuales se derivan de él varios "residuos" del lado derecho original de la regla. Para la gramática anterior, esto dará la siguiente gramática LL(1):
PAG→comenzar D; CON fin
D→ dx X)
X→ , D(según la primera regla para D gramática original para d debería D)
X→ ε (según la segunda regla para D gramática original para d nada (línea vacía))
CON→ s y(introduzca un no terminal adicional Y)
Y→ ; CON(según la primera regla para C gramática original para s sigue; C)
Y→ ε (según la segunda regla para C gramática original para s nada (línea vacía))
De manera similar, las reglas generativas
S→ aSB
S→ aSc
S→ ε
se puede convertir mediante factorización en reglas
S→ aSX
S→ ε
X→ b
X→ C
y la gramática resultante es LL(1). Sin embargo, el proceso de factorización no puede automatizarse extendiéndolo al caso general. El siguiente ejemplo muestra lo que puede suceder. Veamos las reglas.
1. PAG→ qx
2. PAG→ ry
3. q→ m²
4. q→ q
5. R→ sRn
6. R→ r
Ambos conjuntos de personajes guía para dos opciones. PAG contener s, y tratando de "soportar s fuera de paréntesis", reemplazamos q Y R en el lado derecho de las reglas 1 y 2:
PAG→ sqmx
PAG→ sRny
PAG→ qx
PAG→ ry
Estas reglas pueden ser reemplazadas por las siguientes:
PAG→ qx
PAG→ ry
PAG→ esp 1
PAG 1 → Qmx
PAG 1 → Rny
Reglas para P1 similar a las reglas originales para PAG y tener conjuntos de caracteres guía que se cruzan. Podemos transformar estas reglas de la misma manera que las reglas para PAG:
PAG 1 → sQmmx
PAG 1 → qmx
PAG 1 → Srnny
PAG 1 → rny
Factorizando obtenemos
El procedimiento de análisis recursivo de arriba hacia abajo puede causar un problema de bucle infinito.
En una gramática para operaciones aritméticas, la aplicación de la segunda regla dará lugar a un bucle en el procedimiento de análisis. Estas gramáticas se denominan recursivas por la izquierda. Una gramática se llama recursiva por la izquierda si contiene un A no terminal para el cual hay una conclusión A=>+Aa. En casos simples, la recursividad hacia la izquierda es causada por reglas de la forma
En este caso, se introduce una nueva no terminal y las reglas originales se reemplazan por las siguientes.
(si hay un A no terminal para el cual hay una conclusión A→+Aa en 1 o más pasos). La recursividad hacia la izquierda se puede evitar transformando la gramática.
Por ejemplo, productos A→Aa
Se pueden sustituir por otros equivalentes:
Para tal caso, existe un algoritmo que elimina la recursividad hacia la izquierda:
1) definimos algún orden en el conjunto de no terminales (A 1, A 2, ..., A n)
2) tomar cada no terminal si existe una producción para él que tenga en cuenta el no terminal de la izquierda y transformar la gramática:
para i:=1 an hacer
para j:=1 a i-1 hacer
si Ai → Ajγ entonces Ai→δ1γ
│ δkγ, donde
Aj → δ1│ δ2│ …│ δk
3) excluir todos los casos de recursión izquierda inmediata (regla 1)
Eso. El algoritmo ayuda a evitar bucles.
Excluyendo la recursividad por la izquierda de la gramática de expresiones aritméticas y la forma general de la regla para eliminar la recursividad por la izquierda:
Vista general de la regla para eliminar la recursividad por la izquierda.
Factorización izquierda.
Se necesitan gramáticas LL(1) para seleccionar los productos deseados para el análisis de arriba hacia abajo, de modo que no se produzcan bucles.
A veces es posible convertir la gramática a la forma LL(1) utilizando el método de factorización por la izquierda.
Por ejemplo: S→ si B entonces S
│si B entonces S si no S
Estas producciones violan la condición de las gramáticas LL(1). Esta gramática se puede convertir a la forma LL(1).
S → si B entonces S Cola
EN vista general esta transformación se puede definir así:
introducimos un nuevo no terminal B, para el cual
| β N Para B podemos aplicar la factorización por la izquierda. Este procedimiento se repite mientras la elección del producto siga siendo incierta (es decir, mientras se pueda cambiar algo en él).
Construcción del PRIMER set.
El primer conjunto para un no terminal define el conjunto de terminales desde el cual puede comenzar este no terminal.
1. Si x es un terminal, entonces primero (x) = (x). Dado que el primer carácter de una secuencia de un terminal solo puede ser el propio terminal.
2. Si la gramática contiene la regla Xà e, entonces el conjunto primero(x) incluye e. Esto significa que X puede comenzar con una secuencia vacía, es decir, estar ausente por completo.
3. Para todos los productos de la forma XàY1 Y2… Yk realizamos lo siguiente. Agregamos el conjunto primero (Yi) al conjunto primero (X) hasta que el primero (Yi-1) contenga e y el primero (Yi) no contenga e. En este caso, i cambia de 0 a k. Esto es necesario porque si puede faltar Yi-1, entonces es necesario averiguar dónde comenzará toda la secuencia en este caso.
propiedad LL(k) impone grandes restricciones a la gramática. A veces es posible transformar una gramática para que la gramática resultante tenga propiedad LL(1) . Esta transformación no siempre tiene éxito, pero si es posible obtener una gramática LL(1), entonces para construir un analizador se puede utilizar el método de descenso recursivo sin retroceder.
Supongamos que necesitamos construir un analizador para un lenguaje generado por la siguiente gramática:
mi → mi + t | mi – t | t
T → T * F | V/F | F
F → número | (mi)
Múltiples terminales PRIMERO(T) también pertenecen al conjunto PRIMERO(E+T) Por lo tanto, es imposible determinar sin ambigüedades la secuencia de llamadas a procedimientos que deben realizarse al analizar la cadena de entrada. El problema es que el no terminal mi ocurre en la primera posición del lado derecho de la regla, el lado izquierdo del cual también es mi. En tal situación, el no terminal mi se llama recursivo directamente a la izquierda.
No terminal A Gramáticas KS GRAMO llamado recursivo izquierdo , si hay una conclusión en la gramática A =>* ay.
Una gramática que tiene al menos una regla recursiva por la izquierda no puede ser LL(1)-gramática.
Por otro lado, se sabe que cada lenguaje CS está definido por al menos una gramática recursiva no izquierda.
Algoritmo para eliminar la recursividad por la izquierda.
Dejar GRAMO = (norte, T, P, S)– KS-gramática y regla A → Aw 1 | ay 2 | ... | ay norte | v 1 | v 2 | ... | v metro representa todas las reglas de PAG que contiene A en el lado izquierdo, y ninguna de las cadenas v i no comienza con un no terminal A.
Agreguemos al conjunto norte otro no terminal A" y reemplazar las reglas que contienen A en el lado izquierdo, a lo siguiente:
A → v 1 | v 2 | ... | v metro | v 1 A' | v 2 A' | ... | v metro A"
A' → w 1 | w 2 | ... | w norte | w 1 A' | w 2 A' | ...| w norte A"
Se puede demostrar que la gramática resultante es equivalente a la original.
Como resultado de aplicar esta transformación a la gramática anterior que describe expresiones aritméticas, obtenemos la siguiente gramática:
mi → t | T.E."
mi" → + t | + T.E."
t → F | PIE."
t"→ * F | * PIE."
F → (mi) | número
Es fácil demostrar que la gramática resultante tiene la propiedad LL(1).
Otro problema similar ocurre cuando dos reglas para el mismo no terminal comienzan con los mismos caracteres.
Por ejemplo,
S → si E entonces S si no S
S → si mi entonces S
En este caso agregaremos otro no terminal que corresponderá a las diferentes terminaciones de estas reglas. Obtenemos las siguientes reglas:
S → si mi entonces S S’
S" →
S"→ demás S
Para la gramática resultante, se puede implementar el método de descenso recursivo.
9.1.4. Descenso recursivo con retornos.
Para poder aplicar el método de descenso recursivo es necesario 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 transforma la gramática a una forma en la que conjuntos PRIMERO no se cruzan, lo cual es un proceso complejo, por lo que en la práctica se utiliza una técnica llamada descenso recursivo con retornos .
Para ello, el analizador léxico se representa como un objeto que, además de los métodos tradicionales escanear, próximo etc., también hay un constructor de copias. Luego, en todas las situaciones en las que pueda surgir ambigüedad, antes de comenzar a analizar, es necesario recordar el estado actual del analizador léxico (es decir, hacer una copia del analizador léxico) y continuar analizando el texto, considerando que estamos ante el primero de las posibles construcciones en esta situación. Si esta opción de análisis falla, entonces deberá restaurar el estado del analizador léxico e intentar analizar el mismo fragmento nuevamente usando siguiente opción gramática, etc. Si todas las opciones de análisis fallan, se informa un error.
Este método de análisis es potencialmente más lento que el descenso recursivo sin retroceso, pero en este caso logra mantener la gramática en su forma original y ahorrar esfuerzo al programador.