Возведение в степень предполагает, что данное число необходимо умножить само на себя определенное количество раз. Например, возведение числа 2 в пятую степень будет выглядеть следующим образом:
Число, которое нужно умножать само на себя, называется основанием степени, а количество умножений – ее показателем. Возведению в степень соответствуют два противоположных действия: нахождение показателя и нахождение основания.
Извлечение корня
Нахождение основание степени называется извлечением корня. Это означает, что необходимо найти число, которое нужно возвести в степень n, чтобы получить данное.
Например, необходимо извлечь корень 4-й степени из числа 16, т.е. определить, нужно умножить само на себя 4 раза, чтобы в итоге получить 16. Это число – 2.
Такое арифметическое действие записывается с помощью особого знака – радикала: √, над которым слева указывается показатель степени.
Арифметический корень
Если показатель степени является четный числом, то корнем могут оказаться два числа с одинаковым модулем, но с – положительное и отрицательное. Так, в приведенном примере это могут быть числа 2 и -2.
Выражение должно быть однозначным, т.е. иметь один результат. Для этого и было введено понятие арифметического корня, который может представлять собой только положительное число. Быть меньше нуля арифметический корень не может.
Таким образом, в рассмотренном выше примере арифметическим корнем будет только число 2, а второй вариант ответа – -2 – исключается по определению.
Квадратный корень
Для некоторых степеней, которые используются чаще других, в существуют специальные названия, которые изначально связаны с геометрией. Речь идет о возведении во вторую и третью степени.
Во вторую степень длину стороны квадрата, когда нужно вычислить его площадь. Если же нужно найти объем куба, длину его ребра возводят в третью степень. Поэтому называется квадратом числа, а третья – кубом.
Соответственно, корень второй степени называется квадратным, а корень третьей степени – кубическим. Квадратный корень – единственный из корней, при записи которого над радикалом не ставится показатель степени:
Итак, арифметический квадратный корень из данного числа – это положительное число, которое необходимо возвести во вторую степень, чтобы получить данное число.
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
Рациональные числа
Неотрицательный квадратный корень из положительного числа называется арифметическим квадратным корнем и обозначается с использованием знака радикала .
Комплексные числа
Над полем комплексных чисел решений всегда два, отличающихся толькознаком (за исключением квадратного корня из нуля). Корень изкомплексного числа часто обозначают как , однако использовать это обозначение нужно осторожно. Распространённая ошибка:
Для извлечения квадратного корня из комплексного числа удобноиспользовать экспоненциальную форму записи комплексного числа: если
, ![]() ,
,
где корень из модуля понимается в смысле арифметического значения, а k может принимать значения k=0 и k=1, таким образом в итоге в ответеполучаются два различных результата.
Обобщения
Квадратные корни вводятся как решения уравнений вида и для других объектов: матриц , функций , операторов и т. п. В качестве операции при этом могут использоваться достаточно произвольные мультипликативные операции, например, суперпозиция .
Квадратный корень в информатике
Во многих языках программирования функционального уровня (а также языках разметки типа LaTeX) функция квадратного корня обозначается как sqrt (от англ. square root «квадратный корень»).
Алгоритмы нахождения квадратного корня
Нахождение или вычисление квадратного корня заданного числа называется извлечением (квадратного) корня.
Разложение в ряд Тейлора
при .
Арифметическое извлечение квадратного корня
Для квадратов чисел верны следующие равенства:
![]()
![]()
То есть, узнать целую часть квадратного корня числа можно, вычитая из него все нечётные числа попорядку, пока остаток не станет меньше следующего вычитаемого числа илиравен нулю, и посчитав количество выполненных действий. Например, так:
Выполнено 3 действия, квадратный корень числа 9 равен 3.
Недостатком такого способа является то, что если извлекаемый кореньне является целым числом, то можно узнать только его целую часть, но неточнее. В то же время такой способ вполне доступен детям, решающимпростейшие математические задачи, требующие извлечения квадратногокорня.
Грубая оценка
Многие алгоритмы вычисления квадратных корней из положительного действительного числа S требуют некоторого начального значения. Если начальное значение слишком далеко от настоящего значения корня, вычисления замедляются. Поэтомуполезно иметь грубую оценку, которая может быть очень неточна, но легковычисляется. Если S ≥ 1, пусть D будет числом цифр S слева от десятичной запятой. Если S D будет числом нулей, идущих подряд, справа от десятичной запятой, взятое со знаком минус. Тогда грубая оценка выглядит так:
Если D нечётно, D = 2n + 1, тогда используем ![]() Если D чётно, D = 2n + 2, тогда используем
Если D чётно, D = 2n + 2, тогда используем ![]()
Два и шесть используются потому, что ![]() и
и
При работе в двоичной системе (как внутри компьютеров), следует использовать другую оценку (здесь D это число двоичных цифр).
Геометрическое извлечение квадратного корня
Для ручного извлечения корня применяется запись, похожая на деление столбиком . Выписывается число, корень которого ищем. Справа от него будемпостепенно получать цифры искомого корня. Пусть извлекается корень изчисла с конечным числом знаков после запятой. Для начала мысленно или метками разобьём число N на группы по две цифры слева и справа от десятичнойточки. При необходимости, группы дополняются нулями — целая частьдополняется слева, дробная справа. Так 31234.567 можно представить, как03 12 34 . 56 70. В отличие от деления снос производится такими группами по 2 цифры.
Наглядное описание алгоритма:
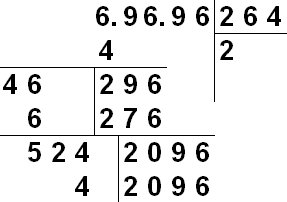
Факт 1.(bullet) Возьмем некоторое неотрицательное число (a) (то есть (ageqslant 0)). Тогда (арифметическим) квадратным корнем из числа (a) называется такое неотрицательное число (b), при возведении которого в квадрат мы получим число (a): [sqrt a=bquad text{то же самое, что }quad a=b^2] Из определения следует, что (ageqslant 0, bgeqslant 0). Эти ограничения являются важным условием существования квадратного корня и их следует запомнить!Вспомним, что любое число при возведении в квадрат дает неотрицательный результат. То есть (100^2=10000geqslant 0) и ((-100)^2=10000geqslant 0).(bullet) Чему равен (sqrt{25})? Мы знаем, что (5^2=25) и ((-5)^2=25). Так как по определению мы должны найти неотрицательное число, то (-5) не подходит, следовательно, (sqrt{25}=5) (так как (25=5^2)).Нахождение значения (sqrt a) называется извлечением квадратного корня из числа (a), а число (a) называется подкоренным выражением.(bullet) Исходя из определения, выражения (sqrt{-25}), (sqrt{-4}) и т.п. не имеют смысла.
Факт 2.Для быстрых вычислений полезно будет выучить таблицу квадратов натуральных чисел от (1) до (20): [begin{array}{|ll|}hline1^2=1 & quad11^2=121 \2^2=4 & quad12^2=144\3^2=9 & quad13^2=169\4^2=16 & quad14^2=196\5^2=25 & quad15^2=225\6^2=36 & quad16^2=256\7^2=49 & quad17^2=289\8^2=64 & quad18^2=324\9^2=81 & quad19^2=361\10^2=100& quad20^2=400\hline end{array}]
Факт 3.Какие действия можно выполнять с квадратными корнями?(bullet) Сумма или разность квадратных корней НЕ РАВНА квадратному корню из суммы или разности, то есть [sqrt apmsqrt bne sqrt{apm b}] Таким образом, если вам нужно вычислить, например, (sqrt{25}+sqrt{49}), то первоначально вы должны найти значения (sqrt{25}) и (sqrt{49}), а затем их сложить. Следовательно, [sqrt{25}+sqrt{49}=5+7=12] Если значения (sqrt a) или (sqrt b) при сложении (sqrta+sqrt b) найти не удается, то такое выражение дальше не преобразуется и остается таким, как есть. Например, в сумме (sqrt2+ sqrt {49}) мы можем найти (sqrt{49}) – это (7), а вот (sqrt2) никак преобразовать нельзя, поэтому (sqrt 2+sqrt{49}=sqrt2+7). Дальше это выражение, к сожалению, упростить никак нельзя (bullet) Произведение/частное квадратных корней равно квадратному корню из произведения/частного, то есть [sqrt acdot sqrt b=sqrt{ab}quad text{и}quadsqrt a:sqrt b=sqrt{a:b}] (при условии, что обе части равенств имеют смысл)Пример: (sqrt{32}cdot sqrt 2=sqrt{32cdot2}=sqrt{64}=8); (sqrt{768}:sqrt3=sqrt{768:3}=sqrt{256}=16); (sqrt{(-25)cdot (-64)}=sqrt{25cdot 64}=sqrt{25}cdot sqrt{64}=5cdot 8=40). (bullet) Пользуясь этими свойствами, удобно находить квадратные корни из больших чисел путем разложения их на множители.Рассмотрим пример. Найдем (sqrt{44100}). Так как (44100:100=441), то (44100=100cdot 441). По признаку делимости число (441) делится на (9) (так как сумма его цифр равна 9 и делится на 9), следовательно, (441:9=49), то есть (441=9cdot 49).Таким образом, мы получили: [sqrt{44100}=sqrt{9cdot 49cdot 100}=sqrt9cdot sqrt{49}cdot sqrt{100}=3cdot 7cdot 10=210] Рассмотрим еще один пример: [sqrt{dfrac{32cdot 294}{27}}=sqrt{dfrac{16cdot 2cdot 3cdot 49cdot 2}{9cdot 3}}= sqrt{dfrac{16cdot4cdot49}{9}}=dfrac{sqrt{16}cdot sqrt4 cdotsqrt{49}}{sqrt9}=dfrac{4cdot 2cdot 7}3=dfrac{56}3](bullet) Покажем, как вносить числа под знак квадратного корня на примере выражения (5sqrt2) (сокращенная запись от выражения (5cdotsqrt2)). Так как (5=sqrt{25}), то Заметим также, что, например,1) (sqrt2+3sqrt2=4sqrt2),2) (5sqrt3-sqrt3=4sqrt3)3) (sqrt a+sqrt a=2sqrt a).
Почему так? Объясним на примере 1). Как вы уже поняли, как-то преобразовать число (sqrt2) мы не можем. Представим, что (sqrt2) – это некоторое число (a). Соответственно, выражение (sqrt2+3sqrt2) есть не что иное, как (a+3a) (одно число (a) плюс еще три таких же числа (a)). А мы знаем, что это равно четырем таким числам (a), то есть (4sqrt2).
Факт 4.(bullet) Часто говорят “нельзя извлечь корень”, когда не удается избавиться от знака (sqrt {} ) корня (радикала) при нахождении значения какого-то числа. Например, извлечь корень из числа (16) можно, потому что (16=4^2), поэтому (sqrt{16}=4). А вот извлечь корень из числа (3), то есть найти (sqrt3), нельзя, потому что нет такого числа, которое в квадрате даст (3).Такие числа (или выражения с такими числами) являются иррациональными. Например, числа (sqrt3, 1+sqrt2, sqrt{15}) и т.п. являются иррациональными.Также иррациональными являются числа (pi) (число “пи”, приблизительно равное (3,14)), (e) (это число называют числом Эйлера, приблизительно оно равно (2,7)) и т.д.(bullet) Обращаем ваше внимание на то, что любое число будет либо рациональным, либо иррациональным. А вместе все рациональные и все иррациональные числа образуют множество, называющееся множеством действительных (вещественных) чисел. Обозначается это множество буквой (mathbb{R}).Значит, все числа, которые на данный момент мы знаем, называются вещественными числами.
Факт 5.(bullet) Модуль вещественного числа (a) – это неотрицательное число (|a|), равное расстоянию от точки (a) до (0) на вещественной прямой. Например, (|3|) и (|-3|) равны 3, так как расстояния от точек (3) и (-3) до (0) одинаковы и равны (3). (bullet) Если (a) – неотрицательное число, то (|a|=a).Пример: (|5|=5); (qquad |sqrt2|=sqrt2). (bullet) Если (a) – отрицательное число, то (|a|=-a).Пример: (|-5|=-(-5)=5); (qquad |-sqrt3|=-(-sqrt3)=sqrt3).Говорят, что у отрицательных чисел модуль “съедает” минус, а положительные числа, а также число (0), модуль оставляет без изменений.НО такое правило годится только для чисел. Если у вас под знаком модуля находится неизвестная (x) (или какая-то другая неизвестная), например, (|x|), про которую мы не знаем, положительная она, равна нулю или отрицательная, то избавиться от модуля мы не можем. В этом случае это выражение таким и остается: (|x|). (bullet) Имеют место следующие формулы: [{large{sqrt{a^2}=|a|}}] [{large{(sqrt{a})^2=a}},text{ при условии } ageqslant 0] Очень часто допускается такая ошибка: говорят, что (sqrt{a^2}) и ((sqrt a)^2) – одно и то же. Это верно только в том случае, когда (a) – положительное число или ноль. А вот если (a) – отрицательное число, то это неверно. Достаточно рассмотреть такой пример. Возьмем вместо (a) число (-1). Тогда (sqrt{(-1)^2}=sqrt{1}=1), а вот выражение ((sqrt {-1})^2) вообще не существует (ведь нельзя под знак корня помещать отрицательные числа!).Поэтому обращаем ваше внимание на то, что (sqrt{a^2}) не равен ((sqrt a)^2)! Пример: 1) (sqrt{left(-sqrt2right)^2}=|-sqrt2|=sqrt2), т.к. (-sqrt2
(phantom{00000}) 2) ((sqrt{2})^2=2). (bullet) Так как (sqrt{a^2}=|a|), то [sqrt{a^{2n}}=|a^n|] (выражение (2n) обозначает четное число)То есть при извлечении корня из числа, находящегося в какой-то степени, эта степень уменьшается в два раза.Пример:1) (sqrt{4^6}=|4^3|=4^3=64)2) (sqrt{(-25)^2}=|-25|=25) (заметим, что если модуль не поставить, то получится, что корень из числа равен (-25); но мы помним, что по определению корня такого быть не может: у нас всегда при извлечении корня должно получаться положительное число или ноль)3) (sqrt{x^{16}}=|x^8|=x^8) (так как любое число в четной степени неотрицательно)
Факт 6.Как сравнить два квадратных корня?(bullet) Для квадратных корней верно: если (sqrt aПример:1) сравним (sqrt{50}) и (6sqrt2). Для начала преобразуем второе выражение в (sqrt{36}cdot sqrt2=sqrt{36cdot 2}=sqrt{72}). Таким образом, так как (502) Между какими целыми числами находится (sqrt{50})?Так как (sqrt{49}=7), (sqrt{64}=8), а (493) Сравним (sqrt 2-1) и (0,5). Предположим, что (sqrt2-1>0,5): [begin{aligned}&sqrt 2-1>0,5 big| +1quad text{(прибавим единицу к обеимчастям)}\&sqrt2>0,5+1 big| ^2 quadtext{(возведем обе части вквадрат)}\&2>1,5^2\&2>2,25 end{aligned}] Видим, что мы получили неверное неравенство. Следовательно, наше предположение было неверным и (sqrt 2-1Заметим, что прибавление некоторого числа к обеим частям неравенства не влияет на его знак. Умножение/деление обеих частей неравенства на положительное число также не влияет на его знак, а умножение/деление на отрицательное число меняет знак неравенства на противоположный!Возводить обе части уравнения/неравенства в квадрат можно ТОЛЬКО ТОГДА, когда обе части неотрицательные. Например, в неравенстве из предыдущего примера возводить обе части в квадрат можно, в неравенстве (-3 (bullet) Следует запомнить, что [begin{aligned}&sqrt 2approx 1,4\&sqrt 3approx 1,7 end{aligned}] Знание приблизительного значения данных чисел поможет вам при сравнении чисел! (bullet) Для того, чтобы извлечь корень (если он извлекается) из какого-то большого числа, которого нет в таблице квадратов, нужно сначала определить, между какими “сотнями” оно находится, затем – между какими “десятками”, а потом уже определить последнюю цифру этого числа. Покажем, как это работает, на примере.Возьмем (sqrt{28224}). Мы знаем, что (100^2=10,000), (200^2=40,000) и т.д. Заметим, что (28224) находится между (10,000) и (40,000). Следовательно, (sqrt{28224}) находится между (100) и (200).Теперь определим, между какими “десятками” находится наше число (то есть, например, между (120) и (130)). Также из таблицы квадратов знаем, что (11^2=121), (12^2=144) и т.д., тогда (110^2=12100), (120^2=14400), (130^2=16900), (140^2=19600), (150^2=22500), (160^2=25600), (170^2=28900). Таким образом, мы видим, что (28224) находится между (160^2) и (170^2). Следовательно, число (sqrt{28224}) находится между (160) и (170).Попробуем определить последнюю цифру. Давайте вспомним, какие однозначные числа при возведении в квадрат дают на конце (4)? Это (2^2) и (8^2). Следовательно, (sqrt{28224}) будет заканчиваться либо на 2, либо на 8. Проверим это. Найдем (162^2) и (168^2):(162^2=162cdot 162=26224)(168^2=168cdot 168=28224).Следовательно, (sqrt{28224}=168). Вуаля!
Для того чтобы достойно решить ЕГЭ по математике, прежде всего необходимо изучить теоретический материал, который знакомит с многочисленными теоремами, формулами, алгоритмами и т. д. На первый взгляд может показаться, что это довольно просто. Однако найти источник, в котором теория для ЕГЭ по математике изложена легко и понятно для учащихся с любым уровнем подготовки, — на деле задача довольно сложная. Школьные учебники невозможно всегда держать под рукой. А найти основные формулы для ЕГЭ по математике бывает непросто даже в Интернете.
Почему так важно изучать теорию по математике не только для тех, кто сдает ЕГЭ?
- Потому что это расширяет кругозор. Изучение теоретического материала по математике полезно для всех, кто желает получить ответы на широкий круг вопросов, связанных с познанием окружающего мира. Все в природе упорядоченно и имеет четкую логику. Именно это и отражается в науке, через которую возможно понять мир.
- Потому что это развивает интеллект. Изучая справочные материалы для ЕГЭ по математике, а также решая разнообразные задачи, человек учится логически мыслить и рассуждать, грамотно и четко формулировать мысли. У него вырабатывается способность анализировать, обобщать, делать выводы.
Предлагаем вам лично оценить все преимущества нашего подхода к систематизации и изложению учебных материалов.

