Fonctions trigonométriques

Cet article contient tables de sinus, cosinus, tangentes et cotangentes. Nous fournirons d’abord un tableau de valeurs de base fonctions trigonométriques, c'est-à-dire une table de sinus, cosinus, tangentes et cotangentes des angles 0, 30, 45, 60, 90, ..., 360 degrés ( 0, π/6, π/4, π/3, π/2, …, 2π radian). Après cela, nous donnerons un tableau des sinus et des cosinus, ainsi qu'un tableau des tangentes et cotangentes de V. M. Bradis, et montrerons comment utiliser ces tableaux pour trouver les valeurs des fonctions trigonométriques.

Navigation dans les pages.

Tableau des sinus, cosinus, tangentes et cotangentes pour des angles de 0, 30, 45, 60, 90, ... degrés

Bibliographie.

• Algèbre: Cahier de texte pour la 9ème année. moy. école/Yu. N. Makarychev, N. G. Mindyuk, K. I. Neshkov, S. B. Suvorova ; Éd. S. A. Telyakovsky - M. : Éducation, 1990. - 272 pp. : ill. - ISBN 5-09-002727-7.
• Bashmakov M.I. Algèbre et débuts de l'analyse : Manuel. pour les classes 10-11. moy. école - 3e éd. - M. : Éducation, 1993. - 351 p. : ill. - ISBN5-09-004617-4.
• Algèbre et le début de l'analyse : Proc. pour les classes 10-11. enseignement général institutions / A. N. Kolmogorov, A. M. Abramov, Yu. P. Dudnitsyn et autres ; Éd. A. N. Kolmogorov - 14e éd. - M. : Éducation, 2004. - 384 pp. : ill.
• Gusev V.A., Mordkovitch A.G. Mathématiques (un manuel pour ceux qui entrent dans les écoles techniques) : Proc. allocation.- M.; Plus haut école, 1984.-351 p., ill.
• Bradis V. M. Tableaux mathématiques à quatre chiffres : Pour l'enseignement général. cahier de texte établissements. - 2e éd. - M. : Outarde, 1999.- 96 p. : ill. ISBN5-7107-2667-2

Nous commencerons notre étude de la trigonométrie par le triangle rectangle. Définissons ce que sont le sinus et le cosinus, ainsi que la tangente et la cotangente d'un angle aigu. Ce sont les bases de la trigonométrie.

Rappelons que angle droit est un angle égal à 90 degrés. En d’autres termes, un demi-angle tourné.

Angle vif- moins de 90 degrés.

Angle obtus- supérieur à 90 degrés. Par rapport à un tel angle, « obtus » n'est pas une insulte, mais un terme mathématique :-)

Traçons un triangle rectangle. Un angle droit est généralement noté . Veuillez noter que le côté opposé au coin est indiqué par la même lettre, seulement en petite. Ainsi, le côté opposé à l'angle A est désigné .

L'angle est indiqué par la lettre grecque correspondante.

Hypoténuse d'un triangle rectangle est le côté opposé à l'angle droit.

Jambes- les côtés opposés aux angles aigus.

La jambe située à l'opposé de l'angle s'appelle opposé(par rapport à l'angle). L'autre jambe, qui se trouve sur l'un des côtés de l'angle, s'appelle adjacent.

Sinus L'angle aigu dans un triangle rectangle est le rapport du côté opposé à l'hypoténuse :

Cosinus angle aigu dans un triangle rectangle - le rapport de la jambe adjacente à l'hypoténuse :

Tangente angle aigu dans un triangle rectangle - le rapport du côté opposé au côté adjacent :

Autre définition (équivalente) : la tangente d'un angle aigu est le rapport du sinus de l'angle à son cosinus :

Cotangente angle aigu dans un triangle rectangle - le rapport du côté adjacent au côté opposé (ou, ce qui revient au même, le rapport du cosinus au sinus) :

Notez les relations de base pour le sinus, le cosinus, la tangente et la cotangente ci-dessous. Ils nous seront utiles pour résoudre des problèmes.

Prouvons-en quelques-uns.

D'accord, nous avons donné des définitions et des formules écrites. Mais pourquoi avons-nous encore besoin de sinus, cosinus, tangente et cotangente ?

Nous savons que la somme des angles de tout triangle est égale à.

Nous connaissons la relation entre des soirées triangle rectangle. C'est le théorème de Pythagore : .

Il s'avère qu'en connaissant deux angles dans un triangle, vous pouvez trouver le troisième. Connaissant les deux côtés d’un triangle rectangle, vous pouvez trouver le troisième. Cela signifie que les angles ont leur propre rapport et que les côtés ont le leur. Mais que faire si dans un triangle rectangle vous connaissez un angle (sauf l'angle droit) et un côté, mais que vous devez trouver les autres côtés ?

C’est ce que les gens rencontraient autrefois lorsqu’ils dressaient des cartes de la région et du ciel étoilé. Après tout, il n’est pas toujours possible de mesurer directement tous les côtés d’un triangle.

Sinus, cosinus et tangente - on les appelle aussi fonctions d'angle trigonométrique- donner des relations entre des soirées Et coins Triangle. Connaissant l'angle, vous pouvez retrouver toutes ses fonctions trigonométriques à l'aide de tableaux spéciaux. Et connaissant les sinus, cosinus et tangentes des angles d’un triangle et d’un de ses côtés, vous pouvez trouver le reste.

Nous dresserons également un tableau des valeurs du sinus, du cosinus, de la tangente et de la cotangente pour les « bons » angles de à.

Veuillez noter les deux tirets rouges dans le tableau. Aux valeurs d'angle appropriées, la tangente et la cotangente n'existent pas.

Examinons plusieurs problèmes de trigonométrie de la banque de tâches FIPI.

1. Dans un triangle, l’angle est , . Trouver .

Le problème est résolu en quatre secondes.

Parce que le , .

2. Dans un triangle, l'angle est , , . Trouver .

Trouvons-le en utilisant le théorème de Pythagore.

Le problème est résolu.

Souvent, dans les problèmes, il y a des triangles avec des angles et ou avec des angles et. Retenez par cœur les ratios de base pour eux !

Pour un triangle avec des angles et la branche opposée à l'angle en est égale à la moitié de l'hypoténuse.

Un triangle avec des angles et est isocèle. Dans celui-ci, l'hypoténuse est plusieurs fois plus grande que la jambe.

Nous avons examiné des problèmes pour résoudre des triangles rectangles, c'est-à-dire trouver des côtés ou des angles inconnus. Mais ce n'est pas tout! DANS Options d'examen d'État unifié en mathématiques, il existe de nombreux problèmes dans lesquels apparaît le sinus, le cosinus, la tangente ou la cotangente de l'angle externe d'un triangle. Plus d’informations à ce sujet dans le prochain article.

Dans l'article, nous comprendrons parfaitement à quoi cela ressemble tableau des valeurs trigonométriques, sinus, cosinus, tangente et cotangente. Considérons la signification fondamentale des fonctions trigonométriques, sous un angle de 0,30,45,60,90,...,360 degrés. Et voyons comment utiliser ces tableaux pour calculer les valeurs des fonctions trigonométriques.
Regardons d'abord table de cosinus, sinus, tangente et cotangente sous un angle de 0, 30, 45, 60, 90,... degrés. La définition de ces grandeurs permet de déterminer la valeur des fonctions des angles de 0 et 90 degrés :

sin 0 0 =0, cos 0 0 = 1. tg 00 = 0, la cotangente de 00 sera indéfinie
sin 90 0 = 1, cos 90 0 =0, ctg90 0 = 0, la tangente à partir de 90 0 sera incertaine

Si vous prenez des triangles rectangles dont les angles sont de 30 à 90 degrés. On a:

sin 30 0 = 1/2, cos 30 0 = √3/2, tan 30 0 = √3/3, cos 30 0 = √3
sin 45 0 = √2/2, cos 45 0 = √2/2, tan 45 0 = 1, cos 45 0 = 1
sin 60 0 = √3/2, cos 60 0 = 1/2, tg 60 0 =√3, lit bébé 60 0 = √3/3

Représentons toutes les valeurs obtenues sous la forme table trigonométrique:

Tableau des sinus, cosinus, tangentes et cotangentes !

Si nous utilisons la formule de réduction, notre tableau augmentera en ajoutant des valeurs pour des angles jusqu'à 360 degrés. Cela ressemblera à :

De plus, en fonction des propriétés de périodicité, le tableau peut être augmenté si nous remplaçons les angles par 0 0 +360 0 *z .... 330 0 +360 0 *z, dans lequel z est un nombre entier. Dans ce tableau, il est possible de calculer la valeur de tous les angles correspondant aux points d'un même cercle.

Voyons comment utiliser le tableau dans une solution.
Tout est très simple. Puisque la valeur dont nous avons besoin se situe au point d’intersection des cellules dont nous avons besoin. Par exemple, prenons le cosinus d'un angle de 60 degrés, dans le tableau cela ressemblera à :

Dans le tableau final des principales valeurs des fonctions trigonométriques, on procède de la même manière. Mais dans ce tableau, il est possible de savoir quelle est la tangente d'un angle de 1020 degrés, elle = -√3 Vérifions 1020 0 = 300 0 +360 0 *2. Trouvons-le à l'aide du tableau.

Table Bradis. Pour sinus, cosinus, tangente et cotangente.

Les tables de Bradis sont divisées en plusieurs parties, constituées de tables de cosinus et de sinus, de tangente et de cotangente - qui sont divisées en deux parties (tg des angles jusqu'à 90 degrés et ctg des petits angles).

Sinus et cosinus

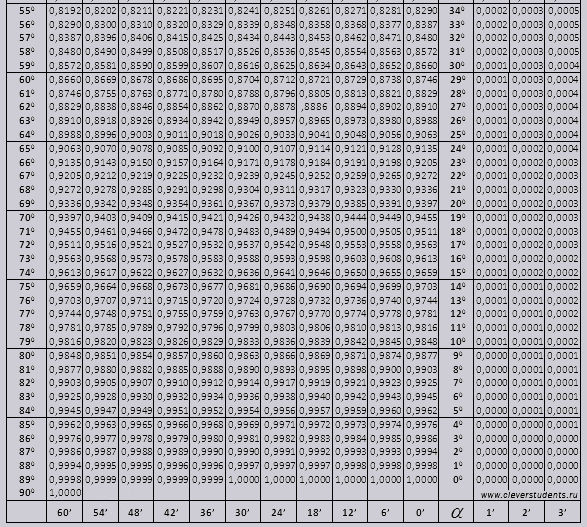
tg d'angle commençant par 00 se terminant par 760, ctg d'angle commençant par 140 se terminant par 900.

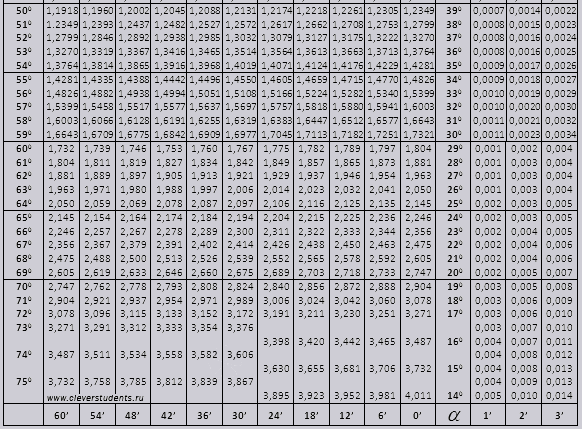
tg jusqu'à 900 et ctg des petits angles.

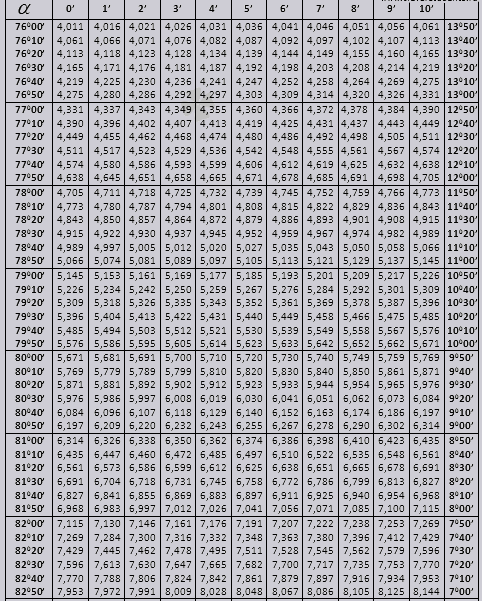
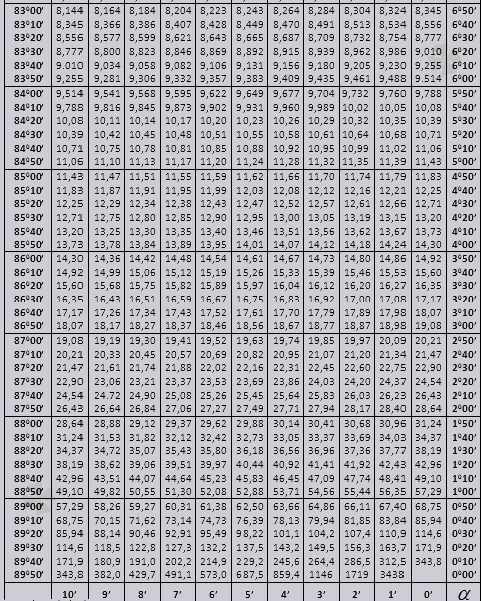
Voyons comment utiliser les tables de Bradis pour résoudre des problèmes.

Trouvons la désignation sin (désignation dans la colonne du bord gauche) 42 minutes (la désignation est sur la ligne du haut). Par intersection on cherche la désignation, elle = 0,3040.

Les valeurs des minutes sont indiquées avec un intervalle de six minutes, que faire si la valeur dont nous avons besoin se situe exactement dans cet intervalle. Prenons 44 minutes, mais il n'y en a que 42 dans le tableau. On prend 42 comme base et on utilise les colonnes supplémentaires du côté droit, on prend le 2ème amendement et on ajoute à 0,3040 + 0,0006 on obtient 0,3046.

Avec sin 47 minutes, on prend 48 minutes comme base et on en soustrait 1 correction, soit 0,3057 - 0,0003 = 0,3054

Lors du calcul du cos, nous travaillons de la même manière que le péché, sauf que nous prenons comme base la ligne du bas du tableau. Par exemple cos 20 0 = 0,9397

Les valeurs de l'angle tg jusqu'à 90 0 et du cot d'un petit angle sont correctes et ne contiennent aucune correction. Par exemple, trouvez tg 78 0 37min = 4,967


et ctg 20 0 13min = 25,83

Eh bien, nous avons examiné les tables trigonométriques de base. Nous espérons que ces informations vous ont été extrêmement utiles. Si vous avez des questions sur les tableaux, n'hésitez pas à les écrire dans les commentaires !

Remarque : Les pare-chocs muraux sont des panneaux pare-chocs destinés à protéger les murs. Suivez le lien sur les pare-chocs muraux sans cadre (http://www.spi-polymer.ru/otboyniki/) et découvrez-en plus.

Tableau des fonctions trigonométriques de base pour les angles de 0, 30, 45, 60, 90, ... degrés

A partir des définitions trigonométriques des fonctions $\sin$, $\cos$, $\tan$ et $\cot$, vous pouvez connaître leurs valeurs pour les angles $0$ et $90$ degrés :

$\sin⁡0°=0$, $\cos0°=1$, $\tan 0°=0$, $\cot 0°$ non défini ;

$\sin90°=1$, $\cos90°=0$, $\cot90°=0$, $\tan 90°$ n'est pas défini.

DANS cours scolaire En géométrie, lorsqu'on étudie les triangles rectangles, on retrouve les fonctions trigonométriques des angles $0°$, $30°$, $45°$, $60°$ et $90°$.

Valeurs trouvées des fonctions trigonométriques pour les angles indiqués en degrés et en radians, respectivement ($0$, $\frac(\pi)(6)$, $\frac(\pi)(4)$, $\frac(\ pi)(3) $, $\frac(\pi)(2)$) pour faciliter la mémorisation et l'utilisation sont saisis dans un tableau appelé table trigonométrique, tableau des valeurs de base des fonctions trigonométriques et ainsi de suite.

Lors de l'utilisation de formules de réduction, la table trigonométrique peut être étendue à un angle de $360°$ et, par conséquent, $2\pi$ radians :

En utilisant les propriétés de périodicité des fonctions trigonométriques, chaque angle, qui différera de celui déjà connu de $360°$, peut être calculé et enregistré dans un tableau. Par exemple, la fonction trigonométrique pour l'angle $0°$ aura la même valeur pour l'angle $0°+360°$, et pour l'angle $0°+2 \cdot 360°$, et pour l'angle $0°+3 \cdot 360°$ et etc.

À l'aide d'un tableau trigonométrique, vous pouvez déterminer les valeurs de tous les angles d'un cercle unité.

Dans un cours de géométrie scolaire, vous êtes censé mémoriser les valeurs de base des fonctions trigonométriques rassemblées dans un tableau trigonométrique pour faciliter la résolution de problèmes trigonométriques.

Utiliser un tableau

Dans le tableau, il suffit de trouver la fonction trigonométrique recherchée et la valeur de l'angle ou des radians pour lesquels cette fonction doit être calculée. A l'intersection de la ligne avec la fonction et de la colonne avec la valeur, on obtient la valeur souhaitée de la fonction trigonométrique de l'argument donné.

Dans la figure, vous pouvez voir comment trouver la valeur de $\cos⁡60°$, qui est égale à $\frac(1)(2)$.

Le tableau trigonométrique étendu s'utilise de la même manière. L'avantage de son utilisation réside, comme déjà mentionné, dans le calcul de la fonction trigonométrique de presque tous les angles. Par exemple, vous pouvez facilement trouver la valeur $\tan 1 380°=\tan (1 380°-360°)=\tan(1 020°-360°)=\tan(660°-360°)=\tan300 °$ :

Tableaux de Bradis des fonctions trigonométriques de base

La possibilité de calculer la fonction trigonométrique d'absolument n'importe quelle valeur d'angle pour une valeur entière de degrés et une valeur entière de minutes est assurée par l'utilisation des tables de Bradis. Par exemple, trouvez la valeur de $\cos⁡34°7"$. Les tableaux sont divisés en 2 parties : un tableau des valeurs de $\sin$ et $\cos$ et un tableau des valeurs de $ \tan$ et $\cot$.

Les tables de Bradis permettent d'obtenir des valeurs approximatives des fonctions trigonométriques avec une précision jusqu'à 4 décimales.

Utiliser les tables Bradis

En utilisant les tables de Bradis pour les sinus, on trouve $\sin⁡17°42"$. Pour ce faire, dans la colonne de gauche du tableau des sinus et cosinus on trouve la valeur des degrés - $17°$, et dans la ligne du haut nous trouvons la valeur des minutes - $42"$. A leur intersection on obtient la valeur souhaitée :

$\sin17°42"=0,304$.

Pour trouver la valeur $\sin17°44"$ vous devez utiliser la correction située à droite du tableau. dans ce casà la valeur $42"$ qui se trouve dans le tableau, vous devez ajouter une correction de $2"$, ce qui est égal à $0,0006$. On a:

$\sin17°44"=0,304+0,0006=0,3046$.

Pour trouver la valeur $\sin17°47"$ nous utilisons également la correction du côté droit du tableau, seulement dans ce cas nous prenons la valeur $\sin17°48"$ comme base et soustrayons la correction pour $1"$ :

$\sin17°47"=0,3057-0,0003=0,3054$.

Lors du calcul des cosinus, nous effectuons des actions similaires, mais nous regardons les degrés dans la colonne de droite et les minutes dans la colonne du bas du tableau. Par exemple, $\cos20°=0,9397$.

Il n'y a pas de corrections pour les valeurs de tangente jusqu'à $90°$ et la cotangente aux petits angles. Par exemple, trouvons $\tan 78°37"$, qui selon le tableau est égal à 4,967$.

1. Fonctions trigonométriques sont des fonctions élémentaires dont l'argument est coin. À l'aide de fonctions trigonométriques, les relations entre les côtés et coins pointus dans un triangle rectangle. Les domaines d'application des fonctions trigonométriques sont extrêmement divers. Par exemple, tout processus périodique peut être représenté comme une somme de fonctions trigonométriques (série de Fourier). Ces fonctions apparaissent souvent lors de la résolution d'équations différentielles et fonctionnelles.

2. Les fonctions trigonométriques comprennent les 6 fonctions suivantes : sinus, cosinus, tangente,cotangente, sécante Et cosécante. Pour chacune de ces fonctions il existe une fonction trigonométrique inverse.

3. Il est pratique d'introduire la définition géométrique des fonctions trigonométriques en utilisant cercle unitaire. La figure ci-dessous montre un cercle de rayon r=1. Le point M(x,y) est marqué sur le cercle. L'angle entre le rayon vecteur OM et la direction positive de l'axe Ox est égal à α.

4. Sinus l'angle α est le rapport de l'ordonnée y du point M(x,y) au rayon r :
sinα = y/r.
Puisque r=1, alors le sinus est égal à l'ordonnée du point M(x,y).

5. Cosinus l'angle α est le rapport de l'abscisse x du point M(x,y) au rayon r :
cosα=x/r

6. Tangente l'angle α est le rapport de l'ordonnée y d'un point M(x,y) à son abscisse x :
tanα=y/x,x≠0

7. Cotangente l'angle α est le rapport de l'abscisse x d'un point M(x,y) à son ordonnée y :
cotα=x/y,y≠0

8. Sécante l'angle α est le rapport du rayon r à l'abscisse x du point M(x,y) :
secα=r/x=1/x,x≠0

9. Cosécante l'angle α est le rapport du rayon r à l'ordonnée y du point M(x,y) :
cscα=r/y=1/y,y≠0

10. Dans le cercle unité, les projections x, y, les points M(x,y) et le rayon r forment un triangle rectangle, dans lequel x,y sont les jambes et r est l'hypoténuse. Par conséquent, les définitions ci-dessus des fonctions trigonométriques dans l'annexe à triangle rectangle sont formulés comme suit :
Sinus l'angle α est le rapport du côté opposé à l'hypoténuse.
Cosinus l'angle α est le rapport entre la jambe adjacente et l'hypoténuse.
Tangente L'angle α est appelé la branche opposée à celle adjacente.
Cotangente L'angle α est appelé le côté adjacent au côté opposé.
Sécante l'angle α est le rapport de l'hypoténuse à la jambe adjacente.
Cosécante l'angle α est le rapport de l'hypoténuse à la jambe opposée.

11. Graphique de la fonction sinus
y=sinx, domaine de définition : x∈R, plage de valeurs : −1≤sinx≤1

12. Graphique de la fonction cosinus
y=cosx, domaine de définition : x∈R, plage de valeurs : −1≤cosx≤1

13. Graphique de la fonction tangente
y=tanx, domaine : x∈R,x≠(2k+1)π/2, intervalle : −∞

14. Graphique de la fonction cotangente
y=cotx, domaine : x∈R,x≠kπ, intervalle : −∞

15. Graphique de la fonction sécante
y=secx, domaine : x∈R,x≠(2k+1)π/2, plage : secx∈(−∞,−1]∪∪)