Iznimka lijeve rekurzije. Raščlanjivanje Uklanjanje lijeve rekurzije na mreži

49. Ekvivalentne transformacije CS-gramatika: uklanjanje beskorisnih znakova.

Neka je dana proizvoljna CF-gramatika G . Neterminalno A ova se gramatika zove produktivan , ako postoji takav krajnji niz (uključujući prazan) koji A Þ * a neproduktivan.

Teorema. Svaka COP-gramatika je ekvivalentna COP-gramatici bez ne-terminala.

Neterminalno A gramatika G nazvao ostvariv ako postoji takav lanac a , Što S Þ * a . Inače se poziva neterminal nedostižan.

Teorema. Svaki CFG je ekvivalentan CFG-u bez nedostižnih neterminala.

Neterminalni simbol u CF-gramatici naziva se beskoristan (ili suvišan) ako je ili nedostižna ili neproduktivna.

Teorema. Svaki CFG je ekvivalentan CFG-u koji nema beskorisnih ne-terminala.

Primjer. Uklonite beskorisne simbole u gramatici

S® aC | A; A ® taksi; B ® b; C ® a.

Korak 1. Izgradnja seta ostvariv likovi: {S} ® { S, C, A}® { S, C, A, B}. Svi neterminali su dostupni. Nedostižno bez promjena gramatike.

Korak 2. Izgradnja seta produktivan likovi: {C, B}® { S, C, B}. Shvaćamo to A - nije produktivno. Izbacujemo ga i sva pravila s njim iz gramatike. Dobiti

S® aC; B ® b; C ® a.

3. korak. Izgradnja seta ostvariv simboli nove gramatike: {S} ® { S, C}. Shvaćamo to B nedostižan. Izbacujemo ga i sva pravila s njim iz gramatike. Dobiti

S® aC; C ® a.

Ovo je konačan rezultat.

50. Ekvivalentne transformacije CF-gramatika: eliminacija lijeve rekurzije, lijeva faktorizacija

Uklanjanje lijeve rekurzije

Glavna poteškoća u korištenju prediktivne analize je pronalaženje gramatike za ulazni jezik koja se može koristiti za izradu tablice analize s jedinstveno definiranim ulazima. Ponekad, uz neke jednostavne transformacije, ne-LL(1) gramatika se može reducirati na ekvivalentnu LL(1) gramatiku. Među tim transformacijama najučinkovitije su lijevo faktoriziranje i uklanjanje lijeva rekurzija. Ovdje se moraju staviti dvije napomene. Prvo, ne postaje svaka gramatika LL(1) nakon ovih transformacija, a drugo, nakon takvih transformacija, rezultirajuća gramatika može postati manje razumljiva.

Neposredna lijeva rekurzija, odnosno rekurzija oblika , može se ukloniti na sljedeći način. Prvo grupiramo A-pravila:

gdje niti jedan redak ne počinje s A. Zatim ovaj skup pravila zamijenimo s

gdje je A" novi ne-terminal. Isti lanci se mogu izvesti iz ne-terminala A kao i prije, ali sada ne postoji lijeva rekurzija. Ovaj postupak uklanja sve neposredne lijeve rekurzije, ali lijeva rekurzija koja uključuje dva ili više koraka nije uklonjena. Ispod algoritam 4.8 omogućuje uklanjanje svih lijeve rekurzije iz gramatike.

Lijeva faktorizacija

Glavna ideja iza lijeve faktorizacije je da kada nije jasno koju od dvije alternative treba upotrijebiti za odvijanje neterminala A, treba promijeniti A-pravila tako da se odluka odgodi dok ne bude dovoljno informacija za donošenje ispravne odluke. .

Ako - dva A -pravila i lanac unosa počinje s nepraznim nizom izlaza iz ne znamo hoćemo li proširiti prvim pravilom ili drugim. Odluku možete odgoditi proširenjem . Zatim, nakon analize onoga iz čega je izvedeno, možete proširiti na ili na . Lijeva faktorizirana pravila poprimaju oblik

51. Jezik Turingovog stroja.

Sastav Turingovog stroja uključuje neograničeno u oba smjera vrpca(mogući Turingovi strojevi koji imaju više beskonačnih traka) podijeljenih u ćelije, i upravljački uređaj(također se zove glava za čitanje/pisanje (GZCH)), sposoban biti u jednom od skupovi stanja. Broj mogućih stanja upravljačkog uređaja je konačan i točno zadan.

Kontrolni uređaj može se pomicati lijevo-desno duž vrpce, čitati i pisati znakove neke konačne abecede u ćelije. Posebna prazan simbol koji ispunjava sve ćelije vrpce, osim onih (konačan broj) na koje se bilježe ulazni podaci.

Upravljački uređaj radi prema pravila prijelaza, koji predstavljaju algoritam, ostvariv dati Turingov stroj. Svako prijelazno pravilo nalaže stroju, ovisno o trenutnom stanju i simbolu promatranom u trenutnoj ćeliji, da upiše novi simbol u ovu ćeliju, ode u novo stanje i pomakne jednu ćeliju ulijevo ili udesno. Neka stanja Turingovog stroja mogu se označiti kao terminal, a prijelaz na bilo koji od njih znači kraj rada, zaustavljanje algoritma.

Turingov stroj se zove deterministički ako svaka kombinacija stanja i simbola vrpce u tablici odgovara najviše jednom pravilu. Ako postoji par "simbol trake - stanje" za koji postoje 2 ili više instrukcija, takav se Turingov stroj naziva nedeterministički.

počevši i nastavljajući sa spomenutim k terminalima.

Gramatika se naziva LL(k)-gramatika ako je LL(k)-gramatika za neko k.

Primjer 4.7. Razmotrite gramatiku G = ((S, A, B), (0, 1, a, b), P, S), gdje se P sastoji od pravila

S -> A | B, A -> aAb | 0, B -> aBbb | 1.

ovdje . G nije LL(k)-gramatika ni za jedno k. Intuitivno, ako počnemo čitanjem dovoljno dugog niza znakova a , ne znamo koje je od pravila S -> A i S -> B prvo primijenjeno sve dok ne naiđemo na 0 ili 1 .

Prelazeći na preciznu definiciju LL (k)-gramatike, postavljamo i y = a k 1b 2k . Zatim zaključci

odgovaraju zaključcima (1) i (2) definicije. Prvih k znakova nizova x i y se podudaraju. Međutim, zaključak je pogrešan. Budući da je k ovdje odabran proizvoljno, G nije LL gramatika.

Posljedice definicije LL(k)-gramatike

Teorem 4.6. CS gramatika je LL(k)-gramatika ako i samo ako za dva različita pravila i od R raskrižja prazan za sve takve , Što .

Dokaz. Nužnost. Pretpostavimo da i zadovoljava uvjete iz teorema, i sadrži x . Tada, prema definiciji FIRST-a, za neke y i z postoje zaključci

(Primijetite da smo ovdje koristili činjenicu da N ne sadrži beskorisne ne-terminale, kao što se pretpostavlja za sve gramatike koje razmatramo.) Ako je |x|< k ; то y = z = e . Так как , то G не LL (k)- грамматика .

Adekvatnost. Pretpostavimo da G nije LL(k)-gramatika.

Zatim postoje dva zaključka

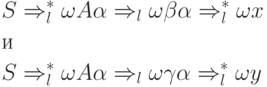
da se nizovi x i y podudaraju u prvih k pozicija, ali . Prema tome, i su različita pravila iz P i svakog od skupova I sadrži niz FIRST k (x) koji odgovara nizu FIRST k (y) .

Primjer 4.8. Gramatika G koja se sastoji od dva pravila S -> aS | a , neće biti LL(1)-gramatika, jer

PRVI 1 (aS) = PRVI 1 (a) = a.

Intuitivno se to može objasniti na sljedeći način: prilikom parsiranja niza koji počinje znakom a , vidimo samo ovaj prvi znak, ne znamo koje od pravila S -> aS ili S -> a treba primijeniti na S . S druge strane, G je LL(2)-gramatika. Doista, u zapisu upravo predstavljenog teorema, ako , tada je A = S i . Budući da su za S data samo dva navedena pravila, tada i . Kako je FIRST2(aS) = aa i FIRST2(a) = a , onda je prema zadnjem teoremu G LL (2)-gramatika.

Uklanjanje lijeve rekurzije

Glavna poteškoća u korištenju prediktivne analize je pronalaženje gramatike za ulazni jezik koja se može koristiti za izradu tablice analize s jedinstveno definiranim ulazima. Ponekad, uz neke jednostavne transformacije, ne-LL(1) gramatika se može reducirati na ekvivalentnu LL(1) gramatiku. Među tim transformacijama najučinkovitije su lijeva faktorizacija i uklanjanje lijeve rekurzije. Ovdje se moraju staviti dvije napomene. Prvo, ne postaje svaka gramatika LL(1) nakon ovih transformacija, a drugo, nakon takvih transformacija, rezultirajuća gramatika može postati manje razumljiva.

Neposredna lijeva rekurzija, odnosno rekurzija oblika , može se ukloniti na sljedeći način. Prvo grupiramo A-pravila:

gdje niti jedan redak ne počinje s A . Zatim ovaj skup pravila zamijenimo s

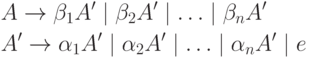
gdje je A" novi ne-terminal. Isti lanci mogu se izvesti iz ne-terminala A kao i prije, ali sada nema lijeve rekurzije. Ovaj postupak uklanja sve neposredne lijeve rekurzije, ali ne uklanja lijevu rekurziju koja uključuje dvije ili više koraka. Dano u nastavku algoritam 4.8 omogućuje vam uklanjanje svih lijevih rekurzija iz gramatike.

Algoritam 4.8. Uklanjanje lijeve rekurzije.

Ulaz. COP-gramatika G bez e-pravila (forme A -> e ).

Izlaz. COP-gramatika G" bez lijeve rekurzije, ekvivalentna G .

metoda. Slijedite korake 1 i 2.

(1) Rasporedite ne-terminale gramatike G proizvoljnim redoslijedom.

(2) Provedite sljedeći postupak:

Nakon (i-1)-te iteracije vanjske petlje u koraku 2 za bilo koje pravilo oblika , gdje je k< i , выполняется s >k . Kao rezultat toga, u sljedećoj iteraciji (za i), unutarnja petlja (za j) sekvencijalno povećava donju granicu za m u bilo kojem pravilu sve dok m >= i . Zatim, nakon uklanjanja neposredne lijeve rekurzije za A i -pravila, m postaje veće od i.

Gramatika koja sadrži lijevu rekurziju nije LL(1) gramatika. Razmotrite pravila

A→ aa(lijeva rekurzija u A)

A→ a

Ovdje a znak prethodnika za obje neterminalne varijante A. Slično tome, gramatika koja sadrži lijevu rekurzivnu petlju ne može biti LL(1) gramatika, na primjer

A→ PRIJE KRISTA

B→ CD

C→ AE

Gramatika koja sadrži lijevu rekurzivnu petlju može se pretvoriti u gramatiku koja sadrži samo izravnu lijevu rekurziju, a nadalje, uvođenjem dodatnih ne-terminala, lijeva rekurzija može se potpuno eliminirati (zapravo, zamijenjena je desnom rekurzijom, koja nije problem s obzirom na LL(1) -svojstva).

Kao primjer, razmotrite gramatiku s generativnim pravilima

S→ aa

A→ bb

B→ CC

C→ Dd

C→ e

D→ Az

koji ima lijevu rekurzivnu petlju koja uključuje A, B, C, D. Da bismo ovu petlju zamijenili izravnom lijevom rekurzijom, poredamo neterminale na sljedeći način: S, A, B, C, D.

Razmotrite sva pravila generiranja obrasca

Xi→ Xj γ,

Gdje Xi I Xj su ne-terminali, i γ – niz terminalnih i neterminalnih znakova. S obzirom na pravila za koja j ≥ i, nije poduzeta nikakva radnja. Međutim, ova nejednakost ne može vrijediti za sva pravila ako postoji lijeva rekurzivna petlja. Redoslijedom koji smo odabrali, imamo posla s jednim pravilom:

D→ Az

jer A prethodio D ovim redom. Sada počnimo sa zamjenom A, koristeći sva pravila koja imaju A s lijeve strane. Kao rezultat toga, dobivamo

D→ bbz

Jer B prethodio D kod naručivanja, proces se ponavlja, dajući pravilo:

D→ ccbz

Zatim se ponavlja još jednom i daje dva pravila:

D→ ecbz

D→ Ddcbz

Sada konvertirana gramatika izgleda ovako:

S→ aa

A→ bb

B→ CC

C→ Dd

C→ e

D→ Ddcbz

D→ ecbz

Sva ova pravila generiranja imaju traženi oblik, a lijeva rekurzivna petlja zamijenjena je izravnom lijevom rekurzijom. Kako bismo uklonili izravnu lijevu rekurziju, uvodimo novi neterminalni simbol Z i promijeniti pravila

D→ ecbz

D→ Ddcbz

D→ ecbz

D→ ecbzZ

Z→ dcbz

Z→ dcbzZ

Imajte na umu da prije i poslije transformacije D generira regularni izraz

(ecbz) (dcbz)*

Generalizirajući, može se pokazati da ako je neterminal A pojavljuje se na lijevoj strani r+ s generiranje pravila, r od kojih koriste izravnu lijevu rekurziju, i s- ne, tj.

A→ Aα 1, A→ Aα 2,..., A→ Aα r

A→ β 1, A→ β 2,..., A→ β s

tada se ova pravila mogu zamijeniti sljedećim:

Neslužbeni dokaz je da prije i poslije transformacije A generira regularni izraz ( β 1 | β 2 |... | β s) ( α 1 | α 2 |... | α r)*

Treba primijetiti da eliminacijom lijeve rekurzije (ili lijeve rekurzivne petlje), još uvijek ne dobivamo LL(1) gramatiku, jer za neke ne-terminale, na lijevoj strani pravila rezultirajućih gramatika, postoje alternativni desni dijelovi koji počinju istim znakovima. Stoga, nakon eliminacije lijeve rekurzije, treba nastaviti transformaciju gramatike u LL(1) oblik.

17. Pretvaranje gramatika u LL(1) oblik. Faktorizacija.

Faktorizacija

U mnogim situacijama, gramatike koje nemaju značajku LL(1) mogu se pretvoriti u LL(1) gramatike korištenjem procesa faktorizacije. Razmotrimo primjer takve situacije.

P→ početak D; S kraj

D→ d, D

D→ d

S→ s; S

S→ s

U procesu faktorizacije više pravila za jedan neterminal na lijevoj strani, čija desna strana počinje istim simbolom (nizom simbola) zamjenjujemo jednim pravilom, gdje na desnoj strani zajednički početak slijedi dodatno uvedeni neterminal. Gramatika je također dopunjena pravilima za dodatni neterminal, prema kojima se iz njega izvode različiti “ostaci” izvorne desne strane pravila. Za gornju gramatiku, ovo bi dalo sljedeću LL(1) gramatiku:

P→ početak D; S kraj

D→ d X x)

x→ , D(prema 1. pravilu za D izvorna gramatika za d slijedi, D)

x→ ε (prema 2. pravilu za D izvorna gramatika za d ništa (prazan niz)

S→ s Y(uvodimo dodatni ne-terminal Y)

Y→ ; S(prema 1. pravilu za C izvorna gramatika za s slijedi; C)

Y→ ε (prema 2. pravilu za C izvorna gramatika za s ništa (prazan niz)

Slično, generiranje pravila

S→ aSb

S→ asc

S→ ε

mogu se faktoriziranjem pretvoriti u pravila

S→ aSX

S→ ε

x→ b

x→ c

a rezultirajuća gramatika će biti LL(1). Međutim, proces faktorizacije ne može se automatizirati proširivanjem na opći slučaj. Sljedeći primjer pokazuje što se može dogoditi. Razmotrite pravila

1. P→ Qx

2. P→ Ry

3. Q→ kvadratnih metara

4. Q→ q

5. R→ sRn

6. R→ r

Oba skupa znakova vodiča za dvije opcije P sadržavati s, i pokušavajući "izdržati s izvan zagrada", zamjenjujemo Q I R u desnim dijelovima pravila 1 i 2:

P→ sQmx

P→ sRny

P→ qx

P→ ry

Ova pravila mogu se zamijeniti sljedećim:

P→ qx

P→ ry

P→ sp 1

P 1 → Qmx

P 1 → Rny

Pravila za P1 slično izvornim pravilima za P i imaju preklapajuće skupove simbola vodiča. Ova pravila možemo transformirati na isti način kao i pravila za P:

P 1 → sQmmx

P 1 → qmx

P 1 → sRny

P 1 → rny

Faktoring, dobivamo

S rekurzivnim postupkom parsiranja odozgo prema dolje može se pojaviti problem beskonačne petlje.

U gramatici za aritmetičke operacije, primjena drugog pravila uzrokovat će petlju postupka parsiranja. Takve se gramatike nazivaju lijevo-rekurzivne. Kaže se da je gramatika lijevo-rekurzivna ako sadrži ne-terminal A za koji postoji derivacija A=>+Aa. U jednostavnim slučajevima, lijeva rekurzija se poziva prema pravilima forme

U tom se slučaju uvodi novi neterminal, a izvorna pravila zamjenjuju se sljedećim.

(ako postoji neterminal A za koji postoji izlaz A→+Aa u 1 ili više koraka). Lijeva rekurzija može se izbjeći transformacijom gramatike.

Na primjer, produkcije A→Aa

Može se zamijeniti s ekvivalentom:

Za takav slučaj postoji algoritam koji isključuje lijevu rekurziju:

1) definirajte neki poredak na skupu neterminala (A 1 , A 2 , …, A n)

2) uzimamo svaki ne-terminal ako za njega postoji proizvodnja koja uzima u obzir ne-terminal s lijeve strane, i transformiramo gramatiku:

za i:=1 do n učiniti

za j:=1 do i-1 učiniti

ako je Ai → Ajγ onda Ai→δ1γ

│ δkγ, gdje

Aj → δ1│ δ2│ …│ δk

3) isključite sve slučajeve neposredne lijeve rekurzije (pravilo 1)

Da. algoritam pomaže u izbjegavanju petlji.

Eliminacija lijeve rekurzije iz gramatike aritmetičkih izraza i opći oblik pravila za isključivanje lijeve rekurzije:

Opći prikaz pravila isključenja lijeve rekurzije

Lijeva faktorizacija.

Potrebne su LL(1) gramatike kako bi se odabrala prava proizvodnja za raščlanjivanje od vrha prema dolje, tako da ne dolazi do petlji.

Ponekad je moguće pretvoriti gramatiku u LL(1) oblik pomoću metode lijevog faktoriziranja.

Na primjer: S → ako B onda S

│if B then S else S

Ove produkcije krše uvjet LL(1)-gramatika. Ova se gramatika može pretvoriti u oblik LL(1).

S → ako je B onda S Rep

Općenito, ova se transformacija može definirati na sljedeći način:

uvodimo novi neterminal B, za koji

| β N Lijeva faktorizacija se može primijeniti na B. Ovaj postupak se ponavlja sve dok je izbor proizvoda nesiguran (tj. dok se u njemu ne može nešto promijeniti).

Izgradnja PRVOG skupa

Prvi skup za ne-terminal definira skup terminala s kojima ovaj ne-terminal može započeti.

1. Ako je x terminal, tada je first(x)=(x). Budući da prvi znak niza iz jednog terminala može biti samo sam terminal.

2. Ako gramatika sadrži pravilo Hà e, tada skup first(h) uključuje e. To znači da X može početi s praznim nizom, odnosno ne može uopće postojati.

3. Za sve produkcije oblika XàY1 Y2 … Yk radimo sljedeće. Skupu first(X) dodajemo skup first(Yi) dok first(Yi-1) ne sadrži e i first(Yi) ne sadrži e. U ovom slučaju, i se mijenja od 0 do k. Ovo je neophodno, jer ako Yi-1 može biti odsutan, onda je potrebno saznati gdje će cijeli niz započeti u ovom slučaju.

LL(k)-svojstvo nameće velika ograničenja gramatici. Ponekad je moguće transformirati gramatiku tako da rezultirajuća gramatika ima svojstvo LL(1) . Takva transformacija nipošto nije uvijek uspješna, ali ako ste uspjeli dobiti LL(1) gramatiku, tada možete koristiti metodu rekurzivnog spuštanja bez vraćanja unatrag za izgradnju analizatora.

Pretpostavimo da trebamo izgraditi analizator za jezik generiran sljedećom gramatikom:

E → E + T | E – T | T

T→T*F | T/F | F

F → br | (E)

Postavite terminale PRVI(T) također pripadaju skupu PRVI (E+T), pa nije moguće jednoznačno odrediti redoslijed poziva procedura koje se moraju izvršiti prilikom parsiranja ulaznog niza. Problem je u tome što ne-terminal E pojavljuje se na prvoj poziciji desne strane pravila čija je lijeva strana također E. U takvoj situaciji, ne-terminal E naziva se izravno lijevo-rekurzivno.

Neterminalno A COP-gramatike G nazvao lijevo rekurzivno ako gramatika ima derivaciju A =>* Ajme.

Gramatika koja ima barem jedno lijevo-rekurzivno pravilo ne može biti LL(1)-gramatika.

S druge strane, poznato je da je svaki CS-jezik definiran barem jednom nelijevo-rekurzivnom gramatikom.

1. Lijevo rekurzivni eliminacijski algoritam

Neka G = (N, T, P, S)– CS-gramatika i pravilo A→Ajme 1 | Ajme 2 | … | Ajme n | v 1 | v 2 | … | v m predstavlja sva pravila iz P koji sadrži A na lijevoj strani, a niti jedan lančić v ja ne počinje s ne-terminalom A.

Dodajmo u set N još jedan ne-terminal A" i zamijeniti pravila koja sadrže A na lijevoj strani, na sljedeće:

A→v 1 | v 2 | … | v m | v 1 A' | v 2 A' | … | v m A"

A' → w 1 | w 2 | … | w n | w 1 A' | w 2 A' | …| w n A"

Može se dokazati da je dobivena gramatika ekvivalentna izvornoj.

Kao rezultat primjene ove transformacije na gornju gramatiku koja opisuje aritmetičke izraze, dobivamo sljedeću gramatiku:

E → T | TE"

E" → + T | + TE"

T → F | FT"

T"→ * F | * FT"

F → (E) | br

Lako je pokazati da rezultirajuća gramatika ima svojstvo LL(1).

Drugi sličan problem povezan je s činjenicom da dva pravila za isti ne-terminal počinju istim znakovima.

Na primjer,

S → if E then S else S

S → ako E zatim S

U ovom slučaju, dodajmo još jedan ne-terminal koji će odgovarati različitim završecima ovih pravila. Dobijamo sljedeća pravila:

S → ako E zatim S S’

S" →

S"→ drugo S

Za rezultirajuću gramatiku može se implementirati metoda rekurzivnog spuštanja.

1. 9.1.4. Rekurzivno spuštanje s vraćanjem unatrag.

0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 PRVI ne sijeku, što je složen proces, pa u praksi trik tzv rekurzivno spuštanje s vraćanjem unatrag .

Da bi se to postiglo, leksički analizator je predstavljen kao objekt koji, uz tradicionalne metode, ima skenirati, Sljedeći itd. postoji i konstruktor kopiranja. Zatim, u svim situacijama u kojima može doći do dvosmislenosti, prije početka parsiranja treba zapamtiti trenutno stanje leksičkog analizatora (tj. napraviti kopiju leksičkog analizatora) i nastaviti s parsiranjem teksta, s obzirom na to da imamo posla s prvim mogućim konstrukcija u ovoj situaciji. Ako ova analiza ne uspije, vratite stanje leksera i pokušajte ponovo analizirati isti fragment sa sljedećom gramatikom itd. Ako sve analize ne uspiju, javlja se pogreška.

Ova metoda raščlanjivanja potencijalno je sporija od rekurzivnog spuštanja bez povratnog praćenja, ali u ovom slučaju moguće je zadržati gramatiku u izvornom obliku i uštedjeti trud programera.