Определение диагонали параллелограмма. Определение параллелограма и его свойства

Понятие параллелограмма

Определение 1

Параллелограмм — это четырехугольник, в котором противоположные стороны параллельны между собой (рис. 1).

Рисунок 1.

Параллелограмм имеет два основных свойства. Рассмотрим их без доказательства.

Свойство 1: Противоположные стороны и углы параллелограмма равны, соответственно, между собой.

Свойство 2: Диагонали, проведенные в параллелограмме, делятся пополам их точкой пересечения.

Признаки параллелограмма

Рассмотрим три признака параллелограмма и представим их в виде теорем.

Теорема 1

Если две стороны четырехугольника равны между собой, а также параллельны, то этот четырехугольник будет параллелограммом.

Доказательство.

Пусть нам дан четырехугольник $ABCD$. В котором $AB||CD$ и $AB=CD$ Проведем в нем диагональ $AC$ (рис. 2).

Рисунок 2.

Рассмотрим параллельные прямые $AB$ и $CD$ и их секущую $AC$. Тогда

[angle CAB=angle DCA]

как накрест лежащие углы.

По $I$ признаку равенства треугольников,

так как $AC$ — их общая сторона, а $AB=CD$ по условию. Значит

[angle DAC=angle ACB]

Рассмотрим прямые $AD$ и $CB$ и их секущую $AC$, по последнему равенству накрест лежащих углов получим, что $AD||CB$.}Следовательно, по определению $1$, данный четырехугольник является параллелограммом.

Теорема доказана.

Теорема 2

Если противоположные стороны четырехугольника равны между собой, то он является параллелограммом.

Доказательство.

Пусть нам дан четырехугольник $ABCD$. В котором $AD=BC$ и $AB=CD$. Проведем в нем диагональ $AC$ (рис. 3).

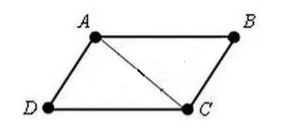
Рисунок 3.

Так как $AD=BC$, $AB=CD$, а $AC$ — общая сторона, то по $III$ признаку равенства треугольников,

[triangle DAC=triangle ACB]

[angle DAC=angle ACB]

Рассмотрим прямые $AD$ и $CB$ и их секущую $AC$, по последнему равенству накрест лежащих углов получим, что $AD||CB$.Следовательно, по определению $1$, данный четырехугольник является параллелограммом.

[angle DCA=angle CAB]

Рассмотрим прямые $AB$ и $CD$ и их секущую $AC$, по последнему равенству накрест лежащих углов получим, что $AB||CD$.Следовательно, по определению 1, данный четырехугольник является параллелограммом.

Теорема доказана.

Теорема 3

Если диагонали, проведенные в четырехугольнике, своей точкой пересечения делятся на две равные части, то этот четырехугольник является параллелограммом.

Доказательство.

Пусть нам дан четырехугольник $ABCD$. Проведем в нем диагонали $AC$ и $BD$. Пусть они пересекаются в точке $O$ (рис. 4).

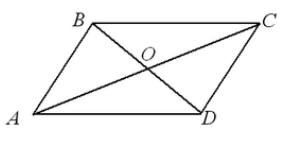
Рисунок 4.

Так как, по условию $BO=OD, AO=OC$, а углы $angle COB=angle DOA$ как вертикальные, то, по $I$ признаку равенства треугольников,

[triangle BOC=triangle AOD]

[angle DBC=angle BDA]

Рассмотрим прямые $BC$ и $AD$ и их секущую $BD$, по последнему равенству накрест лежащих углов получим, что $BC||AD$. Также $BC=AD$. Следовательно, по теореме $1$, данный четырехугольник является параллелограммом.

Муниципальное бюджетное общеобразовательное учреждение

Савинская средняя общеобразовательная школа

Исследовательская работа

Параллелограмм и его новые свойства

Выполнила: ученица 8Б класса

МБОУ Савинская СОШ

Кузнецова Светлана,14 лет

Руководитель: учитель математики

Тульчевская Н.А.

п. Савино

Ивановская область, Россия

2016г.

I. Введение __________________________________________________стр 3

II. Из истории параллелограмма ___________________________________стр 4

III Дополнительные свойства параллелограмма ______________________стр 4

IV. Доказательство свойств _____________________________________ стр 5

V. Решение задач с использованием дополнительных свойств __________стр 8

VI. Применение свойств параллелограмма в жизни ___________________стр 11

VII. Заключение _________________________________________________стр 12

VIII. Литература _________________________________________________стр 13

Введение

«Среди равных умов

при одинаковости прочих условий

превосходит тот, кто знает геометрию»

(Блез Паскаль).

Во время изучения темы «Параллелограмм» на уроках геометрии мы рассмотрели два свойства параллелограмма и три признака, но когда мы начали решать задачи, то оказалось, что этого недостаточно.

У меня возник вопрос, а есть ли у параллелограмма еще свойства, и как они помогут при решении задач.

И я решила изучить дополнительные свойства параллелограмма и показать, как их можно применить для решения задач.

Предмет исследования: параллелограмм

Объект исследования: свойства параллелограммаЦель работы:

формулировка и доказательство дополнительных свойств параллелограмма, которые не изучаются в школе;

применение этих свойств для решения задач.

Задачи:

Изучить историю возникновения параллелограмма и историю развития его свойств;

Найти дополнительную литературу по исследуемому вопросу;

Изучить дополнительные свойства параллелограмма и доказать их;

Показать применение этих свойств для решения задач;

Рассмотреть применение свойств параллелограмма в жизни.Методы исследования:

Работа с учебной и научно – популярной литературой, ресурсами сети Интернет;

Изучение теоретического материала;

Выделение круга задач, которые можно решать с использованием дополнительных свойств параллелограмма;

Наблюдение, сравнение, анализ, аналогия.

Продолжительность исследования: 3 месяца: январь-март 2016г

1. Из истории параллелограмма

В учебнике геометрии мы читаем следующее определение параллелограмма: параллелограмм – это такой четырехугольник, у которого противоположные стороны попарно параллельны

Слово «параллелограмм» переводится как «параллельные линии» (от греческих слов Parallelos — параллельный и gramme — линия), этот термин был введен Евклидом. В своей книге «Начала» Евклид доказал следующие свойства параллелограмма: противоположные стороны и углы параллелограмма равны, а диагональ делит его пополам. О точке пересечения параллелограмма Евклид не упоминает. Только к концу средних веков была разработана полная теория параллелограммов И лишь в XVII веке в учебниках появились теоремы о параллелограммах, которые доказываются с помощью теоремы Евклида о свойствах параллелограмма.

III Дополнительные свойства параллелограмма

В учебнике по геометрии даны только 2 свойства параллелограмма:

Противоположные углы и стороны равны

Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам

В различных источниках по геометрии можно встретить следующие дополнительные свойства:

Сумма соседних углов параллелограмма равна 180 0

Биссектриса угла параллелограмма отсекает от него равнобедренный треугольник;

Биссектрисы противоположных углов параллелограмма лежат на параллельных прямых;

Биссектрисы соседних углов параллелограмма пересекаются под прямым углом;

Биссектрисы всех углов параллелограмма при пересечении образуют прямоугольник;

Расстояния от противоположных углов параллелограмма до одной и той же его диагонали равны.

Если в параллелограмме соединить противоположные вершины с серединами противоположных сторон, то получится еще один параллелограмм.

Сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его смежных сторон.

Если в параллелограмме из двух противоположных углов провести высоты, то получится прямоугольник.

IVДоказательство свойств параллелограмма

Сумма соседних углов параллелограмма равна 180 0

Дано:

ABCD – параллелограмм

Доказать:

A +B =

Доказательство:

А и B –внутренние односторонние углы при параллельных прямых ВС АD и секущей АВ, значит, A +B =

2

Дано: АBCD —параллелограмм,

АК -биссектриса А.

Доказать: АВК – равнобедренный

Доказательство:

1) 1=3 (накрест лежащие при ВСAD и секущей AK),

2) 2=3 т. к. АК – биссектриса,

значит 1=2.

3) АВК – равнобедренный т. к. 2 угла треугольника равны

. Биссектриса угла параллелограмма отсекает от него равнобедренный треугольник

3

Дано: АВСD – параллелограмм,

АК – биссектриса A,

СР — биссектриса C.

Доказать: АК ║ СР

Доказательство:

1) 1=2 т. к. АК-биссектриса

2) 4=5 т.к. СР – биссектриса

3) 3=1 (накрест лежащие углы при

ВС ║ АD и АК-секущей),

4) A=C (по свойству параллелограмма), значит2=3=4=5.

4) Из п. 3 и 4 следует, что 1=4, а эти углы соответственные при прямых АК и СР и секущей ВС,

значит, АК ║ СР (по признаку параллельности прямых)

. Биссектрисы противоположных углов параллелограмма лежат на параллельных прямых

Биссектрисы соседних углов параллелограмма пересекаются под прямым углом

Дано: АВСD — параллелограмм,

АК-биссектриса A,

DР-биссектриса D

Доказать: DР АК.

Доказательство:

1) 1=2, т.к. АК — биссектриса

Пусть, 1=2=x, тогда А=2x,

2) 3=4, т.к. DР – биссектриса

Пусть, 3=4= у, тогда D=2y

3) A+D=180 0 , т.к. сумма соседних углов параллелограмма равна 180

2) Рассмотрим AОD

1+3=90 0 , тогда

5. Биссектрисы всех углов параллелограмма при пересечении образуют прямоугольник

Дано: АВСD — параллелограмм, АК-биссектриса A,

DР-биссектриса D,

CM -биссектриса C,

BF -биссектриса B.

Доказать: KRNS-прямоугольник

Доказательство:

Исходя из предыдущего свойства 8=7=6=5=90 0 ,

значит KRNS-прямоугольник.

Расстояния от противоположных углов параллелограмма до одной и той же его диагонали равны.

Дано: ABCD-параллелограмм, АС-диагональ.

ВК АС, DPAC

Доказать: BК=DР

Доказательство: 1)DCР=КAB, как внутренние накрест лежащие при АВ ║ СD и секущей АС.

2) AКB=CDР (по стороне и двум прилежащим к ней углам АВ=СD CDР=ABК).

А в равных треугольниках соответственные стороны равны, значит DР=BК.

Если в параллелограмме соединить противоположные вершины с серединами противоположных сторон, то получится еще один параллелограмм.

Дано: ABCD-параллелограмм.

Доказать: ВКDР – параллелограмм.

Доказательство:

1) BР=КD (AD=BC, точки К и Р

делят эти стороны пополам)

2) ВР ║ КD (лежат на АD BC)

Если в четырехугольнике противоположные стороны равны и параллельны, значит, этот четырехугольник -параллелограмм.

Если в параллелограмме из двух противоположных углов провести высоты, то получится прямоугольник.

Сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его смежных сторон.

Дано: ABCD – параллелограмм. BD и AC — диагонали.

Доказать: АС 2 +ВD 2 =2(AB 2 + AD 2 )

Доказательство: 1)АСК:AC²= +

2)BРD:BD 2 =BР 2 + РD 2 (по теореме Пифагора)

3)AC²+BD²=СК²+AК²+BР²+РD²

4) СК = ВР = Н(высота)

5) АС 2 +ВD 2 =H 2 +AК 2 +H 2 +РD 2

6)ПустьDК=AР=х, тогда CКD:H 2 =CD 2 – х 2 по теореме Пифагора)

7) АС²+ВD² = СD 2 — х²+ АК 1 ²+CD 2 -х 2 +РD 2 ,

АС²+ВD²=2СD 2 -2х 2 +AК 2 +РD 2

8) AК=AD+х,РD=AD-х,

АС²+ВD² =2CD 2 -2х 2 +(AD+х) 2 +(AD-х) 2 ,

АС²+ВD²=2СD²-2х² +AD 2 +2ADх+х 2 +AD 2 -2ADх+х 2 ,АС²+ВD²=2CD 2 +2AD 2 =2(CD 2 +AD 2 ).

V. Решение задач с использованием этих свойств

Точка пересечения биссектрис двух углов параллелограмма, прилежащих к одной стороне, принадлежит противоположной стороне. Меньшая сторона параллелограмма равна 5 . Найдите его большую сторону.

Дано: ABCD – параллелограмм,

АК – биссектриса А,

DК – биссектриса D, АВ=5

Найти: ВС

ешение

Решение

Т.к. АК — биссектриса А, то АВК – равнобедренный.

Т.к. DК – биссектриса D, то DCK- равнобедренный

DC=CК= 5

Тогда, ВС=ВК+СК=5+5 = 10

Ответ: 10

2. Найдите периметр параллелограмма, если биссектриса одного из его углов делит сторону параллелограмма на отрезки 7 см и 14 см.

1 случай

Дано: А,

ВК=14 см, КС=7 см

Найти: Р параллелограмма

Решение

ВС=ВК+КС=14+7=21 (см)

Т.к. АК – биссектриса А, то АВК – равнобедренный.

АВ=ВК= 14 см

Тогда Р=2 (14+21) =70 (см)

случай

Дано:ABCD – параллелограмм,

DК – биссектриса D,

ВК=14 см, КС=7 см

Найти: Р параллелограмма

Решение

ВС=ВК+КС=14+7=21 (см)

Т.к. DК – биссектриса D, то DCK- равнобедренный

DC=CК= 7

Тогда, Р= 2 (21+7) = 56 (см)

Ответ: 70см или 56 см

3.Стороны параллелограмма равны 10 см и 3 см. Биссектрисы двух углов, прилежащих к большей стороне, делят противоположную сторону на три отрезка. Найдите эти отрезки.

1 случай: биссектрисы пересекаются вне параллелограмма

Дано:ABCD – параллелограмм, АК – биссектриса А,

DК – биссектриса D, АВ=3 см, ВС=10 см

Найти: ВМ, МN, NC

Решение

Т.к. АМ — биссектриса А, то АВМ – равнобедренный.

Т.к. DN – биссектриса D, то DCN- равнобедренный

DC=CN= 3

Тогда, МN= 10 – (BM+NC) = 10 – (3+3)=4 см

2 случай:биссектрисы пересекаются внутри параллелограмма

Т.к. АN — биссектриса А, то АВN – равнобедренный.

АВ=ВN= 3 D

А раздвижную решетку – отодвигать на необходимое расстояние в дверном проеме

Параллелограммный механизм — четырёхзвенный механизм, звенья которого составляют параллелограмм. Применяется для реализации поступательного движения шарнирными механизмами.

Параллелограмм с неподвижным звеном — одно звено неподвижно, противоположное совершает качательное движение, оставаясь параллельным неподвижному. Два параллелограмма, соединённых друг за другом, дают конечному звену две степени свободы, оставляя его параллельным неподвижному.

Примеры: стеклоочистители автобусов, погрузчики, штативы, подвесы, автомобильные подвески.

Параллелограмм с неподвижным шарниром — используется свойство параллелограмма сохранять постоянное соотношение расстояний между тремя точками. Пример: чертёжный пантограф — прибор для масштабирования чертежей.

Ромб — все звенья одинаковой длины, приближение (стягивание) пары противоположных шарниров приводит к раздвиганию двух других шарниров. Все звенья работают на сжатие.

Примеры — автомобильный ромбовидный домкрат, трамвайный пантограф.

Ножничный или X-образный механизм, также известный как Нюрнбергские ножницы — вариант ромба — два звена, соединённые посередине шарниром. Достоинства механизма — компактность и простота, недостаток — наличие двух пар скольжения. Два (и более) таких механизма, соединённые последовательно, образуют в середине ромб(ы). Применяется в подъёмниках, детских игрушках.

VII Заключение

Кто с детских лет занимается математикой,

тот развивает внимание, тренирует свой мозг,

свою волю, воспитывает в себе настойчивость

и упорство в достижении цели

А. Маркушевич

В ходе работы я доказала дополнительные свойства параллелограмма.

Я убедилась, что применяя эти свойства, можно решать задачи быстрее.

Я показала, как применяются эти свойства на примерах решения конкретных задач.

Я узнала много нового о параллелограмме, чего нет в нашем учебнике геометрии

Я убедилась в том, что знания геометрии очень важны в жизни на примерах применения свойств параллелограмма.

Цель моей исследовательской работы выполнена.

О том, насколько важны математические знания, говорит тот факт, что была учреждена премия тому, кто издаст книгу о человеке, который всю жизнь прожил без помощи математики. Эту премию до сих пор не получил ни один человек.

VIII Литература

1. ПогореловА.В. Геометрия 7-9: учебник для общеобразоват. учреждений-М.: Просвещение, 2014г

   Л.С.Атанасян и др. Геометрия. Доп. Главы к учебнику 8 кл.: учеб. пособие для учащихся школ и классов с углубл. изуч.математики. – М.: Вита-пресс, 2003

   Ресурсы сети Интернет

   материалы Википедии

Тема урока

• Свойство диагоналей параллелограмма.

Цели урока

• Познакомиться с новыми определениями и вспомнить некоторые уже изученные.
• Сформулировать и доказать свойство диагоналей параллелограмма.
• Научиться применять свойства фигур при решении задач.
• Развивающие – развить внимание учащихся, усидчивость, настойчивость, логическое мышление, математическую речь.
• Воспитательные — посредством урока воспитывать внимательное отношение друг к другу, прививать умение слушать товарищей, взаимовыручке, самостоятельность.

Задачи урока

• Проверить умение учащихся решать задачи.

План урока

1. Вступительное слово.
2. Повторение ранее изученного материала.
3. Параллелограмм, его свойства и признаки.
4. Примеры задач.
5. Самостоятельная проверка.

Введение

«Крупное научное открытие дает решение крупной проблемы, но и в решении любой задачи присутствует крупица открытия».

Свойство противолежащих сторон параллелограмма

У параллелограмма противолежащие стороны равны.

Доказательство.

Пусть ABCD – данный параллелограмм. И пусть его диагонали пересекаются в точке O.Так как Δ AOB = Δ COD по первому признаку равенства треугольников (∠ AOB = ∠ COD, как вертикальные, AO=OC, DO=OB, по свойству диагоналей параллелограмма), то AB=CD. Точно также из равенства треугольников ВОС и DOA, следует что BC=DA. Теорема доказана.

Свойство противолежащих углов параллелограмма

У параллелограмма противолежащие углы равны.

Доказательство.Пусть ABCD – данный параллелограмм . И пусть его диагонали пересекаются в точке O.Из доказанного в теореме о свойства противолежащих сторон параллелограмма Δ ABC = Δ CDA по трем сторонам (AB=CD, BC=DA из доказанного, AC – общая). Из равенства треугольников следует, что ∠ ABC = ∠ CDA.Так же доказывается, что ∠ DAB = ∠ BCD, которое следует из ∠ ABD = ∠ CDB. Теорема доказана.

Свойство диагоналей параллелограмма

Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам.

Доказательство.

Пусть ABCD – данный параллелограмм. Проведем диагональ AC. Отметим на ней середину O. На продолжении отрезка DO отложим отрезок OB 1 , равный DO.По предыдущей теореме AB 1 CD – параллелограмм. Поэтому, прямая AB 1 параллельна DC. Но через точку A можно провести только одну прямую, параллельную DC. Значит, прямая AB 1 совпадает с прямой AB.Также доказывается, что BC 1 совпадает с BC. Значит, точка С совпадает с С 1 . параллелограмм ABCD совпадает с параллелограммом AB 1 CD. Следовательно, диагонали параллелограмма пересекаются и точкой пересечения делятся пополам. Теорема доказана.

В учебниках для обычных школ (например, в Погорелове) доказывается она так: диагонали делят параллелограмм на 4 треугольника. Рассмотрим одну пару и выясним — они равны: основания у них — противоположные стороны, прилежащие к нему соответствующие углы равны как вертикальные при параллельных прямых. То есть отрезки диагоналей попарно равны. Всё.

Всё ли?Выше доказано, что точка пересечения делит диагонали пополам — если существует. Само её существование приведённое рассуждение не доказывает ни в коей мере. То есть часть теоремы «диагонали параллелограмма пересекаются» остаётся недоказанной.

Забавно, что доказать эту часть намного сложнее. Следует это, кстати, из более общего результата: у любого выпуклого четырёхугольника диагонали будут пересекаться, у любого невыпуклого — не будут.

О равенстве треугольников по стороне и двум прилежащим к ней углам (второй признак равенства треугольников) и другие.

Теореме о равенстве двух треугольников по стороне и двум прилежащим к ней углам Фалес нашел важное практическое применение. В гавани Милета был построен дальномер, определяющий расстояние до корабля в море. Он представлял собой три вбитых колышка А, В и С (АВ = ВС) и размеченную прямую СК, перпендикулярную.СА. При появлении корабля на прямой СК находили точку D такую, чтобы точки D, .В и Е оказывались на одной прямой. Как ясно из чертежа, расстояние CD на земле является искомым расстоянием до корабля.

Вопросы

1. Диагонали квадрата точкой пересечения делятся пополам?
2. Диагонали параллелограмма равны?
3. Противолежащие углы параллелограмма равны?
4. Сформулируйте определение параллелограмма?
5. Сколько признаков параллелограмма?
6. Может ли ромб быть параллелограмом?

Список использованных источников

1. Кузнецов А. В., учитель математики (5-9 класс), г. Киев
2. «Единый государственный экзамен 2006. Математика. Учебно-тренировочные материалы для подготовки учащихся/ Рособрнадзор, ИСОП – М.: Интеллект-Центр, 2006»
3. Мазур К. И. «Решение основных конкурсных задач по математике сборника под редакцией М. И. Сканави»
4. Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев, Э. Г. Позняк, И. И. Юдина «Геометрия, 7 – 9: учебник для общеобразовательных учреждений»

Над уроком работали

Кузнецов А. В.

Потурнак С.А.

Евгений Петров

Поставить вопрос о современном образовании, выразить идею или решить назревшую проблему Вы можете на Образовательном форуме , где на международном уровне собирается образовательный совет свежей мысли и действия. Создав блог, Вы не только повысите свой статус, как компетентного преподавателя, а и сделаете весомый вклад в развитие школы будущего. Гильдия Лидеров Образования открывает двери для специалистов высшего ранга и приглашает к сотрудничеству в направлении создания лучших в мире школ.

Предмети > Математика > Математика 8 класс

Видеокурс «Получи пятерку» включает все темы, необходимые для успешной сдачи ЕГЭ по математике на 60-65 баллов. Полностью все задачи 1-13 Профильного ЕГЭ по математике. Подходит также для сдачи Базового ЕГЭ по математике. Если вы хотите сдать ЕГЭ на 90-100 баллов, вам надо решать часть 1 за 30 минут и без ошибок!

Курс подготовки к ЕГЭ для 10-11 класса, а также для преподавателей. Все необходимое, чтобы решить часть 1 ЕГЭ по математике (первые 12 задач) и задачу 13 (тригонометрия). А это более 70 баллов на ЕГЭ, и без них не обойтись ни стобалльнику, ни гуманитарию.

Вся необходимая теория. Быстрые способы решения, ловушки и секреты ЕГЭ. Разобраны все актуальные задания части 1 из Банка заданий ФИПИ. Курс полностью соответствует требованиям ЕГЭ-2018.

Курс содержит 5 больших тем, по 2,5 часа каждая. Каждая тема дается с нуля, просто и понятно.

Сотни заданий ЕГЭ. Текстовые задачи и теория вероятностей. Простые и легко запоминаемые алгоритмы решения задач. Геометрия. Теория, справочный материал, разбор всех типов заданий ЕГЭ. Стереометрия. Хитрые приемы решения, полезные шпаргалки, развитие пространственного воображения. Тригонометрия с нуля — до задачи 13. Понимание вместо зубрежки. Наглядное объяснение сложных понятий. Алгебра. Корни, степени и логарифмы, функция и производная. База для решения сложных задач 2 части ЕГЭ.

Как в евклидовой геометрии точка и прямая — главные элементы теории плоскостей, так и параллелограмм является одной из ключевых фигур выпуклых четырехугольников. Из него, как нитки из клубка, втекают понятия «прямоугольника», «квадрата», «ромба» и других геометрических величин.

Вконтакте

Определение параллелограмма

Выпуклый четырехугольник, состоящий из отрезков, каждая пара из которых параллельна, известен в геометрии как параллелограмм.

Как выглядит классический параллелограмм изображает четырехугольник ABCD. Стороны называются основаниями (AB, BC, CD и AD), перпендикуляр, проведенный из любой вершины на противоположную этой вершине сторону, — высотой (BE и BF), линии AC и BD — диагоналями.

Внимание! Квадрат, ромб и прямоугольник — это частные случаи параллелограмма.

Стороны и углы: особенности соотношения

Ключевые свойства, по большому счету, предопределены самим обозначением, их доказывает теорема. Эти характеристики следующие:

1. Стороны, которые являются противоположными, — попарно одинаковые.
2. Углы, расположенные противоположно друг другу — попарно равны.

Доказательство: рассмотрим ∆ABC и ∆ADC, которые получаются вследствие разделения четырехугольника ABCD прямой AC. ∠BCA=∠CAD и ∠BAC=∠ACD, поскольку AC для них общая (вертикальные углы для BC||AD и AB||CD, соответственно). Из этого следует: ∆ABC = ∆ADC (второй признак равенства треугольников).

Отрезки AB и BC в ∆ABC попарно соответствуют линиям CD и AD в ∆ADC, что означает их тождество: AB = CD, BC = AD. Таким образом, ∠B соответствует ∠D и они равны. Так как ∠A=∠BAC+∠CAD, ∠C=∠BCA+∠ACD, которые так же попарно одинаковые, то ∠A = ∠C. Свойство доказано.

Характеристики диагоналей фигуры

Основной признакэтих линий параллелограмма: точка пересечения разделяет их пополам.

Доказательство: пусть т. Е — это точка пересечения диагоналей AC и BD фигуры ABCD. Они образуют два соизмеримых треугольника — ∆ABE и ∆CDE.

AB=CD, так как они противоположные. Согласно прямых и секущей, ∠ABE = ∠CDE и ∠BAE = ∠DCE.

По второму признаку равенства ∆ABE = ∆CDE. Это означает, что элементы ∆ABE и ∆CDE: AE = CE, BE = DE и при этом они соразмерные части AC и BD. Свойство доказано.

Особенности смежных углов

У смежных сторон сумма углов равна 180°, поскольку они лежат по одну сторону параллельных линий и секущей. Для четырехугольника ABCD:

∠A+∠B=∠C+∠D=∠A+∠D=∠B+∠C=180º

Свойства биссектрисы:

1. , опущенные на одну сторону, являются перпендикулярными;
2. противолежащие вершины имеют параллельные биссектрисы;
3. треугольник, полученный проведением биссектрисы, будет равнобедренным.

Определение характерных черт параллелограмма по теореме

Признаки этой фигуры вытекают из ее основной теоремы, которая гласит следующее: четырехугольник считается параллелограммомв том случае, если его диагонали пересекаются, а эта точка разделяет их на равные отрезки.

Доказательство: пусть в т. Е прямые AC и BD четырехугольника ABCD пересекаются. Так как ∠AED = ∠BEC, а AE+CE=AC BE+DE=BD, то ∆AED = ∆BEC (по первому признаку равенства треугольников). То есть ∠EAD = ∠ECB. Они также являются внутренними перекрестными углами секущей AC для прямых AD и BC. Таким образом, по определению параллельности — AD || BC. Аналогичное свойство линий BC и CD выводится также. Теорема доказана.

Вычисление площади фигуры

Площадь этой фигуры находится несколькими методами,одним из самых простых: умножения высоты и основания, к которому она проведена.

Доказательство: проведем перпендикуляры BE и CF из вершин B и C. ∆ABE и ∆DCF — равные, поскольку AB = CD и BE = CF. ABCD — равновеликий с прямоугольником EBCF, так как они состоят и соразмерных фигур: S ABE и S EBCD , а также S DCF и S EBCD . Из этого следует, что площадь этой геометрической фигуры находится так же как и прямоугольника:

S ABCD = S EBCF = BE×BC=BE×AD.

Для определения общей формулы площади параллелограмма обозначим высоту как hb, а сторону — b. Соответственно:

Другие способы нахождения площади

Вычисления площади через стороны параллелограмма и угол, который они образуют, — второй известный метод.

,

Sпр-ма — площадь;

a и b — его стороны

α — угол между отрезками a и b.

Этот способ практически основывается на первом, но в случае, если неизвестна. всегда отрезает прямоугольный треугольник, параметры которого находятся тригонометрическими тождествами, то есть . Преобразуя соотношение, получаем . В уравнении первого способа заменяем высоту этим произведением и получаем доказательство справедливости этой формулы.

Через диагонали параллелограмма и угол, который они создают при пересечении, также можно найти площадь.

Доказательство: AC и BD пересекаясь, образуют четыре треугольника: ABE, BEC, CDE и AED. Их сумма равна площади этого четырехугольника.

Площадь каждого из этих ∆ можно найти за выражением , где a=BE, b=AE, ∠γ =∠AEB. Поскольку , то в расчетах используется единое значение синуса. То есть . Поскольку AE+CE=AC= d 1 и BE+DE=BD= d 2 , формула площади сводится до:

.

Применение в векторной алгебре

Особенности составляющих частей этого четырехугольника нашли применение в векторной алгебре, а именно: сложении двух векторов. Правило параллелограмма утверждает, что если заданные векторы и не коллинеарны, то их сумма будет равна диагонали этой фигуры, основания которой соответствуют этим векторам.

Доказательство: из произвольно выбранного начала — т. о. — строим векторы и . Далее строим параллелограмм ОАСВ, где отрезки OA и OB — стороны. Таким образом, ОС лежит на векторе или сумме .

Формулы для вычисления параметров параллелограмма

Тождества приведены при следующих условиях:

1. a и b, α — стороны и угол между ними;
2. d 1 и d 2 , γ — диагонали и в точке их пересечения;
3. h a и h b — высоты, опущенные на стороны a и b;

ПараметрФормулаНахождение сторонпо диагоналям и косинусу угла между ними

по диагоналям и стороне

через высоту и противоположную вершинуНахождение длины диагоналейпо сторонам и величине вершины между ними