திசையன்களின் அமைப்பின் நேரியல் சார்பு. கோலினியர் திசையன்கள்

திசையன் அமைப்பு என்று அழைக்கப்படுகிறது நேரியல் சார்ந்தது, குறைந்தபட்சம் ஒன்று பூஜ்ஜியத்திலிருந்து வேறுபட்ட எண்கள் இருந்தால், சமத்துவம் https://pandia.ru/text/78/624/images/image004_77.gif" width="57" height="24 src= " >.

இந்த சமத்துவம் அனைத்தும் இருக்கும் போது மட்டுமே திருப்தி அடைந்தால், திசையன்களின் அமைப்பு அழைக்கப்படுகிறது நேரியல் சார்பற்றது.

தேற்றம்.திசையன் அமைப்பு செய்யும் நேரியல் சார்ந்ததுஅதன் திசையன்களில் குறைந்தபட்சம் ஒன்று மற்றவற்றின் நேரியல் கலவையாக இருந்தால் மட்டுமே.

எடுத்துக்காட்டு 1.பல்லுறுப்புக்கோவை பல்லுறுப்புக்கோவைகளின் நேரியல் சேர்க்கையாகும் https://pandia.ru/text/78/624/images/image010_46.gif" width="88 height=24" height="24"> பல்லுறுப்புக்கோவை https: //pandia.ru/text/78/624/images/image012_44.gif" width="129" height="24">.

எடுத்துக்காட்டு 2.மேட்ரிக்ஸ் அமைப்பு, , https://pandia.ru/text/78/624/images/image016_37.gif" width="51" height="48 src="> நேரியல் சார்புடையது, ஏனெனில் ஒரு நேரியல் கலவையானது பூஜ்ஜிய அணி மட்டுமே https://pandia.ru/text/78/624/images/image019_27.gif" width="69" height="21">, , https://pandia.ru/text /78/624 /images/image022_26.gif" width="40" height="21"> நேரியல் சார்ந்தது.

தீர்வு.

இந்த திசையன்களின் நேரியல் கலவையை உருவாக்குவோம் https://pandia.ru/text/78/624/images/image023_29.gif" width="97" height="24">=0..gif" width="360" உயரம்="22">.

சம திசையன்களின் அதே ஆயங்களைச் சமன் செய்தால், https://pandia.ru/text/78/624/images/image027_24.gif" width="289" height="69">ஐப் பெறுகிறோம்

இறுதியாக நாம் பெறுகிறோம்

மற்றும்

கணினி ஒரு தனித்துவமான அற்பமான தீர்வைக் கொண்டுள்ளது, எனவே இந்த திசையன்களின் நேரியல் கலவையானது அனைத்து குணகங்களும் பூஜ்ஜியத்திற்கு சமமாக இருக்கும்போது மட்டுமே பூஜ்ஜியத்திற்கு சமமாக இருக்கும். எனவே, திசையன்களின் இந்த அமைப்பு நேரியல் சார்பற்றது.

எடுத்துக்காட்டு 4.திசையன்கள் நேரியல் சார்பற்றவை. திசையன் அமைப்புகள் எப்படி இருக்கும்?

a);

b).?

தீர்வு.

a)நேரியல் கலவையை உருவாக்கி அதை பூஜ்ஜியத்திற்கு சமன் செய்வோம்

நேரியல் இடத்தில் திசையன்களுடன் செயல்பாடுகளின் பண்புகளைப் பயன்படுத்தி, வடிவத்தில் கடைசி சமத்துவத்தை மீண்டும் எழுதுகிறோம்

திசையன்கள் நேரியல் சார்பற்றதாக இருப்பதால், இல் உள்ள குணகங்கள் பூஜ்ஜியத்திற்கு சமமாக இருக்க வேண்டும், அதாவது..gif" width="12" height="23 src=">

இதன் விளைவாக சமன்பாடுகளின் அமைப்பு ஒரு தனித்துவமான அற்பமான தீர்வைக் கொண்டுள்ளது .

சமத்துவம் இருந்து (*) https://pandia.ru/text/78/624/images/image031_26.gif" width="115 height=20" height="20"> - நேர்கோட்டுச் சார்பற்ற போது மட்டுமே செயல்படுத்தப்படும்;

b).சமத்துவத்தை உருவாக்குவோம் https://pandia.ru/text/78/624/images/image039_17.gif" width="265" height="24 src="> (**)

இதேபோன்ற காரணத்தைப் பயன்படுத்துவதன் மூலம், நாங்கள் பெறுகிறோம்

காஸ் முறை மூலம் சமன்பாடுகளின் அமைப்பைத் தீர்ப்பது, நாம் பெறுகிறோம்

அல்லது

பிந்தைய அமைப்பில் எண்ணற்ற தீர்வுகள் உள்ளன https://pandia.ru/text/78/624/images/image044_14.gif" width="149" height="24 src=">. எனவே, இல்லாதது உள்ளது சமத்துவத்தை வைத்திருக்கும் குணகங்களின் பூஜ்ஜிய தொகுப்பு (**) . எனவே, திசையன்களின் அமைப்பு - நேரியல் சார்ந்தது.

எடுத்துக்காட்டு 5திசையன்களின் அமைப்பு நேரியல் சார்புடையது, மேலும் திசையன்களின் அமைப்பு நேரியல் சார்ந்தது..gif" width="80" height="24">.gif" width="149 height=24" height="24"> (***)

சமத்துவத்தில் (***) . உண்மையில், இல், அமைப்பு நேரியல் சார்ந்ததாக இருக்கும்.

உறவில் இருந்து (***) நாம் பெறுகிறோம் அல்லது குறிப்போம் .

நாம் பெறுகிறோம்

க்கான பணிகள் சுதந்திரமான முடிவு(பார்வையில்)

1. பூஜ்ஜிய திசையன் கொண்ட அமைப்பு நேரியல் சார்ந்தது.

2. ஒரு திசையன் கொண்ட அமைப்பு ஏ, நேரியல் சார்ந்து இருந்தால் மட்டுமே a=0.

3. இரண்டு திசையன்களைக் கொண்ட அமைப்பு, திசையன்கள் விகிதாசாரமாக இருந்தால் மட்டுமே நேரியல் சார்ந்து இருக்கும் (அதாவது, அவற்றில் ஒன்று எண்ணால் பெருக்குவதன் மூலம் மற்றொன்றிலிருந்து பெறப்படுகிறது).

4. நீங்கள் ஒரு திசையனை ஒரு நேர்கோட்டு சார்ந்த அமைப்பில் சேர்த்தால், நீங்கள் ஒரு நேர்கோட்டு சார்ந்த அமைப்பைப் பெறுவீர்கள்.

5. ஒரு திசையன் ஒரு நேரியல் சார்பற்ற அமைப்பிலிருந்து அகற்றப்பட்டால், அதன் விளைவாக வரும் திசையன்களின் அமைப்பு நேரியல் சார்பற்றதாக இருக்கும்.

6. அமைப்பு என்றால் எஸ்நேரியல் சார்புடையது, ஆனால் ஒரு திசையன் சேர்க்கும் போது நேரியல் சார்ந்தது பி, பின்னர் திசையன் பிகணினி திசையன்கள் மூலம் நேர்கோட்டில் வெளிப்படுத்தப்படுகிறது எஸ்.

c)மெட்ரிக்குகளின் அமைப்பு, , இரண்டாவது வரிசை மெட்ரிக்குகளின் இடத்தில்.

10. திசையன்களின் அமைப்பை விடுங்கள் ஒரு,b,cதிசையன் இடம் நேரியல் சார்பற்றது. பின்வரும் திசையன் அமைப்புகளின் நேரியல் சுதந்திரத்தை நிரூபிக்கவும்:

a)a+b, b, c.

b).a+https://pandia.ru/text/78/624/images/image062_13.gif" width="15" height="19">–தன்னிச்சையான எண்

c)a+b, a+c, b+c.

11. விடுங்கள் ஒரு,b,c- ஒரு முக்கோணத்தை உருவாக்கக்கூடிய விமானத்தில் மூன்று திசையன்கள். இந்த திசையன்கள் நேரியல் சார்ந்து இருக்குமா?

12. இரண்டு திசையன்கள் கொடுக்கப்பட்டுள்ளன a1=(1, 2, 3, 4),a2=(0, 0, 0, 1). மேலும் இரண்டு நான்கு பரிமாண திசையன்களைக் கண்டறியவும் a3 மற்றும்a4அதனால் அமைப்பு a1,a2,a3,a4நேரியல் சுதந்திரமாக இருந்தது .

திசையன்கள், அவற்றின் பண்புகள் மற்றும் அவற்றுடன் செயல்கள்

திசையன்கள், திசையன்களுடன் செயல்கள், நேரியல் திசையன் இடம்.

திசையன்கள் என்பது ஒரு வரையறுக்கப்பட்ட உண்மையான எண்களின் வரிசைப்படுத்தப்பட்ட தொகுப்பாகும்.

செயல்கள்: 1.வெக்டரை எண்ணால் பெருக்குதல்: lambda*vector x=(lamda*x 1, lambda*x 2 ... lambda*x n).(3.4, 0, 7)*3=(9, 12,0.21)

2. திசையன்களைச் சேர்த்தல் (அதே திசையன் இடத்திற்குச் சொந்தமானது) திசையன் x + திசையன் y = (x 1 + y 1, x 2 + y 2, ... x n + y n,)

3. திசையன் 0=(0,0...0)---n E n – n-பரிமாண (நேரியல் வெளி) திசையன் x + திசையன் 0 = திசையன் x

தேற்றம். n திசையன்களின் அமைப்பு, ஒரு n-பரிமாண நேரியல் வெளி, நேரியல் சார்ந்ததாக இருக்க, திசையன்களில் ஒன்று மற்றவற்றின் நேரியல் கலவையாக இருப்பது அவசியம் மற்றும் போதுமானது.

தேற்றம். நிகழ்வுகளின் n-பரிமாண நேரியல் வெளியின் n+ 1வது திசையன்களின் எந்த தொகுப்பும். நேரியல் சார்ந்தது.

திசையன்களின் கூட்டல், எண்களால் திசையன்களை பெருக்குதல். திசையன்களின் கழித்தல்.

இரண்டு திசையன்களின் கூட்டுத்தொகை திசையன் தொடக்கத்தில் இருந்து திசையன் இறுதி வரை இயக்கப்பட்ட ஒரு திசையன் ஆகும், தொடக்கமானது திசையன் முடிவோடு ஒத்துப்போகிறது. வெக்டார்களை அடிப்படை அலகு திசையன்களில் அவற்றின் விரிவாக்கங்களால் கொடுக்கப்பட்டால், திசையன்களைச் சேர்க்கும்போது, ​​அவற்றுடன் தொடர்புடைய ஆயத்தொகுப்புகள் சேர்க்கப்படும்.

கார்ட்டீசியன் ஒருங்கிணைப்பு அமைப்பின் உதாரணத்தைப் பயன்படுத்தி இதைக் கருத்தில் கொள்வோம். விடுங்கள்

அதைக் காட்டுவோம்

படம் 3 இல் இருந்து அது தெளிவாகிறது

பலகோண விதியைப் பயன்படுத்தி எந்த வரையறுக்கப்பட்ட திசையன்களின் கூட்டுத்தொகையைக் காணலாம் (படம். 4): வரையறுக்கப்பட்ட எண்ணிக்கையிலான திசையன்களின் கூட்டுத்தொகையை உருவாக்க, ஒவ்வொரு அடுத்தடுத்த திசையனின் தொடக்கத்தையும் முந்தைய ஒன்றின் முடிவுடன் இணைத்தால் போதும். முதல் திசையனின் தொடக்கத்தையும் கடைசியின் முடிவுடன் இணைக்கும் திசையன் ஒன்றை உருவாக்கவும்.

திசையன் கூட்டல் செயல்பாட்டின் பண்புகள்:

இந்த வெளிப்பாடுகளில் m, n என்பது எண்கள்.

திசையன்களுக்கு இடையே உள்ள வேறுபாடு திசையன் எனப்படும்.

இதனால், திசையன்களைக் கழித்தல் செயல்பாடு கூட்டல் செயல்பாட்டால் மாற்றப்படுகிறது

புள்ளி A (x1, y1, z1) இல் தொடக்கத்திலும் முடிவிலும் இருக்கும் ஒரு திசையன் புள்ளி A இன் ஆரம் வெக்டார் என்று அழைக்கப்படுகிறது மற்றும் வெறுமனே குறிக்கப்படுகிறது. அதன் ஆயத்தொலைவுகள் புள்ளி A இன் ஆயத்தொலைவுகளுடன் ஒத்துப்போவதால், அலகு திசையன்களில் அதன் விரிவாக்கம் வடிவம் கொண்டது

புள்ளி A(x1, y1, z1) இல் தொடங்கி B(x2, y2, z2) புள்ளியில் முடிவடையும் ஒரு திசையன் இவ்வாறு எழுதலாம்

இதில் r 2 என்பது புள்ளி B இன் ஆரம் திசையன்; r 1 - புள்ளி A இன் ஆரம் திசையன்.

எனவே, அலகு திசையன்களில் திசையன் விரிவாக்கம் வடிவம் உள்ளது

அதன் நீளம் புள்ளிகள் A மற்றும் B இடையே உள்ள தூரத்திற்கு சமம்

பெருக்கல்

எனவே விமானச் சிக்கலில், ஒரு வெக்டரின் பலன் a = (ax; ay) மூலம் b என்ற எண்ணின் மூலம் சூத்திரத்தால் கண்டறியப்படுகிறது.

a b = (ax b; ay b)

எடுத்துக்காட்டு 1. திசையன் a = (1; 2) இன் 3 ஆல் பெருக்கத்தைக் கண்டறியவும்.

3 a = (3 1; 3 2) = (3; 6)

எனவே, ஒரு இடஞ்சார்ந்த பிரச்சனையில், திசையன் a = (ax; ay; az) எண்ணின் மூலம் b என்ற எண்ணின் பலன் சூத்திரத்தால் கண்டறியப்படுகிறது.

a b = (ax b; ay b; az b)

எடுத்துக்காட்டு 1. திசையன் a = (1; 2; -5) இன் பெருளை 2 ஆல் கண்டறியவும்.

2 a = (2 1; 2 2; 2 (-5)) = (2; 4; -10)

திசையன்களின் புள்ளி தயாரிப்பு மற்றும் திசையன்களுக்கு இடையே உள்ள கோணம் மற்றும் ; ஒன்று இருந்தால், பிறகு

ஸ்கேலர் தயாரிப்பின் வரையறையிலிருந்து அது பின்வருமாறு

உதாரணமாக, வெக்டரின் திசையில் திசையன் ப்ரொஜெக்ஷனின் அளவு.

ஸ்கேலார் ஸ்கொயர் வெக்டார்:

டாட் தயாரிப்பின் பண்புகள்:

ஆயத்தொகுப்புகளில் புள்ளி தயாரிப்பு

என்றால் அந்த

திசையன்களுக்கு இடையிலான கோணம்

திசையன்களுக்கு இடையிலான கோணம் - இந்த திசையன்களின் திசைகளுக்கு இடையே உள்ள கோணம் (சிறிய கோணம்).

குறுக்கு தயாரிப்பு (இரண்டு திசையன்களின் குறுக்கு தயாரிப்பு.) -இது இரண்டு காரணிகளிலிருந்து கட்டமைக்கப்பட்ட ஒரு விமானத்திற்கு செங்குத்தாக இருக்கும் ஒரு சூடோவெக்டராகும், இது முப்பரிமாண யூக்ளிடியன் இடத்தில் உள்ள திசையன்களின் மீது "வெக்டார் பெருக்கல்" என்ற பைனரி செயல்பாட்டின் விளைவாகும். தயாரிப்பு பரிமாற்றம் அல்லது துணை இல்லை (இது எதிர்மாற்றம்) மற்றும் திசையன்களின் புள்ளி உற்பத்தியில் இருந்து வேறுபட்டது. பல பொறியியல் மற்றும் இயற்பியல் சிக்கல்களில், நீங்கள் ஏற்கனவே உள்ள இரண்டுவற்றுக்கு செங்குத்தாக ஒரு திசையனை உருவாக்க முடியும் - திசையன் தயாரிப்பு இந்த வாய்ப்பை வழங்குகிறது. குறுக்கு தயாரிப்பு திசையன்களின் செங்குத்தாக "அளவிடுவதற்கு" பயனுள்ளதாக இருக்கும் - நீளம் திசையன் தயாரிப்புஇரண்டு திசையன்கள் செங்குத்தாக இருந்தால் அவற்றின் நீளத்தின் பெருக்கத்திற்குச் சமமாக இருக்கும், மேலும் திசையன்கள் இணையாகவோ அல்லது இணையாகவோ இருந்தால் பூஜ்ஜியமாகக் குறையும்.

குறுக்கு தயாரிப்பு முப்பரிமாண மற்றும் ஏழு பரிமாண இடைவெளிகளில் மட்டுமே வரையறுக்கப்படுகிறது. ஒரு திசையன் உற்பத்தியின் முடிவு, ஒரு அளவிடல் தயாரிப்பு போன்றது, யூக்ளிடியன் இடத்தின் அளவீட்டைப் பொறுத்தது.

முப்பரிமாண செவ்வக ஒருங்கிணைப்பு அமைப்பில் உள்ள ஒருங்கிணைப்புகளிலிருந்து அளவிடுதல் தயாரிப்பு திசையன்களைக் கணக்கிடுவதற்கான சூத்திரத்தைப் போலன்றி, குறுக்கு தயாரிப்புக்கான சூத்திரம் செவ்வக ஒருங்கிணைப்பு அமைப்பின் நோக்குநிலையைப் பொறுத்தது அல்லது வேறுவிதமாகக் கூறினால், அதன் "சிராலிட்டி"

திசையன்களின் கூட்டுத்தன்மை.

இரண்டு பூஜ்ஜியமற்ற (0க்கு சமமாக இல்லை) திசையன்கள் இணையான கோடுகளில் அல்லது ஒரே கோட்டில் இருந்தால் அவை கோலினியர் என்று அழைக்கப்படுகின்றன. ஏற்றுக்கொள்ளக்கூடிய, ஆனால் பரிந்துரைக்கப்படாத, இணையான "இணை" திசையன்கள். கோலினியர் திசையன்கள் ஒரே மாதிரியாக இயக்கப்படலாம் ("கோடிரெக்ஷனல்") அல்லது எதிர் திசையில் (பிந்தைய வழக்கில் அவை சில நேரங்களில் "எதிர்கோலினியர்" அல்லது "ஆன்டிபராலல்" என்று அழைக்கப்படுகின்றன).

திசையன்களின் கலப்பு தயாரிப்பு( a, b, c)- திசையன் a இன் அளவிடல் தயாரிப்பு மற்றும் b மற்றும் c திசையன்களின் திசையன் தயாரிப்பு:

(a,b,c)=a ⋅(b ×c)

சில நேரங்களில் மூன்று என்று அழைக்கப்படுகிறது அளவிடல் தயாரிப்புதிசையன்கள், பெரும்பாலும் இதன் விளைவாக ஒரு ஸ்கேலர் (இன்னும் துல்லியமாக, ஒரு சூடோஸ்கேலர்) காரணமாக இருக்கலாம்.

வடிவியல் பொருள்: கலப்புப் பொருளின் மாடுலஸ், வெக்டார்களால் உருவாகும் பேரலலெலிபிப்பின் தொகுதிக்கு எண்ரீதியாக சமம். (a,b,c) .

பண்புகள்

கலப்பு துண்டுஅதன் அனைத்து வாதங்களையும் பொறுத்து வளைவு-சமச்சீர்: அதாவது. e. ஏதேனும் இரண்டு காரணிகளை மறுசீரமைப்பது தயாரிப்பின் அடையாளத்தை மாற்றுகிறது. சரியான கார்ட்டீசியன் ஒருங்கிணைப்பு அமைப்பில் உள்ள கலப்பு தயாரிப்பு (ஒரு ஆர்த்தோநார்மல் அடிப்படையில்) வெக்டார்களைக் கொண்ட மேட்ரிக்ஸின் நிர்ணயம் மற்றும்:

இடது கார்ட்டீசியன் ஒருங்கிணைப்பு அமைப்பில் உள்ள கலப்பு தயாரிப்பு (ஒரு ஆர்த்தோநார்மல் அடிப்படையில்) திசையன்களால் ஆன மேட்ரிக்ஸின் நிர்ணயிப்பிற்கு சமம் மற்றும் கழித்தல் அடையாளத்துடன் எடுக்கப்பட்டது:

குறிப்பாக,

எந்த இரண்டு திசையன்களும் இணையாக இருந்தால், எந்த மூன்றாவது திசையனுடனும் அவை பூஜ்ஜியத்திற்கு சமமான கலப்பு உற்பத்தியை உருவாக்குகின்றன.

மூன்று திசையன்கள் நேரியல் சார்ந்து இருந்தால் (அதாவது, கோப்லனர், ஒரே விமானத்தில் கிடக்கிறது), பின்னர் அவற்றின் கலப்பு தயாரிப்பு பூஜ்ஜியத்திற்கு சமம்.

வடிவியல் பொருள் - கலப்புத் தயாரிப்பு என்பது வெக்டார்களால் உருவாக்கப்பட்ட இணைக் குழாய்களின் (படத்தைப் பார்க்கவும்) தொகுதிக்கு முழுமையான மதிப்பில் சமமாக இருக்கும். இந்த மூன்று திசையன்கள் வலது கை அல்லது இடது கை என்பதைச் சார்ந்தது.

திசையன்களின் கோப்லானாரிட்டி.

மூன்று திசையன்கள் (அல்லது பெரிய எண்) பொதுவான தோற்றத்திற்குக் குறைக்கப்பட்டு, ஒரே விமானத்தில் இருந்தால், அவை கோப்லனர் என்று அழைக்கப்படுகின்றன

கோப்லானாரிட்டியின் பண்புகள்

மூன்று திசையன்களில் குறைந்தபட்சம் ஒன்று பூஜ்ஜியமாக இருந்தால், மூன்று திசையன்களும் கோப்லனர் என்று கருதப்படுகின்றன.

ஒரு ஜோடி கோலினியர் திசையன்களைக் கொண்ட மூன்று திசையன்கள் கோப்லனர் ஆகும்.

கோப்லனர் வெக்டர்களின் கலப்பு தயாரிப்பு. இது மூன்று திசையன்களின் கோப்லானாரிட்டிக்கான அளவுகோலாகும்.

கோப்லனர் திசையன்கள் நேரியல் சார்ந்தது. கோப்லானாரிட்டிக்கு இதுவும் ஒரு அளவுகோலாகும்.

3-பரிமாண இடத்தில், 3 கோப்லானர் அல்லாத திசையன்கள் ஒரு அடிப்படையை உருவாக்குகின்றன

நேரியல் சார்ந்த மற்றும் நேரியல் சார்பற்ற திசையன்கள்.

நேரியல் சார்ந்த மற்றும் சுயாதீன திசையன் அமைப்புகள்.வரையறை. திசையன் அமைப்பு என்று அழைக்கப்படுகிறது நேரியல் சார்ந்தது, பூஜ்ஜிய வெக்டருக்குச் சமமான இந்தத் திசையன்களின் குறைந்தபட்சம் ஒரு அற்பமான நேரியல் சேர்க்கையாவது இருந்தால். இல்லையெனில், அதாவது. கொடுக்கப்பட்ட திசையன்களின் அற்பமான நேரியல் கலவை மட்டுமே பூஜ்ய திசையன் சமமாக இருந்தால், திசையன்கள் அழைக்கப்படுகின்றன நேரியல் சார்பற்றது.

தேற்றம் (நேரியல் சார்பு அளவுகோல்). ஒரு நேரியல் இடத்தில் உள்ள திசையன்களின் அமைப்பு நேரியல் சார்ந்ததாக இருக்க, இந்த திசையன்களில் குறைந்தபட்சம் ஒன்று மற்றவற்றின் நேரியல் கலவையாக இருப்பது அவசியம் மற்றும் போதுமானது.

1) திசையன்களில் குறைந்தது ஒரு பூஜ்ஜிய திசையன் இருந்தால், திசையன்களின் முழு அமைப்பும் நேரியல் சார்ந்தது.

உண்மையில், எடுத்துக்காட்டாக, , எனில் , அனுமானித்தால் , நம்மிடம் ஒரு அற்பமான நேரியல் கலவை உள்ளது .▲

2) திசையன்களில் சில நேர்கோட்டு சார்ந்த அமைப்பை உருவாக்கினால், முழு அமைப்பும் நேரியல் சார்ந்து இருக்கும்.

உண்மையில், திசையன்கள், , நேரியல் சார்ந்து இருக்கட்டும். பூஜ்ஜிய வெக்டருக்கு சமமான அற்பமான நேரியல் சேர்க்கை உள்ளது என்பதே இதன் பொருள். ஆனால் பின்னர், அனுமானித்து , பூஜ்ஜிய வெக்டருக்கு சமமான அற்பமான நேரியல் கலவையையும் நாங்கள் பெறுகிறோம்.

2. அடிப்படை மற்றும் பரிமாணம். வரையறை. நேரியல் சார்பற்ற திசையன்களின் அமைப்பு திசையன் வெளி என்று அழைக்கப்படுகிறது அடிப்படையில்இந்த இடத்திலிருந்து ஏதேனும் திசையன் இந்த அமைப்பின் திசையன்களின் நேரியல் கலவையாக குறிப்பிடப்பட்டால், அதாவது. ஒவ்வொரு திசையன்களுக்கும் உண்மையான எண்கள் உள்ளன இந்த சமத்துவம் என்று அழைக்கப்படுகிறது திசையன் சிதைவுஅடிப்படை மற்றும் எண்களின் படி அழைக்கப்படுகின்றன அடிப்படையுடன் தொடர்புடைய திசையன் ஆயத்தொகுப்புகள்(அல்லது அடிப்படையில்) .

தேற்றம் (அடிப்படையில் விரிவாக்கத்தின் தனித்தன்மையில்). விண்வெளியில் உள்ள ஒவ்வொரு திசையன்களையும் ஒரு அடிப்படையாக விரிவுபடுத்தலாம் ஒரே வழியில், அதாவது. அடிப்படையில் ஒவ்வொரு திசையன் ஆய சந்தேகத்திற்கு இடமின்றி தீர்மானிக்கப்படுகிறது.

திசையன்களின் அமைப்பு நேரியல் சார்ந்ததா என்பதைச் சரிபார்க்க, இந்த திசையன்களின் நேரியல் கலவையை உருவாக்குவது அவசியம், மேலும் குறைந்தபட்சம் ஒரு குணகம் பூஜ்ஜியத்திற்கு சமமாக இருந்தால் அது பூஜ்ஜியமாக இருக்க முடியுமா என்பதைச் சரிபார்க்கவும்.

வழக்கு 1. திசையன்களின் அமைப்பு திசையன்களால் வழங்கப்படுகிறது

நேரியல் கலவையை உருவாக்குதல்

சமன்பாடுகளின் ஒரே மாதிரியான அமைப்பைப் பெற்றுள்ளோம். பூஜ்ஜியம் அல்லாத தீர்வு இருந்தால், தீர்மானிப்பான் பூஜ்ஜியத்திற்கு சமமாக இருக்க வேண்டும். ஒரு தீர்மானியை உருவாக்கி அதன் மதிப்பைக் கண்டுபிடிப்போம்.

தீர்மானிப்பான் பூஜ்ஜியமாகும், எனவே திசையன்கள் நேரியல் சார்ந்து இருக்கும்.

வழக்கு 2. திசையன்களின் அமைப்பு பகுப்பாய்வு செயல்பாடுகளால் வரையறுக்கப்படுகிறது:

a)
, அடையாளம் உண்மையாக இருந்தால், அமைப்பு நேரியல் சார்ந்தது.

நேரியல் கலவையை உருவாக்குவோம்.

இந்த வெளிப்பாடு பூஜ்ஜியத்திற்கு சமமான a, b, c (குறைந்தபட்சம் ஒன்று பூஜ்ஜியத்திற்கு சமமாக இல்லை) உள்ளதா என்பதைச் சரிபார்க்க வேண்டியது அவசியம்.

ஹைபர்போலிக் செயல்பாடுகளை எழுதுவோம்

,
, பிறகு

பின்னர் திசையன்களின் நேரியல் கலவை வடிவம் எடுக்கும்:

எங்கே
, எடுத்துக் கொள்ளுங்கள், எடுத்துக்காட்டாக, நேரியல் கலவை பூஜ்ஜியமாகும், எனவே, கணினி நேரியல் சார்ந்தது.

பதில்: அமைப்பு நேரியல் சார்ந்தது.

b)
, நேரியல் கலவையை உருவாக்குவோம்

திசையன்களின் நேரியல் கலவையானது x இன் எந்த மதிப்புக்கும் பூஜ்ஜியத்திற்கு சமமாக இருக்க வேண்டும்.

சிறப்பு வழக்குகளை சரிபார்ப்போம்.

அனைத்து குணகங்களும் பூஜ்ஜியத்திற்கு சமமாக இருந்தால் மட்டுமே திசையன்களின் நேரியல் கலவை பூஜ்ஜியத்திற்கு சமம்.

எனவே, அமைப்பு நேரியல் சார்பற்றது.

பதில்: அமைப்பு நேரியல் சார்பற்றது.

5.3 சில அடிப்படைகளைக் கண்டறிந்து, நேரியல் தீர்வு இடத்தின் பரிமாணத்தைத் தீர்மானிக்கவும்.

காசியன் முறையைப் பயன்படுத்தி நீட்டிக்கப்பட்ட மேட்ரிக்ஸை உருவாக்கி அதை ட்ரேப்சாய்டு வடிவத்திற்குக் குறைப்போம்.

சில அடிப்படைகளைப் பெற, தன்னிச்சையான மதிப்புகளை மாற்றுவோம்:

மீதமுள்ள ஆயங்களைப் பெறுவோம்

பதில்:

5.4 அடிப்படையில் கொடுக்கப்பட்டிருந்தால், திசையன் X இன் ஆயத்தொலைவுகளை அடிப்படையில் கண்டறியவும்.

ஒரு புதிய அடிப்படையில் திசையன் ஒருங்கிணைப்புகளைக் கண்டறிவது சமன்பாடுகளின் அமைப்பைத் தீர்ப்பதில் இறங்குகிறது

முறை 1. மாற்றம் மேட்ரிக்ஸைப் பயன்படுத்தி கண்டறிதல்

மாறுதல் மேட்ரிக்ஸை உருவாக்குவோம்

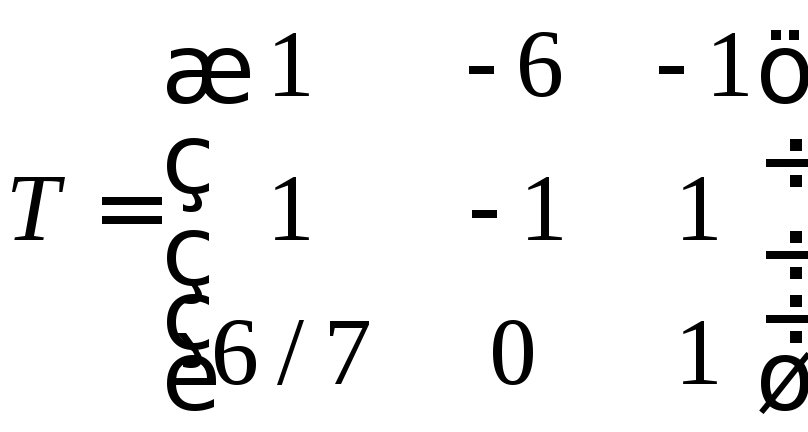
சூத்திரத்தைப் பயன்படுத்தி புதிய அடிப்படையில் வெக்டரைக் கண்டுபிடிப்போம்

தலைகீழ் மேட்ரிக்ஸைக் கண்டுபிடித்து பெருக்கலைச் செய்வோம்

,

முறை 2. சமன்பாடுகளின் அமைப்பை உருவாக்குவதன் மூலம் கண்டறிதல்.

அடிப்படை குணகங்களிலிருந்து அடிப்படை திசையன்களை உருவாக்குவோம்

,
,

புதிய அடிப்படையில் வெக்டரைக் கண்டறிவது வடிவம் கொண்டது

, எங்கே ஈஇது கொடுக்கப்பட்ட திசையன் எக்ஸ்.

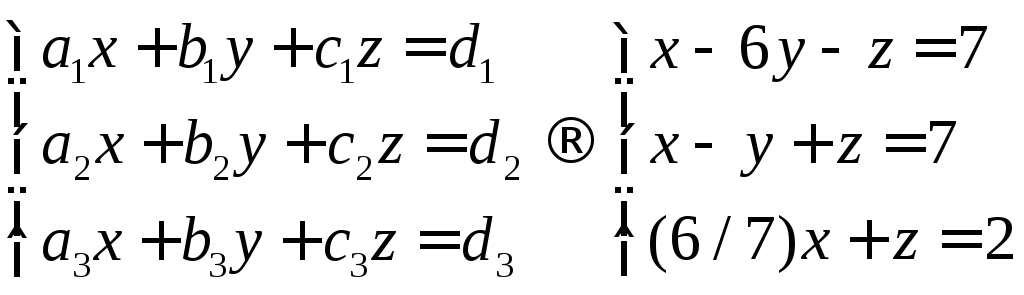
இதன் விளைவாக சமன்பாடு எந்த வகையிலும் தீர்க்கப்படலாம், பதில் ஒத்ததாக இருக்கும்.

பதில்: புதிய அடிப்படையில் திசையன்
.

5.5 x = என்பதை விடுங்கள் (எக்ஸ் 1 , எக்ஸ் 2 , எக்ஸ் 3 ) . பின்வரும் மாற்றங்கள் நேர்கோட்டில் உள்ளதா?

கொடுக்கப்பட்ட வெக்டார்களின் குணகங்களிலிருந்து நேரியல் ஆபரேட்டர்களின் மெட்ரிக்குகளை உருவாக்குவோம்.

ஒவ்வொரு லீனியர் ஆபரேட்டர் மேட்ரிக்ஸுக்கும் நேரியல் செயல்பாடுகளின் பண்பைச் சரிபார்ப்போம்.

மேட்ரிக்ஸைப் பெருக்கி இடது பக்கத்தைக் காண்கிறோம் ஏதிசையன்

கொடுக்கப்பட்ட வெக்டரை ஒரு அளவுகோலால் பெருக்குவதன் மூலம் வலது பக்கத்தைக் காண்கிறோம்
.

என்று பார்க்கிறோம்
இதன் பொருள் மாற்றம் நேரியல் அல்ல.

மற்ற திசையன்களை சரிபார்க்கலாம்.

, மாற்றம் நேரியல் அல்ல.

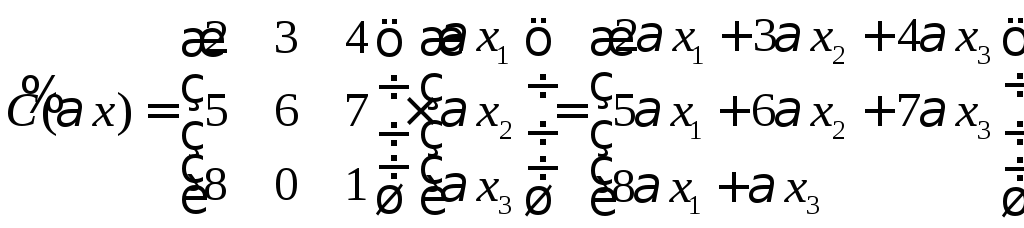
, மாற்றம் நேரியல்.

பதில்: ஓ- நேரியல் மாற்றம் அல்ல, இல்- நேரியல் அல்ல, Cx- நேரியல்.

குறிப்பு.கொடுக்கப்பட்ட திசையன்களை கவனமாகப் பார்ப்பதன் மூலம் இந்த பணியை நீங்கள் எளிதாக முடிக்கலாம். IN ஓஉறுப்புகள் இல்லாத சொற்கள் இருப்பதைக் காண்கிறோம் எக்ஸ், இது நேரியல் செயல்பாட்டின் விளைவாக பெற முடியவில்லை. IN இல்ஒரு உறுப்பு உள்ளது எக்ஸ்மூன்றாவது சக்திக்கு, இது ஒரு திசையன் மூலம் பெருக்குவதன் மூலம் பெற முடியாது எக்ஸ்.

5.6 கொடுக்கப்பட்டது எக்ஸ் = { எக்ஸ் 1 , எக்ஸ் 2 , எக்ஸ் 3 } , கோடாரி = { எக்ஸ் 2 – எக்ஸ் 3 , எக்ஸ் 1 , எக்ஸ் 1 + எக்ஸ் 3 } , Bx = { எக்ஸ் 2 , 2 எக்ஸ் 3 , எக்ஸ் 1 } . குறிப்பிட்ட செயல்பாட்டைச் செய்யவும்: ( ஏ ( பி – ஏ )) எக்ஸ் .

லீனியர் ஆபரேட்டர்களின் மெட்ரிக்குகளை எழுதுவோம்.

மெட்ரிக்குகளில் ஒரு ஆபரேஷன் செய்வோம்

இதன் விளைவாக வரும் மேட்ரிக்ஸை X ஆல் பெருக்கும்போது, ​​​​நாம் பெறுகிறோம்

பதில்:

இந்த கட்டுரையில் நாம் உள்ளடக்குவோம்:

• கோலினியர் வெக்டர்கள் என்றால் என்ன;
• திசையன்களின் கோலினரிட்டிக்கான நிபந்தனைகள் என்ன;
• கோலினியர் திசையன்களின் என்ன பண்புகள் உள்ளன;
• கோலினியர் வெக்டார்களின் நேரியல் சார்பு என்ன.

Yandex.RTB R-A-339285-1 வரையறை 1

கோலினியர் வெக்டர்கள் ஒரு கோட்டிற்கு இணையாக இருக்கும் அல்லது ஒரு கோட்டில் இருக்கும் திசையன்கள்.

எடுத்துக்காட்டு 1

திசையன்களின் இணைத்தன்மைக்கான நிபந்தனைகள்

பின்வரும் நிபந்தனைகளில் ஏதேனும் உண்மையாக இருந்தால் இரண்டு வெக்டார்களும் கோலினியர் ஆகும்:

• நிபந்தனை 1 . a = λ b போன்ற ஒரு எண் λ இருந்தால் திசையன்கள் a மற்றும் b ஆகியவை கோலினியர் ஆகும்;
• நிபந்தனை 2 . திசையன்கள் a மற்றும் b ஆகியவை சமமான ஒருங்கிணைப்பு விகிதங்களுடன் கோலினியர் ஆகும்:

a = (a 1 ; a 2), b = (b 1 ; b 2) ⇒ a ∥ b ⇔ a 1 b 1 = a 2 b 2

• நிபந்தனை 3 . குறுக்கு தயாரிப்பு மற்றும் பூஜ்ஜிய திசையன் சமமாக இருக்கும் போது திசையன்கள் a மற்றும் b ஆகியவை கோலினியர் ஆகும்:

a ∥ b ⇔ a, b = 0

குறிப்பு 1

நிபந்தனை 2 திசையன் ஒருங்கிணைப்புகளில் ஒன்று பூஜ்ஜியமாக இருந்தால் பொருந்தாது.

குறிப்பு 2

நிபந்தனை 3 விண்வெளியில் குறிப்பிடப்பட்டுள்ள திசையன்களுக்கு மட்டுமே பொருந்தும்.

திசையன்களின் கோலினரிட்டியை ஆய்வு செய்வதற்கான சிக்கல்களின் எடுத்துக்காட்டுகள்

எடுத்துக்காட்டு 1

ஒரு = (1; 3) மற்றும் b = (2; 1) ஆகிய வெக்டார்களை கோலினரிட்டிக்காக ஆராய்வோம்.

எப்படி தீர்ப்பது?

IN இந்த வழக்கில் 2வது கோலினியரிட்டி நிபந்தனையைப் பயன்படுத்துவது அவசியம். கொடுக்கப்பட்ட திசையன்களுக்கு இது போல் தெரிகிறது:

சமத்துவம் பொய்யானது. இதிலிருந்து நாம் a மற்றும் b திசையன்கள் கோலினியர் அல்ல என்று முடிவு செய்யலாம்.

பதில் : a | | பி

எடுத்துக்காட்டு 2

திசையன்கள் கோலினியராக இருப்பதற்கு, a = (1; 2) மற்றும் b = (- 1; m) இன் வெக்டரின் மதிப்பு என்ன?

எப்படி தீர்ப்பது?

இரண்டாவது கோலினியரிட்டி நிலையைப் பயன்படுத்தி, திசையன்கள் அவற்றின் ஆயத்தொலைவுகள் விகிதாசாரமாக இருந்தால் அவை கோலினியராக இருக்கும்:

இது m = - 2 என்பதைக் காட்டுகிறது.

பதில்: மீ = - 2 .

திசையன் அமைப்புகளின் நேரியல் சார்பு மற்றும் நேரியல் சுதந்திரத்திற்கான அளவுகோல்கள்

தேற்றம்

ஒரு திசையன் இடத்தில் உள்ள திசையன்களின் அமைப்பு நேரியல் சார்ந்தது, அமைப்பின் திசையன்களில் ஒன்றை இந்த அமைப்பின் மீதமுள்ள திசையன்களின் அடிப்படையில் வெளிப்படுத்த முடியும்.

ஆதாரம்

கணினி e 1 , e 2 , . . . , e n என்பது நேரியல் சார்ந்தது. பூஜ்ஜிய வெக்டருக்கு சமமான இந்த அமைப்பின் நேரியல் கலவையை எழுதுவோம்:

a 1 e 1 + a 2 e 2 + . . . + a n e n = 0

இதில் சேர்க்கை குணகங்களில் குறைந்தபட்சம் ஒன்று பூஜ்ஜியத்திற்கு சமமாக இருக்காது.

ஒரு k ≠ 0 k ∈ 1 , 2 , . . . , என்.

சமத்துவத்தின் இரு பக்கங்களையும் பூஜ்ஜியமற்ற குணகத்தால் பிரிக்கிறோம்:

a k - 1 (a k - 1 a 1) e 1 + (a k - 1 a k) e k + . . . + (a k - 1 a n) e n = 0

குறிப்போம்:

A k - 1 a m, இங்கு m ∈ 1 , 2 , . . . , k - 1 , k + 1 , n

இந்த வழக்கில்:

β 1 e 1 + . . . + β k - 1 e k - 1 + β k + 1 e k + 1 + . . . + β n e n = 0

அல்லது e k = (- β 1) e 1 + . . . + (- β k - 1) e k - 1 + (- β k + 1) e k + 1 + . . . + (- β n) e n

கணினியின் திசையன்களில் ஒன்று கணினியின் மற்ற அனைத்து திசையன்கள் மூலமாகவும் வெளிப்படுத்தப்படுகிறது. எது நிரூபிக்கப்பட வேண்டும் (முதலியன).

போதுமானது

கணினியின் மற்ற அனைத்து வெக்டர்கள் மூலம் திசையன்களில் ஒன்று நேரியல் முறையில் வெளிப்படுத்தப்படட்டும்:

e k = γ 1 e 1 + . . . + γ k - 1 e k - 1 + γ k + 1 e k + 1 + . . . + γ n e n

திசையன் e k ஐ இந்த சமத்துவத்தின் வலது பக்கத்திற்கு நகர்த்துகிறோம்:

0 = γ 1 இ 1 + . . . + γ k - 1 e k - 1 - e k + γ k + 1 e k + 1 + . . . + γ n e n

திசையன் e k இன் குணகம் - 1 ≠ 0 க்கு சமமாக இருப்பதால், திசையன்கள் e 1, e 2, அமைப்பு மூலம் பூஜ்ஜியத்தின் அற்பமான பிரதிநிதித்துவத்தைப் பெறுகிறோம். . . , e n , மற்றும் இது, திசையன்களின் இந்த அமைப்பு நேரியல் சார்ந்தது என்று அர்த்தம். எது நிரூபிக்கப்பட வேண்டும் (முதலியன).

விளைவு:

• திசையன்களின் அமைப்பு அதன் திசையன்கள் எதுவும் அமைப்பின் மற்ற அனைத்து திசையன்களின் அடிப்படையில் வெளிப்படுத்த முடியாதபோது நேரியல் சார்புடையதாக இருக்கும்.
• பூஜ்ஜிய திசையன் அல்லது இரண்டு சம திசையன்களைக் கொண்ட திசையன்களின் அமைப்பு நேரியல் சார்ந்தது.

நேரியல் சார்ந்த திசையன்களின் பண்புகள்

1. 2- மற்றும் 3-பரிமாண திசையன்களுக்கு, பின்வரும் நிபந்தனை பூர்த்தி செய்யப்படுகிறது: இரண்டு நேரியல் சார்ந்த திசையன்கள் கோலினியர். இரண்டு கோலினியர் திசையன்கள் நேரியல் சார்ந்து உள்ளன.
2. 3-பரிமாண திசையன்களுக்கு நிபந்தனை திருப்தி அளிக்கிறது: மூன்று நேரியல் சார்ந்த திசையன்கள்- கோப்ளனார். (3 கோப்லனர் திசையன்கள் நேரியல் சார்ந்தவை).
3. n-பரிமாண திசையன்களுக்கு, பின்வரும் நிபந்தனை பூர்த்தி செய்யப்படுகிறது: n + 1 திசையன்கள் எப்போதும் நேரியல் சார்ந்து இருக்கும்.

திசையன்களின் நேரியல் சார்பு அல்லது நேரியல் சுதந்திரம் சம்பந்தப்பட்ட சிக்கல்களைத் தீர்ப்பதற்கான எடுத்துக்காட்டுகள்

எடுத்துக்காட்டு 3

நேரியல் சுதந்திரத்திற்காக a = 3, 4, 5, b = - 3, 0, 5, c = 4, 4, 4, d = 3, 4, 0 ஆகிய திசையன்களை சரிபார்க்கலாம்.

தீர்வு. திசையன்களின் பரிமாணம் திசையன்களின் எண்ணிக்கையை விட குறைவாக இருப்பதால் திசையன்கள் நேரியல் சார்ந்து இருக்கும்.

எடுத்துக்காட்டு 4

நேரியல் சுதந்திரத்திற்காக a = 1, 1, 1, b = 1, 2, 0, c = 0, - 1, 1 ஆகிய திசையன்களை சரிபார்க்கலாம்.

தீர்வு. நேரியல் கலவை பூஜ்ஜிய வெக்டருக்கு சமமாக இருக்கும் குணகங்களின் மதிப்புகளைக் காண்கிறோம்:

x 1 a + x 2 b + x 3 c 1 = 0

திசையன் சமன்பாட்டை நேரியல் வடிவத்தில் எழுதுகிறோம்:

x 1 + x 2 = 0 x 1 + 2 x 2 - x 3 = 0 x 1 + x 3 = 0

காஸ் முறையைப் பயன்படுத்தி இந்த அமைப்பை நாங்கள் தீர்க்கிறோம்:

1 1 0 | 0 1 2 - 1 | 0 1 0 1 | 0 ~

2 வது வரியிலிருந்து 1 வது, 3 வது - 1 வது ஆகியவற்றைக் கழிக்கிறோம்:

~ 1 1 0 | 0 1 - 1 2 - 1 - 1 - 0 | 0 - 0 1 - 1 0 - 1 1 - 0 | 0 - 0 ~ 1 1 0 | 0 0 1 - 1 | 0 0 - 1 1 | 0 ~

1 வது வரியில் இருந்து நாம் 2 வது கழிக்கிறோம், 3 வது 2 வது சேர்க்கிறோம்:

~ 1 - 0 1 - 1 0 - (- 1) | 0 - 0 0 1 - 1 | 0 0 + 0 - 1 + 1 1 + (- 1) | 0 + 0 ~ 0 1 0 | 1 0 1 - 1 | 0 0 0 0 | 0

தீர்விலிருந்து, கணினியில் பல தீர்வுகள் உள்ளன. இதன் பொருள் x 1, x 2, x 3 போன்ற எண்களின் மதிப்புகளின் பூஜ்ஜியமற்ற சேர்க்கை உள்ளது, இதற்கு a, b, c இன் நேரியல் கலவை பூஜ்ஜிய திசையன் சமமாகும். எனவே, திசையன்கள் a, b, c நேரியல் சார்ந்தது.

உரையில் பிழையைக் கண்டால், அதை முன்னிலைப்படுத்தி Ctrl+Enter ஐ அழுத்தவும்

அ 1 = { 3, 5, 1 , 4 }, அ 2 = { –2, 1, -5 , -7 }, அ 3 = { -1, –2, 0, –1 }.

தீர்வு.தேடி வருகின்றனர் பொதுவான முடிவுசமன்பாடுகளின் அமைப்புகள்

அ 1 எக்ஸ் 1 + அ 2 எக்ஸ் 2 + அ 3 எக்ஸ் 3 = Θ

காஸ் முறை. இதைச் செய்ய, இந்த ஒரே மாதிரியான அமைப்பை ஒருங்கிணைப்புகளில் எழுதுகிறோம்:

சிஸ்டம் மேட்ரிக்ஸ்

அனுமதிக்கப்பட்ட அமைப்பு வடிவம் உள்ளது: (ஆர் ஏ = 2, n= 3). அமைப்பு ஒத்துழைப்பு மற்றும் நிச்சயமற்றது. அதன் பொதுவான தீர்வு ( எக்ஸ் 2 - இலவச மாறி): எக்ஸ் 3 = 13எக்ஸ் 2 ; 3எக்ஸ் 1 – 2எக்ஸ் 2 – 13எக்ஸ் 2 = 0 => எக்ஸ் 1 = 5எக்ஸ் 2 => எக்ஸ் o = . பூஜ்ஜியம் அல்லாத குறிப்பிட்ட தீர்வு இருப்பது, எடுத்துக்காட்டாக, திசையன்கள் என்பதைக் குறிக்கிறது அ 1 , அ 2 , அ 3 நேரியல் சார்ந்தது.

எடுத்துக்காட்டு 2.

திசையன்களின் கொடுக்கப்பட்ட அமைப்பு நேரியல் சார்ந்ததா அல்லது நேரியல் சார்புடையதா என்பதைக் கண்டறியவும்:

1. அ 1 = { -20, -15, - 4 }, அ 2 = { –7, -2, -4 }, அ 3 = { 3, –1, –2 }.

தீர்வு.சமன்பாடுகளின் ஒரே மாதிரியான அமைப்பைக் கவனியுங்கள் அ 1 எக்ஸ் 1 + அ 2 எக்ஸ் 2 + அ 3 எக்ஸ் 3 = Θ

அல்லது விரிவாக்கப்பட்ட வடிவத்தில் (ஆயங்கள் மூலம்)

அமைப்பு ஒரே மாதிரியானது. அது சிதைவடையாதது என்றால், அது உண்டு ஒரே முடிவு. ஒரே மாதிரியான அமைப்பில், பூஜ்ஜியம் (அற்பமான) தீர்வு உள்ளது. இதன் பொருள் இந்த வழக்கில் திசையன்களின் அமைப்பு சுயாதீனமாக உள்ளது. கணினி சீரழிந்தால், அது பூஜ்ஜியமற்ற தீர்வுகளைக் கொண்டுள்ளது, எனவே, அது சார்ந்துள்ளது.

சீரழிவுக்கான அமைப்பை நாங்கள் சரிபார்க்கிறோம்:

= –80 – 28 + 180 – 48 + 80 – 210 = – 106 ≠ 0.

அமைப்பு சிதைவடையாதது மற்றும் இதனால், திசையன்கள் அ 1 , அ 2 , அ 3 நேரியல் சார்பற்றது.

பணிகள்.திசையன்களின் கொடுக்கப்பட்ட அமைப்பு நேரியல் சார்ந்ததா அல்லது நேரியல் சார்புடையதா என்பதைக் கண்டறியவும்:

1. அ 1 = { -4, 2, 8 }, அ 2 = { 14, -7, -28 }.

2. அ 1 = { 2, -1, 3, 5 }, அ 2 = { 6, -3, 3, 15 }.

3. அ 1 = { -7, 5, 19 }, அ 2 = { -5, 7 , -7 }, அ 3 = { -8, 7, 14 }.

4. அ 1 = { 1, 2, -2 }, அ 2 = { 0, -1, 4 }, அ 3 = { 2, -3, 3 }.

5. அ 1 = { 1, 8 , -1 }, அ 2 = { -2, 3, 3 }, அ 3 = { 4, -11, 9 }.

6. அ 1 = { 1, 2 , 3 }, அ 2 = { 2, -1 , 1 }, அ 3 = { 1, 3, 4 }.

7. அ 1 = {0, 1, 1 , 0}, அ 2 = {1, 1 , 3, 1}, அ 3 = {1, 3, 5, 1}, அ 4 = {0, 1, 1, -2}.

8. அ 1 = {-1, 7, 1 , -2}, அ 2 = {2, 3 , 2, 1}, அ 3 = {4, 4, 4, -3}, அ 4 = {1, 6, -11, 1}.

9. திசையன்களின் அமைப்பானது நேர்கோட்டில் சார்ந்து இருக்கும் என்பதை நிரூபியுங்கள்:

a) இரண்டு சம திசையன்கள்;

b) இரண்டு விகிதாசார திசையன்கள்.