В этой статье собраны таблицы синусов, косинусов, тангенсов и котангенсов. Сначала мы приведем таблицу основных значений тригонометрических функций, то есть, таблицу синусов, косинусов, тангенсов и котангенсов углов 0, 30, 45, 60, 90, …, 360 градусов (0, π/6, π/4, π/3, π/2, …, 2π радиан). После этого мы дадим таблицу синусов и косинусов, а также таблицу тангенсов и котангенсов В. М. Брадиса, и покажем, как использовать эти таблицы при нахождении значений тригонометрических функций.
Навигация по странице.
Таблица синусов, косинусов, тангенсов и котангенсов для углов 0, 30, 45, 60, 90, … градусов
Список литературы.
- Алгебра: Учеб. для 9 кл. сред. шк./Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова; Под ред. С. А. Теляковского.- М.: Просвещение, 1990.- 272 с.: ил.- ISBN 5-09-002727-7
- Башмаков М. И. Алгебра и начала анализа: Учеб. для 10-11 кл. сред. шк. — 3-е изд. — М.: Просвещение, 1993. — 351 с.: ил. — ISBN 5-09-004617-4.
- Алгебра и начала анализа: Учеб. для 10-11 кл. общеобразоват. учреждений / А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницын и др.; Под ред. А. Н. Колмогорова.- 14-е изд.- М.: Просвещение, 2004.- 384 с.: ил.- ISBN 5-09-013651-3.
- Гусев В. А., Мордкович А. Г. Математика (пособие для поступающих в техникумы): Учеб. пособие.- М.; Высш. шк., 1984.-351 с., ил.
- Брадис В. М. Четырехзначные математические таблицы: Для общеобразоват. учеб. заведений. — 2-е изд. — М.: Дрофа, 1999.- 96 с.: ил. ISBN 5-7107-2667-2
Изучение тригонометрии мы начнем с прямоугольного треугольника. Определим, что такое синус и косинус, а также тангенс и котангенс острого угла. Это основы тригонометрии.
Напомним, что прямой угол — это угол, равный 90 градусов. Другими словами, половина развернутого угла.
Острый угол — меньший 90 градусов.
Тупой угол — больший 90 градусов. Применительно к такому углу «тупой» — не оскорбление, а математический термин:-)
Нарисуем прямоугольный треугольник. Прямой угол обычно обозначается . Обратим внимание, что сторона, лежащая напротив угла, обозначается той же буквой, только маленькой. Так, сторона, лежащая напротив угла A, обозначается .
Угол обозначается соответствующей греческой буквой .

Гипотенуза прямоугольного треугольника — это сторона, лежащая напротив прямого угла.
Катеты— стороны, лежащие напротив острых углов.
Катет , лежащий напротив угла , называется противолежащим (по отношению к углу ). Другой катет , который лежит на одной из сторон угла , называется прилежащим.
Синус острого угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе:
Косинус острого угла в прямоугольном треугольнике — отношение прилежащего катета к гипотенузе:
Тангенс острого угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему:
Другое (равносильное) определение: тангенсом острого угла называется отношение синуса угла к его косинусу:
Котангенс острого угла в прямоугольном треугольнике — отношение прилежащего катета к противолежащему (или, что то же самое, отношение косинуса к синусу):
Обратите внимание на основные соотношения для синуса, косинуса, тангенса и котангенса, которые приведены ниже. Они пригодятся нам при решении задач.

Давайте докажем некоторые из них.
Хорошо, мы дали определения и записали формулы. А для чего все-таки нужны синус, косинус, тангенс и котангенс?
Мы знаем, что сумма углов любого треугольника равна.
Знаем соотношение между сторонами прямоугольного треугольника. Это теорема Пифагора: .
Получается, что зная два угла в треугольнике, можно найти третий. Зная две стороны в прямоугольном треугольнике, можно найти третью. Значит, для углов — свое соотношение, для сторон — свое. А что делать, если в прямоугольном треугольнике известен один угол (кроме прямого) и одна сторона, а найти надо другие стороны?

С этим и столкнулись люди в прошлом, составляя карты местности и звездного неба. Ведь не всегда можно непосредственно измерить все стороны треугольника.
Синус, косинус и тангенс — их еще называют тригонометрическими функциями угла — дают соотношения между сторонами и углами треугольника. Зная угол, можно найти все его тригонометрические функции по специальным таблицам. А зная синусы, косинусы и тангенсы углов треугольника и одну из его сторон, можно найти остальные.
Мы тоже нарисуем таблицу значений синуса, косинуса, тангенса и котангенса для «хороших» углов от до .
Обратите внимание на два красных прочерка в таблице. При соответствующих значениях углов тангенс и котангенс не существуют.
Разберем несколько задач по тригонометрии из Банка заданий ФИПИ.
1. В треугольнике угол равен , . Найдите .
Задача решается за четыре секунды.
Поскольку , .
2. В треугольнике угол равен , , . Найдите .

Найдем по теореме Пифагора.
Задача решена.
Часто в задачах встречаются треугольники с углами и или с углами и . Основные соотношения для них запоминайте наизусть!

Для треугольника с углами и катет, лежащий напротив угла в , равен половине гипотенузы.
Треугольник с углами и — равнобедренный. В нем гипотенуза в раз больше катета.
Мы рассмотрели задачи на решение прямоугольных треугольников — то есть на нахождение неизвестных сторон или углов. Но это не всё! В вариантах ЕГЭ по математике множество задач, где фигурирует синус, косинус, тангенс или котангенс внешнего угла треугольника . Об этом — в следующей статье.
В статье, мы полностью разберемся, как выглядит таблица тригонометрических значений, синуса, косинуса, тангенса и котангенса. Рассмотрим основное значение тригонометрических функций, от угла в 0,30,45,60,90,…,360 градусов. И посмотрим как пользоваться данными таблицами в вычислении значения тригонометрических функций.Первой рассмотрим таблицу косинуса, синуса, тангенса и котангенса от угла в 0, 30, 45, 60, 90,.. градусов. Определение данных величин дают определить значение функций углов в 0 и 90 градусов:
sin 0 0 =0, cos 0 0 = 1. tg 00 = 0, котангенс от 00 будет неопределеннымsin 90 0 = 1, cos 90 0 =0, ctg90 0 = 0,тангенс от 90 0 будет неопределенным
Если взять прямоугольные треугольники углы которых от 30 до 90 градусов. Получим:
sin 30 0 = 1/2, cos 30 0 = √3/2, tg 30 0 = √3/3, ctg 30 0 = √3sin 45 0 = √2/2, cos 45 0 = √2/2, tg 45 0 = 1, ctg 45 0 = 1sin 60 0 = √3/2, cos 60 0 = 1/2, tg 60 0 =√3 , ctg 60 0 = √3/3
Изобразим все полученные значения в виде тригонометрической таблицы:
Таблица синусов, косинусов, тангенсов и котангенсов!
Если использовать формулу приведения, наша таблица увеличится, добавятся значения для углов до 360 градусов. Выглядеть она будет как:

Так же исходя из свойств периодичности таблицу можно увеличить, если заменим углы на 0 0 +360 0 *z …. 330 0 +360 0 *z, в котором z является целым числом. В данной таблице возможно вычислить значение всех углов, соответствующими точками в единой окружности.

Разберем наглядно как использовать таблицу в решении.Все очень прост. Так как нужное нам значение лежит в точке пересечения нужных нам ячеек. К примеру возьмем cos угла 60 градусов, в таблице это будет выглядеть как:

В итоговой таблице основных значений тригонометрических функций, действуем так же. Но в данной таблице возможно узнать сколько составит тангенс от угла в 1020 градусов, он = -√3 Проверим 1020 0 = 300 0 +360 0 *2. Найдем по таблице.

Таблица Брадиса. Для синуса, косинуса, тангенса и котангенса.
Таблицы Брадиса поделены на несколько частей, состоят из таблиц косинуса и синуса, тангенса и котангенса — которая поделена на две части (tg угла до 90 градусов и ctg малых углов).
Синус и косинус

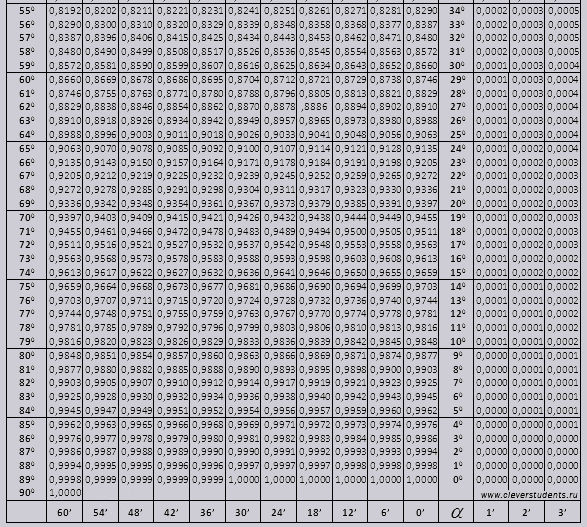
tg угла начиная с 00 заканчивая 760, ctg угла начиная с 140 заканчивая 900.

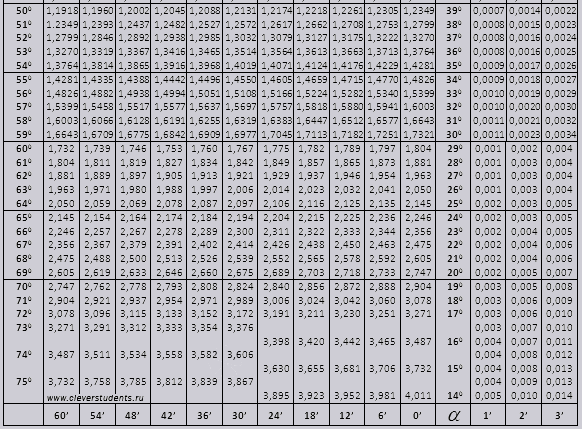
tg до 900 и ctg малых углов.
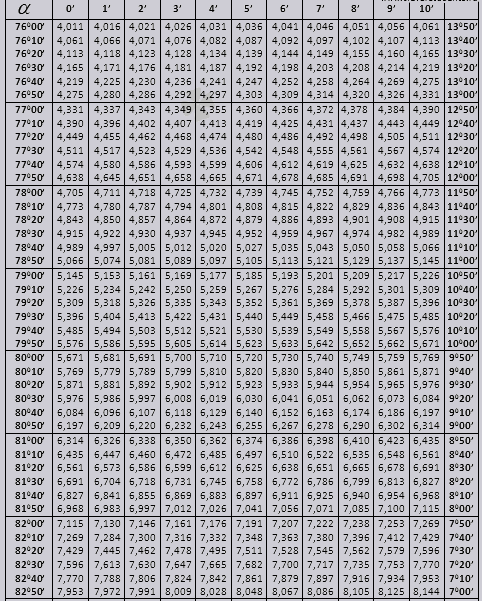
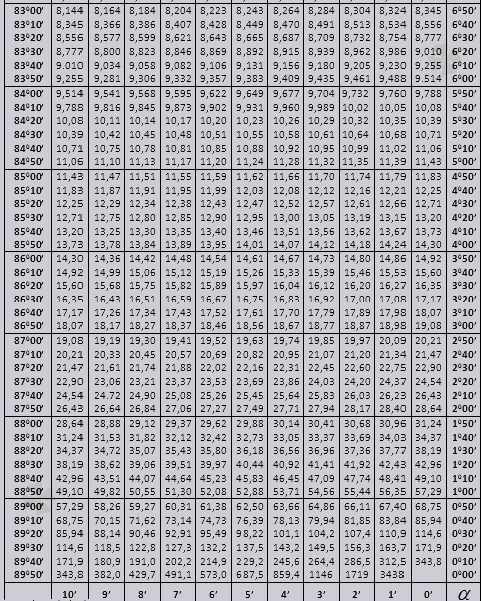
Разберемся как пользоваться таблицами Брадиса в решении задач.
Найдем обозначение sin (обозначение в столбце с левого края) 42 минут (обозначение находится на верхней строчке). Путем пересечения ищем обозначение, оно = 0,3040.Величины минут указаны с промежутком в шесть минут, как быть если нужное нам значение попадет именно в этот промежуток. Возьмем 44 минуты, а в таблице есть только 42. Берем за основу 42 и воспользуемся добавочными столбцами в правой стороне, берем 2 поправку и добавляем к 0,3040 + 0,0006 получаем 0,3046.При sin 47 мин, берем за основу 48 мин и отнимаем от нее 1 поправку, т.е 0,3057 — 0,0003 = 0,3054При вычислении cos работаем аналогично sin только за основу берем нижнюю строку таблицы. К примеру cos 20 0 = 0.9397Значения tg угла до 90 0 и cot малого угла, верны и поправок в них нет. К примеру, найти tg 78 0 37мин = 4,967 а ctg 20 0 13мин = 25,83
а ctg 20 0 13мин = 25,83
Ну вот мы и рассмотрели основные тригонометрические таблицы. Надеемся это информация была для вас крайне полезной. Свои вопросы по таблицам, если они появились, обязательно пишите в комментариях!
Заметка: Стеновые отбойники — отбойная доска для защиты стен. Перейдите по ссылке настенные отбойники бескаркасные (http://www.spi-polymer.ru/otboyniki/) и узнайте подробнее.
Таблица основных тригонометрических функций для углов 0, 30, 45, 60, 90, … градусов
Из тригонометрических определений функций $sin$, $cos$, $tan$ и $cot$ можно узнать их значения для углов $0$ и $90$ градусов:
$sin0°=0$, $cos0°=1$, $tan 0°=0$, $cot 0°$ не определяется;
$sin90°=1$, $cos90°=0$, $cot90°=0$, $tan 90°$ не определяется.
В школьном курсе геометрии при изучении прямоугольных треугольников находят тригонометрические функции углов $0°$, $30°$, $45°$, $60°$ и $90°$.
Найденные значения тригонометрических функций для указанных углов в градусах и радианах соответственно ($0$, $frac{pi}{6}$, $frac{pi}{4}$, $frac{pi}{3}$, $frac{pi}{2}$) для удобства запоминания и использования заносят в таблицу, которую называют тригонометрической таблицей, таблицей основных значений тригонометрических функций и т.п.
При использовании формул приведения, тригонометрическая таблица может быть расширена до угла $360°$ и соответственно $2pi$ радиан:
Применяя свойства периодичности тригонометрических функций, каждый угол, который будет отличаться от уже известного на $360°$, можно рассчитать и записать в таблицу. Например, тригонометрическая функция для угла $0°$ будет иметь такое же значение и для угла $0°+360°$, и для угла $0°+2 cdot 360°$, и для угла $0°+3 cdot 360°$ и т.д.
С помощью тригонометрической таблицы можно определить значения всех углов единичной окружности.
В школьном курсе геометрии предполагается запоминание основных значений тригонометрических функций, собранных в тригонометрической таблице, для удобства решения тригонометрических задач.
Использование таблицы
В таблице достаточно найти необходимую тригонометрическую функцию и значение угла или радиан, для которых эту функцию нужно вычислить. На пересечении строки с функцией и столбца со значением получим искомое значение тригонометрической функции заданного аргумента.
На рисунке можно увидеть, как найти значение $cos60°$, которое равно $frac{1}{2}$.
Аналогично используется расширенная тригонометрическая таблица. Преимуществом ее использования является, как уже упоминалось, вычисление тригонометрической функции практически любого угла. Например, легко можно найти значение $tan 1 380°=tan (1 380°-360°)=tan(1 020°-360°)=tan(660°-360°)=tan300°$:
Таблицы Брадиса основных тригонометрических функций
Возможность расчета тригонометрической функции абсолютно любого значения угла для целого значения градусов и целого значения минут дает использование таблиц Брадиса. Например, найти значение $cos34°7″$. Таблицы разделены на 2 части: таблицу значений $sin$ и $cos$ и таблицу значений $tan$ и $cot$.
Таблицы Брадиса дают возможность получить приближенное значение тригонометрических функций с точностью до 4-х знаков после десятичной запятой.
Использование таблиц Брадиса
Используя таблицы Брадиса для синусов, найдем $sin17°42″$. Для этого в столбце слева таблицы синусов и косинусов находим значение градусов – $17°$, а в верхней строке находим значение минут – $42″$. На их пересечении получаем искомое значение:
$sin17°42″=0,304$.
Для нахождения значения $sin17°44″$ нужно воспользоваться поправкой в правой части таблицы. В данном случае к значению $42″$, которое есть в таблице, нужно добавить поправку для $2″$, которая равна $0,0006$. Получим:
$sin17°44″=0,304+0,0006=0,3046$.
Для нахождения значения $sin17°47″$ также пользуемся поправкой в правой части таблицы, только в этом случае за основу берем значение $sin17°48″$ и отнимаем поправку для $1″$:
$sin17°47″=0,3057-0,0003=0,3054$.
При расчете косинусов выполняем аналогичные действия, но градусы смотрим в правом столбце, а минуты – в нижней колонке таблицы. Например, $cos20°=0,9397$.
Для значений тангенса до $90°$ и котангенса малого угла поправок нет. Например, найдем $tan 78°37″$, который по таблице равен $4,967$.
1. Тригонометрические функции представляют собой элементарные функции, аргументом которых является угол. С помощью тригонометрических функций описываются соотношения между сторонами и острыми углами в прямоугольном треугольнике. Области применения тригонометрических функций чрезвычайно разнообразны. Так, например, любые периодические процессы можно представить в виде суммы тригонометрических функций (ряда Фурье). Данные функции часто появляются при решении дифференциальных и функциональных уравнений.
2. К тригонометрическим функциям относятся следующие 6 функций: синус, косинус, тангенс,котангенс, секанс и косеканс. Для каждой из указанных функций существует обратная тригонометрическая функция.
3. Геометрическое определение тригонометрических функций удобно ввести с помощью единичного круга. На приведенном ниже рисунке изображен круг радиусом r=1. На окружности обозначена точка M(x,y). Угол между радиус-вектором OM и положительным направлением оси Ox равен α.
4. Синусом угла α называется отношение ординаты y точки M(x,y) к радиусу r: sinα=y/r. Поскольку r=1, то синус равен ординате точки M(x,y).
5. Косинусом угла α называется отношение абсциссы x точки M(x,y) к радиусу r: cosα=x/r
6. Тангенсом угла α называется отношение ординаты y точки M(x,y) к ee абсциссе x: tanα=y/x,x≠0
7. Котангенсом угла α называется отношение абсциссы x точки M(x,y) к ее ординате y: cotα=x/y,y≠0
8. Секанс угла α − это отношение радиуса r к абсциссе x точки M(x,y): secα=r/x=1/x,x≠0
9. Косеканс угла α − это отношение радиуса r к ординате y точки M(x,y): cscα=r/y=1/y,y≠0
10. В единичном круге проекции x, y точки M(x,y) и радиус r образуют прямоугольный треугольник, в котором x,y являются катетами, а r − гипотенузой. Поэтому, приведенные выше определения тригонометрических функций в приложении к прямоугольному треугольнику формулируются таким образом: Синусом угла α называется отношение противолежащего катета к гипотенузе. Косинусом угла α называется отношение прилежащего катета к гипотенузе. Тангенсом угла α называется противолежащего катета к прилежащему. Котангенсом угла α называется прилежащего катета к противолежащему. Секанс угла α представляет собой отношение гипотенузы к прилежащему катету. Косеканс угла α представляет собой отношение гипотенузы к противолежащему катету.
11. График функции синус y=sinx, область определения: x∈R, область значений: −1≤sinx≤1
12. График функции косинус y=cosx, область определения: x∈R, область значений: −1≤cosx≤1
13. График функции тангенс y=tanx, область определения: x∈R,x≠(2k+1)π/2, область значений: −∞

14. График функции котангенс y=cotx, область определения: x∈R,x≠kπ, область значений: −∞

15. График функции секанс y=secx, область определения: x∈R,x≠(2k+1)π/2, область значений:secx∈(−∞,−1]∪∪} Популярные материалы

 Способы защиты от влияния энергетического вампира
Способы защиты от влияния энергетического вампира  Акафист священномученику Киприану и мученице Иустине Акафист киприану и иустине православие
Акафист священномученику Киприану и мученице Иустине Акафист киприану и иустине православие  Суп диетический из кабачков Диетический суп из кабачков
Суп диетический из кабачков Диетический суп из кабачков  Значение имени, тайна имени
Значение имени, тайна имени  Вареники с капустой: рецепты
Вареники с капустой: рецепты