La esencia de la teoría de la estadística no paramétrica. El caso de rangos idénticos
El uso de una escala ordinal le permite asignar rangos a objetos según cualquier criterio. Por tanto, los valores de las métricas se convierten en valores de clasificación. Al mismo tiempo, se registran diferencias en el grado de expresión de las propiedades. Hay 2 reglas a seguir durante el proceso de clasificación.
Regla de orden de clasificación. Es necesario decidir quién recibe el primer rango: el objeto con mayor grado de expresión de cualquier cualidad o viceversa. La mayoría de las veces esto es absolutamente indiferente y no afecta el resultado final. Es tradicional asignar el primer rango a los objetos con mayor grado de expresión de calidad (un valor más alto significa un rango más bajo). Por ejemplo, el campeón obtiene el primer lugar y no al revés. Aunque, incluso aquí, si se hubiera adoptado el orden inverso, los resultados no habrían cambiado. Por tanto, cada investigador tiene derecho a determinar él mismo el orden de clasificación. Por ejemplo, E.V. Sidorenko recomienda asignar un rango inferior a un valor menor. En algunos casos es más conveniente, pero más inusual.
Por ejemplo: hay una muestra desordenada cuyos datos deben clasificarse. (2, 7, 6, 8, 11, 15, 9). Después de ordenar la muestra, la clasificamos.
|
Datos métricos |
Opción alternativa: |
Datos métricos | ||
Lo siguiente debe decirse por separado. Existe un grupo de pruebas no paramétricas que rara vez se utilizan (prueba T de Wilcoxon, prueba U de Mann-Whitney, prueba Q de Rosenbaum, etc.), cuando se trabaja con ellas siempre se debe asignar un rango más bajo a un valor más pequeño.
Regla de rangos afines. A los objetos con la misma expresión de propiedades se les asigna el mismo rango. Este rango es el promedio de los rangos que habrían recibido si no hubieran sido iguales. Por ejemplo, necesita clasificar una muestra que contiene varios datos métricos idénticos: (4, 5, 9, 2, 6, 5, 9, 7, 5, 12). Después de ordenar la muestra, se debe calcular la media aritmética de los rangos relacionados.
|
Datos métricos |
Clasificación preliminar |
Clasificación final |
Asignaciones para trabajo independiente.
Clasifique la muestra según la regla “valor más alto - rango más bajo”: (111, 104, 115, 107, 95, 104, 104).
Clasifique la muestra de acuerdo con la regla “valor más bajo – rango más bajo” (20, 25, 8, 7, 20, 14, 27).
Combine las dos muestras anteriores y clasifique según la regla “mayor valor - menor rango”
¿Indicadores de qué características de la Tabla I son nominativas y cuáles son métricas?
Convierta los indicadores de concientización de la Tabla I del Apéndice a una escala de clasificación. Identificar los niveles de expresión de los indicadores traduciéndolos a una escala nominativa.
Tabla I Datos para procesamiento
|
estudiantes |
perfil universitario |
conciencia |
figuras ocultas |
omitido |
aritmética |
inteligencia |
excepción imágenes |
analogías |
serie de números |
inferencias |
suma geométrica |
aprendiendo palabras |
coeficiente intelectual promedio |
extroversión- introversión |
neuroticismo |
marca promedio |
||
Perfil universitario: 0 - perfil humanitario elegido por el estudiante;
1 - elección del estudiante de un perfil de matemáticas o ciencias naturales
Al estudiar la salud pública y la asistencia sanitaria con fines científicos y prácticos, el investigador a menudo tiene que realizar un análisis estadístico de las relaciones entre los factores y las características de desempeño de una población estadística (relación causal) o determinar la dependencia de cambios paralelos en varias características de esta población. en algún tercer valor (en su causa común). Es necesario poder estudiar las características de esta conexión, determinar su tamaño y dirección, así como evaluar su confiabilidad. Para ello se utilizan métodos de correlación.
- Tipos de manifestación de relaciones cuantitativas entre características.
- conexión funcional
- conexión de correlación
- Definiciones de conexión funcional y correlacional
Conexión funcional- este tipo de relación entre dos características cuando cada valor de una de ellas corresponde a un valor estrictamente definido de la otra (el área de un círculo depende del radio del círculo, etc.). La conexión funcional es característica de los procesos físicos y matemáticos.
Correlación- una relación en la que cada valor específico de una característica corresponde a varios valores de otra característica interrelacionada con ella (la relación entre la altura y el peso de una persona; la relación entre la temperatura corporal y la frecuencia del pulso, etc.). La correlación es típica de los procesos médicos y biológicos.
- La importancia práctica de establecer una conexión de correlación. Identificación de causa y efecto entre factores y características de desempeño (al evaluar desarrollo fisico, para determinar la conexión entre las condiciones de trabajo, las condiciones de vida y el estado de salud, al determinar la dependencia de la frecuencia de los casos de enfermedades de la edad, la duración del servicio, la presencia de riesgos laborales, etc.)
Dependencia de cambios paralelos en varias características de algún tercer valor. Por ejemplo, bajo la influencia de altas temperaturas, se producen cambios en el taller. presión arterial, viscosidad de la sangre, frecuencia del pulso, etc.
- Un valor que caracteriza la dirección y la fuerza de la relación entre características.. El coeficiente de correlación, que en un número da una idea de la dirección y fuerza de la conexión entre signos (fenómenos), los límites de sus fluctuaciones de 0 a ± 1.
- Métodos de presentación de correlaciones.
- gráfico (diagrama de dispersión)
- coeficiente de correlación
- Dirección de correlación
- derecho
- contrarrestar
- Fuerza de correlación
- fuerte: ±0,7 a ±1
- promedio: ±0,3 a ±0,699
- débil: 0 a ±0,299
- Métodos para determinar el coeficiente de correlación y fórmulas.
- método de los cuadrados (método de Pearson)
- método de clasificación (método Spearman)
- Requisitos metodológicos para utilizar el coeficiente de correlación.
- medir la relación sólo es posible en poblaciones cualitativamente homogéneas (por ejemplo, medir la relación entre altura y peso en poblaciones homogéneas por género y edad)
- El cálculo se puede realizar utilizando valores absolutos o derivados.
- Los datos no agrupados se utilizan para calcular el coeficiente de correlación. serie de variación(este requisito se aplica solo al calcular el coeficiente de correlación utilizando el método del cuadrado)
- número de observaciones al menos 30
- Recomendaciones para utilizar el método de correlación de rangos (método de Spearman)
- cuando no es necesario establecer con precisión la fuerza de la conexión, pero los datos aproximados son suficientes
- Cuando las características están representadas no sólo por valores cuantitativos, sino también atributivos.
- cuando la serie de características de distribución tenga opciones abiertas (por ejemplo, experiencia laboral de hasta 1 año, etc.)
- Recomendaciones para utilizar el método de los cuadrados (método de Pearson)
- cuando se requiere una determinación precisa de la fuerza de conexión entre características
- cuando los signos sólo tienen expresión cuantitativa
- Metodología y procedimiento para calcular el coeficiente de correlación.
1) Método de los cuadrados
2) método de clasificación
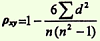
- Esquema para evaluar la relación de correlación utilizando el coeficiente de correlación.
- Cálculo del error del coeficiente de correlación.
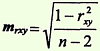
- Estimación de la confiabilidad del coeficiente de correlación obtenido por el método de correlación de rangos y el método de cuadrados
Método 1
La confiabilidad está determinada por la fórmula:
El criterio t se evalúa utilizando una tabla de valores t, teniendo en cuenta el número de grados de libertad (n - 2), donde n es el número de opciones pareadas. El criterio t debe ser igual o mayor que el de la tabla, correspondiendo a una probabilidad p ≥99%.
Método 2
La confiabilidad se evalúa utilizando una tabla especial de coeficientes de correlación estándar. En este caso, un coeficiente de correlación se considera confiable cuando, con un cierto número de grados de libertad (n - 2), es igual o mayor que el tabular, correspondiente al grado de predicción libre de error p ≥95%. .
Ejercicio: Calcule el coeficiente de correlación, determine la dirección y la fuerza de la relación entre la cantidad de calcio en el agua y la dureza del agua, si se conocen los siguientes datos (Tabla 1). Evaluar la confiabilidad de la relación. Obtener una conclusión.
tabla 1
Justificación de la elección del método. Para resolver el problema se optó por el método de los cuadrados (Pearson), porque cada uno de los signos (dureza del agua y cantidad de calcio) tiene una expresión numérica; ninguna opción abierta.
Solución.
La secuencia de cálculos se describe en el texto, los resultados se presentan en la tabla. Habiendo construido series de características comparables pareadas, denotalas por x (dureza del agua en grados) y por y (cantidad de calcio en el agua en mg/l).
| Dureza del agua (en grados) |
Cantidad de calcio en el agua. (en mg/l) |
d x | d y | d x x d y | rex 2 | d y 2 |
| 4 8 11 27 34 37 |
28 56 77 191 241 262 |
-16 -12 -9 +7 +14 +16 |
-114 -86 -66 +48 +98 +120 |
1824 1032 594 336 1372 1920 |
256 144 81 49 196 256 |
12996 7396 4356 2304 9604 14400 |
| Mx =Σx/n | M y =Σ y / n | Σ d x x d y =7078 | Σd x 2 =982 | Σ d y 2 =51056 | ||
| M x =120/6=20 | M y =852/6=142 | |||||
- Determine los valores promedio de M x en la opción de fila “x” y M y en la opción de fila “y” usando las fórmulas:
M x = Σх/n (columna 1) y
M y = Σу/n (columna 2) - Encuentre la desviación (d x y d y) de cada opción del valor del promedio calculado en la serie “x” y en la serie “y”
d x = x - M x (columna 3) y d y = y - M y (columna 4). - Encuentre el producto de las desviaciones d x x d y y resúmalos: Σ d x x d y (columna 5)
- Eleva al cuadrado cada desviación d x y d y y suma sus valores a lo largo de la serie “x” y la serie “y”: Σ d x 2 = 982 (columna 6) y Σ d y 2 = 51056 (columna 7).
- Determine el producto Σ d x 2 x Σ d y 2 y extraiga la raíz cuadrada de este producto
- Los valores resultantes Σ (d x x d y) y √ (Σd x 2 x Σd y 2) sustituya en la fórmula para calcular el coeficiente de correlación:
- Determine la confiabilidad del coeficiente de correlación:
1er método. Encuentre el error del coeficiente de correlación (mr xy) y el criterio t usando las fórmulas:
Criterio t = 14,1, que corresponde a la probabilidad de un pronóstico libre de errores p > 99,9%.
2do método. La confiabilidad del coeficiente de correlación se evalúa utilizando la tabla "Coeficientes de correlación estándar" (ver Apéndice 1). Con el número de grados de libertad (n - 2)=6 - 2=4, nuestro coeficiente de correlación calculado r xу = + 0,99 es mayor que el tabulado (r tabla = + 0,917 en p = 99%).
Conclusión. Cuanto más calcio hay en el agua, más dura es (conexión directo, fuerte y autentico: r xy = + 0,99, p > 99,9%).
utilizar el método de clasificaciónEjercicio: Utilizando el método de clasificación, establezca la dirección y fuerza de la relación entre los años de experiencia laboral y la frecuencia de lesiones si se obtienen los siguientes datos:
Justificación de la elección del método: Para resolver el problema, sólo se puede elegir el método de correlación de rangos, porque La primera fila del atributo "experiencia laboral en años" tiene opciones abiertas (experiencia laboral de hasta 1 año y 7 años o más), lo que no permite el uso de un método más preciso, el método de los cuadrados, para establecer una conexión. entre las características comparadas.
Solución. La secuencia de cálculos se presenta en el texto, los resultados se presentan en la tabla. 2.
Tabla 2
Experiencia laboral en años. Número de lesiones Números ordinales (rangos) diferencia de rango Diferencia al cuadrado de rangos X Y d(xy) re 2 Hasta 1 año 24 1 5 -4 16 1-2 16 2 4 -2 4 3-4 12 3 2,5 +0,5 0,25 5-6 12 4 2,5 +1,5 2,25 7 o más 6 5 1 +4 16 Σd2 = 38,5 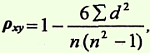
Coeficientes de correlación estándar que se consideran fiables (según L.S. Kaminsky)
Número de grados de libertad - 2 Nivel de probabilidad p (%) 95% 98% 99% 1 0,997 0,999 0,999 2 0,950 0,980 0,990 3 0,878 0,934 0,959 4 0,811 0,882 0,917 5 0,754 0,833 0,874 6 0,707 0,789 0,834 7 0,666 0,750 0,798 8 0,632 0,716 0,765 9 0,602 0,885 0,735 10 0,576 0,858 0,708 11 0,553 0,634 0,684 12 0,532 0,612 0,661 13 0,514 0,592 0,641 14 0,497 0,574 0,623 15 0,482 0,558 0,606 16 0,468 0,542 0,590 17 0,456 0,528 0,575 18 0,444 0,516 0,561 19 0,433 0,503 0,549 20 0,423 0,492 0,537 25 0,381 0,445 0,487 30 0,349 0,409 0,449 - Vlasov V.V. Epidemiología. - M.: GEOTAR-MED, 2004. - 464 p.
- Lisitsyn yu.p. Salud pública y asistencia sanitaria. Libro de texto para universidades. - M.: GEOTAR-MED, 2007. - 512 p.
- Médico V.A., Yuryev V.K. Curso de conferencias sobre salud pública y asistencia sanitaria: Parte 1. Salud pública. - M.: Medicina, 2003. - 368 p.
- Minyaev V.A., Vishnyakov N.I. y otros. Medicina social y organización sanitaria (Manual en 2 tomos). - San Petersburgo, 1998. -528 p.
- Kucherenko V.Z., Agarkov N.M. y otros. Higiene social y organización sanitaria ( Tutorial) - Moscú, 2000. - 432 p.
- S. Glanz. Estadísticas médicas y biológicas. Traducción del inglés - M., Praktika, 1998. - 459 p.
Al analizar los fenómenos socioeconómicos, a menudo es necesario recurrir a diversas estimaciones condicionales utilizando rangos, y la relación entre las características individuales se mide mediante coeficientes de correlación no paramétricos.
que van Es un procedimiento para ordenar objetos de estudio, que se realiza en función de las preferencias.
Rango- este es el número de serie de los valores característicos, ordenados en orden ascendente o descendente de sus valores. Si los valores característicos tienen los mismos cuantificación, entonces el rango de todos estos valores se considera igual a la media aritmética de los números de lugar correspondientes que definen. Estos rangos se llaman conectado.
Entre los métodos no paramétricos para estimar la fuerza de la conexión. valor más alto tienen coeficientes de correlación de rango de Spearman (p1?/) y Kendall (t^). Estos coeficientes se pueden utilizar para determinar la cercanía de la relación entre características cuantitativas y cualitativas.
Coeficiente de correlación de rango(Coeficiente de Spearman) se calcula mediante la fórmula
Dónde (11 - cuadrados de diferencia de rango; PAG - número de observaciones (número de pares de rangos).
El coeficiente de Spearman toma cualquier valor en el intervalo [-1; 1].
Ejemplo. Con base en los datos sobre la compra y venta de moneda por parte de ciudadanos de las entidades constitutivas del Distrito Federal del Volga de la Federación de Rusia a través de organizaciones de crédito en 2010, determinaremos la relación entre estas características utilizando el coeficiente de Spearman (Cuadro 7.14).
Tabla 7.14. Cálculo del coeficiente de Spearman
|
Sujeto |
comprar moneda X, millones de rublos |
Venta de moneda y, millones de rublos |
Rango |
hacer estallar una fila |
Diferencia al cuadrado de rangos $ |
|
|
A |
ry |
|||||
|
1. República de Bashkortostán |
||||||
|
2. República de Mari El |
||||||
|
3. República de Mordovia |
||||||
|
4. República de Tartaristán |
||||||
|
5. República de Udmurtia |
||||||
|
6. Chuvasio República |
||||||
|
7. Región permanente |
||||||
|
8. Región de Kírov |
||||||
|
9. Región de Nizhni Nóvgorod |
||||||
|
10. Región de Oremburgo |
||||||
|
11. Región de Penza |
||||||
|
12. Región de Samara |
||||||
|
13. Región de Sarátov |
||||||
|
14. Región de Uliánovsk |
||||||
Calculemos el coeficiente de correlación de rango de Spearman:
Como resultado del cálculo, determinamos que la conexión entre la compra y venta de moneda por parte de ciudadanos de las entidades constitutivas del Distrito Federal del Volga de la Federación de Rusia a través de organizaciones de crédito en 2010 fue fuerte, casi funcional.
Coeficiente de correlación de rangos de Kendall También se utiliza para medir el grado de cercanía y dirección de conexión entre características cualitativas y cuantitativas que caracterizan objetos homogéneos y se clasifican según el mismo principio. El coeficiente de rango de Kendall se calcula mediante la fórmula
donde 5 es la suma de las diferencias entre el número de secuencias y el número de inversiones según la segunda característica; PAG - número de observaciones.
El cálculo de este coeficiente se realiza en la siguiente secuencia.
- 1. Valores X clasificados en orden ascendente o descendente.
- 2. Valores en están ordenados en orden correspondiente a los valores X.
- 3. Para cada rango en Se determina el número de valores de rango que lo siguen y exceden su valor. Así, sumando números se determina el valor. R como medida de correspondencia entre secuencias de rangos xx y y, que se tiene en cuenta con un signo "+".
- 4. Para cada rango en Se determina el número de valores de rango que lo siguen y son menores que su valor. El valor total se denota por (2 y se fija con un signo “-”.
- 5. Se determina la suma de puntos para todos los miembros de la serie.
La relación entre características se considera estadísticamente significativa si los coeficientes de correlación de rangos de Spearman y Kendall son superiores a 0,5.
Según la tabla. 7.14 obtuvo los resultados presentados en la tabla. 7.15.
Por lo tanto, el coeficiente de correlación de rango de Kendall será
Tabla 7.15.

![]()
lo que también indica una fuerte conexión entre la compra y venta de moneda por parte de ciudadanos de las entidades constitutivas del Distrito Federal del Volga de la Federación de Rusia a través de organizaciones de crédito en 2009.
Coeficiente de correlación de rango múltiple (coeficiente de concordancia) Se utiliza para determinar la cercanía de la relación entre un número arbitrario de características clasificadas. Se calcula mediante la fórmula
![]()
donde 5 es la desviación de la suma de los cuadrados de los rangos del promedio de los cuadrados de los rangos; T- número de factores; PAG - número de observaciones.
Ejemplo. Determinemos el grado de cercanía de la conexión entre indicadores básicos del comercio de tecnología con los países de la CEI en 2010 como el número de acuerdos de exportación, el costo del objeto del acuerdo y el flujo de fondos (Cuadro 7.16).
Tabla 7.16. Cálculo del coeficiente de concordancia.
|
Un país |
Número de acuerdos X |
Costo del objeto del acuerdo. y, Millón de dólares |
Recibo de fondos del año, millones de dólares. |
A |
Suma de filas |
cuadrado de la suma |
||
|
1. Azerbaiyán |
||||||||
|
2. Armenia |
||||||||
|
3. Bielorrusia |
||||||||
|
4. Kazajstán |
||||||||
|
5. Kirguistán |
||||||||
|
6. República de Moldavia |
Al exhibir evaluaciones de expertos o en otros casos de clasificación, surgen situaciones cuando dos o más A las cualidades se les asignan los mismos rangos. En este caso, las reglas de clasificación son:
1. Al valor numérico más pequeño se le asigna el rango 1.
2. Al valor numérico más alto se le asigna una clasificación igual al número de valores clasificados.
3. Si varios valores numéricos iniciales resultan ser iguales, se les asigna un rango igual a promedio aquellos rangos que recibirían estas cantidades si estuvieran en orden una tras otra y no fueran iguales.
Tenga en cuenta que este caso puede incluir tanto el primer como el último valor de la serie original para la clasificación.
4. La suma total de los rangos reales debe coincidir con el calculado, determinado por la fórmula (1).
Por ejemplo, un psicólogo obtuvo los siguientes valores de inteligencia no verbal de 11 sujetos: 113, 107, 123, 122, 117, 117, 105, 108, 114, 102, 104. Es necesario clasificar estos indicadores.
| No. de sujetos | Indicadores de inteligencia | rangos condicionales | Rangos |
| (8) | 8,5 | ||
| (9) | 8,5 | ||
Porque Si 5 y 6 sujetos tienen indicadores de inteligencia iguales, entonces se les deben asignar rangos condicionales, que deben estar en orden uno tras otro, y marcar estos rangos entre paréntesis - (). Pero ya que deben tener los mismos rangos. Luego en la columna de rangos debemos colocar entre paréntesis la media aritmética de los rangos, es decir . A menudo, los rangos condicionales y reales se escriben en la misma columna.
Comprobemos la exactitud de la clasificación utilizando la fórmula (1):
Resumamos los rangos reales: 6+4+11+10+8.5+8.5+3+5+7+1+2=66.
Porque las cantidades coinciden, entonces la clasificación es correcta.
La escala de clasificación utiliza muchos métodos estadísticos. Muy a menudo, los coeficientes de correlación de Spearman y Kendall se aplican a las mediciones obtenidas en esta escala, además, en relación con los datos obtenidos en esta escala, se utilizan una variedad de criterios de diferencia.
Escala de intervalo
En una escala de intervalo, cada uno de los valores posibles de las cantidades medidas se ubica a igual distancia del más cercano. El concepto principal de esta escala es intervalo, que se puede definir como la fracción o fracción de una propiedad medida entre dos posiciones adyacentes en una escala.
Tamaño del intervalo- el valor es fijo y constante en todas las zonas de la escala. Para la medición utilizando una escala de intervalo, se establecen unidades de medida especiales, en psicología esto es paredes. Al trabajar con esta báscula, al bien o elemento que se está midiendo se le asigna un número igual al número de unidades de medida, equivalente a la cantidad del bien presente. Característica importante La escala de intervalo es que no tiene un punto de referencia natural (el cero es arbitrario y no indica la ausencia de la propiedad que se está midiendo).
Así, en psicología se utiliza a menudo el diferencial semántico de Charles Osgood, que es un ejemplo de medición en una escala de intervalos de diversas características psicológicas de un individuo, actitudes sociales, orientaciones valorativas, significado personal subjetivo y diversos aspectos de la autoestima.
3 - 2 - 1 0 +1 +2 +3
Absolutamente no sé nada
en desacuerdo (no estoy seguro) de acuerdo
Sin embargo, como enfatizan S. Stevens y varios otros investigadores, las mediciones psicológicas en una escala de intervalo a menudo resultan, en esencia, ser mediciones realizadas en una escala de orden. La base de esta afirmación es el hecho de que funcionalidad las personas cambian dependiendo de diferentes condiciones. Al medir, por ejemplo, la fuerza con un dinamómetro o la estabilidad de la atención con un cronómetro, los resultados de la medición al principio y al final del experimento no se cuantificarán a intervalos iguales debido a la fatiga del sujeto.
Sólo una medición que utiliza un procedimiento de prueba estrictamente estandarizado, siempre que la distribución de valores en una muestra representativa (ver más abajo) sea lo suficientemente cercana a lo normal (ver más abajo), puede considerarse una medición en una escala de intervalo. Un ejemplo de esto último son las pruebas de inteligencia estandarizadas, donde la unidad de medida convencional del coeficiente intelectual es equivalente tanto para puntuaciones de inteligencia bajas como altas.
También es de fundamental importancia que se pueda aplicar un número bastante grande de métodos estadísticos a los datos experimentales obtenidos en esta escala.
escala de relación
La escala de relaciones se llama también con una escala relaciones iguales. Una característica especial de esta escala es la presencia de un cero firmemente fijo, lo que significa ausencia total cualquier propiedad o signo. La proporción del chacal es la escala más informativa, que permite realizar operaciones matemáticas y el uso de una variedad de métodos estadísticos.
La escala de razón es esencialmente muy cercana a la escala de intervalo, ya que si fija estrictamente el punto de partida, cualquier escala de intervalo se convierte en una escala de razón.
Es en la escala de proporciones donde se realizan mediciones precisas y ultraprecisas en ciencias como la física, la química y la microbiología. Las mediciones de la escala de relaciones también se realizan en ciencias cercanas a la psicología, como la psicofísica, la psicofisiología y la psicogenética.
El coeficiente de cercanía entre características, analizado en la sección anterior, se puede utilizar si las características que se estudian son cuantitativas. En este caso, se utiliza el cálculo de los principales parámetros de distribución (valores medios, varianzas), es decir, método paramétrico.
En la práctica estadística de estudiar fenómenos y procesos socioeconómicos, uno tiene que enfrentar los problemas de medir la relación entre características cualitativas, a las que no son aplicables los métodos de análisis paramétricos en su forma habitual. En este caso, utilice el llamado métodos no paramétricos.
En el análisis de fenómenos socioeconómicos, los coeficientes de correlación de rango (coeficientes de correlación de rango) se utilizan ampliamente cuando los valores no directos de x y y, y ellos filas, aquellos. números de sus lugares ocupados en cada fila de valores en orden ascendente o descendente. Dichos coeficientes no paramétricos incluyen Coeficientes de rango de Spearman Y Kendall.
Si PAG Las opciones de la serie se ordenan de acuerdo con el aumento o disminución de la característica x, luego se dice que los objetos están clasificados según esta característica. El rango de x indica el lugar que ocupa es decir el valor del atributo entre otros PAG valores del atributo x (/ = 1,2,___, PAG).
Por ejemplo, al investigar un mercado, se puede fijar el objetivo de conocer las preferencias de los consumidores a la hora de elegir un producto (al comprar acciones, helado, un coche, etc.) de tal forma que distribuyan el producto de forma ascendente ( (o descendente) de sus preferencias de consumo. Si hay dos conjuntos de datos clasificados, puede establecer el grado dependencia lineal entre ellos.
Ejemplo 6.7. Supongamos que hay 5 productos (Tabla 6.7), que están clasificados en orden de preferencia del 1 al 5 de acuerdo con dos características Ay v.
Clasificaciones originales
Tabla 6.7
Es necesario investigar la cercanía de la relación estadística entre las características.
Solución. Usar el coeficiente de Pearson para determinar la intensidad de la relación entre características será incorrecto, ya que este coeficiente se usa para características que se miden cuantitativamente. Entonces, por ejemplo, al determinar la relación entre altura y peso, medimos la altura en centímetros y el peso en kilogramos, mientras que es posible determinar con precisión en la escala de medición la diferencia en los valores de estas características para cualquier persona (en es decir, la distancia entre ellos en la escala de medición). Tomemos una característica medida en una escala de clasificación: la calificación de un examen. ¿Significa esto que un estudiante que recibió una D tiene la mitad de conocimientos que uno que recibió una B? ¿O dos estudiantes que recibieron calificaciones C tienen exactamente el mismo nivel de conocimiento? La respuesta es no, el profesor organiza su nivel de conocimientos en una secuencia determinada, de acuerdo con los criterios para evaluar el conocimiento en un tema en particular, pero la distancia entre los valores de los signos en dicha escala no está estrictamente fijada.
Para determinar si existe una relación entre las puntuaciones de clasificación, se utiliza Coeficiente de correlación de rangos de Spearman. Su cálculo se basa en las diferencias entre rangos.
Denotemos la diferencia de rango. re = rango A ~ rango EN.
Coeficiente de Spearman
Dónde PAG- número de pares de observaciones clasificadas.
EN Por ejemplo, tenemos cinco pares de rangos, por lo tanto, PAG- 5. Suma Connecticut igual a
Entonces el coeficiente de Spearman

El coeficiente de Spearman varía en el intervalo [-1; 1] y se interpreta de la misma manera que el coeficiente de Pearson. La diferencia es que se calcula a partir de datos clasificados.
Un valor de 0,6 nos permite concluir que existe una relación lineal significativa entre las dos características del producto.
La importancia del coeficiente de Spearman se verifica en función de t Prueba t de Student usando la fórmula
El valor del coeficiente se considera significativo si t calc > > 6fit;a (y - 2) para un nivel de significancia dado a.
El coeficiente de correlación de rangos (siempre que los rangos no se repitan) también se puede calcular utilizando la fórmula propuesta por el estadístico inglés M. Kendall:

Dónde S- diferencia real de rangos; ~n(n- l) - suma máxima de rangos.
Este coeficiente varía en el rango de [-1; 1] y se interpreta de la misma manera que el coeficiente de Pearson, pero da una interpretación más estricta.
evaluación de la conexión que el coeficiente de Spearman, y p = - m. Esta relación se cumple cuando. gran número observaciones (n> 30), y conexiones débiles o moderadamente cercanas.
Al calcular el coeficiente de Kendall, se observa la siguiente secuencia de acciones:
- 1. Los valores de x se clasifican en orden ascendente.
- 2. Valores en están ordenados en orden correspondiente a los valores X.
- 3. Para cada rango y, se determina el número de valores de rango que lo siguen y exceden su valor. El resultado se escribe en la columna “+”.
- 4. Para cada rango en Se determina el número de valores de rango más pequeños que le siguen. El resultado se escribe en la columna “-”.
- 5. El monto se encuentra en la columna “+” y se designa R, en la columna “-” y se designa P. Determinado S = PQ.
La importancia del coeficiente de correlación de rango de Kendall se verifica mediante la fórmula

Dónde sch_ a/2 (p- 2) - cuantil determinado a partir de la tabla de distribución normal para el nivel de significancia seleccionado a y un dado PAG.
Ejemplo 6.8. Calculemos el coeficiente de Kendall con base en los datos del ejemplo 6.7.
Solución. llevemos a cabo cálculos necesarios en mesa 6.8.
De hecho, si el valor obtenido m se multiplica por 1,5, obtenemos 0,6, el valor del coeficiente de Spearman calculado en el ejemplo 6.7.
tabla de cálculo
Consideremos la correlación de características alternativas, es decir, características que toman sólo dos valores posibles. El estudio de su correlación se basa en indicadores construidos en tablas de cuatro celdas, que resumen el número de unidades para valores característicos dados:
Solución. Para medir la cercanía de la relación entre características, el coeficiente contingente se calcula mediante la fórmula

El coeficiente contingente toma valores en el intervalo [-1; 1]. La interpretación es similar al coeficiente de correlación. Tenemos una conexión negativa débil.
Otro método para medir la asociación se basa en calcular el coeficiente de asociación:

„ l 30x5-20x15 l „
Obtenemos: q =-= -0,33
El signo menos delante del coeficiente indica que cuantos más estudiantes fueron vacunados contra la influenza, menor fue la incidencia.
El coeficiente contingente es siempre menor que el coeficiente de asociación y proporciona una evaluación más correcta de la cercanía de la conexión.
Para evaluar la cercanía de la conexión entre características que toman cualquier número de valores variantes (características categóricas, nominales), se utiliza el coeficiente de contingencia mutua de Pearson. La base para estudiar la relación entre características categóricas es una tabla de contingencia: una distribución bidimensional de unidades de población según características. Toda la información sobre la presencia o ausencia de una conexión está contenida en las frecuencias conjuntas de combinaciones de características.
La información para evaluar esta relación se agrupa en forma de tabla (por ejemplo, para tres valores de la primera característica y dos de la segunda), tabla. 6.10.
Tabla 6.10
Ejemplo de tabla de contingencia
|
Firmar |
Total |
|||
|
bgpc |
bjgpc |
Designaciones: eso- frecuencia de combinación mutua de dos características de atributo; PAG = YLmy- número de observaciones.
El coeficiente de contingencia cruzada de Pearson está determinado por la fórmula
donde cp es el índice de conjugación cuadrática media:
El coeficiente de contingencia cruzada toma valores en el intervalo y se interpreta de manera similar al coeficiente de correlación lineal por pares de Pearson.
Ejemplo 6.10. Para estudiar la influencia de las condiciones laborales en las relaciones en el equipo, se realizó una encuesta por muestra a 250 empleados de la empresa, cuyas respuestas se distribuyeron como se presenta en la tabla. 6.11.
Cuadro 6.11
Datos iniciales sobre condiciones laborales y relaciones en el equipo.
Se requiere caracterizar la relación entre los indicadores estudiados utilizando el coeficiente de contingencia mutua de Pearson.
Solución.


El valor obtenido del coeficiente de contingencia indica que la conexión entre las condiciones laborales y las relaciones en el equipo es moderada.
