Éliminer la récursion gauche. Analyse Supprimer la récursion gauche en ligne

Définition. Règle aimable $ est appelé règle d'annulation.

Le dispositif de commande fonctionne selon règles de transition, qui représentent l'algorithme, réalisable cette machine de Turing. Chaque règle de transition demande à la machine, en fonction de l'état actuel et du symbole observé dans la cellule actuelle, d'écrire dans cette cellule nouveau symbole, passez à un nouvel état et déplacez une cellule vers la gauche ou la droite. Certains états de la machine de Turing peuvent être étiquetés comme suit : Terminal, et accéder à l'un d'entre eux signifie la fin du travail, l'arrêt de l'algorithme.

Une machine de Turing s'appelle déterministe, si chaque combinaison d'état et de symbole de ruban dans le tableau correspond à au plus une règle. S'il existe une paire "symbole du ruban - état" pour laquelle il y a 2 instructions ou plus, une telle machine de Turing est appelée non déterministe.

en commençant et en continuant avec les k bornes mentionnées.

Une grammaire est appelée grammaire LL(k) si elle est une grammaire LL(k) pour certains k.

Exemple 4.7. Considérez la grammaire G = ((S, A, B), (0, 1, a, b), P, S), où P est constitué de règles

S -> A | B, A -> aAb | 0, B -> aBbb | 1.

Ici . G n'est pas une grammaire LL (k) pour tout k. Intuitivement, si nous commençons par lire une chaîne de caractères suffisamment longue a , nous ne savons pas laquelle des règles S -> A et S -> B a été appliquée en premier jusqu'à ce que nous rencontrions 0 ou 1 .

Adressage définition précise LL (k)-grammaires, put et y = a k 1b 2k . Puis conclusions

correspondent aux conclusions (1) et (2) de la définition. Les k premiers caractères des chaînes x et y sont identiques. Cependant, la conclusion est fausse. Puisque k est choisi ici arbitrairement, G n’est pas une grammaire LL.

Conséquences de la définition de la grammaire LL(k)

Théorème 4.6. Grammaire KS est une grammaire LL(k) si et seulement si pour deux règles différentes et du carrefour P vide avec tout ça , Quoi .

Preuve. Nécessité. Supposons cela et satisfaisons aux conditions du théorème, et contient x . Alors, par la définition de FIRST, pour certains y et z il y a des conclusions

(Notez qu'ici nous avons profité du fait que N ne contient pas de non-terminaux inutiles, comme cela est supposé pour toutes les grammaires considérées.) Si |x|< k ; то y = z = e . Так как , то G не LL (k)- грамматика .

Adéquation. Supposons que G n’est pas une grammaire LL(k).

Il y a alors deux conclusions

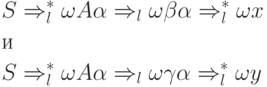
que les chaînes x et y coïncident dans les k premières positions, mais . C'est pourquoi - règles différentes de P et chacun des ensembles Et contient la chaîne PREMIER k (x) coïncidant avec la chaîne PREMIER k (y).

Exemple 4.8. Une grammaire G composée de deux règles S -> aS | a ne sera pas une grammaire LL(1), puisque

PREMIER 1 (aS) = PREMIER 1 (a) = a.

Intuitivement, cela peut s'expliquer ainsi : en voyant uniquement ce premier caractère lors de l'analyse d'une chaîne commençant par le symbole a, on ne sait pas laquelle des règles S -> aS ou S -> a doit être appliquée à S. D’un autre côté, G est une grammaire LL(2). En effet, dans la notation du théorème qui vient d'être présenté, si , alors A = S et . Puisque seules les deux règles indiquées sont données pour S, alors . Puisque FIRST2(aS) = aa et FIRST2(a) = a, alors d'après le dernier théorème G sera une LL (2)-grammaire.

Supprimer la récursion gauche

La principale difficulté lors de l’utilisation de l’analyse prédictive est de trouver une grammaire pour le langage d’entrée qui peut être utilisée pour créer un tableau d’analyse avec des entrées définies de manière unique. Parfois, avec quelques transformations simples, une grammaire non-LL(1) peut être réduite à une grammaire LL(1) équivalente. Parmi ces transformations, les plus efficaces sont la factorisation à gauche et la suppression de la récursion à gauche. Deux points doivent être soulignés ici. Premièrement, toutes les grammaires ne deviennent pas LL(1) après ces transformations, et deuxièmement, après de telles transformations, la grammaire résultante peut devenir moins compréhensible.

La récursivité directe vers la gauche, c'est-à-dire la récursivité du formulaire, peut être supprimée de la manière suivante. Nous regroupons d’abord les règles A :

où aucune des lignes ne commence par A . Ensuite, nous remplaçons cet ensemble de règles par

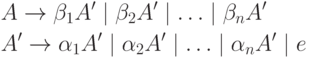
où A" est le nouveau non-terminal. Les mêmes chaînes peuvent être déduites du non-terminal A comme auparavant, mais maintenant il n'y a plus de récursion gauche. Cette procédure supprime toutes les récursions gauches immédiates, mais ne supprime pas la récursion gauche impliquant deux étapes ou plus. Étant donné ci-dessous algorithme 4.8 vous permet de supprimer toutes les récursions gauches de la grammaire.

Algorithme 4.8. Suppression de la récursion gauche.

Entrée. KS-grammaire G sans e-règles (de la forme A -> e ).

Sortie. KS-grammar G" sans récursion gauche, équivalent à G.

Méthode. Suivez les étapes 1 et 2.

(1) Disposez les non-terminaux de la grammaire G dans n'importe quel ordre.

(2) Effectuez la procédure suivante :

Après la (i-1)ème itération de la boucle externe à l'étape 2 pour toute règle de la forme , où k< i , выполняется s >k. En conséquence, à l'itération suivante (par i), la boucle interne (par j) augmente successivement la limite inférieure de m dans n'importe quelle règle , jusqu'à ce qu'il y ait m >= i . Ensuite, après avoir supprimé la récursion immédiate à gauche pour les règles A i, m devient supérieur à i.

Une grammaire contenant une récursion gauche n'est pas une grammaire LL(1). Regardons les règles

UN→ Aa(récursion à gauche dans A)

UN→ un

Ici un symbole prédécesseur pour les deux variantes non terminales UN. De même, une grammaire contenant une boucle récursive gauche ne peut pas être une grammaire LL(1), par exemple

UN→ AVANT JC.

B→ CD

C→ A.E.

Une grammaire contenant une boucle récursive gauche peut être convertie en une grammaire contenant uniquement une récursion directe gauche, puis, en introduisant des non-terminaux supplémentaires, la récursion gauche peut être entièrement éliminée (en effet, elle est remplacée par une récursion droite, ce qui ne pose pas de problème par rapport à LL(1) -propriétés).

A titre d'exemple, considérons une grammaire avec des règles génératives

S→ Aa

UN→ Sib

B→ Cc

C→ Jj

C→ e

D→ Az

qui a une boucle récursive gauche impliquant A B C D. Pour remplacer cette boucle par une récursion directe à gauche, nous ordonnons les non-terminaux comme suit : S, A, B, C, D.

Considérons toutes les règles génératrices de la forme

XI→ Xj γ,

Où XI Et Xj sont des non-terminaux, et γ – une chaîne de caractères terminaux et non terminaux. Concernant les règles pour lesquelles j ≥ je, aucune mesure n'est prise. Cependant, cette inégalité ne peut pas s’appliquer à toutes les règles s’il existe un cycle récursif à gauche. Avec l’ordre que nous avons choisi, nous avons affaire à une seule règle :

D→ Az

parce que UN précédé D dans cet ordre. Commençons maintenant à remplacer UN, en utilisant toutes les règles qui ont UN sur le côté gauche. En conséquence nous obtenons

D→ Bbz

Parce que le B précédé D lors de la commande, le processus est répété, donnant la règle :

D→ CCbz

Puis il se répète et donne deux règles :

D→ ECBZ

D→ Ddcbz

La grammaire convertie ressemble maintenant à ceci :

S→ Aa

UN→ Sib

B→ Cc

C→ Jj

C→ e

D→ Ddcbz

D→ ECBZ

Toutes ces règles génératrices ont la forme requise, et la boucle récursive gauche est remplacée par une récursion directe gauche. Pour éliminer la récursion directe à gauche, nous introduisons un nouveau symbole non terminal Z et changer les règles

D→ ECBZ

D→ Ddcbz

D→ ECBZ

D→ ecbzZ

Z→ DCBZ

Z→ dcbzZ

Notez qu'avant et après la transformation D génère une expression régulière

(ecbz) (dcbz)*

En généralisant, on peut montrer que si un non-terminal UN apparaît sur les côtés gauches r+ s générer des règles, r dont la récursion directe à gauche est utilisée, et s– non, c'est-à-dire

UN→ Aα 1, UN→ Aα 2,..., UN→ Aα r

UN→ β 1, UN→ β 2,..., UN→ β s

alors ces règles peuvent être remplacées par les suivantes :

Une preuve informelle est qu'avant et après la transformation UN génère une expression régulière ( β 1 | β 2 |... | β s) ( α 1 | α 2 |... | α r) *

Il convient de noter qu'en éliminant la récursion gauche (ou boucle récursive gauche), on n'obtient toujours pas une grammaire LL(1), car Pour certains non-terminaux, il existe des côtés droits alternatifs sur le côté gauche des règles des grammaires résultantes, commençant par les mêmes symboles. Par conséquent, après avoir éliminé la récursion gauche, nous devrions continuer à convertir la grammaire sous la forme LL(1).

17.Conversion des grammaires sous la forme LL(1). Factorisation.

Factorisation

Dans de nombreuses situations, les grammaires qui n'ont pas la fonctionnalité LL(1) peuvent être converties en grammaires LL(1) à l'aide du processus de factorisation. Regardons un exemple d'une telle situation.

P.→ commencer D; AVEC fin

D→ d, D

D→ d

AVEC→ s; AVEC

AVEC→ s

Dans le processus de factorisation, nous remplaçons plusieurs règles pour un non-terminal du côté gauche, dont le côté droit commence par le même symbole (chaîne de caractères) par une règle, où du côté droit le début commun est suivi d'un autre introduit non terminal. La grammaire est également complétée par des règles pour un non-terminal supplémentaire, selon lesquelles divers « résidus » du membre droit d'origine de la règle en sont dérivés. Pour la grammaire ci-dessus, cela donnera la grammaire LL(1) suivante :

P.→ commencer D; AVEC fin

D→ dX X)

X→ , D(selon la 1ère règle pour D grammaire originale pour d devrait D)

X→ ε (selon la 2ème règle pour D grammaire originale pour d rien (ligne vide))

AVEC→ s Oui(introduire un non-terminal supplémentaire Oui)

Oui→ ; AVEC(selon la 1ère règle pour C grammaire originale pour s suit ; C)

Oui→ ε (selon la 2ème règle pour C grammaire originale pour s rien (ligne vide))

De même, les règles génératives

S→ asb

S→ asc

S→ ε

peut être converti par factorisation en règles

S→ aSX

S→ ε

X→ b

X→ c

et la grammaire résultante est LL(1). Le processus de factorisation ne peut cependant pas être automatisé en l’étendant au cas général. L'exemple suivant montre ce qui peut arriver. Regardons les règles

1. P.→ Qx

2. P.→ Ry

3. Q→ m²

4. Q→ q

5. R.→ sRN

6. R.→ r

Les deux jeux de caractères guides pour deux options P. contenir s, et en essayant de "endurer s entre parenthèses", nous remplaçons Q Et R.à droite des règles 1 et 2 :

P.→ sQmx

P.→ sRny

P.→ qx

P.→ ry

Ces règles peuvent être remplacées par les suivantes :

P.→ qx

P.→ ry

P.→ SP 1

P. 1 → Qmx

P. 1 → Rny

Règles pour P1 semblable aux règles originales pour P. et avoir des ensembles de personnages guides qui se croisent. Nous pouvons transformer ces règles de la même manière que les règles de P.:

P. 1 → sQmmx

P. 1 → qmx

P. 1 → srnny

P. 1 → rny

En factorisant, on obtient

La procédure d'analyse récursive descendante peut provoquer un problème de boucle infinie.

Dans une grammaire pour opérations arithmétiques, l’application de la deuxième règle entraînera une boucle dans la procédure d’analyse. De telles grammaires sont dites récursives à gauche. Une grammaire est dite récursive à gauche si elle contient un A non terminal pour lequel il existe une conclusion A=>+Aa. Dans les cas simples, la récursion à gauche est provoquée par des règles de la forme

Dans ce cas, un nouveau non-terminal est introduit et les règles originales sont remplacées par les suivantes.

(s'il existe un non-terminal A pour lequel il existe une conclusion A→+Aa en 1 ou plusieurs étapes). La récursion à gauche peut être évitée en transformant la grammaire.

Par exemple, les produits A→Aa

Peut être remplacé par des équivalents :

Pour un tel cas, il existe un algorithme qui élimine la récursion gauche :

1) nous définissons un certain ordre sur l'ensemble des non-terminaux (A 1, A 2, ..., A n)

2) prendre chaque non-terminal s'il existe une production pour lui qui prend en compte le non-terminal de gauche, et transformer la grammaire :

pour i:=1 à n faire

pour j:=1 à i-1 faire

si Ai → Ajγ alors Ai→δ1γ

│ δkγ, où

Aj → δ1│ δ2│ …│ δk

3) exclure tous les cas de récursion immédiate à gauche (règle 1)

Que. L'algorithme permet d'éviter les boucles.

Exclure la récursion gauche de la grammaire des expressions arithmétiques et de la forme générale de la règle d'élimination de la récursion gauche :

Vue générale de la règle d'élimination de la récursivité gauche

Factorisation à gauche.

Les grammaires LL(1) sont nécessaires afin de sélectionner les produits souhaités pour une analyse descendante, afin qu'aucune boucle ne se produise.

Parfois, il est possible de convertir la grammaire sous la forme LL(1) en utilisant la méthode de factorisation à gauche.

Par exemple : S→ si B alors S

│si B alors S sinon S

Ces productions violent la condition des grammaires LL(1). Cette grammaire peut être convertie sous la forme LL(1).

S → si B alors S Queue

DANS vue générale cette transformation peut être définie ainsi :

nous introduisons un nouveau non-terminal B, pour lequel

| β N Pour B nous pouvons appliquer la factorisation à gauche. Cette procédure est répétée tant que le choix du produit reste incertain (c'est-à-dire tant que quelque chose peut y être modifié).

Construction du PREMIER ensemble

Le Premier ensemble pour un non-terminal définit l'ensemble de terminaux à partir duquel ce non-terminal peut partir.

1. Si x est un terminal, alors first(x)=(x). Puisque le premier caractère d’une séquence provenant d’un terminal ne peut être que le terminal lui-même.

2. Si la grammaire contient la règle Xà e, alors l'ensemble first(x) inclut e. Cela signifie que X peut commencer par une séquence vide, c’est-à-dire être totalement absente.

3. Pour tous les produits de la forme XàY1 Y2 … Yk nous effectuons ce qui suit. Nous ajoutons l'ensemble first(Yi) à l'ensemble first(X) jusqu'à ce que first(Yi-1) contienne e et first(Yi) ne contienne pas e. Dans ce cas, i passe de 0 à k. Ceci est nécessaire car si Yi-1 peut manquer, alors il est nécessaire de savoir où commencera toute la séquence dans ce cas.

Propriété LL(k) impose de grandes restrictions à la grammaire. Parfois, il est possible de transformer une grammaire de telle sorte que la grammaire résultante ait propriété LL(1) . Une telle transformation ne réussit pas toujours, mais s'il est possible d'obtenir une grammaire LL(1), alors pour construire un analyseur, vous pouvez utiliser la méthode de descente récursive sans revenir en arrière.

Supposons que nous devions créer un analyseur pour un langage généré par la grammaire suivante :

E → E + T | E – T | T

T → T * F | V/F | F

F → num | (E)

Plusieurs terminaux PREMIER(T) appartiennent également à l'ensemble PREMIER(E+T), il est donc impossible de déterminer sans ambiguïté la séquence d'appels de procédure qui doit être effectuée lors de l'analyse de la chaîne d'entrée. Le problème est que le non-terminal E se produit dans la première position du côté droit de la règle, dont le côté gauche est également E. Dans une telle situation, le non-terminal E est appelé récursif directement gauche.

Non terminal UN Grammaires KS g appelé gauche récursive , s'il y a une conclusion dans la grammaire UN =>* Oh.

Une grammaire qui a au moins une règle récursive gauche ne peut pas être LL(1)-grammaire.

D’autre part, on sait que tout langage CS est défini par au moins une grammaire récursive non gauche.

1. Algorithme pour éliminer la récursivité gauche

Laisser G = (N, T, P, S)– Grammaire et règle KS A → Aw 1 | Oh 2 | ... | Oh n | v 1 | v 2 | ... | v m représente toutes les règles de P. contenant UN sur le côté gauche, et aucune des chaînes v je ne commence pas par un non-terminal UN.

Ajoutons à l'ensemble N un autre non-terminal UN" et remplacer les règles contenant UN sur le côté gauche, à ce qui suit :

UNE → v 1 | v 2 | ... | v m | v 1 UN' | v 2 Un' | ... | v m UN"

A' → w 1 | w 2 | ... | w n | w 1 Un' | w 2 Un' | ...| w n UN"

On peut prouver que la grammaire résultante est équivalente à celle d’origine.

En appliquant cette transformation à la grammaire ci-dessus décrivant des expressions arithmétiques, nous obtenons la grammaire suivante :

E → T | T.E."

E" → + T | + T.E."

T → F | F.T."

T"→ * F | * F.T."

F → (E) | num

Il est facile de montrer que la grammaire résultante a la propriété LL(1).

Un autre problème similaire se produit lorsque deux règles pour le même non-terminal commencent par les mêmes caractères.

Par exemple,

S → si E alors S sinon S

S → si E alors S

Dans ce cas, nous ajouterons un autre non-terminal qui correspondra aux différentes terminaisons de ces règles. Nous obtenons les règles suivantes :

S → si E alors S S’

S" →

S"→ autre S

Pour la grammaire résultante, la méthode de descente récursive peut être implémentée.

1. 9.1.4. Descente récursive avec retours.

Afin de pouvoir appliquer la méthode de descente récursive, il faut 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 transformer la grammaire en une forme dans laquelle des ensembles D'ABORD ne se croisent pas, ce qui est un processus complexe, donc en pratique une technique appelée descente récursive avec retours .

Pour ce faire, l'analyseur lexical est représenté comme un objet qui, en plus des méthodes traditionnelles analyse, suivant etc., il existe également un constructeur de copie. Ensuite, dans toutes les situations où une ambiguïté peut survenir, avant de commencer l'analyse, vous devez vous souvenir de l'état actuel de l'analyseur lexical (c'est-à-dire faire une copie de l'analyseur lexical) et continuer l'analyse du texte, en considérant qu'il s'agit du premier des les constructions possibles dans cette situation. Si cette option d'analyse échoue, vous devez alors restaurer l'état de l'analyseur lexical et essayer d'analyser à nouveau le même fragment en utilisant option suivante grammaire, etc. Si toutes les options d'analyse échouent, une erreur est signalée.

Cette méthode d'analyse est potentiellement plus lente que la descente récursive sans retour en arrière, mais dans ce cas parvient à garder la grammaire dans son forme originale et économisez les efforts du programmeur.