Formule korijena. Svojstva korijena. Kako umnožiti korijenje? Primjeri. Korijen. Akcije s kvadratnim korijenom. Modul. Usporedba kvadratnih korijena
Potenciranje uključuje množenje određenog broja samim sobom određeni broj puta. Na primjer, dizanje broja 2 na petu potenciju izgledalo bi ovako:
Broj koji treba pomnožiti sam sa sobom naziva se baza potencije, a broj množenja njezin eksponent. Podizanje na potenciju odgovara dvjema suprotnim radnjama: pronalaženju eksponenta i pronalaženju baze.
Vađenje korijena
Pronalaženje baze potencije naziva se vađenje korijena. To znači da trebate pronaći broj koji treba podići na potenciju n da biste dobili zadani.
Na primjer, potrebno je izvući 4. korijen broja 16, tj. da biste odredili, trebate pomnožiti sam sa sobom 4 puta da biste na kraju dobili 16. Ovaj broj je 2.
Ova aritmetička operacija se piše posebnim znakom - radikalom: √, iznad kojeg je s lijeve strane označen eksponent.
Aritmetički korijen
Ako je eksponent paran broj, tada korijen mogu biti dva broja s istom apsolutnom vrijednošću, ali c je pozitivan i negativan. Dakle, u navedenom primjeru to bi mogli biti brojevi 2 i -2.
Izraz mora biti nedvosmislen, tj. imati jedan rezultat. U tu svrhu uveden je pojam aritmetičkog korijena koji može predstavljati samo pozitivan broj. Aritmetički korijen ne može biti manji od nule.
Dakle, u primjeru koji je gore razmotren, samo će broj 2 biti aritmetički korijen, a druga opcija odgovora - -2 - isključena je po definiciji.
Korijen
Za neke stupnjeve, koji se koriste češće od drugih, postoje posebni nazivi koji su izvorno povezani s geometrijom. Govorimo o dizanju na drugu i treću potenciju.
Na drugu potenciju duljina stranice kvadrata kada trebate izračunati njegovu površinu. Ako trebate pronaći obujam kocke, duljina njezinog ruba podiže se na treću potenciju. Stoga se zove kvadrat broja, a trećina se zove kocka.
Prema tome, korijen drugog stupnja zove se kvadratni, a korijen trećeg stupnja kubni. Kvadratni korijen je jedini korijen koji se ne piše s eksponentom iznad radikala:
Dakle, aritmetički kvadratni korijen zadanog broja je pozitivan broj koji se mora podići na drugu potenciju da bi se dobio zadani broj.
Održavanje vaše privatnosti važno nam je. Iz tog razloga razvili smo Politiku privatnosti koja opisuje kako koristimo i pohranjujemo vaše podatke. Pregledajte naše prakse privatnosti i javite nam ako imate bilo kakvih pitanja.
Prikupljanje i korištenje osobnih podataka
Osobni podaci odnose se na podatke koji se mogu koristiti za identifikaciju ili kontaktiranje određene osobe.
Od vas se može tražiti da date svoje osobne podatke u bilo kojem trenutku kada nas kontaktirate.
U nastavku su navedeni neki primjeri vrsta osobnih podataka koje možemo prikupljati i kako možemo koristiti takve podatke.
Koje osobne podatke prikupljamo:
- Kada podnesete prijavu na stranici, možemo prikupiti razne podatke, uključujući vaše ime, broj telefona, adresu e-pošte itd.
Kako koristimo vaše osobne podatke:
- Osobni podaci koje prikupljamo omogućuju nam da Vas kontaktiramo i informiramo jedinstvene ponude, promocije i druga događanja te nadolazeća događanja.
- S vremena na vrijeme možemo koristiti vaše osobne podatke za slanje važnih obavijesti i komunikacija.
- Osobne podatke također možemo koristiti u interne svrhe, kao što je provođenje revizija, analiza podataka i raznih istraživanja kako bismo poboljšali usluge koje pružamo i dali vam preporuke u vezi s našim uslugama.
- Ako sudjelujete u izvlačenju nagrada, natjecanju ili sličnoj promociji, možemo koristiti podatke koje nam dostavite za upravljanje takvim programima.
Otkrivanje informacija trećim stranama
Podatke koje smo dobili od vas ne otkrivamo trećim stranama.
Iznimke:
- Po potrebi - sukladno zakonu, sudskom postupku, pravnim postupcima i/ili na temelju javnih zahtjeva ili zahtjeva od vladine agencije na području Ruske Federacije - otkrijte svoje osobne podatke. Također možemo otkriti podatke o vama ako utvrdimo da je takvo otkrivanje potrebno ili prikladno za sigurnosne svrhe, provedbu zakona ili druge svrhe javnog zdravlja. važnim slučajevima.
- U slučaju reorganizacije, spajanja ili prodaje, možemo prenijeti osobne podatke koje prikupimo primjenjivoj trećoj strani nasljedniku.
Zaštita osobnih podataka
Poduzimamo mjere opreza - uključujući administrativne, tehničke i fizičke - kako bismo zaštitili vaše osobne podatke od gubitka, krađe i zlouporabe, kao i neovlaštenog pristupa, otkrivanja, izmjene i uništenja.
Poštivanje vaše privatnosti na razini tvrtke
Kako bismo osigurali sigurnost vaših osobnih podataka, našim zaposlenicima priopćavamo standarde privatnosti i sigurnosti i strogo provodimo prakse privatnosti.
Racionalni brojeviNenegativan kvadratni korijen pozitivnog broja naziva se aritmetički kvadratni korijen i označava se znakom radikala.
Kompleksni brojevi
Nad poljem kompleksnih brojeva uvijek postoje dva rješenja, koja se razlikuju samo predznakom (osim korijen od nule). Korijen kompleksnog broja često se označava kao , ali ovu oznaku morate koristiti pažljivo. Uobičajena greška:
Za izvlačenje kvadratnog korijena kompleksnog broja prikladno je koristiti eksponencijalni oblik zapisivanja kompleksnog broja: if
,gdje se korijen modula shvaća u smislu aritmetičke vrijednosti, a k može imati vrijednosti k=0 i k=1, tako da odgovor završava s dva različita rezultata.
Generalizacije
Kvadratni korijeni uvode se kao rješenja jednadžbi oblika za druge objekte: matrice, funkcije, operatore itd. Kao operacija mogu se koristiti sasvim proizvoljne multiplikativne operacije, npr. superpozicija.
Kvadratni korijen u informatici
U mnogim programskim jezicima funkcionalnoj razini(kao iu označnim jezicima kao što je LaTeX) funkcija kvadratnog korijena označava se kao sqrt(s engleskog korijen"Korijen").
Algoritmi za iznalaženje kvadratnog korijena
Traženje ili izračunavanje kvadratnog korijena dati broj nazvao izvlačenje(korijen.
Proširenje Taylorovog niza
u .Aritmetički kvadratni korijen
Za kvadrate brojeva vrijede sljedeće jednakosti:
To jest, možete saznati cijeli dio kvadratnog korijena broja tako da od njega oduzmete sve neparne brojeve redom dok ostatak ne bude manji od sljedećeg oduzetog broja ili jednak nuli, i brojeći broj izvršenih radnji. Na primjer, ovako:
3 koraka su dovršena, kvadratni korijen iz 9 je 3.
Nedostatak ove metode je da ako korijen koji se izdvaja nije cijeli broj, tada možete saznati samo cijeli njegov dio, ali ne i preciznije. U isto vrijeme, ova metoda je prilično dostupna djeci koja rješavaju jednostavne matematičke probleme koji zahtijevaju izvlačenje kvadratnog korijena.
Gruba procjena
Mnogi algoritmi za izračun kvadratni korijeni od pozitivnog realnog broja S zahtijevaju neku početnu vrijednost. Ako je početna vrijednost predaleko od stvarne vrijednosti korijena, izračuni postaju sporiji. Stoga je korisno imati grubu procjenu, koja može biti vrlo neprecizna, ali je lako izračunati. Ako S≥ 1, neka D bit će broj znamenki S lijevo od decimalne točke. Ako S < 1, пусть D bit će broj uzastopnih nula desno od decimalne točke, uzeto s znakom minus. Tada gruba procjena izgleda ovako:
Ako D neparan, D = 2n+ 1, zatim koristite ![]() Ako Dčak, D = 2n+ 2, zatim upotrijebite
Ako Dčak, D = 2n+ 2, zatim upotrijebite ![]()
Dva i šest koriste se jer ![]() I
I
Kada radite u binarnom sustavu (kao unutar računala), treba koristiti drugačije vrednovanje (ovdje D je broj binarnih znamenki).
Geometrijski kvadratni korijen
Za ručno izdvajanje korijena koristi se zapis sličan dugom dijeljenju. Zapisan je broj čiji korijen tražimo. Desno od njega postupno ćemo dobiti brojeve željenog korijena. Uzmimo korijen broja s konačnim brojem decimalnih mjesta. Za početak, mentalno ili s oznakama, podijelimo broj N u skupine od dvije znamenke lijevo i desno od decimalne točke. Ako je potrebno, grupe se dopunjuju nulama - cjelobrojni dio je dopunjen lijevo, razlomački dio desno. Dakle, 31234.567 se može predstaviti kao 03 12 34. 56 70. Za razliku od dijeljenja, rušenje se provodi u takvim skupinama od 2 znamenke.
Vizualni opis algoritma:
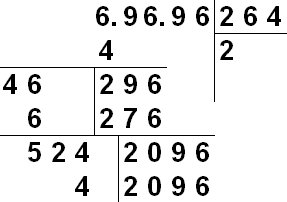
činjenica 1.
\(\bullet\) Uzmimo neki nenegativan broj \(a\) (tj. \(a\geqslant 0\) ). Zatim (aritmetika) korijen od broja \(a\) naziva se takav nenegativan broj \(b\) , kada se na kvadrat dobije broj \(a\) : \[\sqrt a=b\quad \text(isto kao )\quad a=b^2\] Iz definicije proizlazi da \(a\geqslant 0, b\geqslant 0\). Ova ograničenja su važan uvjet postojanje kvadratnog korijena i treba ih zapamtiti!
Podsjetimo se da svaki broj kada se na kvadrat daje nenegativan rezultat. Odnosno, \(100^2=10000\geqslant 0\) i \((-100)^2=10000\geqslant 0\) .
\(\bullet\) Čemu je jednako \(\sqrt(25)\)? Znamo da \(5^2=25\) i \((-5)^2=25\) . Budući da po definiciji moramo pronaći nenegativan broj, tada \(-5\) nije prikladno, dakle \(\sqrt(25)=5\) (jer \(25=5^2\) ).
Pronalaženje vrijednosti \(\sqrt a\) naziva se vađenjem kvadratnog korijena iz broja \(a\), a broj \(a\) naziva se radikalni izraz.
\(\bullet\) Na temelju definicije, izraza \(\sqrt(-25)\), \(\sqrt(-4)\), itd. nema smisla.
činjenica 2.
Za brze izračune bit će korisno naučiti tablicu kvadrata prirodni brojevi od \(1\) do \(20\) : \[\begin(array)(|ll|) \hline 1^2=1 & \quad11^2=121 \\ 2^2=4 & \quad12^2=144\\ 3^2=9 & \quad13 ^2=169\\ 4^2=16 & \quad14^2=196\\ 5^2=25 & \quad15^2=225\\ 6^2=36 & \quad16^2=256\\ 7^ 2=49 & \quad17^2=289\\ 8^2=64 & \quad18^2=324\\ 9^2=81 & \quad19^2=361\\ 10^2=100& \quad20^2= 400\\ \hline \end(niz)\]
činjenica 3.
Koje operacije možete izvesti s kvadratnim korijenom?
\(\metak\) Zbroj ili razlika kvadratnih korijena NIJE JEDNAK kvadratnom korijenu zbroja ili razlike, tj. \[\sqrt a\pm\sqrt b\ne \sqrt(a\pm b)\] Stoga, ako trebate izračunati, na primjer, \(\sqrt(25)+\sqrt(49)\) , tada prvo morate pronaći vrijednosti \(\sqrt(25)\) i \(\ sqrt(49)\ ) i zatim ih presavijte. Stoga, \[\sqrt(25)+\sqrt(49)=5+7=12\] Ako se vrijednosti \(\sqrt a\) ili \(\sqrt b\) ne mogu pronaći prilikom dodavanja \(\sqrt a+\sqrt b\), tada se takav izraz ne transformira dalje i ostaje takav kakav jest. Na primjer, u zbroju \(\sqrt 2+ \sqrt (49)\) možemo pronaći \(\sqrt(49)\) je \(7\) , ali \(\sqrt 2\) ne može se transformirati u bilo kako, eto zašto \(\sqrt 2+\sqrt(49)=\sqrt 2+7\). Nažalost, ovaj se izraz ne može dalje pojednostaviti\(\bullet\) Umnožak/kvocijent kvadratnih korijena jednak je kvadratnom korijenu umnoška/kvocijenta, tj. \[\sqrt a\cdot \sqrt b=\sqrt(ab)\quad \text(s)\quad \sqrt a:\sqrt b=\sqrt(a:b)\] (pod uvjetom da obje strane jednakosti imaju smisla)
Primjer: \(\sqrt(32)\cdot \sqrt 2=\sqrt(32\cdot 2)=\sqrt(64)=8\);
\(\sqrt(768):\sqrt3=\sqrt(768:3)=\sqrt(256)=16\);
\(\sqrt((-25)\cdot (-64))=\sqrt(25\cdot 64)=\sqrt(25)\cdot \sqrt(64)= 5\cdot 8=40\). \(\bullet\) Koristeći ova svojstva, zgodno je pronaći kvadratne korijene od veliki brojevi njihovim faktoriziranjem.
Pogledajmo primjer. Pronađimo \(\sqrt(44100)\) . Budući da \(44100:100=441\) , tada \(44100=100\cdot 441\) . Prema kriteriju djeljivosti broj \(441\) je djeljiv sa \(9\) (jer je zbroj njegovih znamenki 9 i djeljiv je sa 9), dakle \(441:9=49\), odnosno \(441=9\ cdot 49\) .
Tako smo dobili: \[\sqrt(44100)=\sqrt(9\cdot 49\cdot 100)= \sqrt9\cdot \sqrt(49)\cdot \sqrt(100)=3\cdot 7\cdot 10=210\] Pogledajmo još jedan primjer: \[\sqrt(\dfrac(32\cdot 294)(27))= \sqrt(\dfrac(16\cdot 2\cdot 3\cdot 49\cdot 2)(9\cdot 3))= \sqrt( \ dfrac(16\cdot4\cdot49)(9))=\dfrac(\sqrt(16)\cdot \sqrt4 \cdot \sqrt(49))(\sqrt9)=\dfrac(4\cdot 2\cdot 7)3 =\dfrac(56)3\]
\(\bullet\) Pokažimo kako se upisuju brojevi ispod znaka kvadratnog korijena na primjeru izraza \(5\sqrt2\) (kratki zapis za izraz \(5\cdot \sqrt2\)). Budući da \(5=\sqrt(25)\) , tada \
Imajte na umu također da npr.
1) \(\sqrt2+3\sqrt2=4\sqrt2\) ,
2) \(5\sqrt3-\sqrt3=4\sqrt3\)
3) \(\sqrt a+\sqrt a=2\sqrt a\) .
Zašto je to? Objasnimo na primjeru 1). Kao što već razumijete, ne možemo nekako transformirati broj \(\sqrt2\). Zamislimo da je \(\sqrt2\) neki broj \(a\) . Prema tome, izraz \(\sqrt2+3\sqrt2\) nije ništa više od \(a+3a\) (jedan broj \(a\) plus još tri ista broja \(a\)). I znamo da je to jednako četiri takva broja \(a\) , to jest \(4\sqrt2\) .
činjenica 4.
\(\bullet\) Često kažu "ne možete izvući korijen" kada se ne možete riješiti predznaka \(\sqrt () \ \) korijena (radikala) pri pronalaženju vrijednosti broja . Na primjer, možete uzeti korijen broja \(16\) jer \(16=4^2\) , dakle \(\sqrt(16)=4\) . Ali nemoguće je izvući korijen broja \(3\), odnosno pronaći \(\sqrt3\), jer ne postoji broj koji bi na kvadrat dao \(3\) .
Takvi brojevi (ili izrazi s takvim brojevima) su iracionalni. Na primjer, brojevi \(\sqrt3, \ 1+\sqrt2, \ \sqrt(15)\) i tako dalje. su iracionalni.
Iracionalni su i brojevi \(\pi\) (broj “pi”, približno jednak \(3,14\)), \(e\) (taj se broj naziva Eulerovim brojem, približno je jednak \(2,7 \)) itd.
\(\bullet\) Imajte na umu da će svaki broj biti ili racionalan ili iracionalan. A zajedno su svi racionalni i sve iracionalni brojevičine skup tzv skup realnih brojeva. Ovaj skup je označen slovom \(\mathbb(R)\) .
To znači da svi brojevi koji su na ovaj trenutak znamo da se zovu realni brojevi.
činjenica 5.
\(\bullet\) Modul realnog broja \(a\) je nenegativan broj \(|a|\) jednak udaljenosti od točke \(a\) do \(0\) na prava linija. Na primjer, \(|3|\) i \(|-3|\) jednaki su 3, jer su udaljenosti od točaka \(3\) i \(-3\) do \(0\) isti i jednak \(3 \) .
\(\bullet\) Ako je \(a\) nenegativan broj, tada \(|a|=a\) .
Primjer: \(|5|=5\) ; \(\qquad |\sqrt2|=\sqrt2\) . \(\bullet\) Ako je \(a\) negativan broj, tada \(|a|=-a\) .
Primjer: \(|-5|=-(-5)=5\) ; \(\qquad |-\sqrt3|=-(-\sqrt3)=\sqrt3\).
Kažu da za negativne brojeve modul “pojede” minus, dok pozitivne brojeve, kao i broj \(0\), modul ostavlja nepromijenjenima.
ALI Ovo pravilo vrijedi samo za brojeve. Ako ispod vašeg znaka modula stoji nepoznata \(x\) (ili neka druga nepoznata), na primjer, \(|x|\) , za koju ne znamo je li pozitivna, nula ili negativna, onda se riješite modula ne možemo. U ovom slučaju, ovaj izraz ostaje isti: \(|x|\) . \(\bullet\) Sljedeće formule vrijede: \[(\large(\sqrt(a^2)=|a|))\] \[(\large((\sqrt(a))^2=a)), \text( provided ) a\geqslant 0\] Vrlo često se napravi sljedeća greška: kažu da su \(\sqrt(a^2)\) i \((\sqrt a)^2\) jedno te isto. Ovo vrijedi samo ako je \(a\) pozitivan broj ili nula. Ali ako je \(a\) negativan broj, onda je to netočno. Dovoljno je razmotriti ovaj primjer. Uzmimo umjesto \(a\) broj \(-1\) . Tada \(\sqrt((-1)^2)=\sqrt(1)=1\) , ali izraz \((\sqrt (-1))^2\) uopće ne postoji (uostalom, nemoguće je koristiti znak korijena staviti negativne brojeve!).
Stoga vam skrećemo pozornost na činjenicu da \(\sqrt(a^2)\) nije jednako \((\sqrt a)^2\) ! Primjer: 1) \(\sqrt(\lijevo(-\sqrt2\desno)^2)=|-\sqrt2|=\sqrt2\), jer \(-\sqrt2<0\)
;
\(\fantom(00000)\) 2) \((\sqrt(2))^2=2\) . \(\bullet\) Budući da \(\sqrt(a^2)=|a|\) , tada \[\sqrt(a^(2n))=|a^n|\] (izraz \(2n\) označava paran broj)
To jest, kada se uzima korijen broja koji je na nekom stupnju, taj se stupanj prepolovljuje.
Primjer:
1) \(\sqrt(4^6)=|4^3|=4^3=64\)
2) \(\sqrt((-25)^2)=|-25|=25\) (imajte na umu da ako modul nije naveden, ispada da je korijen broja jednak \(-25\ ) ; ali zapamtimo da se po definiciji korijena to ne može dogoditi: kada izdvajamo korijen, uvijek bismo trebali dobiti pozitivan broj ili nulu)
3) \(\sqrt(x^(16))=|x^8|=x^8\) (budući da je svaki broj na parnu potenciju nenegativan)
činjenica 6.
Kako usporediti dva kvadratna korijena?
\(\bullet\) Za kvadratne korijene vrijedi: ako \(\sqrt a<\sqrt b\)
, то \(a
1) usporedi \(\sqrt(50)\) i \(6\sqrt2\) . Prvo, transformirajmo drugi izraz u \(\sqrt(36)\cdot \sqrt2=\sqrt(36\cdot 2)=\sqrt(72)\). Dakle, budući da \(50<72\)
, то и \(\sqrt{50}<\sqrt{72}\)
. Следовательно, \(\sqrt{50}<6\sqrt2\)
.
2) Između kojih cijelih brojeva se nalazi \(\sqrt(50)\)?
Budući da \(\sqrt(49)=7\) , \(\sqrt(64)=8\) i \(49<50<64\)
, то \(7<\sqrt{50}<8\)
, то есть число \(\sqrt{50}\)
находится между числами \(7\)
и \(8\)
.
3) Usporedimo \(\sqrt 2-1\) i \(0,5\) . Pretpostavimo da \(\sqrt2-1>0.5\) : \[\begin(aligned) &\sqrt 2-1>0,5 \ \big| +1\quad \text((dodajte jedan na obje strane))\\ &\sqrt2>0,5+1 \ \big| \ ^2 \quad\text((kvadriranje obje strane))\\ &2>1,5^2\\ &2>2,25 \end(poravnano)\] Vidimo da smo dobili netočnu nejednakost. Stoga je naša pretpostavka bila netočna i \(\sqrt 2-1<0,5\)
.
Imajte na umu da dodavanje određenog broja objema stranama nejednadžbe ne utječe na njezin predznak. Množenje/dijeljenje obje strane nejednakosti pozitivnim brojem također ne utječe na njen predznak, ali množenje/dijeljenje negativnim brojem mijenja predznak nejednakosti!
Možete kvadrirati obje strane jednadžbe/nejednadžbe SAMO AKO obje strane nisu negativne. Na primjer, u nejednadžbi iz prethodnog primjera možete kvadrirati obje strane, u nejednadžbi \(-3<\sqrt2\)
нельзя (убедитесь в этом сами)!
\(\bullet\) Treba zapamtiti da \[\početak(poravnano) &\sqrt 2\približno 1,4\\ &\sqrt 3\približno 1,7 \kraj(poravnano)\] Poznavanje približnog značenja ovih brojeva pomoći će vam pri uspoređivanju brojeva! \(\bullet\) Da biste izvukli korijen (ako se može izvući) iz nekog velikog broja koji nije u tablici kvadrata, prvo morate odrediti između kojih se “stotica” nalazi, zatim – između kojih “ desetice”, a zatim odredite posljednju znamenku tog broja. Pokažimo na primjeru kako to funkcionira.
Uzmimo \(\sqrt(28224)\) . Znamo da \(100^2=10\,000\), \(200^2=40\,000\), itd. Imajte na umu da je \(28224\) između \(10\,000\) i \(40\,000\) . Stoga je \(\sqrt(28224)\) između \(100\) i \(200\) .
Odredimo sada između kojih se “desetica” nalazi naš broj (to jest, na primjer, između \(120\) i \(130\)). Također iz tablice kvadrata znamo da \(11^2=121\) , \(12^2=144\) itd., zatim \(110^2=12100\) , \(120^2=14400 \ ) , \(130^2=16900\) , \(140^2=19600\) , \(150^2=22500\) , \(160^2=25600\) , \(170^2=28900 \ ) . Dakle, vidimo da je \(28224\) između \(160^2\) i \(170^2\) . Stoga je broj \(\sqrt(28224)\) između \(160\) i \(170\) .
Pokušajmo odrediti posljednju znamenku. Prisjetimo se koji jednoznamenkasti brojevi kada se kvadriraju na kraju daju \(4\)? To su \(2^2\) i \(8^2\) . Prema tome, \(\sqrt(28224)\) će završavati s 2 ili 8. Provjerimo ovo. Pronađimo \(162^2\) i \(168^2\) :
\(162^2=162\cdot 162=26224\)
\(168^2=168\cdot 168=28224\) .
Prema tome, \(\sqrt(28224)=168\) . Voila!
Da biste adekvatno riješili Jedinstveni državni ispit iz matematike, prvo morate proučiti teoretski materijal koji vas upoznaje s brojnim teoremima, formulama, algoritmima itd. Na prvi pogled može se činiti da je to prilično jednostavno. Međutim, pronalaženje izvora u kojem je teorija za Jedinstveni državni ispit iz matematike predstavljena na jednostavan i razumljiv način za učenike s bilo kojom razinom obrazovanja zapravo je prilično težak zadatak. Školski udžbenici ne mogu uvijek biti pri ruci. A pronalaženje osnovnih formula za jedinstveni državni ispit iz matematike može biti teško čak i na internetu.
Zašto je tako važno proučavati teoriju iz matematike ne samo za one koji polažu Jedinstveni državni ispit?
- Jer proširuje vaše horizonte. Proučavanje teorijskog gradiva iz matematike korisno je svima koji žele dobiti odgovore na širok raspon pitanja vezanih uz poznavanje svijeta oko sebe. Sve je u prirodi uređeno i ima jasnu logiku. Upravo se to ogleda u znanosti kroz koju je moguće razumjeti svijet.
- Jer razvija inteligenciju. Proučavajući referentne materijale za Jedinstveni državni ispit iz matematike, kao i rješavajući razne probleme, osoba uči razmišljati i logično zaključivati, kompetentno i jasno formulirati misli. Razvija sposobnost analize, generaliziranja i zaključivanja.
Pozivamo Vas da osobno procijenite sve prednosti našeg pristupa sistematizaciji i prezentaciji edukativnih materijala.

