Исключение левой рекурсии. Синтаксический анализ Удаление левой рекурсии онлайн

Определение. Правило вида $ называется аннулирующим правилом .

Управляющее устройство работает согласно правилам перехода , которые представляют алгоритм, реализуемый данной машиной Тьюринга. Каждое правило перехода предписывает машине, в зависимости от текущего состояния и наблюдаемого в текущей клетке символа, записать в эту клетку новый символ, перейти в новое состояние и переместиться на одну клетку влево или вправо. Некоторые состояния машины Тьюринга могут быть помечены как терминальные , и переход в любое из них означает конец работы, остановку алгоритма.

Машина Тьюринга называется детерминированной , если каждой комбинации состояния и ленточного символа в таблице соответствует не более одного правила. Если существует пара «ленточный символ - состояние», для которой существует 2 и более команд, такая машина Тьюринга называется недетерминированной .

начинающейся с и продолжающейся упомянутыми k терминалами.

Грамматика называется LL (k)-грамматикой, если она LL (k)- грамматика для некоторого k .

Пример 4.7 . Рассмотрим грамматику G = ({S, A, B}, {0, 1, a, b}, P, S) , где P состоит из правил

S -> A | B, A -> aAb | 0, B -> aBbb | 1.

Здесь . G не является LL (k)-грамматикой ни для какого k. Интуитивно, если мы начинаем с чтения достаточно длинной цепочки, состоящей из символов a , то не знаем, какое из правил S -> A и S -> B было применено первым, пока не встретим 0 или 1 .

Обращаясь к точному определению LL (k)-грамматики, положим и y = a k 1b 2k . Тогда выводы

соответствуют выводам (1) и (2) определения. Первые k символов цепочек x и y совпадают. Однако заключение ложно. Так как k здесь выбрано произвольно, то G не является LL -грамматикой.

Следствия определения LL(k)- грамматики

Теорема 4.6 . КС-грамматика является LL(k)-грамматикой тогда и только тогда, когда для двух различных правил и из Р пересечение пусто при всех таких , что .

Доказательство . Необходимость . Допустим, что и удовлетворяют условиям теоремы, а содержит x . Тогда по определению FIRST для некоторых y и z найдутся выводы

(Заметим, что здесь мы использовали тот факт, что N не содержит бесполезных нетерминалов, как это предполагается для всех рассматриваемых грамматик.) Если |x| < k ; то y = z = e . Так как , то G не LL (k)- грамматика .

Достаточность . Допустим, что G не LL (k)- грамматика .

Тогда найдутся такие два вывода

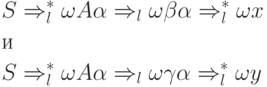
что цепочки x и y совпадают в первых k позициях, но . Поэтому и - различные правила из P и каждое из множеств и содержит цепочку FIRST k (x) , совпадающую с цепочкой FIRST k (y) .

Пример 4.8 . Грамматика G , состоящая из двух правил S -> aS | a , не будет LL (1)-грамматикой, так как

FIRST 1 (aS) = FIRST 1 (a) = a .

Интуитивно это можно объяснить так: видя при разборе цепочки, начинающейся символом a , только этот первый символ, мы не знаем, какое из правил S -> aS или S -> a надо применить к S . С другой стороны, G - это LL (2)- грамматика . В самом деле, в обозначениях только что представленной теоремы, если , то A = S и . Так как для S даны только два указанных правила, то и . Поскольку FIRST2(aS) = aa и FIRST2(a) = a , то по последней теореме G будет LL (2)-грамматикой.

Удаление левой рекурсии

Основная трудность при использовании предсказывающего анализа - это нахождение такой грамматики для входного языка, по которой можно построить таблицу анализа с однозначно определенными входами. Иногда с помощью некоторых простых преобразований грамматику, не являющуюся LL(1), можно привести к эквивалентной LL(1)-грамматике. Среди этих преобразований наиболее эффективными являются левая факторизация и удаление левой рекурсии . Здесь необходимо сделать два замечания. Во-первых, не всякая грамматика после этих преобразований становится LL(1), и, во-вторых, после таких преобразований получающаяся грамматика может стать менее понимаемой.

Непосредственную левую рекурсию, то есть рекурсию вида , можно удалить следующим способом. Сначала группируем A -правила:

где никакая из строк не начинается с A . Затем заменяем этот набор правил на

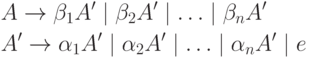
где A" - новый нетерминал. Из нетерминала A можно вывести те же цепочки, что и раньше, но теперь нет левой рекурсии . С помощью этой процедуры удаляются все непосредственные левые рекурсии , но не удаляется левая рекурсия, включающая два или более шага. Приведенный ниже алгоритм 4.8 позволяет удалить все левые рекурсии из грамматики.

Алгоритм 4.8 . Удаление левой рекурсии .

Вход . КС-грамматика G без e-правил (вида A -> e ).

Выход . КС-грамматика G" без левой рекурсии , эквивалентная G .

Метод . Выполнить шаги 1 и 2.

(1) Упорядочить нетерминалы грамматики G в произвольном порядке.

(2) Выполнить следующую процедуру:

После (i-1) -й итерации внешнего цикла на шаге 2 для любого правила вида , где k < i , выполняется s > k . В результате на следующей итерации (по i ) внутренний цикл (по j ) последовательно увеличивает нижнюю границу по m в любом правиле , пока не будет m >= i . Затем, после удаления непосредственной левой рекурсии для A i -правил, m становится больше i .

Грамматика, содержащая левую рекурсию, не является LL(1)- грамматикой. Рассмотрим правила

A → Aa (левая рекурсия в A)

A → a

Здесь a символ-предшественник для обоих вариантов нетерминала A . Аналогично грамматика, содержащая левый рекурсивный цикл, не может быть LL(1)-грамматикой, например

A → BC

B → CD

C → AE

Грамматику, содержащую левый рекурсивный цикл, можно преобразовать в грамматику, содержащую только прямую левую рекурсию, и далее, за счет введения дополнительных нетерминалов, левую рекурсию можно исключить полностью (в действительности она заменяется правой рекурсией, которая не представляет проблемы в отношении LL(1)-свойства).

В качестве примера рассмотрим грамматику с порождающими правилами

S → Aa

A → Bb

B → Cc

C → Dd

C → e

D → Az

которая имеет левый рекурсивный цикл, вовлекающий A, B, C, D . Чтобы заменить этот цикл прямой левой рекурсией, упорядочим нетерминалы следующим образом: S, A, B, C, D .

Рассмотрим все порождающие правила вида

Xi → Xj γ,

где Xi и Xj – нетерминалы, а γ – строка терминальных и нетерминальных символов. В отношении правил, для которых j ≥ i , никакие действия не производятся. Однако это неравенство не может выдерживаться для всех правил, если есть левый рекурсивный цикл. При выбранном нами порядке мы имеем дело с единственным правилом:

D → Az

так как A предшествует D в этом упорядочении. Теперь начнем замещать A , пользуясь всеми правилами, имеющими A в левой части. В результате получаем

D → Bbz

Поскольку B предшествует D в упорядочении, процесс повторяется, что дает правило:

D → Ccbz

Затем он повторяется еще раз и дает два правила:

D → ecbz

D → Ddcbz

Теперь преобразованная грамматика выглядит следующим образом:

S → Aa

A → Bb

B → Cc

C → Dd

C → e

D → Ddcbz

D → ecbz

Все эти порождающие правила имеют требуемый вид, а левый рекурсивный цикл заменен прямой левой рекурсией. Чтобы исключить прямую левую рекурсию, введем новый нетерминальный символ Z и заменим правила

D → ecbz

D → Ddcbz

D → ecbz

D → ecbzZ

Z → dcbz

Z → dcbzZ

Заметим, что до и после преобразования D генерирует регулярное выражение

(ecbz) (dcbz)*

Обобщая, можно показать, что если нетерминал A появляется в левых частях r + s порождающих правил, r из которых используют прямую левую рекурсию, а s – нет, т.е.

A → Aα 1, A → Aα 2,..., A → Aα r

A → β 1, A → β 2,..., A → β s

то эти правила можно заменить на следующие:

Неформальное доказательство заключается в том, что до и после преобразования A генерирует регулярное выражение (β 1 | β 2 |... | β s) (α 1 | α 2 |... | α r) *

Следует обратить внимание, что устранив левую рекурсию (или левый рекурсивный цикл), мы еще не получаем LL(1)-грамматику, т.к. для некоторых нетерминалов в левой части правил полученных грамматик существуют альтернативные правые части, начинающиеся с одних и тех же символов. Поэтому после устранения левой рекурсии следует продолжить преобразование грамматики к LL(1) виду.

17.Преобразование грамматик в LL(1) форму. Факторизация .

Факторизация

Во многих ситуациях грамматики, не обладающие признаком LL(1), можно преобразовать в LL(1)-грамматики с помощью процесса факторизации. Рассмотрим пример такой ситуации.

P → begin D ; С end

D → d , D

D → d

С → s ; С

С → s

В процессе факторизации мы заменяем несколько правил для одного нетерминала в левой части, правая часть которых начинается с одного и того же символа (цепочки символов) на одно правило, где в правой части за общим началом следует дополнительно вводимый нетерминал. Также грамматика дополняется правилами для дополнительного нетерминала, согласно которым из него выводятся различные «остатки» первоначальной правой части правила. Для приведенной выше грамматики это даст следующую LL(1)-грамматику:

P → begin D ; С end

D → d X X )

X → , D (по 1-му правилу для D исходной грамматики за d следует, D )

X → ε (по 2-му правилу для D исходной грамматики за d ничего нет (пустая строка))

С → s Y (вводим дополнительный нетерминал Y )

Y → ; С (по 1-му правилу для C исходной грамматики за s следует; C )

Y → ε (по 2-му правилу для C исходной грамматики за s ничего нет (пустая строка))

Аналогичным образом, порождающие правила

S → aSb

S → aSc

S → ε

можно преобразовать путем факторизации в правила

S → aSX

S → ε

X → b

X → c

и полученной в результате грамматикой будет LL(1). Процесс факторизации, однако, нельзя автоматизировать, распространив его на общий случай. Следующий пример показывает, что может произойти. Рассмотрим правила

1. P → Qx

2. P → Ry

3. Q → sQm

4. Q → q

5. R → sRn

6. R → r

Оба множества направляющих символов для двух вариантов P содержат s , и, пытаясь "вынести s за скобки", мы замещаем Q и R в правыхчастях правил 1 и 2:

P → sQmx

P → sRny

P → qx

P → ry

Эти правила можно заменить следующими:

P → qx

P → ry

P → sP 1

P 1 → Qmx

P 1 → Rny

Правила для P1 аналогичны первоначальным правилам для P и имеют пересекающиеся множества направляющих символов. Мы можем преобразовать эти правила так же, как и правила для P :

P 1 → sQmmx

P 1 → qmx

P 1 → sRnny

P 1 → rny

Факторизуя, получаем

При процедуре рекурсивного разбора сверху вниз может возникнуть проблема бесконечного цикла.

В грамматике для арифметических операций применение второго правила приведет к зацикливанию процедуры разбора. Подобные грамматики называются леворекурсивными. Грамматика называется леворекурсивной, если в ней существует нетерминал А, для которого существует вывод А=>+Аa. В простых случаях левая рекурсия вызвана правилами вида

В этом случае вводят новый нетерминал и исходные правила заменяют следующими.

(если есть нетерминал А, для которого существует вывод А→+Аa за 1 или более шагов). Левой рекурсии можно избежать, преобразовав грамматику.

Например, продукции A→Aa

Можно заменить на эквивалентные:

Для такого случая существует алгоритм, исключающий левую рекурсию:

1) определяем на множестве нетерминалов какой-либо порядок (А 1 , А 2 , …, А n)

2) берем каждый нетерминал, если для него есть продукция, учитывающая нетерминал, стоящий левее, и преобразуем грамматику:

for i:=1 to n do

for j:=1 to i-1 do

if Ai → Ajγ then Ai→δ1γ

│ δkγ, где

Aj → δ1│ δ2│ …│ δk

3) исключаем все случаи непосредственной левой рекурсии (правило1)

Т.о. алгоритм помогает избежать зацикливания.

Исключение левой рекурсии из грамматики арифметических выражений и общий вид правила исключения левой рекурсии:

Общий вид правила исключения левой рекурсии

Левая факторизация.

LL(1)-грамматики нужны для того, чтобы выбрать нужную продукцию для разбора сверху-вниз, чтобы не произошло зацикливание.

Иногда существует возможность преобразовать грамматику к LL(1) виду, используя метод левой факторизации.

Например: S→ if B then S

│if B then S else S

Эти продукции нарушают условие LL(1)-грамматик. Эту грамматику можно преобразовать к виду LL(1).

S → if B then S Tail

В общем виде это преобразование можно определить так:

вводим новый нетерминал В, для которого

| β N Для B можно применить левую факторизацию. Эта процедура повторяется, пока остается неопределенным выбор продукции (т.е. пока в ней можно что-нибудь изменить).

Построение множества FIRST

Множество First для нетерминала определяет множество терминалов, с которых может начинаться данный нетерминал.

1. Если х - терминал, то first(x)={x}. Так как первым символом последовательности из одного терминала может являться только сам терминал.

2. Если в грамматике присутствует правило Хà e, то множество first(х) включает e. Это означает, что Х может начинаться с пустой последовательности, то есть отсутствовать вообще.

3. Для всех продукций вида XàY1 Y2 … Yk выполняем следующее. Добавляем в множество first(Х) множество first(Yi) до тех пор, пока first(Yi-1) содержит e, а first(Yi) не содержит e. При этом i изменяется от 0 до k. Это необходимо, так как если Yi-1 может отсутствовать, то необходимо выяснить, с чего будет начинаться вся последовательность в этом случае.

LL(k)-свойство накладывает большие ограничения на грамматику. Иногда имеется возможность преобразовать грамматику так, чтобы получившаяся грамматика обладала свойством LL(1) . Такое преобразование далеко не всегда удается, но если удалось получить LL(1)-грамматику, то для построения анализатора можно использовать метод рекурсивного спуска без возвратов.

Предположим, что необходимо построить анализатор языка, порождаемого следующей грамматикой:

E → E + T | E – T | T

T → T * F | T / F | F

F → num | (E )

Терминалы множества FIRST(T) принадлежат также множеству FIRST(E+T) , поэтому нельзя однозначно определить последовательность вызовов процедур, которую необходимо выполнить при анализе входной цепочки. Проблема заключается в том, что нетерминал E встречается на первой позиции правой части правила, левая часть которого также E . В такой ситуации нетерминал E называется непосредственно леворекурсивным.

Нетерминал A КС-грамматики G называется леворекурсивным , если в грамматике существует вывод A =>* Aw .

Грамматика, имеющая хотя бы одно леворекурсивное правило, не может быть LL(1) -грамматикой.

С другой стороны, известно, что каждый КС-язык определяется хотя бы одной нелеворекурсивной грамматикой.

1. Алгоритм устранения леворекурсивности

Пусть G = (N, T, P, S) – КС-грамматика и правило A→Aw 1 | Aw 2 | … | Aw n | v 1 | v 2 | … | v m представляет собой все правила из P , содержащие A в левой части, причем ни одна из цепочек v i не начинается с нетерминала A .

Добавим к множеству N еще один нетерминал A" и заменим правила, содержащие A в левой части, на следующие:

A → v 1 | v 2 | … | v m | v 1 A’ | v 2 A’ | … | v m A"

A’ → w 1 | w 2 | … | w n | w 1 A’ | w 2 A’ | … | w n A"

Можно доказать, что полученная грамматика эквивалентна исходной.

В результате применения этого преобразования к приведенной выше грамматике, описывающей арифметические выражения, получим следующую грамматику:

E → T | TE "

E " → + T | + TE "

T → F | FT "

T "→ * F | * FT "

F → (E ) | num

Нетрудно показать, что получившаяся грамматика обладает свойством LL(1) .

Еще одна подобная проблема связана с тем, что два правила для одного и того же нетерминала начинаются одними и теми же символами.

Например,

S → if E then S else S

S → if E then S

В этом случае добавим еще один нетерминал, который будет соответствовать различным окончаниям этих правил. Получим следующие правила:

S → if E then S S ’

S " →

S "→ else S

Для полученной грамматики может быть реализован метод рекурсивного спуска.

1. 9.1.4. Рекурсивный спуск с возвратами.

Для того, чтобы иметь возможность применить метод рекурсивного спуска, необходимоы 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 преобразовать грамматику к виду, в котором множества FIRST не пересекаются, что является сложным процессом, поэтому на практике используется прием, называемый рекурсивным спуском с возвратами .

Для этого лексический анализатор представляется в виде объекта, у которого помимо традиционных методов scan , next и т. д., есть также копирующий конструктор. Затем во всех ситуациях, где может возникнуть неоднозначность, перед началом разбора надо запомнить текущее состояние лексического анализатора (т. е. сделать копию лексического анализатора) и продолжить разбор текста, считая, что имеем дело с первой из возможных в данной ситуации конструкций. Если этот вариант разбора заканчивается неудачей, то надо восстановить состояние лексического анализатора и пытаться заново разобрать тот же самый фрагмент с помощью следующего варианта грамматики и т. д. Если все варианты разбора заканчиваются неудачно, то сообщается об ошибке.

Такой метод разбора потенциально медленнее, чем рекурсивный спуск без возвратов, но в данном случае удается сохранить грамматику в ее оригинальном виде и сэкономить усилия программиста.