Как прибавить числа с разными знаками. Сложение и вычитание целых чисел

формирование знаний о правиле сложения чисел с разными знаками, умений применять его в простейших случаях;

развитие умений сравнивать, выявлять закономерности, обобщать;

воспитание ответственного отношения к учебному труду.

Оборудование: мультимедийный проектор, экран.

Тип урока: урок изучения нового материала.

ХОД УРОКА

1.Организационный момент.

Ровно встали,

Тихо сели.

Прозвенел сейчас звонок,

Начинаем наш урок.

Ребята! Сегодня к нам на урок пришли гости. Давай повернемся к ним и улыбнемся друг другу. Итак, мы начинаем наш урок.

Слайд 2 — Эпиграф урока: «Кто ничего не замечает, тот ничего не изучает.

Кто ничего не изучает, тот вечно хнычет и скучает.»

Роман Сеф (детский писатель)

Слад 3 — Предлагаю поиграть в игру «Наоборот». Правила игры: нужно разделить слова на две группы: выигрыш, ложь,тепло, отдал, правда, добро, проигрыш, взял, зло, холодно, положительное, отрицательное.

Противоречий в жизни много. С их помощью мы определяем окружающую действительность. Для нашего занятия мне необходимо последнее: положительное – отрицательное.

О чем мы говорим в математике, когда употребляем эти слова? (О числах.)

Великий Пифагор утверждал: «Числа правят миром». Я предлагаю поговорить о самых загадочных числах в науке – о числах с разными знаками. — Отрицательные числа появились в науке, как противоположность к положительным. Их путь в науку был труден, потому что даже многие ученые не поддерживали идей об их существовании.

Какие понятия и величины люди измеряют положительными и отрицательными числами? (заряды элементарных частиц, температуру, убытки, высоту и глубину и т.д.)

Слайд 4- Слова противоположные по значению – антонимы (таблица).

2.Постановка темы урока.

Слайд 5(работа с таблицей) – Какие числа изучали на предыдущих уроках? – Какие задания, связанные с положительными и отрицательными числами вы умеете выполнять? – Внимание на экран. (Слайд 5)– Какие числа представлены в таблице?– Назовите модули чисел, записанных по горизонтали. – Укажите наибольшее число, укажите число с наибольшим модулем.– Ответьте на те же вопросы для чисел, записанных по вертикали.– Всегда ли наибольшее число и число с наибольшим модулем совпадают?– Найдите сумму положительных чисел, сумму отрицательных чисел.– Сформулируйте правило сложения положительных чисел и правило сложения отрицательных чисел.– Какие числа осталось сложить? – Умеете ли вы их складывать? – Знаете ли вы правило сложения чисел с разными знаками? – Сформулируйте тему урока.– Какую цель вы перед собой поставите? .Подумайте, что мы будем делать сегодня? (Ответы детей). Сегодня мы продолжаем знакомиться с положительными и отрицательными числами. Тема нашего урока “Сложение чисел с разными знаками.” А наша цель: научиться без ошибок, складывать числа с разными знаками. Записали в тетрадь число и тему урока.

3.Работа по теме урока.

Слайд 6. – Применяя данные понятия, найдите результаты сложения чисел с разными знаками на экране.– Какие числа являются результатом сложения положительных чисел, отрицательных чисел? – Какие числа являются результатом сложения чисел с разными знаками? – От чего зависит знак суммы чисел с разными знаками? (Слайд 5)– От слагаемого с наибольшим модулем.– Это как при перетягивании каната. Побеждает сильнейший.

Слайд 7 – Поиграем. Представьте, что вы перетягиваете канат..Учитель. Соперники обычно встречаются на соревнованиях. И мы сегодня побываем с вами на нескольких турнирах. Первое, что нас ждет – это финал конкурса по перетягиванию каната. Встречаются Иван Минусов под номером -7 и Петр Плюсов под номером +5. Как вы думаете, кто победит? Почему? Итак, победил Иван Минусов, он действительно оказался сильнее соперника, и смог перетащить его на свою отрицательную сторону ровно на два шага.

Слайд 8.- .А теперь побываем на других соревнованиях. Перед вами финал состязания по стрельбе. Лучшими в этом виде оказались Минус Тройкин с тремя воздушными шарами и Плюс Четвериков, имеющий в запасе четыре воздушных шарика. А здесь ребята, как вы думаете, кто станет победителем?

Слайд 9— Соревнования показали, что в них побеждает сильнейший. Так и при сложении чисел с разными знаками: -7 + 5 = -2 и -3 + 4 = +1. Ребята, как же складываются числа с разными знаками?Учащиеся предлагают свои варианты.

Учитель формулирует правило, приводит примеры.

10 + 12 = +(12 – 10) = +2

4 + 3,6 = -(4 – 3,6) = -0,4

Учащиеся в процессе демонстрации могут комментировать решение, появляющееся на слайде.

Слайд 10— Учитель- поиграем ещё в одну игру «Морской бой». К нашему побережью приближается вражеский корабль, его необходимо подбить и потопить. Для этого у нас есть пушка. Но чтобы попасть в цель необходимо произвести точные расчеты. Какие вы сейчас увидите. Готовы? Тогда вперед! Прошу не отвлекаться, примеры меняются ровно через 3 сек. Все готовы?

Учащиеся по очереди выходят к доске и вычисляют примеры, появляющиеся на слайде. – Назовите этапы выполнения задания.

Слайд 11-Работа по учебнику: стр.180 п.33 , прочитать правило сложения чисел с разными знаками. Комментирует правило.– В чём отличие правила, предложенного в учебнике, от составленного вами алгоритма? Рассмотреть примеры в учебнике с комментарием.

Слайд 12-Учитель-А теперь ребята давайте проведем эксперимент. Но не химический, а математический! Возьмем числа 6 и 8, знаки плюс и минус и все хорошенько перемешаем. Получим четыре примера-опыта. Проделайте их у себя в тетради.(двое учащихся решают на крыльях доски, затем ответы проверяются). Какие выводы можно сделать из этого эксперимента?(Роль знаков).Проведем ещё 2 эксперимента, но с вашими числами (выходят по1 человеку к доске). Придумаем друг другу числа и проверим результаты эксперимента (взаимопроверка).

Слайд 13.- На экран выводится правило в стихотворной форме.

4.Закрепление темы урока.

Слайд 14 –Учитель- «Знаки всякие нужны, знаки всякие важны!» Сейчас, ребята, мы поделимся с вами на две команды. Мальчики будут в команде Деда Мороза, а девочки – Солнышка. Ваша задача, не вычисляя примеры, определить в каких из них получатся отрицательные ответы, а в каких — положительные и выписать в тетрадь буквы этих примеров. Мальчики соответственно – отрицательные, а девочки – положительные(выдаются карточки с приложения). Проводится самопроверка.

Молодцы! Чутьё на знаки у вас отличное. Это поможет вам выполнить следующее задание

Слайд 15 — Физкульминутка. -10, 0,15,18,-5,14,0,-8,-5 и т. д.(отрицательные числа- приседают, положительные числа- подтягиваются вверх, подпрыгивают)

Слайд 16-Решить 9 примеров самостоятельно (задание на карточках в приложении). 1человек у доски. Сделать самопроверку.Ответы выводятся на экран, ошибки учащиеся исправляют в тетради. Поднимите руки, у кого верно. (Отметки выставляются только за хороший и отличный результат)

Слайд 17 -Правильно решать примеры нам помогают правила. Давайте их повторим На экране алгоритм сложения чисел с разными знаками.

5.Организация самостоятельной работы.

Слайд 18 -Фронтальная работа через игру «Отгадай слово»(задание на карточках в приложении) .

Слайд 19 — Должна получиться оценка за игру — «пятёрочка»

Слайд 20 -Атеперь,внимание. Домашнее задание. Домашнее задание не должно вызвать у вас затруднений.

Слайд 21 —Законы сложения в физических явлениях. Придумайте примеры на сложение чисел с разными знаками и задайте их друг другу. Что нового вы узнали? Достигли ли мы поставленной цели?

Слайд 22 —Вот и кончился урок,подведем сейчас итог. Рефлексия. Учитель комментирует и выставляет оценки за урок.

Слайд 23 — Спасибо за внимание!

Желаю вам, чтобы в вашей жизни было больше положительного и меньше отрицательного, Хочу сказать вам, ребята, спасибо за вашу активную работу. Я думаю, что вы легко сможете применить полученные знания на последующих уроках. Урок окончен. Всем большое спасибо. До свидания!

Сложение отрицательных чисел.

Сумма отрицательных чисел есть число отрицательное. Модуль суммы равен сумме модулей слагаемых.

Давайте разберемся, почему же сумма отрицательных чисел будет тоже отрицательным числом. Поможет нам в этом координатная прямая, на которой мы выполним сложение чисел -3 и -5. Отметим на координатной прямой точку, соответствующее числу -3.

К числу -3 нам нужно прибавить число -5. Куда мы пойдем от точки, соответствующей числу -3? Правильно, влево! На 5 единичных отрезков. Отмечаем точку и пишем число ей соответствующее. Это число -8.

Итак, при выполнении сложения отрицательных чисел с помощью координатной прямой мы все время находимся слева от начала отсчета, поэтому, понятно, что результат сложения отрицательных чисел есть число тоже отрицательное.

Примечание. Мы складывали числа -3 и -5, т.е. находили значение выражения -3+(-5). Обычно при сложении рациональных чисел просто записывают эти числа с их знаками, как бы перечисляют все числа, которые нужно сложить. Такую запись называют алгебраической суммой. Применяют (в нашем примере) запись: -3-5=-8.

Пример. Найти сумму отрицательных чисел: -23-42-54. (Согласитесь, что эта запись короче и удобнее вот такой: -23+(-42)+(-54))?

Решаем по правилу сложения отрицательных чисел: складываем модули слагаемых: 23+42+54=119. Результат будет со знаком «минус».

Записывают обычно так: -23-42-54=-119.

Сложение чисел с разными знаками.

Сумма двух чисел с разными знаками имеет знак слагаемого с большим модулем. Чтобы найти модуль суммы, нужно из большего модуля вычесть меньший.

Выполним сложение чисел с разными знаками с помощью координатной прямой.

1) -4+6. Требуется к числу -4 прибавить число 6. Отметим число -4 точкой на координатной прямой. Число 6 — положительное, значит от точки с координатой -4 нам нужно идти вправо на 6 единичных отрезков. Мы оказались справа от начала отсчета (от нуля) на 2 единичных отрезка.

Результат суммы чисел -4 и 6 — это положительное число 2:

— 4+6=2. Как можно было получить число 2? Из 6 вычесть 4, т.е. из большего модуля вычесть меньший. У результата тот же знак, что и у слагаемого с большим модулем.

2) Вычислим: -7+3 с помощью координатной прямой. Отмечаем точку, соответствующую числу -7. Идем вправо на 3 единичных отрезка и получаем точку с координатой -4. Мы были и остались слева от начала отсчета: ответ — отрицательное число.

— 7+3=-4. Этот результат мы могли получить так: из большего модуля вычли меньший, т.е. 7-3=4. В результате поставили знак слагаемого, имеющего больший модуль: |-7|>|3|.

Примеры. Вычислить: а) -4+5-9+2-6-3; б) -10-20+15-25.

План урока:

I. Организационный момент

Проверка индивидуального домашнего задания.

II. Актуализация опорных знаний учащихся

1. Взаимотренаж. Контрольные вопросы (парнаяорганизационная форма работы – взаимопроверка). 2. Устная работа с комментированием (групповаяорганизационная форма работы).3. Самостоятельная работа (индивидуальнаяорганизационная форма работы, самопроверка).

III. Сообщение темы урока

Групповая организационная форма работы,выдвижение гипотезы, формулирование правила.

1. Выполнение тренировочных заданий по учебнику(групповая организационная форма работы).2. Работа сильных обучающихся по карточкам(индивидуальная организационная форма работы).

VI. Физпауза

IX. Домашнее задание.

Цель: формирование навыка сложениячисел с разными знаками.

Задачи:

• Сформулировать правило сложения чисел с разными знаками.
• Отрабатывать умение складывать числа с разными знаками.
• Развивать логическое мышление.
• Воспитывать умение работать в паре, взаимоуважение.

Материал к уроку:карточки длявзаимотренажа, таблицы результатов работы,индивидуальные карточки на повторение изакрепление материала, девиз для индивидуальнойработы, карточки с правилом.

ХОД УРОКА

I. Организационный момент

– Начнём урок с проверкииндивидуального домашнего задания. Девизомнашего урока будут слова Яна Амоса Каменского.Дома вам нужно было подумать над его словами. Каквы его понимаете? («Считай несчастным тот деньили тот час, в который ты не усвоил ничего новогои ничего не прибавил к своему образованию»)–Как вы понимаете слова автора? (Если мыне узнаём ничего нового, не получаем новыезнания, то этот день можно считать пропавшим илинесчастным. Надо стремиться к получению новыхзнаний).– И сегодняшний день не будет несчастным потому,что мы опять будем узнавать что-то новое.

II. Актуализация опорных знанийучащихся

– Для того чтобы изучать новый материал, надоповторить пройденный. Дома было задание – повторить правила и сейчасвы покажете свои знания, поработав сконтрольными вопросами.

(Контрольные вопросы по теме «Положительные иотрицательные числа»)

Работа в паре. Взаимопроверка. Результатыработы отмечают в таблице)

Как называются числа расположенные справа от начала координат? ПоложительныеКакие числа называют противоположными? Два числа, отличающиеся друг от друга только знаками, называют противоположнымиЧто называют модулем числа? Расстояние от точки А(а) до начала отсчёта, т. е. до точки О(0), называют модулем числаКак обозначают модуль числа? Прямыми скобкамиСформулируй правило сложения отрицательных чисел? Чтобы сложить два отрицательных числа надо: сложить их модули и поставить знак минусКак называются числа расположенные слева от начала координат? ОтрицательныеКакое число противоположно нулю? 0Может ли модуль какого-нибудь числа быть отрицательным числом? Нет. Расстояние не бывает отрицательнымНазови правило сравнения отрицательных чисел Из двух отрицательных чисел больше то, модуль которого меньше и меньше то, у которого модуль большеЧему равна сумма противоположных чисел? 0

Ответы на вопросы «+» правильно, «–»неправильно Критерии оценки: 5 – «5»; 4 – «4»;3 – «3»

1 2 3 4 5 ОценкаК/вопросы Сам/работа Инд/ работа Итог

– Какие вопросы были наиболее трудными?– Что нужно для успешной сдачи контрольныхвопросов? (Знать правила)

2. Устная работа с комментированием

– 45 + (– 45) = (– 90) – 100 + (– 38) = (– 138) – 3, 5 + (–2, 4) = (– 5,9) – 17/70 + (– 26/70) = (– 43/70) – 20 + (– 15) = (– 35)

– Какие знания вам были нужны для решения 1-5примеров?

3. Самостоятельная работа

– 86, 52 + (– 6, 3) = – 92,82– 49/91 + (– 27/91) = – 76/91– 76 + (– 99) = – 175– 14 + (– 47) = – 61– 123,5 + (– 25, 18) = – 148,686 + (– 10) =

(Самопроверка. Открыть во время проверкиответы)

– Почему последний пример вызвал у васзатруднение? – Сумму каких чисел нужно найти, а сумму какихчисел мы знаем, как находить?

III. Сообщение темы урока

– Сегодня на уроке мы узнаем правило сложениячисел с разными знаками. Будем учитьсяскладывать числа с разными знаками.Самостоятельная работа в конце урока покажетваши успехи.

IV. Изучение нового материала

– Откроем тетради, запишем дату, класснаяработа, тему урока «Сложение чисел с разнымизнаками».– Что изображено на доске? (Координатнаяпрямая)

– Докажите, что это координатная прямая? (Естьначало отсчёта, направление отсчёта, единичныйотрезок)– Сейчас мы с вами вместе будем учитьсяскладывать числа с разными знаками с помощьюкоординатной прямой.

(Объяснение обучающихся под руководствомучителя.)

– Найдём на координатной прямой число 0. К 0 надоприбавить число 6. Делаем 6 шагов в правую сторонуот начала координат, т.к. число 6 – положительное(ставим цветной магнитик на получившееся число 6).К 6 прибавим число (– 10), делаем 10 шагов в левуюсторону от начала координат, т. к. (– 10) числоотрицательное (ставим цветной магнитик наполучившееся число (– 4).)– Какой получили ответ? (– 4) – Как получили число 4? (10 – 6) Сделайте вывод: Из числа с большим модулем вычличисло с меньшим модулем. – Как в ответе получили знак минус?Сделайте вывод: Взяли знак у числа с большиммодулем.– Запишем пример в тетрадь:

6 + (–10) = – (10 – 6) = – 4 10 + (–3) = + (10 – 3) = 7 (Аналогично решаем)

Принята запись:

6 + (– 10) = – (10 – 6) = – 4 10 + (– 3) = + (10 – 3) = 7

– Ребята, вы сейчас сами сформулировалиправило сложения чисел с разными знаками. Вашипредположения мы назовём гипотезой. Вывыполнили очень важную интеллектуальную работу.Подобно учёным выдвинули гипотезу и открылиновое правило. Сверим вашу гипотезу с правилом(листок с отпечатанным правилом лежит на парте).Прочитаем хором правило сложения чисел сразными знаками

– Правило очень важное! Оно позволяет сложитьчисла разных знаков без помощи координатнойпрямой.– Что не понятно?– Где можно сделать ошибку?– Для того чтобы правильно и без ошибоквычислять задания с положительными иотрицательными числами, надо знать правила.

V. Закрепление изученного материала

– Сможете ли вы найти сумму этих чисел накоординатной прямой? – С помощью координатной прямой такой примеррешить трудно, поэтому будем использовать прирешении открытое вами правило.Задание написано на доске:Учебник – с. 45; № 179 (в, г); № 180 (а, б); № 181 (б, в)(Сильный ученик работает на закрепление даннойтемы с дополнительной карточкой.)

VI. Физпауза(Выполняют стоя)

– Человек обладает положительными иотрицательными качествами. Распределите этикачества на координатной прямой.(Положительные качества – справа от началаотсчёта, отрицательные – слева от началаотсчёта.)– Если качество отрицательное – хлопаем одинраз, положительное – два раза. Будьтевнимательны!– Доброта, злость, жадность, взаимовыручка,взаимопонимание, грубость, и, конечно же, силаволи и стремление к победе, которыевам сейчас потребуются, так как впереди у вассамостоятельная работа)VII. Индивидуальная работа с последующейвзаимопроверкой

Вариант 1 Вариант 2– 100 + (20) = – 100 + (30) =100 + (– 20) = 100 + (– 30) =56 + (– 28) = 73 + (– 28) =4,61 + (– 2,2) = 5, 74 + (– 3,15) =– 43 + 65 = – 43 + 35 =

Индивидуальная работа (для сильныхобучающихся) с последующей взаимопроверкой

Вариант 1 Вариант 2– 100 + (20) = – 100 + (30) =100 + (– 20) = 100 + (– 30) =56 + (– 28) = 73 + (– 28) =4,61 + (– 2,2) = 5, 74 + (– 3,15) =– 43 + 65 = – 43 + 35 =100 + (– 28) = 100 + (– 39) =56 + (– 27) = 73 + (– 24) =– 4,61 + (– 2,22) = – 5, 74 + (– 3,15) =– 43 + 68 = – 43 + 39 =

VIII. Подведение итогов урока. Рефлексия

– Я считаю, что вы поработали активно,старательно, участвовали в открытии новыхзнаний, высказывали свое мнение, сейчас я могуоценить вашу работу.– Скажите, ребята, что эффективнее: получатьготовую информацию или размышлять самим?– Что нового мы узнали на уроке? (Научилисьскладывать числа с разными знаками.)– Назовите правило сложения чисел с разнымизнаками.– Скажите, наш урок сегодня не зря прошёл?– Почему? (Получили новые знания.)– Вернемся к девизу. Значит, Ян Амос Каменскийбыл прав, когда сказал: «Считай несчастным тотдень или тот час, в который ты не усвоил ничегонового и ничего не прибавил к своемуобразованию».

IX. Домашнее задание

Выучить правило (карточка), с.45, №184.Индивидуальное задание – как вы понимаете словаРоджера Бэкона: «Человек, не знающийматематику, не способен ни к каким другим наукам.Более того, он даже не способен оценить уровеньсвоего невежества?

Дроби — это обычные числа, их тоже можно складывать и вычитать. Но из-за того, что в них присутствует знаменатель, здесь требуются более сложные правила, нежели для целых чисел.

Рассмотрим самый простой случай, когда есть две дроби с одинаковыми знаменателями. Тогда:

Чтобы сложить дроби с одинаковыми знаменателями, надо сложить их числители, а знаменатель оставить без изменений.

Чтобы вычесть дроби с одинаковыми знаменателями, надо из числителя первой дроби вычесть числитель второй, а знаменатель опять же оставить без изменений.

Внутри каждого выражения знаменатели дробей равны. По определению сложения и вычитания дробей получаем:

Как видите, ничего сложного: просто складываем или вычитаем числители — и все.

Но даже в таких простых действиях люди умудряются допускать ошибки. Чаще всего забывают, что знаменатель не меняется. Например, при сложении их тоже начинают складывать, а это в корне неправильно.

Избавиться от вредной привычки складывать знаменатели достаточно просто. Попробуйте сделать то же самое при вычитании. В результате в знаменателе получится ноль, и дробь (внезапно!) потеряет смысл.

Поэтому запомните раз и навсегда: при сложении и вычитании знаменатель не меняется!

Также многие допускают ошибки при сложении нескольких отрицательных дробей. Возникает путаница со знаками: где ставить минус, а где — плюс.

Эта проблема тоже решается очень просто. Достаточно вспомнить, что минус перед знаком дроби всегда можно перенести в числитель — и наоборот. Ну и конечно, не забывайте два простых правила:

1. Плюс на минус дает минус;
2. Минус на минус дает плюс.

Разберем все это на конкретных примерах:

Задача. Найдите значение выражения:

В первом случае все просто, а во втором внесем минусы в числители дробей:

Что делать, если знаменатели разные

Напрямую складывать дроби с разными знаменателями нельзя. По крайней мере, мне такой способ неизвестен. Однако исходные дроби всегда можно переписать так, чтобы знаменатели стали одинаковыми.

Существует много способов преобразования дробей. Три из них рассмотрены в уроке «Приведение дробей к общему знаменателю », поэтому здесь мы не будем на них останавливаться. Лучше посмотрим на примеры:

Задача. Найдите значение выражения:

В первом случае приведем дроби к общему знаменателю методом «крест-накрест». Во втором будем искать НОК. Заметим, что 6 = 2 · 3; 9 = 3 · 3. Последние множители в этих разложениях равны, а первые взаимно просты. Следовательно, НОК(6; 9) = 2 · 3 · 3 = 18.

Что делать, если у дроби есть целая часть

Могу вас обрадовать: разные знаменатели у дробей — это еще не самое большое зло. Гораздо больше ошибок возникает тогда, когда в дробях-слагаемых выделена целая часть.

Безусловно, для таких дробей существуют собственные алгоритмы сложения и вычитания, но они довольно сложны и требуют долгого изучения. Лучше используйте простую схему, приведенную ниже:

1. Перевести все дроби, содержащие целую часть, в неправильные. Получим нормальные слагаемые (пусть даже с разными знаменателями), которые считаются по правилам, рассмотренным выше;
2. Собственно, вычислить сумму или разность полученных дробей. В результате мы практически найдем ответ;
3. Если это все, что требовалось в задаче, выполняем обратное преобразование, т.е. избавляемся от неправильной дроби, выделяя в ней целую часть.

Правила перехода к неправильным дробям и выделения целой части подробно описаны в уроке «Что такое числовая дробь ». Если не помните — обязательно повторите. Примеры:

Задача. Найдите значение выражения:

Здесь все просто. Знаменатели внутри каждого выражения равны, поэтому остается перевести все дроби в неправильные и сосчитать. Имеем:

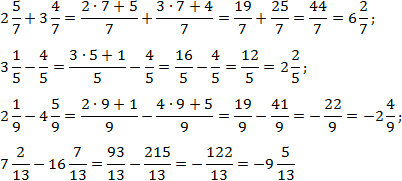
Чтобы упростить выкладки, я пропустил некоторые очевидные шаги в последних примерах.

Небольшое замечание к двум последним примерам, где вычитаются дроби с выделенной целой частью. Минус перед второй дробью означает, что вычитается именно вся дробь, а не только ее целая часть.

Перечитайте это предложение еще раз, взгляните на примеры — и задумайтесь. Именно здесь начинающие допускают огромное количество ошибок. Такие задачи обожают давать на контрольных работах. Вы также неоднократно встретитесь с ними в тестах к этому уроку, которые будут опубликованы в ближайшее время.

Резюме: общая схема вычислений

В заключение приведу общий алгоритм, который поможет найти сумму или разность двух и более дробей:

1. Если в одной или нескольких дробях выделена целая часть, переведите эти дроби в неправильные;
2. Приведите все дроби к общему знаменателю любым удобным для вас способом (если, конечно, этого не сделали составители задач);
3. Сложите или вычтите полученные числа по правилам сложения и вычитания дробей с одинаковыми знаменателями;
4. Если возможно, сократите полученный результат. Если дробь оказалась неправильной, выделите целую часть.

Помните, что выделять целую часть лучше в самом конце задачи, непосредственно перед записью ответа.

СЛОЖЕНИЕ И ВЫЧИТАНИЕ

чисел с разными знаками

Добиться того, чтобы ученик за меньшее, чем прежде, время овладел большим объемом знаний, основательных и действенных — такова одна из главных задач современной педагогики. В этой связи появляется необходимость начинать изучение нового через повторение старого, уже изученного, известного по данной теме материала. Чтобы повторение проходило быстро и для того, чтобы была наиболее наглядной связь нового со старым, надо при объяснении организовать запись изучаемого материала специальным образом.

В качестве примера расскажу о том, как я обучаю учеников сложению и вычитанию чисел с разными знаками с помощью координатной прямой. Перед изучением темы непосредственно и на протяжении уроков в 5-м и 6-м классах уделяю много внимания устройству координатной прямой. До начала изучения темы «Сложение и вычитание чисел с разными знаками» необходимо, чтобы каждый ученик твердо знал и умел ответить на следующие вопросы:

1) Как устроена координатная прямая?

2) Как располагаются на ней числа?

3) Чему равно расстояние от числа 0 до любого числа?

Учащиеся должны понимать, что движение вдоль прямой вправо приводит к увеличению числа, т.е. выполняется действие сложения, а влево — к его уменьшению, т.е. выполняется действие вычитания чисел. Чтобы работа с координатной прямой не вызывала скуки, существует много игровых нестандартных задач. Например, такая.

Вдоль шоссе начерчена прямая. Длина одного единичного отрезка равна 2 м. все двигаются только вдоль прямой. На числе 3 стоят Гена и Чебурашка. Они одновременно пошли в разные стороны и одновременно остановились. Гена прошел в 2 раза большее расстояние, чем Чебурашка, и оказался на числе 11. На каком числе оказался Чебурашка? Сколько Чебурашка прошел метров? Кто из них шел медленнее и во сколько раз?(Нестандартная математика в школе. — М., Лайда, 1993, № 62).

Когда я твердо уверена, что все ученики справляются с движениями вдоль прямой, а это очень важно, перехожу непосредственно к обучению сложению и вычитанию чисел одновременно.

Каждому учащемуся выдается опорный конспект. Разбирая положения конспекта и опираясь на уже имеющиеся геометрические наглядные картинки координатной прямой, учащиеся получают новые знания. (Конспект приведен на рисунке). Изучение темы начинается с записи в тетради вопросов, которые будут рассмотрены.

1. Как выполнить сложение с помощью координатной прямой? Как найти неизвестное слагаемое? Рассматриваем соответствующую часть конспекта??. Вспоминаем, что к aприбавить b— это значит увеличить aна bи движение вдоль координатной прямой происходит вправо. Вспоминаем, как называются и вычисляются компоненты при сложении и законы сложения, а также свойства нуля при сложении. Это части?? и?? конспекта. Поэтому следующие вопросы, записанные в тетради, таковы:

1). Сложение — это движение вправо.

СЛ. + СЛ. = С; СЛ. = С — СЛ.

2). Законы сложения:

1) переместительный закон: a+b=b+a;

2) сочетательный закон: (a+b) +c=a+ (b+c) = (a+c) +b

3). Свойства нуля при сложении: a+0=a;0+a=a;a+ (-a) =0.

4). Вычитание — это движение влево.

У. — В. = Р.; У. = В. + Р.; В. = У. — Р.

5). Сложение можно заменить вычитанием, а вычитание — сложением.

4 + 3 = — 1 3 — 4 = -1

4 + 3 = 3 + (- 4) = 3 — 4 = — 1

по переместительному закону сложения

6). Так раскрывают скобки:

+ (a+b+c) = +a+b+c

«джентельмен»

— (a + b + c) = — a — b — c

«разбойник»

2. Законы сложения.

3. Перечислите свойства нуля при сложении.

4. Как выполнить с помощью координатной прямой вычитание чисел? Правила нахождения неизвестных вычитаемого, уменьшаемого.

5. Как выполняется переход от сложения к вычитанию и от вычитания к сложению?

6. Как раскрыть скобки, перед которыми стоит: а) знак плюс; б) знак минус?

Теоретический материал довольно объемен, но так как каждая его часть связана и как бы «вытекает» одна из другой, запоминание происходит успешно. Работа с конспектом на этом не заканчивается. С каждой частью конспекта соотносится текст учебника, который прочитывается в классе. Если после этого ученик считает, что разбираемая часть ему полностью понятна, то он слегка закрашивает текст конспекта в соответствующую рамочку, как бы говоря: «Это я понял». Если же есть что-то непонятное, то рамочка не закрашивается до тех пор, пока не станет все ясно. Белая часть конспекта — сигнал «Разберись!»

Цель учителя, которую следует достичь к концу урока, такова: учащиеся, уходя с урока, должны помнить, что сложение — это движение вдоль координатной прямой вправо, а вычитание — влево. Все ученики научились раскрывать скобки. Раскрытию скобок уделяется все оставшееся время урока. Устно и письменно раскрываем скобки в заданиях типа:

); — 20 + (- 7 + (- 5)).

Задание на дом.Ответьте на записанные в тетради вопросы, читая пункты учебника, указанные в конспекте.

На следующем уроке отрабатываем алгоритм сложения и вычитания чисел. У каждого учащегося на столе карта с инструкциями:

1) Спишите пример.

2) Раскройте, если они есть, скобки.

3) Нарисуйте координатную прямую.

4) Отметьте на ней без масштаба первое число.

5) Если за числом стоит знак «+», то двигайтесь вправо, а если знак «-» — то влево на столько единичных отрезков, сколько их содержит второе слагаемое. Нарисуйте это схематически и около числа, которое ищете, поставьте знак?

6) Поставьте вопрос «Где нуль?».

7) Определите знак числа, у которого стоит вопросительный знак, являющегося решением, так: если? стоит справа от 0, то у ответа знак +, а если? стоит слева от 0, то у ответа знак — . Запишите в ответе примера после знака = найденный знак.

8) Отметьте на чертеже три отрезка.

9) Найдите длину отрезка от нуля до знака?

Пример 1.— 35 + (- 9) = — 35 — 9 = — 44.

1. Списываю пример и раскрываю скобки.

2. Рисую картинку и рассуждаю так:

а) отмечаю — 35 и двигаюсь влево на 9 единичных отрезков; у искомого числа ставлю знак?;

б) спрашиваю себя: «Где нуль?». Отвечаю: «Нуль правее — 35 на 35 единичных отрезков, значит, знак у ответа -, так как? левее нуля»;

в) ищу расстояние от 0 до знака?. Для этого вычисляю 35 + 9 = 44 и приписываю полученное число в ответ к знаку — .

Пример 2.— 35 + 9.

Пример 3.9 — 35.

Эти примеры решаем, проводя аналогичные примеру 1 рассуждения. Других случаев расположения чисел быть не может, и каждая картинка соответствует одному из правил, приведенных в учебнике и требующих запоминания. Проверено (и неоднократно), что данный способ сложения более рационален. Кроме того, он позволяет складывать числа даже тогда, когда ученик думает, что он ни одного правила не помнит. Данный способ работает и при действиях с дробями, нужно лишь привести их к общему знаменателю, а затем рисовать картинку. Например,

«Инструктивной» карточкой каждый пользуется до тех пор, пока в ней есть необходимость.

Такая работа заменяет нудное и однообразное действие счета по правилам живой и активно работающей мысли. Преимуществ множество: не надо зубрить и лихорадочно соображать, какое правило применять; легко запоминается устройство координатной прямой, а это и в алгебре, и в геометрии при вычислении величины отрезка, когда точка на прямой лежит между двумя другими точками. Эта методика эффективна как в классах с углубленным изучением математики, так и в классах возрастной нормы и даже в классах коррекции.