Линейная зависимость системы векторов. Коллинеарные векторы

Система векторов , называется линейно зависимой , если существуют такие числа , среди которых хотя бы одно отлично от нуля, что выполняется равенство https://pandia.ru/text/78/624/images/image004_77.gif" width="57" height="24 src=">.

Если же это равенство выполняется только в том случае, когда все , то система векторов называется линейно независимой .

Теорема. Система векторов , будет линейно зависимой тогда и только тогда, когда хотя бы один из ее векторов является линейной комбинацией остальных.

Пример 1. Многочлен является линейной комбинацией многочленов https://pandia.ru/text/78/624/images/image010_46.gif" width="88 height=24" height="24">. Многочлены составляют линейно независимую систему, так как многочлен https://pandia.ru/text/78/624/images/image012_44.gif" width="129" height="24">.

Пример 2. Система матриц , , https://pandia.ru/text/78/624/images/image016_37.gif" width="51" height="48 src="> является линейно независимой, так как линейная комбинация равна нулевой матрице только в том случае, когда https://pandia.ru/text/78/624/images/image019_27.gif" width="69" height="21">, , https://pandia.ru/text/78/624/images/image022_26.gif" width="40" height="21"> линейно зависимой.

Решение.

Составим линейную комбинацию данных векторов https://pandia.ru/text/78/624/images/image023_29.gif" width="97" height="24">=0..gif" width="360" height="22">.

Приравнивая одноименные координаты равных векторов, получаем https://pandia.ru/text/78/624/images/image027_24.gif" width="289" height="69">

Окончательно получим

и

Система имеет единственное тривиальное решение, поэтому линейная комбинация данных векторов равна нулю только в случае, когда все коэффициенты равны нулю. Поэтому данная система векторов линейно независима.

Пример 4. Векторы линейно независимы. Какими будут системы векторов

a). ;

b). ?

Решение.

a). Составим линейную комбинацию и приравняем её к нулю

Используя свойства операций с векторами в линейном пространстве, перепишем последнее равенство в виде

Так как векторы линейно независимы, то коэффициенты при должны быть равны нулю, т. е..gif" width="12" height="23 src=">

Полученная система уравнений имеет единственное тривиальное решение .

Так как равенство (*) выполняется только при https://pandia.ru/text/78/624/images/image031_26.gif" width="115 height=20" height="20"> – линейно независимы;

b). Составим равенство https://pandia.ru/text/78/624/images/image039_17.gif" width="265" height="24 src=">(**)

Применяя аналогичные рассуждения, получим

Решая систему уравнений методом Гаусса, получим

или

Последняя система имеет бесконечное множество решений https://pandia.ru/text/78/624/images/image044_14.gif" width="149" height="24 src=">. Таким образом, существует, ненулевой набор коэффициентов, для которого выполняется равенство (**) . Следовательно, система векторов – линейно зависима.

Пример 5 Система векторов линейно независима, а система векторов линейно зависима..gif" width="80" height="24">.gif" width="149 height=24" height="24">(***)

В равенстве (***) . Действительно, при система была бы линейно зависимой.

Из соотношения (***) получаем или Обозначим .

Получим

Задачи для самостоятельного решения (в аудитории)

1. Система, содержащая нулевой вектор, линейно зависима.

2. Система, состоящая из одного вектора а , линейно зависима тогда и только тогда, когда, а=0 .

3. Система, состоящая из двух векторов, линейно зависима тогда и только тогда, когда, векторы пропорциональны (т. е. один из них получается из другого умножением на число).

4. Если к линейно зависимой системе добавить вектор, то получится линейно зависимая система.

5. Если из линейно независимой системы удалить вектор, то полученная система векторов линейна независима.

6. Если система S линейно независима, но становится линейно зависимой при добавлении вектора b , то вектор b линейно выражается через векторы системы S .

c). Система матриц , , в пространстве матриц второго порядка.

10. Пусть система векторов a, b, c векторного пространства линейно независима. Докажите линейную независимость следующих систем векторов:

a). a+ b, b, c.

b). a+ https://pandia.ru/text/78/624/images/image062_13.gif" width="15" height="19">– произвольное число

c). a+ b, a+c, b+c.

11. Пусть a, b, c – три вектора на плоскости, из которых можно сложить треугольник. Будут ли эти векторы линейно зависимы?

12. Даны два вектора a1=(1, 2, 3, 4), a2=(0, 0, 0, 1) . Подобрать ещё два четырёхмерных вектора a3 и a4 так, чтобы система a1, a2, a3, a4 была линейно независимой.

Векторы, их свойства и действия с ними

Векторы, действия с векторами, линейное векторное пространство.

Векторы- упорядоченная совокупность конечного количества действительных чисел.

Действия: 1.Умножение вектора на число: лямда*вектор х=(лямда*х 1 , лямда*х 2 … лямда*х n).(3,4, 0, 7)*3=(9, 12,0,21)

2.Сложение векторов (принадлежат одному и тому же векторному пространству) вектор х+вектор у = (х 1 +у 1, х 2 +у 2, … х n +у n ,)

3. Вектор 0=(0,0…0)---n E n – n-мерное (линейное пространство) вектор х +вектор 0 = вектор х

Теорема. Для того чтобы система n векторов, n- мерного линейного пространства была линейно зависимой, необходимо и достаточно, чтобы один из векторов были линейной комбинацией остальным.

Теорема. Любая совокупность n+ 1ого вектора n- мерного линейного пространства явл. линейно зависимой.

Сложение векторов, умножение векторов на числа. Вычитание векторов.

Суммой двух векторов и называется вектор, направленный из начала вектора в конец вектора при условии, что начало совпадет с концом вектора. Если векторы заданы их разложениями по базисным ортам, то при сложении векторов складываются их соответствующие координаты.

Рассмотрим это на примере декартовой системы координат. Пусть

Покажем, что

Из рисунка 3 видно, что

Сумма любого конечного числа векторов может быть найдена по правилу многоугольника (рис. 4): чтобы построить сумму конечного числа векторов, достаточно совместить начало каждого последующего вектора с концом предыдущего и построить вектор, соединяющий начало первого вектора с концом последнего.

Свойства операции сложения векторов:

В этих выражениях m, n - числа.

Разностью векторов и называют вектор Второе слагаемое является вектором, противоположным вектору по направлению, но равным ему по длине.

Таким образом, операция вычитания векторов заменяется на операцию сложения

Вектор, начало которого находится в начале координат, а конец - в точке А (x1, y1, z1), называют радиус-вектором точки А и обозначают или просто. Так как его координаты совпадают с координатами точки А, то его разложение по ортам имеет вид

Вектор, имеющий начало в точке А(x1, y1, z1) и конец в точке B(x2, y2, z2), может быть записан в виде

где r 2 - радиус-вектор точки В; r 1 - радиус-вектор точки А.

Поэтому разложение вектора по ортам имеет вид

Его длина равна расстоянию между точками А и В

УМНОЖЕНИЕ

Так в случае плоской задачи произведение вектор на a = {ax; ay} на число b находится по формуле

a · b = {ax · b; ay · b}

Пример 1. Найти произведение вектора a = {1; 2} на 3.

3 · a = {3 · 1; 3 · 2} = {3; 6}

Так в случае пространственной задачи произведение вектора a = {ax; ay; az} на число b находится по формуле

a · b = {ax · b; ay · b; az · b}

Пример 1. Найти произведение вектора a = {1; 2; -5} на 2.

2 · a = {2 · 1; 2 · 2; 2 · (-5)} = {2; 4; -10}

Скалярное произведение векторов и где - угол между векторами и ; если либо , то

Из определения скалярного произведения следует, что

где, например, есть величина проекции вектора на направление вектора .

Скалярный квадрат вектора:

Свойства скалярного произведения:

Скалярное произведение в координатах

Если то

Угол между векторами

Угол между векторами - угол между направлениями этих векторов (наименьший угол).

Векторное произведение(Векторное произведение двух векторов.)- это псевдовектор, перпендикулярный плоскости, построенной по двум сомножителям, являющийся результатом бинарной операции «векторное умножение» над векторами в трёхмерном Евклидовом пространстве. Произведение не является ни коммутативным, ни ассоциативным (оно является антикоммутативным) и отличается от скалярного произведения векторов. Во многих задачах инженерии и физики нужно иметь возможность строить вектор, перпендикулярный двум имеющимся - векторное произведение предоставляет эту возможность. Векторное произведение полезно для «измерения» перпендикулярности векторов - длина векторного произведения двух векторов равна произведению их длин, если они перпендикулярны, и уменьшается до нуля, если векторы параллельны либо антипараллельны.

Векторное произведение определено только в трёхмерном и семимерном пространствах. Результат векторного произведения, как и скалярного, зависит от метрики Евклидова пространства.

В отличие от формулы для вычисления по координатам векторов скалярного произведения в трёхмерной прямоугольной системе координат, формула для векторного произведения зависит от ориентации прямоугольной системы координат или, иначе, её «хиральности»

Коллинеарность векторов.

Два ненулевых (не равных 0) вектора называются коллинеа́рными, если они лежат на параллельных прямых или на одной прямой. Допусти́м, но не рекомендуется синоним - «параллельные» векторы. Коллинеарные векторы могут быть одинаково направлены («сонаправлены») или противоположно направлены (в последнем случае их иногда называют «антиколлинеарными» или «антипараллельными»).

Сме́шанное произведе́ние векторов(a, b,c) - скалярное произведение вектора a на векторное произведение векторов b и c:

(a,b,c)=a ⋅(b ×c)

иногда его называют тройным скалярным произведением векторов, по всей видимости из-за того, что результатом является скаляр (точнее - псевдоскаляр).

Геометрический смысл: Модуль смешанного произведения численно равен объёму параллелепипеда, образованного векторами(a,b,c) .

Свойства

Смешанное произведение кососимметрично по отношению ко всем своим аргументам:т. е. перестановка любых двух сомножителей меняет знак произведения. Отсюда следует, чтоСмешанное произведение в правой декартовой системе координат (в ортонормированном базисе) равно определителю матрицы, составленной из векторов и:

Смешанное произведение в левой декартовой системе координат (в ортонормированном базисе) равно определителю матрицы, составленной из векторов и, взятому со знаком "минус":

В частности,

Если любые два вектора параллельны, то с любым третьим вектором они образуют смешанное произведение равное нулю.

Если три вектора линейно зависимы (т. е. компланарны, лежат в одной плоскости), то их смешанное произведение равно нулю.

Геометрический смысл - Смешанное произведение по абсолютному значению равно объёму параллелепипеда (см. рисунок), образованного векторами и; знак зависит от того, является ли эта тройка векторов правой или левой.

Компланарность векторов.

Три вектора (или большее число) называются компланарными, если они, будучи приведенными к общему началу, лежат в одной плоскости

Свойства компланарности

Если хотя бы один из трёх векторов - нулевой, то три вектора тоже считаются компланарными.

Тройка векторов, содержащая пару коллинеарных векторов, компланарна.

Смешанное произведение компланарных векторов. Это - критерий компланарности трёх векторов.

Компланарные векторы - линейно зависимы. Это - тоже критерий компланарности.

В 3-мерном пространстве 3 некомпланарных вектора образуют базис

Линейно зависимые и линейно независимые векторы.

Линейно зависимые и независимые системы векторов. Определение . Система векторов называется линейно зависимой , если существует хотя бы одна нетривиальная линейная комбинация этих векторов, равная нулевому вектору. В противном случае, т.е. если только тривиальная линейная комбинация данных векторов равна нулевому вектору, векторы называются линейно независимыми .

Теорема (критерий линейной зависимости) . Для того чтобы система век торов линейного пространства была линейно зависимой, необходимо и достаточно, чтобы, по крайней мере, один из этих векторов являлся линейной комбинацией остальных.

1) Если среди векторов имеется хотя бы один нулевой вектор, то вся система векторов линейно зависима.

В самом деле, если, например, , то, полагая , имеем нетривиальную линейную комбинацию .▲

2) Если среди векторов некоторые образуют линейно зависимую систему, то и вся система линейно зависима.

Действительно, пусть векторы , , линейно зависимы. Значит, существует нетривиальная линейная комбинация , равная нулевому вектору. Но тогда, полагая , получим также нетривиальную линейную комбинацию , равную нулевому вектору.

2. Базис и размерность. Определение . Система линейно независимых векторов векторного пространства называетсябазисом этого пространства, если любой вектор из может быть представлен в виде линейной комбинации векторов этой системы, т.е. для каждого вектора существуют вещественные числа такие, что имеет место равенство Это равенство называется разложением вектора по базису , а числа называютсякоординатами вектора относительно базиса (или в базисе ) .

Теорема (о единственности разложения по базису) . Каждый вектор пространства может быть разложен по базису единственным образом, т.е. координаты каждого вектора в базисе определяются однозначно.

Чтобы проверить является ли система векторов линейно-зависимой, необходимо составить линейную комбинацию этих векторов , и проверить, может ли она быть рана нулю, если хот один коэффициент равен нулю.

Случай 1. Система векторов заданна векторами

Составляем линейную комбинацию

Мы получили однородную систему уравнений. Если она имеет ненулевое решение, то определитель должен быть равен нулю. Составим определитель и найдём его значение.

Определитель равен нулю, следовательно, вектора линейно зависимы.

Случай 2. Система векторов заданна аналитическими функциями:

a)
, если тождество верно, значит система линейно зависима.

Составим линейную комбинацию.

Необходимо проверить, существуют ли такие a, b, c (хотя бы одна из которых не равна нулю) при которых данное выражение равно нулю.

Запишем гиперболические функции

,
, тогда

тогда линейная комбинация векторов примет вид:

Откуда
, возьмём, например,, тогда линейная комбинацияравна нулю, следовательно, система линейно зависима.

Ответ: система линейно зависима.

b)
, составим линейную комбинацию

Линейная комбинация векторов, должна быть равна нулю для любых значений x.

Проверим для частных случаев.

Линейная комбинация векторов равна нулю, только если все коэффициенты равны нулю.

Следовательно, система линейно не зависима.

Ответ: система линейно не зависима.

5.3. Найти какой-нибудь базис и определить размерность линейного пространства решений.

Сформируем расширенную матрицу и приведём её к виду трапеции методом Гаусса.

Чтоб получить какой-нибудь базис подставим произвольные значения:

Получим остальные координаты

Ответ:

5.4. Найти координаты вектора X в базисе, если он задан в базисе.

Нахождение координат вектора в новом базисе сводится к решению системы уравнений

Способ 1. Нахождение при помощи матрицы перехода

Составим матрицу перехода

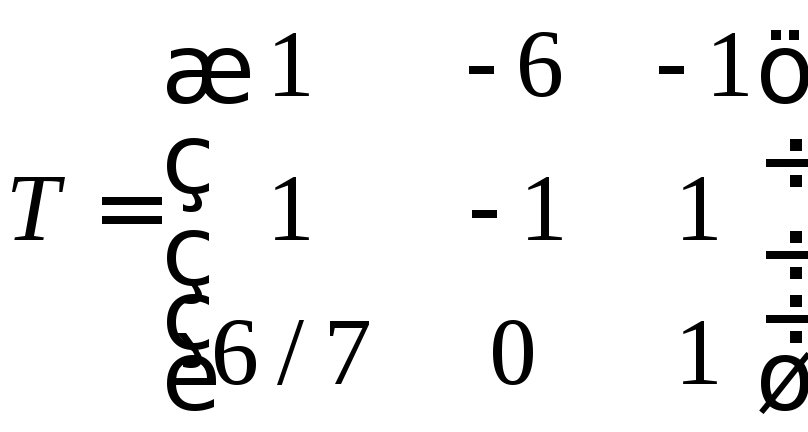
Найдём вектор в новом базисе по формуле

Найдём обратную матрицу и выполним умножение

,

Способ 2. Нахождение путем составления системы уравнений.

Составим базисные вектора из коэффициентов базиса

,
,

Нахождение вектора в новом базисе имеет вид

, где d это заданный вектор x .

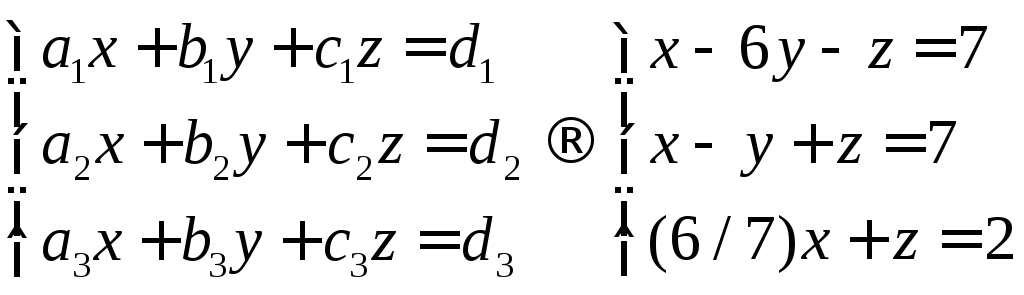
Полученное уравнение можно решить любым способом, ответ будет аналогичным.

Ответ: вектор в новом базисе
.

5.5. Пусть x = ( x 1 , x 2 , x 3 ) . Являются ли линейными следующие преобразования.

Составим матрицы линейных операторов из коэффициентов заданных векторов.

Проверим свойство линейных операций для каждой матрицы линейного оператора.

Левую часть найдём умножением матрицы А на вектор

Правую часть найдем, умножив заданный вектор на скаляр
.

Мы видим, что
значит, преобразование не является линейным.

Проверим другие вектора.

, преобразование не является линейным.

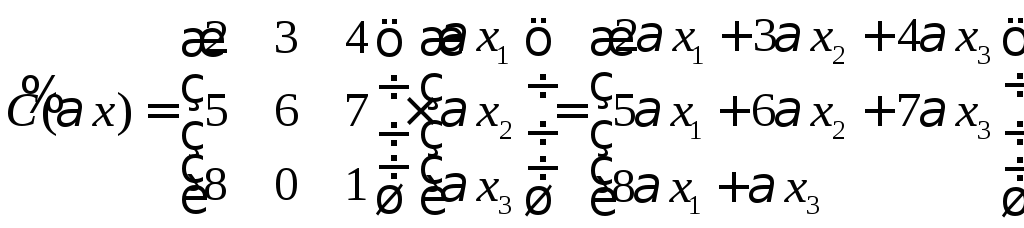
, преобразование является линейным.

Ответ: Ах – не линейное преобразование, Вх – не линейное, Сх – линейное.

Примечание. Можно выполнить данное задание гораздо проще, внимательно посмотрев на заданные вектора. В Ах мы видим, что есть слагаемые которые не содержат элементы х , что не могло быть получено в результате линейной операции. В Вх есть элемент х в третьей степени, что также не могло быть получено умножением на вектор х .

5.6. Дано x = { x 1 , x 2 , x 3 } , Ax = { x 2 – x 3 , x 1 , x 1 + x 3 } , Bx = { x 2 , 2 x 3 , x 1 } . Выполнить заданную операцию: ( A ( B – A )) x .

Выпишем матрицы линейных операторов.

Выполним операцию над матрицами

При умножении полученной матрицы на Х, получим

Ответ:

В данной статье мы расскажем:

• что такое коллинеарные векторы;
• какие существуют условия коллинеарности векторов;
• какие существуют свойства коллинеарных векторов;
• что такое линейная зависимость коллинеарных векторов.

Yandex.RTB R-A-339285-1 Определение 1

Коллинеарные векторы - это векторы, которые являются параллелями одной прямой или лежат на одной прямой.

Пример 1

Условия коллинеарности векторов

Два векторы являются коллинеарными, если выполняется любое из следующих условий:

• условие 1 . Векторы a и b коллинеарны при наличии такого числа λ , что a = λ b ;
• условие 2 . Векторы a и b коллинеарны при равном отношении координат:

a = (a 1 ; a 2) , b = (b 1 ; b 2) ⇒ a ∥ b ⇔ a 1 b 1 = a 2 b 2

• условие 3 . Векторы a и b коллинеарны при условии равенства векторного произведения и нулевого вектора:

a ∥ b ⇔ a , b = 0

Замечание 1

Условие 2 неприменимо, если одна из координат вектора равна нулю.

Замечание 2

Условие 3 применимо только к тем векторам, которые заданы в пространстве.

Примеры задач на исследование коллинеарности векторов

Пример 1

Исследуем векторы а = (1 ; 3) и b = (2 ; 1) на коллинеарность.

Как решить?

В данном случае необходимо воспользоваться 2-м условием коллинеарности. Для заданных векторов оно выглядит так:

Равенство неверное. Отсюда можно сделать вывод, что векторы a и b неколлинеарны.

Ответ : a | | b

Пример 2

Какое значение m вектора a = (1 ; 2) и b = (- 1 ; m) необходимо для коллинеарности векторов?

Как решить?

Используя второе условие коллинераности, векторы будут коллинеарными, если их координаты будут пропорциональными:

Отсюда видно, что m = - 2 .

Ответ: m = - 2 .

Критерии линейной зависимости и линейной независимости систем векторов

Теорема

Система векторов векторного пространства линейно зависима только в том случае, когда один из векторов системы можно выразить через остальные векторы данной системы.

Доказательство

Пусть система e 1 , e 2 , . . . , e n является линейно зависимой. Запишем линейную комбинацию этой системы равную нулевому вектору:

a 1 e 1 + a 2 e 2 + . . . + a n e n = 0

в которой хотя бы один из коэффициентов комбинации не равен нулю.

Пусть a k ≠ 0 k ∈ 1 , 2 , . . . , n .

Делим обе части равенства на ненулевой коэффициент:

a k - 1 (a k - 1 a 1) e 1 + (a k - 1 a k) e k + . . . + (a k - 1 a n) e n = 0

Обозначим:

A k - 1 a m , где m ∈ 1 , 2 , . . . , k - 1 , k + 1 , n

В таком случае:

β 1 e 1 + . . . + β k - 1 e k - 1 + β k + 1 e k + 1 + . . . + β n e n = 0

или e k = (- β 1) e 1 + . . . + (- β k - 1) e k - 1 + (- β k + 1) e k + 1 + . . . + (- β n) e n

Отсюда следует, что один из векторов системы выражается через все остальные векторы системы. Что и требовалось доказать (ч.т.д.).

Достаточность

Пусть один из векторов можно линейно выразить через все остальные векторы системы:

e k = γ 1 e 1 + . . . + γ k - 1 e k - 1 + γ k + 1 e k + 1 + . . . + γ n e n

Переносим вектор e k в правую часть этого равенства:

0 = γ 1 e 1 + . . . + γ k - 1 e k - 1 - e k + γ k + 1 e k + 1 + . . . + γ n e n

Поскольку коэффициент вектора e k равен - 1 ≠ 0 , у нас получается нетривиальное представление нуля системой векторов e 1 , e 2 , . . . , e n , а это, в свою очередь, означает, что данная система векторов линейно зависима. Что и требовалось доказать (ч.т.д.).

Следствие:

• Система векторов является линейно независимой, когда ни один из ее векторов нельзя выразить через все остальные векторы системы.
• Система векторов, которая содержит нулевой вектор или два равных вектора, линейно зависима.

Свойства линейно зависимых векторов

1. Для 2-х и 3-х мерных векторов выполняется условие: два линейно зависимых вектора - коллинеарны. Два коллинеарных вектора - линейно зависимы.
2. Для 3-х мерных векторов выполняется условие: три линейно зависимые вектора - компланарны. (3 компланарных вектора - линейно зависимы).
3. Для n-мерных векторов выполняется условие: n + 1 вектор всегда линейно зависимы.

Примеры решения задач на линейную зависимость или линейную независимость векторов

Пример 3

Проверим векторы a = 3 , 4 , 5 , b = - 3 , 0 , 5 , c = 4 , 4 , 4 , d = 3 , 4 , 0 на линейную независимость.

Решение. Векторы являются линейно зависимыми, поскольку размерность векторов меньше количества векторов.

Пример 4

Проверим векторы a = 1 , 1 , 1 , b = 1 , 2 , 0 , c = 0 , - 1 , 1 на линейную независимость.

Решение. Находим значения коэффициентов, при которых линейная комбинация будет равняться нулевому вектору:

x 1 a + x 2 b + x 3 c 1 = 0

Записываем векторное уравнение в виде линейного:

x 1 + x 2 = 0 x 1 + 2 x 2 - x 3 = 0 x 1 + x 3 = 0

Решаем эту систему при помощи метода Гаусса:

1 1 0 | 0 1 2 - 1 | 0 1 0 1 | 0 ~

Из 2-ой строки вычитаем 1-ю, из 3-ей - 1-ю:

~ 1 1 0 | 0 1 - 1 2 - 1 - 1 - 0 | 0 - 0 1 - 1 0 - 1 1 - 0 | 0 - 0 ~ 1 1 0 | 0 0 1 - 1 | 0 0 - 1 1 | 0 ~

Из 1-й строки вычитаем 2-ю, к 3-ей прибавляем 2-ю:

~ 1 - 0 1 - 1 0 - (- 1) | 0 - 0 0 1 - 1 | 0 0 + 0 - 1 + 1 1 + (- 1) | 0 + 0 ~ 0 1 0 | 1 0 1 - 1 | 0 0 0 0 | 0

Из решения следует, что у системы множество решений. Это значит, что существует ненулевая комбинация значения таких чисел x 1 , x 2 , x 3 , при которых линейная комбинация a , b , c равняется нулевому вектору. Следовательно, векторы a , b , c являются линейно зависимыми.

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

a 1 = { 3, 5, 1 , 4 }, a 2 = { –2, 1, -5 , -7 }, a 3 = { -1, –2, 0, –1 }.

Р е ш е н и е. Ищем общее решение системы уравнений

a 1 x 1 + a 2 x 2 + a 3 x 3 = Θ

методом Гаусса. Для этого запишем эту однородную систему по координатам:

Матрица системы

Разрешенная система имеет вид: (r A = 2, n = 3). Система совместна и неопределена. Ее общее решение (x 2 – свободная переменная): x 3 = 13x 2 ; 3x 1 – 2x 2 – 13x 2 = 0 => x 1 = 5x 2 => X o = . Наличие ненулевого частного решения, например, , говорит о том, векторы a 1 , a 2 , a 3 линейно зависимы.

Пример 2.

Выяснить, является ли данная система векторов линейно зависимой или линейно независимой:

1. a 1 = { -20, -15, - 4 }, a 2 = { –7, -2, -4 }, a 3 = { 3, –1, –2 }.

Р е ш е н и е. Рассмотрим однородную систему уравнений a 1 x 1 + a 2 x 2 + a 3 x 3 = Θ

или в развернутом виде (по координатам)

Система однородна. Если она невырождена, то она имеет единственное решение. В случае однородной системы – нулевое (тривиальное) решение. Значит, в этом случае система векторов независима. Если же система вырождена, то она имеет ненулевые решения и, следовательно, она зависима.

Проверяем систему на вырожденность:

= –80 – 28 + 180 – 48 + 80 – 210 = – 106 ≠ 0.

Система невырождена и, т.о., векторы a 1 , a 2 , a 3 линейно независимы.

Задания. Выяснить, является ли данная система векторов линейно зависимой или линейно независимой:

1. a 1 = { -4, 2, 8 }, a 2 = { 14, -7, -28 }.

2. a 1 = { 2, -1, 3, 5 }, a 2 = { 6, -3, 3, 15 }.

3. a 1 = { -7, 5, 19 }, a 2 = { -5, 7 , -7 }, a 3 = { -8, 7, 14 }.

4. a 1 = { 1, 2, -2 }, a 2 = { 0, -1, 4 }, a 3 = { 2, -3, 3 }.

5. a 1 = { 1, 8 , -1 }, a 2 = { -2, 3, 3 }, a 3 = { 4, -11, 9 }.

6. a 1 = { 1, 2 , 3 }, a 2 = { 2, -1 , 1 }, a 3 = { 1, 3, 4 }.

7. a 1 = {0, 1, 1 , 0}, a 2 = {1, 1 , 3, 1}, a 3 = {1, 3, 5, 1}, a 4 = {0, 1, 1, -2}.

8. a 1 = {-1, 7, 1 , -2}, a 2 = {2, 3 , 2, 1}, a 3 = {4, 4, 4, -3}, a 4 = {1, 6, -11, 1}.

9. Доказать, что система векторов будет линейно зависимой, если она содержит:

а) два равных вектора;

б) два пропорциональных вектора.