Логарифмические неравенства и их решения. Логарифмические неравенства. Исчерпывающий гид (2019)
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо - в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ - раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности - включая административные, технические и физические - для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
Среди всего многообразия логарифмических неравенств отдельно изучают неравенства с переменным основанием. Они решаются по специальной формуле, которую почему-то редко рассказывают в школе:
log k (x ) f (x ) ∨ log k (x ) g (x ) ⇒ (f (x ) − g (x )) · (k (x ) − 1) ∨ 0
Вместо галки «∨» можно поставить любой знак неравенства: больше или меньше. Главное, чтобы в обоих неравенствах знаки были одинаковыми.
Так мы избавляемся от логарифмов и сводим задачу к рациональному неравенству. Последнее решается намного проще, но при отбрасывании логарифмов могут возникнуть лишние корни. Чтобы их отсечь, достаточно найти область допустимых значений. Если вы забыли ОДЗ логарифма, настоятельно рекомендую повторить - см. «Что такое логарифм ».
Все, что связано с областью допустимых значений, надо выписать и решить отдельно:
f (x ) > 0; g (x ) > 0; k (x ) > 0; k (x ) ≠ 1.
Эти четыре неравенства составляют систему и должны выполняться одновременно. Когда область допустимых значений найдена, остается пересечь ее с решением рационального неравенства - и ответ готов.
Задача. Решите неравенство:
Для начала выпишем ОДЗ логарифма:
Первые два неравенства выполняются автоматически, а последнее придется расписать. Поскольку квадрат числа равен нулю тогда и только тогда, когда само число равно нулю, имеем:
x
2 + 1 ≠ 1;
x
2 ≠ 0;
x
≠ 0.
Получается, что ОДЗ логарифма - все числа, кроме нуля: x ∈ (−∞ 0)∪(0; +∞). Теперь решаем основное неравенство:
Выполняем переход от логарифмического неравенства к рациональному. В исходном неравенстве стоит знак «меньше», значит полученное неравенство тоже должно быть со знаком «меньше». Имеем:
(10 − (x
2 + 1)) · (x
2 + 1 − 1) < 0;
(9 − x
2) · x
2 < 0;
(3 − x
) · (3 + x
) · x
2 < 0.
Нули этого выражения: x = 3; x = −3; x = 0. Причем x = 0 - корень второй кратности, значит при переходе через него знак функции не меняется. Имеем:
Получаем x ∈ (−∞ −3)∪(3; +∞). Данное множество полностью содержится в ОДЗ логарифма, значит это и есть ответ.
Преобразование логарифмических неравенств
Часто исходное неравенство отличается от приведенного выше. Это легко исправить по стандартным правилам работы с логарифмами - см. «Основные свойства логарифмов ». А именно:
- Любое число представимо в виде логарифма с заданным основанием;
- Сумму и разность логарифмов с одинаковыми основаниями можно заменить одним логарифмом.
Отдельно хочу напомнить про область допустимых значений. Поскольку в исходном неравенстве может быть несколько логарифмов, требуется найти ОДЗ каждого из них. Таким образом, общая схема решения логарифмических неравенств следующая:
- Найти ОДЗ каждого логарифма, входящего в неравенство;
- Свести неравенство к стандартному по формулам сложения и вычитания логарифмов;
- Решить полученное неравенство по схеме, приведенной выше.
Задача. Решите неравенство:
Найдем область определения (ОДЗ) первого логарифма:
Решаем методом интервалов. Находим нули числителя:
3x
− 2 = 0;
x
= 2/3.
Затем - нули знаменателя:
x
− 1 = 0;
x
= 1.
Отмечаем нули и знаки на координатной стреле:
Получаем x ∈ (−∞ 2/3)∪(1; +∞). У второго логарифма ОДЗ будет таким же. Не верите - можете проверить. Теперь преобразуем второй логарифм так, чтобы в основании стояла двойка:
Как видите, тройки в основании и перед логарифмом сократились. Получили два логарифма с одинаковым основанием. Складываем их:
log 2 (x
− 1) 2 < 2;
log 2 (x
− 1) 2 < log 2 2 2 .
Получили стандартное логарифмическое неравенство. Избавляемся от логарифмов по формуле. Поскольку в исходном неравенстве стоит знак «меньше», полученное рациональное выражение тоже должно быть меньше нуля. Имеем:
(f
(x
) − g
(x
)) · (k
(x
) − 1) < 0;
((x
− 1) 2 − 2 2)(2 − 1) < 0;
x
2 − 2x
+ 1 − 4 < 0;
x
2 − 2x
− 3 < 0;
(x
− 3)(x
+ 1) < 0;
x
∈ (−1; 3).
Получили два множества:
- ОДЗ: x ∈ (−∞ 2/3)∪(1; +∞);
- Кандидат на ответ: x ∈ (−1; 3).
Осталось пересечь эти множества - получим настоящий ответ:
Нас интересует пересечение множеств, поэтому выбираем интервалы, закрашенные на обоих стрелах. Получаем x ∈ (−1; 2/3)∪(1; 3) - все точки выколоты.
Логарифмические неравенства
На предыдущих уроках мы с вами познакомились с логарифмическими уравнениями и теперь знаем, что это такое и как их решать. А сегодняшний урок будет посвящен изучению логарифмических неравенств. Что же это за такие неравенства и в чем разница между решением логарифмического уравнения и неравенства?
Логарифмические неравенства - это неравенства, которые имеют переменную, стоящую под знаком логарифма или в его основании.
Или же, можно еще сказать, что логарифмическое неравенство – это такое неравенство, в котором его неизвестная величина, как и в логарифмическом уравнении, будет стоять под знаком логарифма.
Простейшие логарифмические неравенства имеют такой вид:
где f(x) и g(x) являются некоторыми выражениями, которые зависят от x.
Давайте это рассмотрим на таком примере: f(x)=1+2x+x2, g(x)=3x−1.
Решение логарифмических неравенств
Перед решением логарифмических неравенств, стоит отметить, что они при решении имеют сходство с показательными неравенствами, а именно:
Во-первых, при переходе от логарифмов к выражениям, стоящим под знаком логарифма, нам также необходимо сравнить основание логарифма с единицей;
Во-вторых, решая логарифмическое неравенство, используя замену переменных, нам необходимо решать неравенства относительно замены до того момента, пока мы не получим простейшее неравенство.
Но это мы с вами рассмотрели сходные моменты решения логарифмических неравенств. А сейчас обратим внимание на довольно таки существенное отличие. Нам с вами известно, что логарифмическая функция обладает ограниченной областью определения, поэтому переходя от логарифмов к выражениям, стоящим под знаком логарифма, нужно брать в расчет область допустимых значений (ОДЗ).
То есть, следует учитывать, что решая логарифмическое уравнение мы с вами, можем сначала находить корни уравнения, а потом делать проверку этого решения. А вот решить логарифмическое неравенство так не получится, поскольку переходя от логарифмов к выражениям, стоящим под знаком логарифма, необходимо будет записывать ОДЗ неравенства.
Вдобавок стоит запомнить, что теория неравенств состоит из действительных чисел, которыми являются положительные и отрицательные числа, а также и число 0.
Например, когда число «а» является положительным, то необходимо использовать такую запись: a >0. В этом случае, как сумма, так и произведение таких этих чисел также будут положительными.
Основным принципом решения неравенства является его замена на более простое неравенство, но главное, чтобы оно было равносильно данному. Дальше, также мы получили неравенство и снова его заменили на то, которое имеет более простой вид и т.д.
Решая неравенства с переменной нужно находить все его решения. Если два неравенства имеют одну переменную х, то такие неравенства равносильны, при условии, что их решения совпадают.
Выполняя задания на решение логарифмических неравенств, необходимо запомнить, что когда a > 1, то логарифмическая функция возрастает, а когда 0 < a < 1, то такая функция имеет свойство убывать. Эти свойства вам будут необходимы при решении логарифмических неравенств, поэтому вы их должны хорошо знать и помнить.
Способы решения логарифмических неравенств
Сейчас рассмотрим некоторые способы, которые имеют место при решении логарифмических неравенств. Для лучшего понимания и усвоения, попытаемся в них разобраться на конкретных примерах.
Нам с вами известно, что простейшее логарифмическое неравенство имеет такой вид:
В этом неравенстве V – является одним из таких знаков неравенства, как: <,>, ≤ или ≥.
Когда основание данного логарифма больше единицы (a>1), осуществляя переход от логарифмов к выражениям, стоящим под знаком логарифма, то в этом варианте знак неравенства сохраняется, и неравенство будет иметь такой вид:
что равносильно такой вот системе:
В случае же, когда основание логарифма больше нуля и меньше единицы (0 Это равносильно данной системе: Посмотрим еще примеры решения простейших логарифмических неравенств, приведенных на картинке ниже: Задание.
Давайте попробуем решить такое вот неравенство: Решение области допустимых значений. Теперь попробуем умножить его правую часть на: Смотрим, что у нас получится: Теперь, давайте с вами перейдем к преобразованию подлогарифмических выражений. В связи с тем, что основание логарифма 0< 1/4 <1, то от сюда следует, что знак неравенства изменится на противоположный: 3x - 8 > 16; А из этого следует, что интервал, который мы получили, целиком и полностью принадлежит ОДЗ и является решением такого неравенства. Вот какой ответ у нас получился: А теперь давайте попробуем проанализировать, что нам необходимо для успешного решения логарифмических неравенств? Во-первых, сосредоточить все свое внимание и постараться не допускать ошибок при выполнении преобразований, которые даны в этом неравенстве. Также, следует запомнить, что при решении таких неравенств нужно не допускать расширений и сужений ОДЗ неравенства, которые могут привести к потере или приобретению посторонних решений. Во-вторых, при решении логарифмических неравенств необходимо научиться мыслить логически и понимать разницу между такими понятиями, как система неравенств и совокупность неравенств, чтобы вы без проблем смогли осуществлять отбор решений неравенства, при этом руководствуясь его ОДЗ. В-третьих, для успешного решения таких неравенств каждый из вас должен отлично знать все свойства элементарных функций и четко понимать их смысл. К таким функциям относятся не только логарифмические, но и рациональные, степенные, тригонометрические и т.д., одним словом, все те, которые вы изучали на протяжении школьного обучения алгебры. Как видите, изучив тему о логарифмических неравенствах, в решении этих неравенств нет ничего сложного при условии, если вы будете внимательны и настойчивы в достижении поставленных целей. Чтобы в решении неравенств не возникало никаких проблем, нужно как можно больше тренироваться, решая различные задания и при этом запоминать основные способы решения таких неравенств и их систем. При неудачных решениях логарифмических неравенств, следует внимательно проанализировать свои ошибки, чтобы в будущем не возвращаться к ним снова. Для лучшего усвоения темы и закрепления пройденного материала, решите следующие неравенства: До сдачи ЕГЭ по математике остается все меньше времени. Обстановка накаляется, нервы у школьников, родителей, учителей и репетиторов натягиваются все сильнее. Снять нервное напряжение вам помогут ежедневные углубленные занятия по математике. Ведь ничто, как известно, так не заряжает позитивом и не помогает при сдаче экзаменов, как уверенность в своих силах и знаниях. Сегодня репетитор по математике расскажет вам о решении систем логарифмических и показательных неравенств, заданий, традиционно вызывающих трудности у многих современных старшеклассников. Для того, чтобы научиться решать задачи C3 из ЕГЭ по математике как репетитор по математике рекомендую вам обратить внимание на следующие важные моменты. 1.
Прежде чем приступить к решению систем логарифмических и показательных неравенств, необходимо научиться решать каждый из этих типов неравенств в отдельности. В частности, разобраться с тем, как находится область допустимых значений, проводятся равносильные преобразования логарифмических и показательных выражений. Некоторые связанные с этим тайны вы сможете постичь, изучив статьи « » и « ». 2.
При этом необходимо осознавать, что решение системы неравенств не всегда сводится к решению отдельно каждого неравенства и пересечению полученных промежутков. Иногда, зная решение одного неравенства системы, решение второго значительно упрощается. Как репетитор по математике, занимающийся подготовкой школьников к сдаче выпускных экзаменов в формате ЕГЭ, раскрою в этой статье парочку связанных с этим секретов. 3.
Необходимо четко уяснить для себя разницу между пересечением и объединением множеств. Это одно из важнейших математических знаний, которое опытный профессиональный репетитор старается дать своему ученику уже с первых занятий. Наглядное представление о пересечении и объединении множеств дают так называемые «круги Эйлера». Пересечением множеств
называется множество, которому принадлежат только те элементы, которые есть у каждого из этих множеств.
пересечением
Изображение пересечения множеств с помощью «кругов Эйлера» Объяснение на пальцах.
У Дианы в сумочке находится «множество», состоящее из {ручки
, карандаша
, линейки
, тетрадки
, расчески
}. У Алисы в сумочке находится «множество», состоящее из {записной книжки
, карандаша
, зеркальца
, тетрадки
, котлеты по-киевски
}. Пересечением этих двух «множеств» будет «множество», состоящее из {карандаша
, тетрадки
}, поскольку оба этих «элемента» есть и у Дианы, и у Алисы. Важно запомнить!
Если решением неравенства является промежуток а решением неравенства является промежуток то решением систем:
является промежуток то есть пересечение
исходных промежутков. Здесь и далее под
подразумевается любой из знаков
title="Rendered by QuickLaTeX.com" height="17" width="93" style="vertical-align: -4px;">а под
— ему противоположный знак.
Объединением множеств
называется множество, которое состоит из всех элементов исходных множеств.
Другими словами, если даны два множества и то их объединением
будет являться множество следующего вида: Изображение объединения множеств с помощью «кругов Эйлера» Объяснение на пальцах.
Объединением «множеств», взятых в предыдущем примере будет «множество», состоящее из {ручки
, карандаша
, линейки
, тетрадки
, расчески
, записной книжки
, зеркальца
, котлеты по-киевски
}, поскольку оно состоит из всех элементов исходных «множеств». Одно уточнение, которое может оказаться не лишним. Множество не может
содержать в себе одинаковых элементов. Важно запомнить!
Если решением неравенства является промежуток а решением неравенства является промежуток то решением совокупности:
является промежуток то есть объединение
исходных промежутков. Перейдем непосредственно к примерам. Пример 1.
Решите систему неравенств:
Решение задачи C3.
1.
Решаем сперва первое неравенств. Используя замену переходим к неравенству: 2.
Решаем теперь второе неравенство. Область его допустимых значений определяется неравенством: Title="Rendered by QuickLaTeX.com"> В области допустимых значений с учетом того, что основание логарифма title="Rendered by QuickLaTeX.com" height="18" width="52" style="vertical-align: -4px;"> переходим к равносильному неравенству: Исключая решения, не входящие в область допустимых значений, получаем промежуток 3.
Ответом к системе
неравенств будет пересечение
Полученные промежутки на числовой прямой. Решение — их пересечение Пример 2.
Решите систему неравенств:
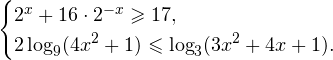
Решение задачи C3.
1.
Решаем сперва первое неравенство. Умножаем обе части на title="Rendered by QuickLaTeX.com" height="14" width="55" style="vertical-align: 0px;"> и делаем замену в результате чего приходим к неравенству: Переходим к обратной подстановке: 2.
Title="Rendered by QuickLaTeX.com"> Графическое изображение полученных промежуток. Решение системы — их пересечение Пример 3.
Решите систему неравенств:
Решение задачи C3.
1.
Решаем сперва первое неравенство. Умножаем обе его части на title="Rendered by QuickLaTeX.com" height="18" width="61" style="vertical-align: -4px;"> после чего получаем неравенство: Используя подстановку переходим к следующему неравенству: Переходим к обратной подстановке: 2.
Решаем теперь второе неравенство. Определим сначала область допустимых значений этого неравенства: ql-right-eqno">
Обращаем внимание, что Тогда с учетом области допустимых значений получаем: 3.
Находим общее решения неравенств. Сравнение полученных иррациональных значений узловых точек — задача в данном примере отнюдь не тривиальная. Сделать это можно следующим образом. Так как Title="Rendered by QuickLaTeX.com"> то Пример 4.
Решите систему неравенств:
Решение задачи С3.
1.
Решим сперва второе неравенство: 2.
Первое неравенство исходной системы представляет собой логарифмическое неравенство с переменным основанием. Удобный способ решения подобных неравенств описан в статье «Сложные логарифмические неравенства », в его основе лежит простая формула: Вместо знака может быть подставлен любой знак неравенства, главное, чтобы он был один и тот же в обоих случаях. Использование данной формулы существенно упрощает решение неравенства: Определим теперь область допустимых значений данного неравенства. Она задается следующей системой: Title="Rendered by QuickLaTeX.com"> Title="Rendered by QuickLaTeX.com"> Легко видеть, что одновременно этот промежуток будет являться и решением нашего неравенства. 3.
Окончательным ответом исходной системы
неравенств будет пересечение
полученных промежутков, то есть Пример 5.
Решите систему неравенств:
Решение задания C3.
1.
Решаем сперва первое неравенство. Используем подстановку Переходим к следующему квадратному неравенству: 2.
Решаем теперь второе неравенство. Область его допустимых значений определяется системой: Title="Rendered by QuickLaTeX.com"> Данное неравенство равносильно следующей смешанной системе: В области допустимых значений, то есть при title="Rendered by QuickLaTeX.com" height="18" width="53" style="vertical-align: -4px;"> используя равносильные преобразования переходим к следующей смешанной системе: С учетом области допустимых значений получаем: 3.
Окончательным решением исходной системы
является Решение задачи C3.
1.
Решаем сперва первое неравенство. Равносильными преобразованиями приводим его к виду: 2.
Решаем теперь второе неравенство. Область его допустимых значений определяется промежутком: title="Rendered by QuickLaTeX.com" height="14" width="68" style="vertical-align: 0px;"> Используя замену переменной переходим к следующему квадратичному неравенству: Этот ответ целиком принадлежит области допустимых значений неравенства. 3.
Пересечением полученных в предыдущих пунктах промежутков получаем окончательный ответ к системе неравенств: Сегодня мы с вами решали системы логарифмических и показательных неравенств. Задания подобного рода предлагались в пробных вариантах ЕГЭ по математике в течение всего ныне идущего учебного года. Однако, как репетитор по математике, имеющий опыт подготовки к ЕГЭ, могу сказать, что это вовсе не означает, что аналогичные задания будут в реальных вариантах ЕГЭ по математике в июне. Позволю себе высказать одно предостережение, адресованное в первую очередь репетиторам и школьным учителям, занимающимся подготовкой старшеклассников к сдаче ЕГЭ по математике. Весьма опасно готовить школьников к экзамену строго по заданным темам, ведь в этом случае возникает риск полностью «завалить» его даже при незначительном изменении ранее заявленного формата заданий. Математическое образование должно быть полным. Уважаемые коллеги, пожалуйста, не уподобляйте роботам своих учеников так называемым «натаскиванием» на решение определенного типа задач. Ведь нет ничего хуже формализации мышления человека. Всем удачи и творческих успехов! Если пробовать, то есть два варианта: получится или не получится. Если не пробовать — всего один. Вам кажется, что до ЕГЭ еще есть время, и вы успеете подготовиться? Быть может, это и так. Но в любом случае, чем раньше школьник начинает подготовку, тем успешнее он сдает экзамены. Сегодня мы решили посвятить статью логарифмическим неравенствам. Это одно из заданий, а значит, возможность получить дополнительный балл. Вы уже знаете, что такое логарифм(log)? Мы очень надеемся, что да. Но даже если у вас нет ответа на этот вопрос, это не проблема. Понять, что такое логарифм очень просто. Почему именно 4? В такую степень нужно возвести число 3, чтобы получилось 81. Когда вы поняли принцип, можно приступать и к более сложным вычислениям. Неравенства вы проходили еще несколько лет назад. И с тех пор они постоянно встречаются вам в математике. Если у вас проблемы с решением неравенств, ознакомьтесь с соответствующим разделом. Самое простое логарифмическое неравенство. Простейшие логарифмические неравенства не ограничиваются этим примером, есть еще три, только с другими знаками. Зачем это нужно? Чтобы полнее понять, как решать неравенство с логарифмами. Теперь приведем более применимый пример, все еще достаточно простой, сложные логарифмические неравенства оставим на потом. Как это решить? Все начинается с ОДЗ. О нем стоит знать больше, если хочется всегда легко решать любое неравенство. Аббревиатура расшифровывается как область допустимых значений. В заданиях для ЕГЭ нередко всплывает данная формулировка. ОДЗ пригодится вам не только в случае логарифмических неравенств. Посмотрите еще раз на вышеприведенный пример. Мы будем рассматривать ОДЗ, исходя из него, чтобы вы поняли принцип, и решение логарифмических неравенств не вызывало вопросов. Из определения логарифма следует что, 2х+4 должно быть больше нуля. В нашем случае это означает следующее. Это число по определению должно быть положительным. Решите неравенство, представленное выше. Это можно сделать даже устно, здесь явно, что X не может быть меньше 2. Решение неравенства и будет определением области допустимых значений. Отбрасываем из обеих частей неравенства сами логарифмы. Что в результате у нас остается? Простое неравенство. Решить его несложно. X должен быть больше -0,5. Теперь совмещаем два полученных значения в систему. Таким образом, Это и будет область допустимых значений для рассматриваемого логарифмического неравенства. Зачем вообще нужно ОДЗ? Это возможность отсеять неверные и невозможные ответы. Если ответ не входит в область допустимых значений, значит, ответ попросту не имеет смысла. Это стоит запомнить надолго, так как в ЕГЭ часто встречается необходимость поиска ОДЗ, и касается она не только логарифмических неравенств. Решение состоит из нескольких этапов. Во-первых, необходимо найти область допустимых значений. В ОДЗ будет два значения, это мы рассмотрели выше. Далее нужно решить само неравенство. Методы решения бывают следующими: В зависимости от ситуации стоит применять один из вышеперечисленных методов. Перейдем непосредственно к решению. Раскроем наиболее популярный метод, который подходит для решения заданий ЕГЭ практически во всех случаях. Далее мы рассмотрим метод декомпозиции. Он может помочь, если попалось особенно «заковыристое» неравенство. Итак, алгоритм решения логарифмического неравенства. Примеры решения
: Мы не зря взяли именно такое неравенство! Обратите внимание на основание. Запомните: если оно больше единицы, знак остается прежним при нахождении области допустимых значений; в противном случае нужно изменить знак неравенства. В результате мы получаем неравенство: Теперь приводим левую часть к виду уравнения, равному нулю. Вместо знака «меньше» ставим «равно», решаем уравнение. Таким образом, мы найдем ОДЗ. Надеемся, что с решением такого простого уравнения у вас не будет проблем. Ответы -4 и -2. Это еще не все. Нужно отобразить эти точки на графике, расставить «+» и «-». Что нужно для этого сделать? Подставить в выражение числа из интервалов. Где значения положительны, там ставим «+». Ответ
: х не может быть больше -4 и меньше -2. Мы нашли область допустимых значений только для левой части, теперь нужно найти область допустимых значений правой части. Это не в пример легче. Ответ: -2. Пересекаем обе полученные области. И только теперь начинаем решать само неравенство. Упростим его, насколько возможно, чтобы решать было легче. Снова применяем метод интервалов в решении. Опустим выкладки, с ним уже и так все понятно по предыдущему примеру. Ответ. Но этот метод подходит, если логарифмическое неравенство имеет одинаковые основания. Решение логарифмических уравнений и неравенств с разными основаниями предполагает изначальное приведение к одному основанию. Далее применяйте вышеописанный метод. Но есть и более сложный случай. Рассмотрим один из самых сложных видов логарифмических неравенств. Как решать неравенства с такими характеристиками? Да, и такие могут встретиться в ЕГЭ. Решение неравенств нижеследующим способом тоже полезно скажется на вашем образовательном процессе. Разберемся в вопросе подробным образом. Отбросим теорию, перейдем сразу к практике. Чтобы решать логарифмические неравенства, достаточно однажды ознакомиться с примером. Чтобы решить логарифмическое неравенство представленного вида, необходимо привести правую часть к логарифму с тем же основанием. Принцип напоминает равносильные переходы. В итоге неравенство будет выглядеть следующим образом. Собственно, остается создать систему неравенств без логарифмов. Используя метод рационализации, переходим к равносильной системе неравенств. Вы поймете и само правило, когда подставите соответствующие значения и проследите их изменения. В системе будут следующие неравенства. Воспользовавшись методом рационализации при решении неравенств нужно помнить следующее: из основания необходимо вычесть единицу, х по определению логарифма из обеих частей неравенства вычитается (правое из левого), два выражения перемножаются и выставляются под исходным знаком по отношению к нулю. Дальнейшее решение осуществляется методом интервалов, здесь все просто. Вам важно понять отличия в методах решения, тогда все начнет легко получаться. В логарифмических неравенствах много нюансов. Простейшие из них решать достаточно легко. Как сделать так, чтобы решать каждое из них без проблем? Все ответы вы уже получили в этой статье. Теперь впереди вас ждет длительная практика. Постоянно практикуйтесь в решении самых разных задач в рамках экзамена и сможете получить наивысший балл. Успехов вам в вашем непростом деле!
Решение примеров
3x > 24;
х > 8.
Что необходимо для решения логарифмических неравенств?
Домашнее задание
и окончательный ответ к системе имеет вид: 
Сергей Валерьевич
© Народная мудрость
Теперь, когда мы познакомились с понятиями по отдельности, перейдем к их рассмотрению в общем.
Что такое ОДЗ? ОДЗ для логарифмических неравенств
Теперь перейдем к решению простейшего логарифмического неравенства.
Алгоритм решения логарифмического неравенства
Логарифмические неравенства с переменным основанием
