Написать уравнение касательной параллельной прямой. Уравнение касательной к графику функции. Исчерпывающий гид (2019) Уравнение касательной к графику функции

Касательная – это прямая, проходящая через точку кривой и совпадающая с ней в этой точке с точностью до первого порядка (рис.1).

Другое определение: это предельное положение секущей при Δx→0.

Пояснение: Возьмем прямую, пересекающую кривую в двух точках: А и b (см.рисунок). Это секущая. Будем поворачивать ее по часовой стрелке до тех пор, пока она не обретет только одну общую точку с кривой. Так мы получим касательную.

Строгое определение касательной:

Касательная к графику функции f, дифференцируемой в точке x о, — это прямая, проходящая через точку (x о; f(x о)) и имеющая угловой коэффициент f′(x о).

Угловой коэффициент имеет прямая вида y =kx +b. Коэффициент k и является угловым коэффициентом этой прямой.

Угловой коэффициент равен тангенсу острого угла, образуемого этой прямой с осью абсцисс:

k = tg α

Здесь угол α – это угол между прямой y =kx +b и положительным (то есть против часовой стрелки) направлением оси абсцисс. Он называется углом наклона прямой(рис.1 и 2).Если угол наклона прямой y =kx +b острый, то угловой коэффициент является положительным числом. График возрастает (рис.1).

Если угол наклона прямой y =kx +b тупой, то угловой коэффициент является отрицательным числом. График убывает (рис.2).

Если прямая параллельна оси абсцисс, то угол наклона прямой равен нулю. В этом случае угловой коэффициент прямой тоже равен нулю (так как тангенс нуля есть ноль). Уравнение прямой будет иметь вид y = b (рис.3).

Если угол наклона прямой равен 90º (π/2), то есть она перпендикулярна оси абсцисс, то прямая задается равенством x =c, где c – некоторое действительное число (рис.4).

Уравнение касательной к графику функцииy =f(x) в точке x о:

Пример: Найдем уравнение касательной к графику функции f(x) = x 3 – 2x 2 + 1 в точке с абсциссой 2.

Решение.

Следуем алгоритму.

1) Точка касания x оравна 2. Вычислим f(x о):

f(x о) = f(2) = 2 3 – 2 ∙ 2 2 + 1 = 8 – 8 + 1 = 1

2) Находим f′(x). Для этого применяем формулы дифференцирования, изложенные в предыдущем разделе. Согласно этим формулам, х 2 = 2х, а х 3 = 3х 2 . Значит:

f′(x) = 3х 2 – 2 ∙ 2х = 3х 2 – 4х.

Теперь, используя полученное значение f′(x), вычислим f′(x о):

f′(x о) = f′(2) = 3 ∙ 2 2 – 4 ∙ 2 = 12 – 8 = 4.

3) Итак, у нас есть все необходимые данные: x о = 2, f(x о) = 1, f′(x о) = 4. Подставляем эти числа в уравнение касательной и находим окончательное решение:

у = f(x о) + f′(x о) (x – x о) = 1 + 4 ∙ (х – 2) = 1 + 4х – 8 = –7 + 4х = 4х – 7.

Ответ: у = 4х – 7.

Уравнение касательной к графику функции

П. Романов, Т. Романова, г. Магнитогорск, Челябинская обл.

Статья опубликована при поддержке Гостиничного комплекса «ИТАКА+». Останавливаясь в городе судостроителей Северодвинске, вы не столкнетесь с проблемой поиска временного жилья. , на сайте гостиничного комплекса «ИТАКА+» http://itakaplus.ru, вы сможете легко и быстро снять квартиру в городе, на любой срок, с посуточной оплатой.

На современном этапе развитияобразования в качестве одной из основных егозадач выступает формирование творчески мыслящейличности. Способность же к творчеству у учащихсяможет быть развита лишь при условиисистематического привлечения их к основамисследовательской деятельности. Фундаментом дляприменения учащимися своих творческих сил,способностей и дарований являютсясформированные полноценные знания и умения. Всвязи с этим проблема формирования системыбазовых знаний и умений по каждой теме школьногокурса математики имеет немаловажное значение.При этом полноценные умения должны являтьсядидактической целью не отдельных задач, атщательно продуманной их системы. В самомшироком смысле под системой понимаетсясовокупность взаимосвязанных взаимодействующихэлементов, обладающая целостностью и устойчивойструктурой.

Рассмотрим методику обученияучащихся составлению уравнения касательной кграфику функции. По существу, все задачи наотыскание уравнения касательной сводятся кнеобходимости отбора из множества (пучка,семейства) прямых тех из них, которыеудовлетворяют определенному требованию– являются касательными к графику некоторойфункции. При этом множество прямых, из которогоосуществляется отбор, может быть задано двумяспособами:

а) точкой, лежащей на плоскости xOy (центральный пучок прямых); б) угловым коэффициентом (параллельный пучок прямых).

В связи с этим при изучениитемы «Касательная к графику функции» с цельювычленения элементов системы нами были выделеныдва типа задач:

1) задачи на касательную, заданную точкой, через которую она проходит; 2) задачи на касательную, заданную ее угловым коэффициентом.

Обучение решению задач накасательную осуществлялось при помощиалгоритма, предложенного А.Г. Мордковичем .Его принципиальное отличие от уже известныхзаключается в том, что абсцисса точки касанияобозначается буквой a (вместо x0), в связи с чемуравнение касательной приобретает вид

y = f(a) + f «(a)(x – a)

(сравните с y = f(x 0) + f «(x 0)(x– x 0)). Этот методический прием, на нашвзгляд, позволяет учащимся быстрее и легчеосознать, где в общем уравнении касательнойзаписаны координаты текущей точки, а где– точки касания.

Алгоритмсоставления уравнения касательной к графикуфункции y = f(x)

1. Обозначить буквой a абсциссу точки касания. 2. Найти f(a). 3. Найти f «(x) и f «(a). 4. Подставить найденные числа a, f(a), f «(a) в общее уравнение касательной y = f(a) = f «(a)(x – a).

Этот алгоритм может бытьсоставлен на основе самостоятельного выделенияучащимися операций и последовательности ихвыполнения.

Практика показала, чтопоследовательное решение каждой из ключевыхзадач при помощи алгоритма позволяетформировать умения написания уравнениякасательной к графику функции поэтапно, а шагиалгоритма служат опорными пунктами действий.Данный подход соответствует теории поэтапногоформирования умственных действий, разработаннойП.Я. Гальпериным и Н.Ф. Талызиной .

В первом типе задач быливыделены две ключевые задачи:

• касательная проходит через точку, лежащую на кривой (задача 1);
• касательная проходит через точку, не лежащую на кривой (задача 2).

Задача 1. Составьте уравнениекасательной к графику функции в точке M(3; – 2).

Решение. Точка M(3; – 2)является точкой касания, так как

1. a = 3 – абсцисса точки касания. 2. f(3) = – 2. 3. f «(x) = x 2 – 4, f «(3) = 5. y = – 2 + 5(x – 3), y = 5x – 17 – уравнение касательной.

Задача 2. Напишите уравнениявсех касательных к графику функции y = – x 2– 4x + 2, проходящих через точку M(– 3; 6).

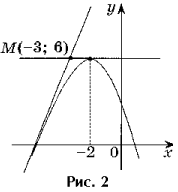Решение. Точка M(– 3; 6) неявляется точкой касания, так как f(– 3)­ 6 (рис. 2).

2. f(a) = – a 2 – 4a + 2. 3. f «(x) = – 2x – 4, f «(a) = – 2a – 4. 4. y = – a 2 – 4a + 2 – 2(a + 2)(x – a) – уравнение касательной.

Касательная проходит черезточку M(– 3; 6), следовательно, ее координатыудовлетворяют уравнению касательной.

6 = – a 2 – 4a + 2 – 2(a + 2)(– 3 – a), a 2 + 6a + 8 = 0^ a 1 = – 4, a 2 = – 2.

Если a = – 4, то уравнениекасательной имеет вид y = 4x + 18.

Если a = – 2, то уравнениекасательной имеет вид y = 6.

Во втором типе ключевымизадачами будут следующие:

• касательная параллельна некоторой прямой (задача 3);
• касательная проходит под некоторым углом к данной прямой (задача 4).

Задача 3. Напишите уравнениявсех касательных к графику функции y = x 3 – 3x 2+ 3, параллельных прямой y = 9x + 1.

Решение.

1. a – абсцисса точки касания. 2. f(a) = a 3 – 3a 2 + 3. 3. f «(x) = 3x 2 – 6x, f «(a) = 3a 2 – 6a.

Но, с другой стороны, f «(a) = 9(условие параллельности). Значит, надо решитьуравнение 3a 2 – 6a = 9. Его корни a = – 1, a = 3(рис. 3).

4. 1) a = – 1; 2) f(– 1) = – 1; 3) f «(– 1) = 9; 4) y = – 1 + 9(x + 1);

y = 9x + 8 – уравнениекасательной;

1) a = 3; 2) f(3) = 3; 3) f «(3) = 9; 4) y = 3 + 9(x – 3);

y = 9x – 24 – уравнениекасательной.

Задача 4. Напишите уравнениекасательной к графику функции y = 0,5x 2 – 3x + 1,проходящей под углом 45° к прямой y = 0 (рис. 4).

Решение. Из условия f «(a) =tg 45° найдем a: a – 3 = 1^ a = 4.

1. a = 4 – абсцисса точки касания. 2. f(4) = 8 – 12 + 1 = – 3. 3. f «(4) = 4 – 3 = 1. 4. y = – 3 + 1(x – 4).

y = x – 7 – уравнениекасательной.

Несложно показать, чторешение любой другой задачи сводится к решениюодной или нескольких ключевых задач. Рассмотримв качестве примера следующие две задачи.

1. Напишите уравнениякасательных к параболе y = 2x 2 – 5x – 2, есликасательные пересекаются под прямым углом и однаиз них касается параболы в точке с абсциссой 3(рис. 5).

Решение. Поскольку данаабсцисса точки касания, то первая часть решениясводится к ключевой задаче 1.

1. a = 3 – абсцисса точки касания одной из сторон прямого угла. 2. f(3) = 1. 3. f «(x) = 4x – 5, f «(3) = 7. 4. y = 1 + 7(x – 3), y = 7x – 20 – уравнение первой касательной.

Пустьa – угол наклона первойкасательной. Так как касательныеперпендикулярны, то – угол наклона второй касательной. Изуравнения y = 7x – 20 первой касательной имеем tga = 7. Найдем

Это значит, что угловойкоэффициент второй касательной равен .

Дальнейшее решение сводится кключевой задаче 3.

Пусть B(c; f(c)) есть точкакасания второй прямой, тогда

1. – абсцисса второй точки касания. 2. 3. 4. – уравнение второй касательной.

Примечание. Угловойкоэффициент касательной может быть найден проще,если учащимся известно соотношениекоэффициентов перпендикулярных прямых k 1 k 2= – 1.

2. Напишите уравнения всехобщих касательных к графикам функций

Решение. Задача сводится котысканию абсцисс точек касания общихкасательных, то есть к решению ключевой задачи 1 вобщем виде, составлению системы уравнений ипоследующему ее решению (рис. 6).

1. Пусть a – абсцисса точки касания, лежащей на графике функции y = x 2 + x + 1. 2. f(a) = a 2 + a + 1. 3. f «(a) = 2a + 1. 4. y = a 2 + a + 1 + (2a + 1)(x – a) = (2a + 1)x + 1 – a 2 .

1. Пусть c – абсцисса точки касания, лежащей на графике функции 2. 3. f «(c) = c. 4.

Так как касательные общие, то

Итак, y = x + 1 и y = – 3x – 3– общие касательные.

Основная цель рассмотренныхзадач – подготовить учащихся ксамостоятельному распознаванию типа ключевойзадачи при решении более сложных задач,требующих определенных исследовательскихумений (умения анализировать, сравнивать,обобщать, выдвигать гипотезу и т. д.). К числутаких задач можно отнести любую задачу, в которуюключевая задача входит как составляющая.Рассмотрим в качестве примера задачу (обратнуюзадаче 1) на нахождение функции по семейству еекасательных.

3. При каких b и c прямые y = x иy = – 2x являются касательными к графику функцииy = x 2 + bx + c?

Решение.

Пусть t – абсцисса точкикасания прямой y = x с параболой y = x 2 + bx + c; p– абсцисса точки касания прямой y = – 2x спараболой y = x 2 + bx + c. Тогда уравнениекасательной y = x примет вид y = (2t + b)x + c – t 2 , ауравнение касательной y = – 2x примет вид y = (2p +b)x + c – p 2 .

Составим и решим системууравнений

Ответ:

Задачи длясамостоятельного решения

1. Напишите уравнениякасательных, проведенных к графику функции y = 2x 2– 4x + 3 в точках пересечения графика с прямой y = x +3.

Ответ: y = – 4x + 3, y = 6x – 9,5.

2. При каких значениях aкасательная, проведенная к графику функции y = x 2– ax в точке графика с абсциссой x 0 = 1,проходит через точку M(2; 3)?

Ответ: a = 0,5.

3. При каких значениях pпрямая y = px – 5 касается кривой y = 3x 2 – 4x – 2?

Ответ: p 1 = – 10, p 2= 2.

4. Найдите все общие точкиграфика функции y = 3x – x 3 и касательной,проведенной к этому графику через точку P(0; 16).

Ответ: A(2; – 2), B(– 4; 52).

5. Найдите кратчайшеерасстояние между параболой y = x 2 + 6x + 10 ипрямой

Ответ:

6. На кривой y = x 2 – x + 1найдите точку, в которой касательная к графикупараллельна прямой y – 3x + 1 = 0.

Ответ: M(2; 3).

7. Напишите уравнениекасательной к графику функции y = x 2 + 2x –| 4x |, которая касается его в двух точках.Сделайте чертеж.

Ответ: y = 2x – 4.

8. Докажите, что прямая y = 2x– 1 не пересекает кривую y = x 4 + 3x 2 + 2x.Найдите расстояние между их ближайшими точками.

Ответ:

9. На параболе y = x 2взяты две точки с абсциссами x 1 = 1, x 2 = 3.Через эти точки проведена секущая. В какой точкепараболы касательная к ней будет параллельнапроведенной секущей? Напишите уравнения секущейи касательной.

Ответ: y = 4x – 3 – уравнениесекущей; y = 4x – 4 – уравнение касательной.

10. Найдите уголq между касательнымик графику функции y = x 3 – 4x 2 + 3x + 1,проведенными в точках с абсциссами 0 и 1.

Ответ:q = 45°.

11. В каких точкахкасательная к графику функции образует с осью Ox угол в 135°?

Ответ: A(0; – 1), B(4; 3).

12. В точке A(1; 8) к кривой проведенакасательная. Найдите длину отрезка касательной,заключенного между осями координат.

Ответ:

13. Напишите уравнение всехобщих касательных к графикам функций y = x 2 –x + 1 и y = 2x 2 – x + 0,5.

Ответ: y = – 3x и y = x.

14. Найдите расстояние междукасательными к графику функции параллельными оси абсцисс.

Ответ:

15. Определите, под какимиуглами парабола y = x 2 + 2x – 8 пересекает осьабсцисс.

Ответ:q 1 = arctg 6,q 2 = arctg (– 6).

16. На графике функции найдите всеточки, касательная в каждой из которых к этомуграфику пересекает положительные полуосикоординат, отсекая от них равные отрезки.

Ответ: A(– 3; 11).

17. Прямая y = 2x + 7 и парабола y= x 2 – 1 пересекаются в точках M и N. Найдитеточку K пересечения прямых, касающихся параболы вточках M и N.

Ответ: K(1; – 9).

18. При каких значениях bпрямая y = 9x + b является касательной к графикуфункции y = x 3 – 3x + 15?

Ответ: – 1; 31.

19. При каких значениях kпрямая y = kx – 10 имеет только одну общую точку сграфиком функции y = 2x 2 + 3x – 2? Для найденныхзначений k определите координаты точки.

Ответ: k 1 = – 5, A(– 2;0); k 2 = 11, B(2; 12).

20. При каких значениях bкасательная, проведенная к графику функции y = bx 3– 2x 2 – 4 в точке с абсциссой x 0 = 2,проходит через точку M(1; 8)?

Ответ: b = – 3.

21. Парабола с вершиной наоси Ox касается прямой, проходящей через точки A(1;2) и B(2; 4), в точке B. Найдите уравнение параболы.

Ответ:

22. При каком значениикоэффициента k парабола y = x 2 + kx + 1 касаетсяоси Ox?

Ответ: k =д 2.

23. Найдите углы междупрямой y = x + 2 и кривой y = 2x 2 + 4x – 3.

29. Найдите расстояние междукасательными к графику функции образующими сположительным направлением оси Ox угол 45°.

Ответ:

30. Найдите геометрическоеместо вершин всех парабол вида y = x 2 + ax + b,касающихся прямой y = 4x – 1.

Ответ: прямая y = 4x + 3.

Литература

1. Звавич Л.И., Шляпочник Л.Я., Чинкина М.В. Алгебра и начала анализа: 3600 задач для школьников и поступающих в вузы. – М., Дрофа, 1999. 2. Мордкович А. Семинар четвертый для молодых учителей. Тема «Приложения производной». – М., «Математика», № 21/94. 3. Формирование знаний и умений на основе теории поэтапного усвоения умственных действий. / Под ред. П.Я. Гальперина, Н.Ф. Талызиной. – М., МГУ, 1968.

Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.

Сбор и использование персональной информации

Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.

От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.

Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.

Какую персональную информацию мы собираем:

• Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.

Как мы используем вашу персональную информацию:

• Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
• Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
• Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
• Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.

Раскрытие информации третьим лицам

Мы не раскрываем полученную от Вас информацию третьим лицам.

Исключения:

• В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
• В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.

Защита персональной информации

Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.

Соблюдение вашей конфиденциальности на уровне компании

Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.

Видеоурок «Уравнение касательной к графику функции» демонстрирует учебный материал для освоения темы. В ходе видеоурока представлен теоретический материал, необходимый для формирования понятия об уравнении касательной к графику функции в данной точке, алгоритм нахождения такой касательной, описаны примеры решения задач с использованием изученного теоретического материала.

В видеоуроке используются методы, улучшающие наглядность материала. В представлении вставлены рисунки, схемы, даются важные голосовые комментарии, применяется анимация, выделение цветом и другими инструментами.

Видеоурок начинается с представления темы урока и изображения касательной к графику некоторой функции y=f(x) в точке M(a;f(a)). Известно, что угловой коэффициент касательной, построенной к графику в данной точке, равен производной функции f΄(a) в данной точке. Также из курса алгебры известно уравнение прямой y=kx+m. Схематично представлено решение задачи нахождения уравнения касательной в точке, которая сводится к нахождению коэффициентов k, m. Зная координаты точки, принадлежащей графику функции, можем найти m, подставив значение координат в уравнение касательной f(a)=ka+m. Из него находим m=f(a)-ka. Таким образом, зная значение производной в данной точке и координаты точки, можно представить уравнение касательной таким образом y=f(a)+f΄(a)(x-a).

Далее рассматривается пример составления уравнения касательной, следуя схеме. Дана функция y=x 2 , x=-2. Приняв а=-2, находим значение функции в данной точке f(a)= f(-2)=(-2) 2 =4. Определяем производную функции f΄(х)=2х. В данной точке производная равна f΄(a)= f΄(-2)=2·(-2)=-4. Для составления уравнения найдены все коэффициенты а=-2, f(a)=4, f΄(a)=-4, поэтому уравнение касательной у=4+(-4)(х+2). Упростив уравнение, получаем у=-4-4х.

В следующем примере предлагается составить уравнение касательной в начале координат к графику функции y=tgx. В данной точке а=0, f(0)=0, f΄(х)=1/cos 2 x, f΄(0)=1. Таким образом, уравнение касательной выглядит у=х.

В качестве обобщения процесс составления уравнения касательной к графику функции в некоторой точке оформляется в виде алгоритма, состоящего из 4 шагов:

• Вводится обозначение а абсциссы точки касания;
• Вычисляется f(a);
• Определяется f΄(х) и вычисляется f΄(a). В формулу уравнения касательной y=f(a)+f΄(a)(x-a) подставляются найденные значения а, f(a), f΄(a).

В примере 1 рассматривается составление уравнения касательной к графику функции у=1/х в точке х=1. Для решения задачи пользуемся алгоритмом. Для данной функции в точке а=1 значение функции f(a)=-1. Производная функции f΄(х)=1/х 2 . В точке а=1 производная f΄(a)= f΄(1)=1. Используя полученные данные, составляется уравнение касательной у=-1+(х-1), или у=х-2.

В примере 2 необходимо найти уравнение касательной к графику функции у=х 3 +3х 2 -2х-2. Основное условие — параллельность касательной и прямой у=-2х+1. Сначала находим угловой коэффициент касательной, равный угловому коэффициенту прямой у=-2х+1. Так как f΄(a)=-2 для данной прямой, то k=-2 и для искомой касательной. Находим производную функции (х 3 +3х 2 -2х-2)΄=3х 2 +6х-2. Зная, что f΄(a)=-2, находим координаты точки 3а 2 +6а-2=-2. Решив уравнение, получаем а 1 =0, а 2 =-2. Используя найденные координаты, можно найти уравнение касательной с помощью известного алгоритма. Находим значение функции в точках f(а 1)=-2, f(а 2)=-18. Значение производной в точке f΄(а 1)= f΄(а 2)=-2. Подставив найденные значения в уравнение касательной, получим для первой точки а 1 =0 у=-2х-2, а для второй точки а 2 =-2 уравнение касательной у=-2х-22.

В примере 3 описывается составление уравнения касательной для ее проведения в точке (0;3) к графику функции y=√x. Решение производится по известному алгоритму. Точка касания имеет координаты х=а, где а>0. Значение функции в точке f(a)=√x. Производная функции f΄(х)=1/2√х, поэтому в данной точке f΄(а)=1/2√а. Подставив все полученные значения в уравнение касательной, получаем у=√а+(х-а)/2√а. Преобразовав уравнение, получаем у=х/2√а+√а/2. Зная, что касательная проходит через точку (0;3), находим значение а. Находим а из 3=√а/2. Отсюда √а=6, а=36. Находим уравнение касательной у=х/12+3. На рисунке изображается график рассматриваемой функции и построенная искомая касательная.

Ученикам напоминаются приближенные равенства Δy=≈f΄(x)Δxи f(x+Δx)-f(x)≈f΄(x)Δx. Принимая х=а, x+Δx=х, Δx=х-а, получаем f(х)- f(а)≈f΄(а)(х-а), отсюда f(х)≈f(а)+f΄(а)(х-а).

В примере 4 необходимо найти приближенное значение выражение 2,003 6 . Так как необходимо отыскать значение функции f(х)=х 6 в точке х=2,003, можем воспользоваться известной формулой, приняв f(х)=х 6 , а=2, f(а)= f(2)=64, f΄(x)=6х 5 . Производная в точке f΄(2)=192. Поэтому 2,003 6 ≈65-192·0,003. Вычислив выражение, получаем 2,003 6 ≈64,576.

Видеоурок «Уравнение касательной к графику функции» рекомендуется использовать на традиционном уроке математики в школе. Учителю, осуществляющему обучению дистанционно, видеоматериал поможет более понятно объяснить тему. Видео может быть рекомендовано для самостоятельного рассмотрения учениками при необходимости углубить их понимание предмета.

ТЕКСТОВАЯ РАСШИФРОВКА:

Нам известно, что если точка М (а; f(а)) (эм с координатами а и эф от а) принадлежит графику функции у =f (x) и если в этой точке к графику функции можно провести касательную, не перпендикулярную к оси абсцисс, то угловой коэффициент касательной равен f»(a) (эф штрих от а).

Пусть даны функция у = f(x) и точка М (a; f(a)), a также известно, что существует f´(a). Составим уравнение касательной к графику заданной функции в заданной точке. Это уравнение, как уравнение любой прямой, не параллельной оси ординат, имеет вид y = kx+m (игрек равный ка икс плюс эм), поэтому задача состоит в отыскании значений коэффициентов k и m.(ка и эм)

Угловой коэффициент k= f»(a). Для вычисления значения m воспользуемся тем, что искомая прямая проходит через точку М(а; f (а)). Это значит, что, если подставить координаты точки М в уравнение прямой, получим верное равенство: f(a) = ka+m, откуда находим, что m = f(a) — ka.

Осталось подставить найденные значения коэффициентов kи mв уравнение прямой:

y = kx+(f(a) -ka);

y = f(a)+k(x-a);

y=f(a)+f«(a) (x—a).(игрек равен эф от а плюс эф штрих от а, умноженный на икс минус а).

Нами получено уравнение касательной к графику функции y = f(x) в точке х=а.

Если, скажем, у = х 2 и х= -2 (т.е. а = -2), то f(а) = f(-2) = (-2) 2 =4; f´(x) = 2х, значит, f»(a) = f´(-2) = 2·(-2) = -4. (то эф от а равно четыре, эф штрих от икс равно два икс, значит эф штрих от а равно минус четыре)

Подставив в уравнение найденные значения a = -2, f(a) = 4, f»(a) = -4, получим: у = 4+(-4)(х+2), т.е. у = -4х-4.

(игрек равен минус четыре икс минус четыре)

Составим уравнение касательной к графику функции у = tgx(игрек равен тангенс икс) в начале координат. Имеем: а = 0, f(0) = tg0=0;

f»(x)= , значит, f»(0) = l. Подставив в уравнение найденные значения а=0, f(a)=0, f´(a) = 1, получим: у=х.

Обобщим наши шаги нахождения уравнения касательной к графику функции в точке х с помощью алгоритма.

АЛГОРИТМ СОСТАВЛЕНИЯ УРАВНЕНИЯ КАСАТЕЛЬНОЙ К ГРАФИКУ ФУНКЦИИ у = f(x):

1) Обозначить абсциссу точки касания буквой а.

2) Вычислить f (а).

3) Найти f´(x) и вычислить f´(a).

4) Подставить найденные числа a, f(a), f´(а) в формулуy=f(a)+f«(a) (x—a).

Пример 1. Составить уравнение касательной к графику функции у = — в

точке х = 1.

Решение. Воспользуемся алгоритмом, учитывая, что в данном примере

2) f(a)=f(1)=- =-1

3) f´(x)=; f´(a)= f´(1)= =1.

4) Подставим найденные три числа: а = 1, f(а) = -1, f»(а) = 1 в формулу. Получим: у = -1+(х-1), у = х-2.

Ответ: у = х-2.

Пример 2. Дана функция у = х 3 +3х 2 -2х-2. Записать уравнение касательной к графику функции у= f(х), параллельной прямой у = -2х +1.

Используя алгоритм составления уравнения касательной, учтем, что в данном примере f(x) = х 3 +3х 2 -2х-2, но здесь не указана абсцисса точки касания.

Начнем рассуждать так. Искомая касательная должна быть параллельна прямой у = -2х+1. А параллельные прямые имеют равные угловые коэффициенты. Значит, угловой коэффициент касательной равен угловому коэффициенту заданной прямой: k кас. = -2. Hok кас. = f»(a). Таким образом, значение а мы можем найти из уравнения f ´(а) = -2.

Найдем производную функции у=f(x):

f«(x)= (х 3 +3х 2 -2х-2)´ =3х 2 +6х-2;f«(а)= 3а 2 +6а-2.

Из уравнения f»(а) = -2, т.е. 3а 2 +6а-2 =-2 находим а 1 =0, a 2 =-2. Значит, имеются две касательные, удовлетворяющие условию задачи: одна в точке с абсциссой 0, другая в точке с абсциссой -2.

Теперь можно действовать по алгоритму.

1) а 1 =0, а 2 =-2.

2) f(a 1)= 0 3 +3·0 2 -2∙0-2=-2; f(a 2)=(-2) 3 +3·(-2) 2 -2·(-2)-2=6;

3) f»(a 1) = f»(a 2) = -2.

4) Подставив значения a 1 = 0, f(a 1) =-2, f»(a 1) = -2 в формулу, получим:

у=-2-2(х-0), у=-2х-2.

Подставив значения а 2 =-2, f(a 2) =6, f»(a 2)= -2 в формулу, получим:

у=6-2(х+2), у=-2х+2.

Ответ: у=-2х-2, у=-2х+2.

Пример 3. Из точки (0; 3) провести касательную к графику функции у = . Решение. Воспользуемся алгоритмом составления уравнения касательной, учитывая, что в данном примере f(x) = . Заметим, что и здесь, как в примере 2, не указана явно абсцисса точки касания. Тем не менее, действуем по алгоритму.

1) Пусть х = а — абсцисса точки касания; ясно, что а >0.

3) f´(x)=()´=; f´(a) =.

4) Подставив значения a, f(a) = , f»(a) = в формулу

y=f (a) +f «(a) (x-a), получим:

По условию касательная проходит через точку (0; 3). Подставив в уравнение значения х = 0, у = 3, получим: 3 = , и далее =6, a =36.

Как видите, в этом примере только на четвертом шаге алгоритма нам удалось найти абсциссу точки касания. Подставив значение a =36 в уравнение, получим: y=+3

На рис. 1 представлена геометрическая иллюстрация рассмотренного примера: построен график функции у =, проведена прямая у = +3.

Ответ: у = +3.

Нам известно, что для функции y = f(x), имеющей производную в точке х, справедливо приближенное равенство: Δyf´(x)Δx (дельта игрек приближенно равно эф штрих от икс, умноженное на дельта икс)

или, подробнее, f(x+Δx)-f(x) f´(x) Δx (эф от икс плюс дельта икс минус эф от икс приближенно равно эф штрих от икс на дельта икс).

Для удобства дальнейших рассуждений изменим обозначения:

вместо х будем писать а,

вместо х+Δxбудем писать х

вместо Δх будем писать х-а.

Тогда написанное выше приближенное равенство примет вид:

f(x)-f(a)f´(a)(x-a)

f(x)f(a)+f´(a)(x-a). (эф от икс приближенно равно эф от а плюс эф штрих от а, умноженное на разность икса и а).

Пример 4. Найти приближенное значение числового выражения 2,003 6 .

Решение. Речь идет об отыскании значения функции у = х 6 в точке х = 2,003. Воспользуемся формулой f(x)f(a)+f´(a)(x-a), учтя, что в данном примере f(x)=x 6 , a = 2,f(a) = f(2) = 2 6 =64; x = 2,003, f»(x) = 6x 5 и, следовательно, f»(а) = f»(2) = 6·2 5 =192.

В итоге получаем:

2,003 6 64+192· 0,003, т.е. 2,003 6 =64,576.

Если мы воспользуемся калькулятором, то получим:

2,003 6 = 64,5781643…

Как видите, точность приближения вполне приемлема.

У = f(х) и если в этой точке к графику функции можно провести касательную, не перпендикулярную к оси абсцисс, то угловой коэффициент касательной равен f»(а). Мы этим уже несколько раз пользовались. Например, в § 33 было установлено, что график функции у = sin х(синусоида) в начале координат образует с осью абсцисс угол 45° (точнее, касательная к графику в начале координат составляет с положительным направлением оси х угол 45°), а в примере 5 § 33 были найдены точки на графике заданной функции, в которых касательная параллельна оси абсцисс. В примере 2 § 33 было составлено уравнение касательной к графику функции у = х 2 в точке х = 1 (точнее, в точке (1; 1), но чаще указывают только значение абсциссы, полагая, что если значение абсциссы известно, то значение ординаты можно найти из уравнения у = f(х)). В этом параграфе мы выработаем алгоритм составления уравнения касательной.к графику любой функции.

Пусть даны функция у = f(х) и точка М (а; f(а)), а также известно, что существует f»(а). Составим уравнение касательной к графику заданной функции в заданной точке. Это уравнение, как уравнение любой прямой, не параллельной оси ординат, имеет вид у = кх+m, поэтому задача состоит в отыскании значений коэффициентов к и m.

С угловым коэффициентом к проблем нет: мы знаем, что к = f»(а). Для вычисления значения т воспользуемся тем, что искомая прямая проходит через точку М(а; f (а)). Это значит, что, если подставить координаты точки М в уравнение прямой, получим верное равенство: f(а) = ка+m, откуда находим, что m = f(а) — ка.Осталось подставить найденные значения коэффициентов кит в уравнение прямой:

Нами получено уравнение касательной к графику функции у = f(х) в точке х=а.Если, скажем, Подставив в уравнение (1) найденные значения а = 1, f(а) = 1 f»(а) = 2, получим: у = 1+2(х-f), т.е. у = 2х-1.Сравните этот результат с тем, что был получен в примере 2 из § 33. Естественно, получилось то же самое.Составим уравнение касательной к графику функции у = tg х в начале координат. Имеем: значит, соs х f»(0) = 1. Подставив в уравнение (1) найденные значения а= 0, f(а)= 0, f»(а) = 1, получим: у=х.Именно поэтому мы и провели тангенсоиду в § 15 (см. рис. 62) через начало координат под углом 45° к оси абсцисс.Решая эти достаточно простые примеры, мы фактически пользовались определенным алгоритмом, который заложен в формуле (1). Сделаем этот алгоритм явным.

АЛГОРИТМ СОСТАВЛЕНИЯ УРАВНЕНИЯ КАСАТЕЛЬНОЙ К ГРАФИКУ ФУНКЦИИ у = f(x)

1) Обозначить абсциссу точки касания буквой а.2) Вычислить 1 (а).3) Найти f»(х) и вычислить f»(а).4) Подставить найденные числа а, f(а), (а) в формулу (1).

Пример 1. Составить уравнение касательной к графику функции в точке х = 1. Воспользуемся алгоритмом, учитывая, что в данном примере

На рис. 126 изображена гипербола , построена прямая у= 2-х.Чертеж подтверждает приведенные выкладки: действительно, прямая у = 2-х касается гиперболы в точке(1; 1).

Ответ: у =2- х.Пример 2.К графику функции провести касательную так, чтобы она была параллельна прямой у =4х — 5. Уточним формулировку задачи. Требование «провести касательную» обычно означает «составить уравнение касательной». Это логично, ибо если человек смог составить уравнение касательной, то вряд ли он будет испытывать затруднения с построением на координатной плоскости прямой по ее уравнению.Воспользуемся алгоритмом составления уравнения касательной, учитывая, что в данном примере Но в отличие от предыдущего примера здесь имеется неясность: не указана явно абсцисса точки касания.Начнем рассуждать так. Искомая касательная должна быть параллельна прямой у = 4х-5. Две прямые параллельны тогда и только тогда, когда равны их угловые коэффициенты. Значит, угловой коэффициент касательной должен быть равен угловому коэффициенту заданной прямой: Таким образом, значение а мы можем найти из уравнения f»(а)= 4.Имеем: Из уравнения Значит, имеются две касательные, удовлетворяющие условию задачи: одна в точке с абсциссой 2, другая в точке с абсциссой -2.Теперь можно действовать по алгоритму.

Пример 3. Из точки (0; 1) провести касательную к графику функции Воспользуемся алгоритмом составления уравнения касательной, учитывая, что в данном примере Заметим, что и здесь, как в примере 2, не указана явно абсцисса точки касания. Тем не менее действуем по алгоритму.

По условию касательная проходит через точку (0; 1). Подставив в уравнение (2) значения х = 0, у = 1, получим: Как видите, в этом примере только на четвертом шаге алгоритма нам удалось найти абсциссу точки касания. Подставив значение а =4 в уравнение (2), получим:

На рис. 127 представлена геометрическая иллюстрация рассмотренного примера: построен график функции

В § 32 мы отметили, что для функции у = f(х), имеющей производную в фиксированной точке х, справедливо приближенное равенство:

Для удобства дальнейших рассуждений изменим обозначения: вместо х будем писать а, вместо будем писать х и соответственно вместо будем писать х-а. Тогда написанное выше приближенное равенство примет вид:

А теперь взгляните на рис. 128. К графику функции у = f(х) проведена касательная в точке М (а; f (а)). Отмечена точка х на оси абсцисс близко от а. Ясно, что f(х) — ордината графика функции в указанной точке х. А что такое f(а) + f»(а) (х-а)? Это ордината касательной, соответствующая той же точке х — см. формулу (1). В чем же смысл приближенного равенства (3)? В том, что для вычисления приближенного значения функции берут значение ординаты касательной.

Пример 4. Найти приближенное значение числового выражения 1,02 7 . Речь идет об отыскании значения функции у = х 7 в точке х = 1,02. Воспользуемся формулой (3), учтя, что в данном примере В итоге получаем:Если мы воспользуемся калькулятором, то получим: 1,02 7 = 1,148685667…Как видите, точность приближения вполне приемлема.Ответ: 1,02 7 =1,14.

А.Г. Мордкович Алгебра 10 класс

Календарно-тематическое планирование по математике, видео по математике онлайн , Математика в школе скачать

Содержание урока конспект урока опорный каркас презентация урока акселеративные методы интерактивные технологииПрактика задачи и упражнения самопроверка практикумы, тренинги, кейсы, квесты домашние задания дискуссионные вопросы риторические вопросы от учениковИллюстрации аудио-, видеоклипы и мультимедиа фотографии, картинки графики, таблицы, схемы юмор, анекдоты, приколы, комиксы притчи, поговорки, кроссворды, цитатыДополнения рефераты статьи фишки для любознательных шпаргалки учебники основные и дополнительные словарь терминов прочиеСовершенствование учебников и уроков исправление ошибок в учебнике обновление фрагмента в учебнике элементы новаторства на уроке замена устаревших знаний новымиТолько для учителей идеальные уроки календарный план на год методические рекомендации программы обсужденияИнтегрированные уроки