Главная / Освещение

Определение рангов важности. Сущность теории непараметрической статистики

		События С

	эксперт j = 1
экспертов a ij	эксперт j = 2
	эксперт j = 1
важности а ij	эксперт j = 2
Суммарный ранг важности а i

Среднее значение для суммарных рангов рассматриваемого ряда

Суммарное квадратическое отклонение Sсуммарных событий от среднего значения а есть

называемое коэффициентом конкордации. Величина Wизменяется в пределах от 0 до 1. При W = 0 согласованности совершенно нет, т.е. связь между оценками различных экспертов отсутствует. Наоборот, при W = 1 согласованность мнений экспертов полная.

В том случае, если последовательность (5.2) кроме строгих неравенств имеет равенства, т.е. существует совпадение рангов, то формула для вычисления коэффициента конкордации имеет вид

Когда ранги повторяются, то для получения нормальной ранжировки, имеющей среднее значение ранга, равное

необходимо приписать событиям, имеющим одинаковые ранги, ранг, равный среднему значению мест, которые эти события поделили между собой.

Например, получена следующая ранжировка событий:


Ранги а i

События 2 и 5 поделили между собой второе и третье места. Значит, им приписывается ранг

события 3, 4 и 6 поделили между собой четвертое, пятое, шестое места, и им приписывается ранг

Таким образом, получаем нормальную ранжировку:


Ранги а" i

Пример. Рассмотрим ранжированиеm= 10 событий р = 3 экспертами;N,Q,R. Результаты расчетов представлены в табл. 5.3.

Для крайних значений коэффициента конкордации могут быть высказаны следующие предположения. Если W= 0, то согласованности в оценках нет, поэтому для получения достоверных оценок следует уточнить исходные данные о событиях и (либо) изменить состав группы экспертов. При W = 1 далеко не всегда можно считать полученные оценки объективными, поскольку иногда оказывается, что все члены экспертной группы заранее сговорились, защищая свои общие интересы.

Необходимо, чтобы найденное значение W было больше заданного значения W 3 (W >W 3). Можно принятьW 3 = 0,5, т.е. при W > 0.5 действия экспертов в большей степени согласованы, чем не согласованы. При W < 0,5 полученные оценки нельзя считать достоверными, и поэтому следует повторить опрос заново. Жесткость данного утверждения определяется важностью проводимого исследования и возможностью повторной экспертизы. Практика показывает, что очень часто этим требованием пренебрегают.

Расчет коэффициента W при учете компетентности экспертов приводится в работе .

Коэффициенты корреляции рангов – это менее точные, но более простые по расчету непараметрические показатели для измерения тесноты связи между двумя коррелируемыми признаками. К ним относятся коэффициенты Спирмэна (ρ) и Кендэла (τ), основанные на корреляции не самих значений коррелируемых признаков, а их рангов – порядковых номеров, присваиваемых каждому индивидуальному значению х и у (отдельно) в ранжированном ряду. Оба признака необходимо ранжировать (нумеровать) в одном и том же порядке: от меньших значений к большим и наоборот. Если встречается несколько значений х (или у ), то каждому из них присваивается ранг, равный частному от деления суммы рангов (мест в ряду), приходящихся на эти значения, на число равных значений. Ранги признаков х и у обозначают символами Rx и Ry (иногда Nx и Ny ). Суждение о связи между изменениями значений х и у основано на сравнении поведения рангов по двум признакам параллельно. Если у каждой пары х и у ранги совпадают, это характеризует максимально тесную связь. Если же наблюдается полная противоположность рангов, т.е. в одном ряду ранги возрастают от 1 до n , а в другом – убывают от n до 1, это максимально возможная обратная связь. Подходы для оценки тесноты связи у Спирмэна и Кендэла несколько различаются. Для расчета коэффициента Спирмэна значения признаков х и у нумеруют (отдельно) в порядке возрастания от 1 до n , т.е. им присваивают определенный ранг (Rx и Ry ) – порядковый номер в ранжированном ряду. Затем для каждой пары рангов находят их разность (обозначается как d = Rx – Ry ), и квадраты этой разности суммируют.

где d – разность рангов х и у ;

n – число наблюдаемых пар значений х и у .

Коэффициент ρ может принимать значения от 0 до ±1. Следует иметь в виду, что, поскольку коэффициент Спирмэна учитывает разность только рангов, а не самих значений х и у, он менее точен по сравнению с линейным коэффициентом. Поэто-му его крайние значения (1 или 0) нельзя безоговорочно расцени-вать как свидетельство функциональной связи или полного от-сутствия зависимости между х и у. Во всех других случаях, т.е. когда ρ не принимает крайних зна-чений, он довольно близок к r.

Формула (147) применима строго теоретически только тогда, когда отдельные значения х (и у), а следовательно, и их ранги не повторяются. Для случая повторяющихся (связанных) рангов есть другая, более сложная формула, скорректированная на число по-вторяющихся рангов. Однако опыт показывает, что результаты расчетов по скорректированной формуле для связанных рангов мало отличаются от результатов, полученных по формуле для не-повторяющихся рангов. Поэтому на практике формула (147) ус-пешно применяется как для неповторяющихся, так и для повто-ряющихся рангов.

Коэффициент корреляции рангов Кендэла τ строится несколь-ко по-другому, хотя его расчет также начинается с ранжирования значений признаков х и у. Ранги х (Rx ) располагают строго в порядке возрастания и па-раллельно записывают соответствующее каждому Rx значение Ry . Поскольку Rx записаны строго по возрастанию, то ставится задача определить меру соответствия последовательности Ry «пра-вильному» следованию Rx. При этом для каждого Ry последо-вательно определяют число следующих за ним рангов, превыша-ющих его значение, и число рангов, меньших по значению. Первые («правильное» следование) учитываются как баллы со знаком «+», и их сумма обозначается буквой Р. Вторые («непра-вильное» следование) учитываются как баллы со знаком «–», и их сумма обозначается буквой Q. Очевидно, что максимальное значение Р достигается в том слу-чае, если ранги y (Ry) совпадают с рангами х (Rx) и в каждом ряду представляют ряд натуральных чисел от 1 до п. Тогда после первой пары значений Rx = 1 и Ry = 1 число превышения данных значений рангов составит (n – 1), после второй пары, где Rx = 2 и Ry = 2, соответственно (п – 2) и т.д. Таким образом, если ранги х и у совпадают и число пар рангов равно n , то

Если же последовательность рангов х и у имеет обратную тенденцию по отношению к последовательности рангов х , то Q будет такое же максимальное значение по модулю:

Если же ранги у не совпадают с рангами х , то суммируются все положительные и отрицательные баллы (S=P+Q ); отношение этой суммы S к максимальному значению одного из слагаемых и представляет собой коэффициент корреляции рангов Кендэла τ, т.е.:

. (148)

Формула коэффициента корреляции рангов Кендэла (148) применяется для случаев, когда отдельные значения признака (как х, так и у) не повторяются и, следовательно, их ранги не объе-динены. Если же встречается несколько одинаковых значений х (или у), т.е. ранги повторяются, становятся связанными , коэффици-ент корреляции рангов Кендэла определяется по формуле:

, (149)

где S – фактическая общая сумма баллов при оценке +1 каж-дой пары рангов с одинаковым порядком изменения и –1 каждой пары рангов с обратным порядком изме-нения;

– число баллов, корректирующих (уменьшающих) максимальную сумму баллов за счет повторений (объединений) t рангов в каждом ряду.

Отметим, что случаи следования одинаковых повторяющихся рангов (в любом ряду) оцениваются баллом 0, т.е. они не учиты-ваются при расчете ни со знаком «+», ни со знаком «–».

Преимущества ранговых коэффициентов корреля-ции Спирмэна и Кендэла: они легко вычисляются, с их помощью можно изучать и измерять связь не только между количественны-ми, но и между качественными (описательными) признаками, ранжированными определенным образом. Кроме того, при ис-пользовании ранговых коэффициентов корреляции не требуется знать форму связи изучаемых явлений.

Если число ранжируемых признаков (факторов) больше двух, то для измерения тесноты связи между ними можно использовать предложенный М. Кендэлом и Б. Смитом коэффициент конкордации (множественный коэффициент ранговой корреляции):

, (150)

где S - сумма квадратов отклонений суммы т рангов от их средней величины;

т - число ранжируемых признаков;

п - число ранжируемых единиц (число наблюдений).

Формула (150) применяется для случая, кода ранги по каж-дому признаку не повторяются. Если же есть связанные ран-ги, то коэффициент конкордации рассчитывается с учетом числа таких повторяющихся (связанных) рангов по каждому фактору:

, (151)

где t – число одинаковых рангов по каждому признаку.

Коэффициент конкордации W может принимать значения от 0 до 1. Однако, необходимо проверить его на существенность (значимость) с помощью критерия χ2 при отсутствии связанных рангов по формуле (152), а при их наличии – по формуле (153):

, (152) . (153)

Фактическое значение χ2 сравнивается с табличным, соответ-ствующим принятому уровню значимости α (0,05 или 0,01) и числу степеней свободы v = п – 1. Если χ2факт > χ2табл, то W – существенен (значим).

Коэффициент конкордации особенно часто используется в экспертных оценках, например, для того, чтобы определить сте-пень согласованности мнений экспертов о важности того или иного оцениваемого показателя или составить рейтинг отдельных единиц по какому-либо признаку. В формуле (150) в этих случаях т означает число экспертов, а n - число ранжируемых единиц (или признаков).

Достаточно хорошо аппроксимирует Р. с. Т, и разность пренебрежимо мала, когда . При справедливости гипотезы H 0 , согласно к-рой компоненты Х 1 , ... , Х n случайного вектора Xсуть независимые случайные величины, проекция Р. с. Топределяется по формуле

где (см. ).

Существует внутренняя связь между Р. с. и . Как показано в , при справедливости гипотезы H 0 проекция коэффициента корреляции Кендалла в семейство линейных Р. с. с точностью до постоянного множителя совпадает с коэффициентом ранговой корреляции Спирмена , а именно:

Из этого равенства следует, что коэффициент корреляции соrr между и равен

т. е. при больших пР. с. и асимптотически эквивалентны (см. ).

Лит. : Г а е к Я., Ш и д а к З., Теория ранговых критериев, пер. с англ., М., 1971; К е n d a l l M. G., Rank correlation methods, 4ed., L., 1970. М. С. Никулин.

Математическая энциклопедия. - М.: Советская энциклопедия . И. М. Виноградов . 1977-1985 .

Смотреть что такое "РАНГОВАЯ СТАТИСТИКА" в других словарях:

ранговая статистика - — [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом EN rank statistics … Справочник технического переводчика

У этого термина существуют и другие значения, см. Статистика (значения). Статистика (в узком смысле) это измеримая числовая функция от выборки, не зависящая от неизвестных параметров распределения. В широком смысле термин (математическая)… … Википедия

- (statistics) 1. Совокупность данных и математических методов, используемых для изучения связей между различными переменными. Она включает такие методы, как линейная регрессия (linear regression) и ранговая корреляция. 2. Значения, использующиеся… … Экономический словарь

СТАТИСТИКА - 1. Вид деятельности, направленной на получение, обработку и анализ информации, характеризующей количественные закономерности жизни об ва во всем ее многообразии, в неразрывной связи с ее качественным содержанием. В более узком смысле слова… … Российская социологическая энциклопедия

- (non parametric statistics) Статистические технические приемы, которые не допускают особенных функциональных форм для отношений между переменными. Ранговая корреляция двух переменных является тому примером. Использование подобных технических… … Экономический словарь - К. м., получившие свое назв. благодаря тому, что основываются на «со отношении» («co relation») переменных, представляют собой статистические методы, начало к рым было положено в работах Карла Пирсона примерно в конце XIX в. Они тесно связаны с… … Психологическая энциклопедия

Разработчик Digital Illusions CE Издатель … Википедия

Карл Пирсон Karl (Carl) Pearson Дата рождения … Википедия

Коэффициент тесноты связи между признаками, рассмотренный в предыдущем разделе, можно применять, если изучаемые признаки являются количественными. При этом используется вычисление основных параметров распределения (средних величин, дисперсий), т.е. параметрический метод.

В статистической практике изучения общественно-экономических явлений и процессов приходится сталкиваться с задачами измерения связи между качественными признаками, к которым параметрические методы анализа в их обычном виде неприменимы. В этом случае используют так называемые непараметрические методы.

В анализе социально-экономических явлений широко используются ранговые коэффициенты корреляции (коэффициенты корреляции рангов), когда коррелируют не непосредственные значения х и у, а их ранги, т.е. номера их мест, занимаемых в каждом ряду значений по возрастанию или убыванию. К таким непараметрическим коэффициентам относятся коэффициенты рангов Спирмена и Кендалла.

Если п вариантов ряда расположены в соответствии с возрастанием или убыванием признака х, то говорят, что объекты ранжированы по этому признаку. Ранг для х,- указывает место, которое занимает i-e значение признака среди других п значений признака х (/ = 1,2,___, п).

Например, при исследовании рынка можно задаться целью выяснения предпочтений потребителей при выборе товара (при покупке акций, мороженого, автомобиля и т.п.) таким образом, чтобы они распределили товар в порядке возрастания (или убывания) своих потребительских предпочтений. Если имеется два набора ранжированных данных, то можно установить степень линейной зависимости между ними.

Пример 6.7. Предположим, имеется 5 продуктов (табл. 6.7), которые ранжированы по порядку предпочтений от 1 до 5 в соответствии с двумя характеристиками Aw В.

Исходные ранжировки

Таблица 6 .7

Необходимо исследовать тесноту статистической связи между характеристиками.

Решение. Использование для определения интенсивности связи между признаками коэффициента Пирсона будет неверным, так как этот коэффициент применяется для признаков, измеряемых количественно. Так, например, при определении взаимосвязи между ростом и весом мы измеряем рост в сантиметрах, а вес в килограммах, при этом есть возможность точно определить на шкале измерений разность значений этих признаков для любого человека (иначе - расстояние между ними на шкале измерений). Возьмем признак, измеренный в ранговой шкале, - экзаменационная оценка. Значит ли, что у получившего двойку студента знаний в два раза меньше, чем у того, кто получил четверку? Или двое студентов, получивших тройки, имеют абсолютно одинаковый уровень знаний? Ответ - нет, преподаватель упорядочивает их уровень знаний в определенной последовательности, в соответствии с критериями оценки знаний по конкретному предмету, но расстояние между значениями признаков на такой шкале не является строго фиксированным.

Для определения наличия взаимосвязи между ранговыми оценками используется коэффициент ранговой корреляции Спирмена. Его расчет основан на различиях между рангами.

Обозначим разность рангов d = ранг А ~ ранг В.

Коэффициент Спирмена

где п - число пар ранжированных наблюдений.

В примере имеем пять пар рангов, следовательно, п- 5. Сумма ct равна

Тогда коэффициент Спирмена

Коэффициент Спирмена изменяется в интервале [-1; 1] и интерпретируется так же, как и коэффициент Пирсона. Отличие в том, что он вычисляется для ранжированных данных.

Значение 0,6 позволяет сделать вывод о заметной линейной связи между двумя характеристиками товаров.

Значимость коэффициента Спирмена проверяется на основе t критерия Стьюдента по формуле

Значение коэффициента считается существенным, если t paсч > > 6фит;а (и - 2) для заданного уровня значимости а.

Коэффициент корреляции рангов (при условии, что ранги не повторяются) может быть рассчитан и по формуле, предложенной английским статистиком М. Кендаллом:

где S - фактическая разность рангов; ~ п (п - l) - максимальная сумма рангов.

Этот коэффициент изменяется в интервале от [-1; 1] и интерпретируется так же, как и коэффициент Пирсона, но дает более строгую

оценку связи, чем коэффициент Спирмена, причем р = - т. Это соотношение выполняется при большом числе наблюдений (п > 30), и слабых либо умеренно тесных связях.

При расчете коэффициента Кендалла соблюдается следующая последовательность действий:

1. Значения х ранжируются в порядке возрастания.
2. Значения у располагаются в порядке, соответствующем значениям х.
3. Для каждого ранга у определяется число следующих за ним значений рангов, превышающих его величину. Результат записывается в столбец «+».
4. Для каждого ранга у определяется число следующих за ним меньших значений рангов. Результат записывается в столбец «-».
5. Находится сумма в столбце «+» и обозначается Р, в столбце «-» и обозначается Q. Определяется S = P- Q.

Значимость коэффициента корреляции рангов Кендалла проверяется по формуле

где щ_ а/2 (п - 2) - квантиль, определяемый по таблице нормального распределения для выбранного уровня значимости а и заданного п.

Пример 6.8. Рассчитаем коэффициент Кендалла на основании данных примера 6.7.

Решение. Проведем необходимые расчеты в табл. 6.8.

Действительно, если полученное значение т умножить на 1,5, то получим 0,6 - значение коэффициента Спирмена, рассчитанное в примере 6.7.

Расчетная таблица

Рассмотрим корреляцию альтернативных признаков, т.е.признаков, принимающих только два возможных значения. Исследования их корреляции основано на показателях, построенных на четырехклеточных таблицах, в которые сводится число единиц для заданных значений признаков:

Решение. Для измерения тесноты взаимосвязи признаков производится расчет коэффициента контингенции по формуле

Коэффициент контингенции принимает значения на интервале [-1; 1 ]. Интерпретация аналогична коэффициенту корреляции. Мы получили слабую отрицательную связь.

Другой метод измерения связи основан на расчете коэффициента ассоциации:

„ л 30x5-20x15 л „

Получим: Q =-= -0,33

Знак «минус» перед коэффициентом указывает на то, что чем больше студентов было привито от гриппа, тем ниже заболеваемость.

Коэффициент контингенции всегда бывает меньше коэффициента ассоциации и дает более корректную оценку тесноты связи.

Для оценки тесноты связи между признаками, принимающими любое число вариантов значений (категориальные, номинальные признаки), применяется коэффициент взаимной сопряженности Пирсона. Основой изучения связи между категориальными признаками служит таблица сопряженности - двумерное распределение единиц совокупности по признакам. Вся информация о наличии или отсутствии связи содержится в совместных частотах сочетаний признаков.

Информация для оценки этой связи группируется в виде таблицы (например, для трех значений первого признака и двух - второго), табл. 6.10.

Таблица 6.10

Пример таблицы сопряженности

Признак		Итого


	Ъгпц	ЪЪгпц

Обозначения: ту - частоты взаимного сочетания двух атрибутивных признаков; п = YLmy - число наблюдений.

Коэффициент взаимной сопряженности Пирсона определяется по формуле

где ср - показатель средней квадратической сопряженности:

Коэффициент взаимной сопряженности принимает значения в интервале и интерпретируется подобно коэффициенту парной линейной корреляции Пирсона.

Пример 6.10. Для изучения влияния условий труда на взаимоотношения в коллективе было проведено выборочное обследование 250 работников предприятия, ответы которых распределились, как представлено в табл. 6.11.

Таблица 6.11

Исходные данные об условиях труда и взаимоотношениях в коллективе

Требуется охарактеризовать связь между исследуемыми показателями с помощью коэффициента взаимной сопряженности Пирсона.

Решение.

Полученное значение коэффициента сопряженности свидетельствует, что связь между условиями труда и взаимоотношениями в коллективе умеренная.

При изучении общественного здоровья и здравоохранения в научных и практических целях исследователю часто приходится проводить статистический анализ связей между факторными и результативными признаками статистический совокупности (причинно-следственная связь) или определение зависимости параллельных изменений нескольких признаков этой совокупности от какой либо третьей величины (от общей их причины). Необходимо уметь изучать особенности этой связи, определять ее размеры и направление, а также оценивать ее достоверность. Для этого используются методы корреляции.

Виды проявления количественных связей между признаками
- функциональная связь
- корреляционная связь
Определения функциональной и корреляционной связи
Функциональная связь - такой вид соотношения между двумя признаками, когда каждому значению одного из них соответствует строго определенное значение другого (площадь круга зависит от радиуса круга и т.д.). Функциональная связь характерна для физико-математических процессов.
Корреляционная связь - такая связь, при которой каждому определенному значению одного признака соответствует несколько значений другого взаимосвязанного с ним признака (связь между ростом и массой тела человека; связь между температурой тела и частотой пульса и др.). Корреляционная связь характерна для медико-биологических процессов.
Практическое значение установления корреляционной связи . Выявление причинно-следственной между факторными и результативными признаками (при оценке физического развития, для определения связи между условиями труда, быта и состоянием здоровья, при определении зависимости частоты случаев болезни от возраста, стажа, наличия производственных вредностей и др.)
Зависимость параллельных изменений нескольких признаков от какой-то третьей величины. Например, под воздействием высокой температуры в цехе происходят изменения кровяного давления, вязкости крови, частоты пульса и др.
Величина, характеризующая направление и силу связи между признаками . Коэффициент корреляции, который одним числом дает представление о направлении и силе связи между признаками (явлениями), пределы его колебаний от 0 до ± 1
Способы представления корреляционной связи
- график (диаграмма рассеяния)
- коэффициент корреляции
Направление корреляционной связи
- прямая
- oбратная
Сила корреляционной связи
- сильная: ±0,7 до ±1
- средняя: ±0,3 до ±0,699
- слабая: 0 до ±0,299
Методы определения коэффициента корреляции и формулы
- метод квадратов (метод Пирсона)
- ранговый метод (метод Спирмена)
Методические требования к использованию коэффициента корреляции
- измерение связи возможно только в качественно однородных совокупностях (например, измерение связи между ростом и весом в совокупностях, однородных по полу и возрасту)
- расчет может производиться с использованием абсолютных или производных величин
- для вычисления коэффициента корреляции используются не сгруппированные вариационные ряды (это требование применяется только при вычислении коэффициента корреляции по методу квадратов)
- число наблюдений не менее 30
Рекомендации по применению метода ранговой корреляции (метод Спирмена)
- когда нет необходимости в точном установлении силы связи, а достаточно ориентировочных данных
- когда признаки представлены не только количественными, но и атрибутивными значениями
- когда ряды распределения признаков имеют открытые варианты (например, стаж работы до 1 года и др.)
Рекомендации к применению метода квадратов (метод Пирсона)
- когда требуется точное установление силы связи между признаками
- когда признаки имеют только количественное выражение
Методика и порядок вычисления коэффициента корреляции
1) Метод квадратов
2) Ранговый метод
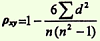
Схема оценки корреляционной связи по коэффициенту корреляции
Вычисление ошибки коэффициента корреляции
Оценка достоверности коэффициента корреляции,полученного методом ранговой корреляции и методом квадратов
Способ 1
Достоверность определяется по формуле:
Критерий t оценивается по таблице значений t с учетом числа степеней свободы (n - 2), где n - число парных вариант. Критерий t должен быть равен или больше табличного, соответствующего вероятности р ≥99%.
Способ 2
Достоверность оценивается по специальной таблице стандартных коэффициентов корреляции. При этом достоверным считается такой коэффициент корреляции, когда при определенном числе степеней свободы (n - 2), он равен или более табличного, соответствующего степени безошибочного прогноза р ≥95%.

на применение метода квадратов

Задание: вычислить коэффициент корреляции, определить направление и силу связи между количеством кальция в воде и жесткостью воды, если известны следующие данные (табл. 1). Оценить достоверность связи. Сделать вывод.

Таблица 1

Обоснование выбора метода. Для решения задачи выбран метод квадратов (Пирсона), т.к. каждый из признаков (жесткость воды и количество кальция) имеет числовое выражение; нет открытых вариант.

Решение .
Последовательность расчетов изложена в тексте, результаты представлены в таблице. Построив ряды из парных сопоставляемых признаков, обозначить их через х (жесткость воды в градусах) и через у (количество кальция в воде в мг/л).

Жесткость воды (в градусах)	Количество кальция в воде (в мг/л)	d х	d у	d х х d у	d x 2	d y 2
4 8 11 27 34 37	28 56 77 191 241 262	-16 -12 -9 +7 +14 +16	-114 -86 -66 +48 +98 +120	1824 1032 594 336 1372 1920	256 144 81 49 196 256	12996 7396 4356 2304 9604 14400
М х =Σ х / n	М у =Σ у / n			Σ d х x d у =7078	Σ d х 2 =982	Σ d y 2 =51056
М х =120/6=20	М y =852/6=142

Определить средние величины M x ряду вариант "х" и М у в ряду вариант "у" по формулам:
М х = Σх/n (графа 1) и
М у = Σу/n (графа 2)
Найти отклонение (d х и d у) каждой варианты от величины вычисленной средней в ряду "x" и в ряду "у"
d х = х - М х (графа 3) и d y = у - М у (графа4).
Найти произведение отклонений d x х d y и суммировать их: Σ d х х d у (графа 5)
Каждое отклонение d x и d у возвести в квадрат и суммировать их значения по ряду "х" и по ряду "у": Σ d x 2 = 982 (графа 6) и Σ d y 2 = 51056 (графа 7).
Определить произведение Σ d x 2 х Σ d y 2 и из этого произведения извлечь квадратный корень
Полученные величины Σ (d x x d y) и √(Σd x 2 x Σd y 2) подставляем в формулу расчета коэффициента корреляции:

Определить достоверность коэффициента корреляции:
1-й способ. Найти ошибку коэффициента корреляции (mr xy) и критерий t по формулам:

Критерий t = 14,1, что соответствует вероятности безошибочного прогноза р > 99,9%.

2-й способ. Достоверность коэффициента корреляции оценивается по таблице "Стандартные коэффициенты корреляции" (см. приложение 1). При числе степеней свободы (n - 2)=6 - 2=4, наш расчетный коэффициент корреляции r xу = + 0,99 больше табличного (r табл = + 0,917 при р = 99%).

Вывод. Чем больше кальция в воде, тем она более жесткая (связь прямая, сильная и достоверная : r ху = + 0,99, р > 99,9%).

на применение рангового метода

Задание: методом рангов установить направление и силу связи между стажем работы в годах и частотой травм, если получены следующие данные:

Обоснование выбора метода: для решения задачи может быть выбран только метод ранговой корреляции, т.к. первый ряд признака "стаж работы в годах" имеет открытые варианты (стаж работы до 1 года и 7 и более лет), что не позволяет использовать для установления связи между сопоставляемыми признаками более точный метод - метод квадратов.

Решение . Последовательность расчетов изложена в тексте, результаты представлены в табл. 2.

Таблица 2

Стаж работы в годах	Число травм	Порядковые номера (ранги)		Разность рангов	Квадрат разности рангов
Стаж работы в годах	Число травм	X	Y	d(х-у)	d 2
До 1 года	24	1	5	-4	16
1-2	16	2	4	-2	4
3-4	12	3	2,5	+0,5	0,25
5-6	12	4	2,5	+1,5	2,25
7 и более	6	5	1	+4	16
					Σ d 2 = 38,5

Стандартные коэффициенты корреляции, которые считаются достоверными (по Л.С. Каминскому)

Число степеней свободы - 2	Уровень вероятности р (%)
Число степеней свободы - 2	95%	98%	99%
1	0,997	0,999	0,999
2	0,950	0,980	0,990
3	0,878	0,934	0,959
4	0,811	0,882	0,917
5	0,754	0,833	0,874
6	0,707	0,789	0,834
7	0,666	0,750	0,798
8	0,632	0,716	0,765
9	0,602	0,885	0,735
10	0,576	0,858	0,708
11	0,553	0,634	0,684
12	0,532	0,612	0,661
13	0,514	0,592	0,641
14	0,497	0,574	0,623
15	0,482	0,558	0,606
16	0,468	0,542	0,590
17	0,456	0,528	0,575
18	0,444	0,516	0,561
19	0,433	0,503	0,549
20	0,423	0,492	0,537
25	0,381	0,445	0,487
30	0,349	0,409	0,449

Власов В.В. Эпидемиология. - М.: ГЭОТАР-МЕД, 2004. - 464 с.
Лисицын Ю.П. Общественное здоровье и здравоохранение. Учебник для вузов. - М.: ГЭОТАР-МЕД, 2007. - 512 с.
Медик В.А., Юрьев В.К. Курс лекций по общественному здоровью и здравоохранению: Часть 1. Общественное здоровье. - М.: Медицина, 2003. - 368 с.
Миняев В.А., Вишняков Н.И. и др. Социальная медицина и организация здравоохранения (Руководство в 2 томах). - СПб, 1998. -528 с.
Кучеренко В.З., Агарков Н.М. и др.Социальная гигиена и организация здравоохранения (Учебное пособие) - Москва, 2000. - 432 с.
С. Гланц. Медико-биологическая статистика. Пер с англ. - М., Практика, 1998. - 459 с.