Решение уравнения в частных производных смешанного типа. Дифференциальные уравнения для «чайников». Примеры решения

Пусть X 1 , X 2 , …, X n — заданные функции переменных x 1 , x 2 , …, x n.

Чтобы решить линейное однородное уравнение в частных производных первого порядка: необходимо решить систему обыкновенных дифференциальных уравнений (уравнение характеристик):: Далее нужно представить решение в виде:φ 1 (x 1 , x 2 , …, x n ) = C 1,φ 2 (x 1 , x 2 , …, x n ) = C 2, ………………φ n-1 (x 1 , x 2 , …, x n ) = C n-1, где C k — постоянные. После чего сразу получаем общее решение:, где F — произвольная функция от n — 1 аргументов.

Если нужно получить частное решение с определенными граничными условиями, то необходимо подставить значения переменных из граничных условий в общее решение и найти вид функции F.

Линейные неоднородные уравнения в частных производных первого порядка

Пусть X 1 , X 2 , …, X n+1 — заданные функции от переменных x 1 , x 2 , …, x n и z.

Чтобы решить линейное неоднородное уравнение в частных производных первого порядка:, необходимо решить уравнение характеристик:. Решение этой системы нужно представить в следующем виде:φ 1 (x 1 , x 2 , …, x n , z ) = C 1,φ 2 (x 1 , x 2 , …, x n , z ) = C 2, ………………φ n (x 1 , x 2 , …, x n , z ) = C n. После чего сразу получаем общий интеграл в неявном виде: где F — произвольная функция. Также общий интеграл можно представить в различных вариантах, например:φ 1 = F(φ 2 , φ 3 , …, φ n ),φ 2 = F(φ 1 , φ 3 , …, φ n ), и т. д.

Примеры решений линейных уравнений в частных производных первого порядка

Однородное уравнение

Условие задачи

Найти общее решение линейного однородного уравнения в частных производных первого порядка и решить задачу Коши с указанным граничным условием:, при .

Решение

Это линейное однородное уравнение в частных производных первого порядка. Составляем уравнение характеристик:

Это уравнение характеристик содержит три уравнения:;;. Нам нужно выбрать и решить любые два из них. Тогда третье будет выполнено автоматически.

Выбираем и решаем первое уравнение: Здесь переменные уже разделены, интегрируем: Интегралы табличные, Потенцируем: Отсюда

Или: интегрирующего множителя . Умножим на x -1 и преобразуем: Интегрируем: Подставим полученное ранее выражение C 1 = x y 2:

Общее решение исходного уравнения в частных производных имеет вид: где F — произвольная функция от двух аргументов F(φ 1 , φ 2). Найдем ее вид из граничного условия при .

Рассматриваем решение на границе. Положим x y = -1: Отсюда На границе.

F(φ 1 , φ 2 ) = φ 1 φ 2. Такой же вид она имеет и во всей области Подставляя;, получаем частное решение исходного уравнения в частных производных с заданным граничным условием:

Ответ

Общее решение: где F — произвольная функция от двух аргументов F(φ 1 , φ 2 ).

Частное решение:

Неоднородное уравнение

Условие задачи

Найти поверхность, удовлетворяющую данному уравнению, и проходящую через данную окружность x + y + z = 0, x 2 + y 2 + z 2 = a 2.

Решение

Это линейное неоднородное уравнение в частных производных первого порядка. Составляем уравнение характеристик:

Оно содержит три уравнения:;;. Нам нужно выбрать и решить любые два из них. Тогда третье удовлетворится автоматически. Выбираем первое и второе уравнения.

Решаем уравнение: Умножаем на 2 z и интегрируем: Интегралы табличные, Потенцируем: Отсюдаx = C 1 y

Подставим во второе уравнение: Или: Замечаем, что , тогда Это линейное уравнение. Решаем с помощью интегрирующего множителя . Разделим на y 2 и преобразуем: Интегрируем: Подставим полученное ранее выражение и преобразуем:

Итак, мы нашли два интеграла уравнения характеристик:

Для удобства дальнейших вычислений заметим, что функция от постоянной также является постоянной. Поэтому запишем интегралы в виде:

Общий интеграл исходного уравнения в частных производных имеет вид:F(φ 1 , φ 2) = 0 Но, поскольку F — произвольная функция от двух аргументов, то общий интеграл можно записать также в виде:φ 1 = F(φ 2), где F — произвольная функция от одного аргумента.

Найдем вид этой функции, рассматривая решение на границе. На границе, x 2 + y 2 + z 2 = a 2, . Из уравнения x + y + z = 0, z = -(x + y). Подставим в x 2 + y 2 + z 2 = a 2 и преобразуем:x 2 + y 2 + (x + y) 2 = a 2x 2 + y 2 + x 2 + 2xy + y 2 = a 22x 2 + 2xy + 2y 2 = a 2 Разделив на y 2, имеем Итак, мы нашли, что на границе:. Подставим в выражение общего интеграла:φ 1 = F(φ 2). Сделаем подстановку:.

Итак, мы нашли, что на границе функция F имеет вид:. Такой же вид она имеет и во всей области, тогда. Подставляем выражения для φ 1 и φ 2:. Умножим на a 2 y 2.

Часто одно лишь упоминание дифференциальных уравнений вызывает у студентов неприятное чувство. Почему так происходит? Чаще всего потому, что при изучении основ материала возникает пробел в знаниях, из-за которого дальнейшее изучение дифуров становиться просто пыткой. Ничего не понятно, что делать, как решать, с чего начать?

Однако мы постараемся вам показать, что дифуры – это не так сложно, как кажется.

Основные понятия теории дифференциальных уравнений

Со школы нам известны простейшие уравнения, в которых нужно найти неизвестную x. По сути дифференциальные уравнения лишь чуточку отличаются от них – вместо переменной х в них нужно найти функцию y(х), которая обратит уравнение в тождество.

Дифференциальные уравнения имеют огромное прикладное значение. Это не абстрактная математика, которая не имеет отношения к окружающему нас миру. С помощью дифференциальных уравнений описываются многие реальные природные процессы. Например, колебания струны, движение гармонического осциллятора, посредством дифференциальных уравнений в задачах механики находят скорость и ускорение тела. Также ДУ находят широкое применение в биологии, химии, экономике и многих других науках.

Дифференциальное уравнение (ДУ) – это уравнение, содержащее производные функции y(х), саму функцию, независимые переменные и иные параметры в различных комбинациях.

Существует множество видов дифференциальных уравнений: обыкновенные дифференциальные уравнения, линейные и нелинейные, однородные и неоднородные, дифференциальные уравнения первого и высших порядков, дифуры в частных производных и так далее.

Решением дифференциального уравнения является функция, которая обращает его в тождество. Существуют общие и частные решения ДУ.

Общим решением ДУ является общее множество решений, обращающих уравнение в тождество. Частным решением дифференциального уравнения называется решение, удовлетворяющее дополнительным условиям, заданным изначально.

Порядок дифференциального уравнения определяется наивысшим порядком производных, входящих в него.

Обыкновенные дифференциальные уравнения

Обыкновенные дифференциальные уравнения – это уравнения, содержащие одну независимую переменную.

Рассмотрим простейшее обыкновенное дифференциальное уравнение первого порядка. Оно имеет вид:

Решить такое уравнение можно, просто проинтегрировав его правую часть.

Примеры таких уравнений:

Уравнения с разделяющимися переменными

В общем виде этот тип уравнений выглядит так:

Приведем пример:

Решая такое уравнение, нужно разделить переменные, приведя его к виду:

После этого останется проинтегрировать обе части и получить решение.

Линейные дифференциальные уравнения первого порядка

Такие уравнения имеют вид:

Здесь p(x) и q(x) – некоторые функции независимой переменной, а y=y(x) – искомая функция. Приведем пример такого уравнения:

Решая такое уравнение, чаще всего используют метод вариации произвольной постоянной либо представляют искомую функцию в виде произведения двух других функций y(x)=u(x)v(x).

Для решения таких уравнений необходима определенная подготовка и взять их “с наскока” будет довольно сложно.

Пример решения ДУ с разделяющимися переменными

Вот мы и рассмотрели простейшие типы ДУ. Теперь разберем решение одного из них. Пусть это будет уравнение с разделяющимися переменными.

Сначала перепишем производную в более привычном виде:

Затем разделим переменные, то есть в одной части уравнения соберем все «игреки», а в другой – «иксы»:

Теперь осталось проинтегрировать обе части:

Интегрируем и получаем общее решение данного уравнения:

Конечно, решение дифференциальных уравнений – своего рода искусство. Нужно уметь понимать, к какому типу относится уравнение, а также научиться видеть, какие преобразования нужно с ним совершить, чтобы привести к тому или иному виду, не говоря уже просто об умении дифференцировать и интегрировать. И чтобы преуспеть в решении ДУ, нужна практика (как и во всем). А если у Вас в данный момент нет времени разбираться с тем, как решаются дифференциальные уравнения или задача Коши встала как кость в горле или вы не знаете, обратитесь к нашим авторам. В сжатые сроки мы предоставим Вам готовое и подробное решение, разобраться в подробностях которого Вы сможете в любое удобное для Вас время. А пока предлагаем посмотреть видео на тему «Как решать дифференциальные уравнения»:

Дифференциальное уравнение в частных производных (частные случаи также известны как уравнения математической физики, УМФ) — дифференциальное уравнение , содержащее неизвестные функции нескольких переменных и их частные производные .

Энциклопедичный YouTube

1/5

✪ Дифференциальные уравнения в частных производных. Привидение к каноническому виду.

✪ Уравнения математической физики. Шаньков В.В. Весенний семестр. Лекция №1

✪ Методы математической физики. Тихонов Николай Андреевич (Лекция 10)

✪ 8 Дифференциальные уравнения в частных производных Mathcad

✪ Дифференциальные уравнения 1. Вязкое торможение

Субтитры

Введение

Рассмотрим сравнительно простое уравнение в частных производных:

∂ ∂ y u (x , y) = 0 . {displaystyle {frac {partial }{partial y}}u(x,y)=0,.}

Задачи доказательств существования и нахождения решений систем нелинейных дифференциальных уравнений в частных производныхрешаются с использованием теории гладких многообразий , дифференциальнойгеометрии , коммутативной и гомологической алгебры . Эти методы применяются в физике при изучении лагранжева и гамильтонова формализма, исследовании высших симметрий изаконов сохранения .

Классификация

Размерность

Равна количеству независимых переменных. Должна быть не меньше 2 (при 1 получается обыкновенное дифференциальное уравнение).

Линейность

Есть линейные и нелинейные уравнения. Линейное уравнение представимо в виде линейной комбинации производных от неизвестных функций. Коэффициенты при этом могут быть либо постоянными , либо известными функциями.

Линейные уравнения хорошо исследованы, за решение отдельных видов нелинейных уравнений назначены миллионные премии (задачи тысячелетия).

Однородность

Уравнение является неоднородным, если есть слагаемое, не зависящее от неизвестных функций.

Порядок

Порядок уравнения определяется максимальным порядком производной. Имеют значение порядки по всем переменным.

Классификация линейных уравнений второго порядка

Линейные уравнения второго порядка в частных производных подразделяют на параболические , эллиптические и гиперболические .

Две независимые переменные

Линейное уравнение второго порядка, содержащее две независимые переменные, имеет вид:

A ∂ 2 u ∂ x 2 + 2 B ∂ 2 u ∂ x ∂ y + C ∂ 2 u ∂ y 2 + . . . = 0 , {displaystyle A{frac {partial ^{2}u}{partial x^{2}}}+2B{frac {partial ^{2}u}{partial xpartial y}}+C{frac {partial ^{2}u}{partial y^{2}}}+…=0,}

где A, B, C — коэффициенты, зависящие от переменных x и y, а многоточие означает члены, зависящие от x, y, u и частных производных первого порядка: ∂ u / ∂ x {displaystyle {partial u}/{partial x}} и ∂ u / ∂ y {displaystyle {partial u}/{partial y}}. Это уравнение похоже на уравнение конического сечения :

A x 2 + 2 B x y + C y 2 + ⋯ = 0. {displaystyle Ax^{2}+2Bxy+Cy^{2}+cdots =0.}

Так же, как конические сечения разделяются на эллипсы , параболы и гиперболы , в зависимости от знака дискриминанта D = B 2 − A C {displaystyle D=B^{2}-AC}, классифицируются уравнения второго порядка в заданной точке:

В случае, когда все коэффициенты A, B, C — постоянные, уравнение имеет один и тот же тип во всех точках плоскости переменных x и y. В случае, если коэффициенты A, B, C непрерывно зависят от x и y, множество точек, в которых данное уравнение относится к гиперболическому (эллиптическому), типу образует на плоскости открытую область, называемую гиперболической (эллиптической), а множество точек, в которых уравнение относится к параболическому типу, замкнуто. Уравнение называется смешанным (смешанного типа), если в некоторых точках плоскости оно гиперболическое, а в некоторых — эллиптическое. В этом случае параболические точки, как правило, образуют линию, называемую линией смены типа или линией вырождения.

Более двух независимых переменных

В общем случае, когда уравнение второго порядка зависит от многих независимых переменных:

∑ i = 1 n ∑ j = 1 n a i j (x 1 , ⋯ , x n) ∂ 2 u ∂ x i ∂ x j + F (x 1 , ⋯ , x n , u , ∂ u ∂ x 1 , ⋯ , ∂ u ∂ x n) = 0 , {displaystyle sum _{i=1}^{n}sum _{j=1}^{n}a_{ij}(x_{1},cdots ,x_{n}){frac {partial ^{2}u}{partial x_{i}partial x_{j}}}+Fleft(x_{1},cdots ,x_{n},u,{frac {partial u}{partial x_{1}}},cdots ,{frac {partial u}{partial x_{n}}}right)=0,}

оно может быть классифицированов заданной точке M 0 (x 1 0 , ⋯ , x n 0) {displaystyle M_{0}(x_{1}^{0},cdots ,x_{n}^{0})} по аналогии с соответствующей квадратичной формой:

∑ i = 1 n ∑ j = 1 n a i j (x 1 0 , ⋯ , x n 0) t i t j . {displaystyle sum _{i=1}^{n}sum _{j=1}^{n}a_{ij}(x_{1}^{0},cdots ,x_{n}^{0})t_{i}t_{j}.}

Невырожденным линейным преобразованием

s i = ∑ j = 1 n A i j t j , i = 1 , 2 ⋯ n , det ‖ A i j ‖ ≠ 0 {displaystyle s_{i}=sum _{j=1}^{n}A_{ij}t_{j},i=1,2cdots n,det left|A_{ij}right|neq 0}

квадратичная форма всегда может быть приведена к каноническому виду:

∑ i = 1 n λ i s i 2 . {displaystyle sum _{i=1}^{n}lambda _{i}s_{i}^{2}.}

При этом согласно теореме инерции число положительных, отрицательных и равных нулю коэффициентов λ i {displaystyle lambda _{i}} в каноническом виде квадратичной формы является инвариантом и не зависит от линейного преобразования. На основе этого и производится классификация (в точке M 0 {displaystyle M_{0}}) рассматриваемого уравнения:

В случае многих независимых переменных может быть проведена и более подробная классификация (необходимость которой в случае двух независимых переменных не возникает):

1. Гиперболический тип
   1. Нормальный гиперболический тип, если один коэффициент одного знака, а остальные другого.
   2. Ультрагиперболический тип, если коэффициентов как одного знака так и другого более чем один.
2. Параболический тип может быть дополнительно классифицирован на:
   1. Эллиптически-параболический тип, если только один коэффициент равен нулю, а остальные имеют один знак.
   2. Гиперболически-параболический тип, если только один коэффициент равен нулю, а остальные имеют различные знаки. Аналогично гиперболическому типу он может быть разделён на:
      1. Нормальный гиперболически-параболический тип
      2. Ультрагиперболически-параболический тип
   3. Ультрапараболический тип, если более чем один коэффициент равен нулю. Здесь также возможна дальнейшая классификация в зависимости от знаков не равных нулю коэффициентов.

Существование и единственность решения

Хотя ответ на вопрос о существовании и единственности решения обыкновенного дифференциального уравнения имеет вполне исчерпывающий ответ (теорема Пикара — Линделёфа), для уравнения в частных производных однозначного ответа на этот вопрос нет.Существует общая теорема (теорема Коши - Ковалевской), которая утверждает, что задача Коши для любого уравнения в частных производных, аналитического относительно неизвестных функций и их производных имеет единственное аналитическое решение . Тем не менее, существуют примеры линейных уравнений в частных производных, коэффициенты которых имеют производные всех порядков и не имеющих решения (Леви , ). Даже если решение существует и единственно, оно может иметь нежелательные свойства.

Рассмотрим последовательность задач Коши (зависящую от n) для уравнения Лапласа :

∂ 2 u ∂ x 2 + ∂ 2 u ∂ y 2 = 0 , {displaystyle {frac {partial ^{2}u}{partial x^{2}}}+{frac {partial ^{2}u}{partial y^{2}}}=0,} u (x , 0) = 0 , {displaystyle u(x,0)=0,} ∂ u ∂ y (x , 0) = sin ⁡ n x n , {displaystyle {frac {partial u}{partial y}}(x,0)={frac {sin nx}{n}},}

где n — целое. Производная от функции u по переменной y равномерно стремится к 0 по x при возрастании n , однако решением уравнения является

u (x , y) = (s h n y) (sin ⁡ n x) n 2 . {displaystyle u(x,y)={frac {(mathrm {sh} ,ny)(sin nx)}{n^{2}}}.}

Решение стремится к бесконечности, если nx не кратно π {displaystyle pi } для любого ненулевого значения y. Задача Коши для уравнения Лапласа называется плохо поставленной или некорректной , так как нет непрерывной зависимости решения от начальных данных.

Для систем нелинейных дифференциальных уравнений в частных производных доказательства существования решений и поиск многообразий всех решений проводятся с использованием теории гладких многообразий , дифференциальной геометрии , коммутативной и гомологической алгебры . Эти методы применяются в физике при изучении лагранжева и гамильтонова формализма, исследовании высших симметрий и законов сохранения .

Примеры

Одномерное уравнение теплопроводности

Уравнение, описывающее распространение тепла в однородном стержне относится к параболическому типу и имеет вид

∂ u ∂ t = α ∂ 2 u ∂ x 2 {displaystyle {frac {partial u}{partial t}}=alpha {frac {partial ^{2}u}{partial x^{2}}}}

где u(t,x) — температура, и α — положительная константа, описывающая скорость распространения тепла. Задача Коши ставится следующим образом:

U (0 , x) = f (x) {displaystyle u(0,x),=f(x)},

где f(x) — произвольная функция.

Уравнение колебания струны

Уравнение относится к гиперболическому типу. Здесь u(t,x) — смещение струны из положения равновесия, или избыточное давление воздуха в трубе, или магнитуда электромагнитного поля в трубе, а c — скорость распространения волны. Для того, чтобы сформулировать задачу Коши в начальный момент времени, следует задать смещение и скорость струны в начальный момент времени:

u (0 , x) = f (x) , {displaystyle u(0,x)=f(x),} ∂ u ∂ t (0 , x) = g (x) , {displaystyle {dfrac {partial u}{partial t}}(0,x)=g(x),}

Двумерное уравнение Лапласа

Связь с аналитическими функциями

Вещественная и мнимая части любой голоморфной функции f {displaystyle f} комплексной переменной z = x + i y {displaystyle z=x+iy} являются сопряжённо гармоническими функциями: они обе удовлетворяют уравнению Лапласа и их градиенты ортогональны. Если f=u+iv, то условия Коши-Римана утверждают следующее:

∂ u ∂ x = ∂ v ∂ y , ∂ v ∂ x = − ∂ u ∂ y , {displaystyle {frac {partial u}{partial x}}={frac {partial v}{partial y}},quad {frac {partial v}{partial x}}=-{frac {partial u}{partial y}},}

Складывая и вычитая уравнения друг из друга, получаем:

∂ 2 u ∂ x 2 + ∂ 2 u ∂ y 2 = 0 , ∂ 2 v ∂ x 2 + ∂ 2 v ∂ y 2 = 0. {displaystyle {frac {partial ^{2}u}{partial x^{2}}}+{frac {partial ^{2}u}{partial y^{2}}}=0,quad {frac {partial ^{2}v}{partial x^{2}}}+{frac {partial ^{2}v}{partial y^{2}}}=0.}

Также можно показать, что любая гармоническая функция является вещественной частью некоторой аналитической функции.

Граничные задачи

Граничные задачи ставятся следующим образом: найти функцию u, которая удовлетворяет уравнению Лапласа во всех внутренних точках области S, а на границе области ∂ S {displaystyle partial S} — некоторому условию. В зависимости от вида условия различают следующие краевые задачи:

Решение уравнений математической физики

Существует два вида методов решения данного типа уравнений:

• аналитический, при котором результат выводится различными математическими преобразованиями;
• численный, при котором полученный результат соответствует действительному с заданной точностью, но который требует много рутинных вычислений и поэтому выполним только при помощи вычислительной техники (ЭВМ).

Аналитическое решение

Аналитические решения уравнений математической физики можно получить различными способами. Например:

• Используя функцию Грина ;
• Используя метод разделения переменных Фурье;
• С помощью теории потенциала ;
• Используя формулу Кирхгофа .

Эти методы разработаны для различных типов уравнений и в некоторых простых случаях позволяют получить решение в виде некоторой формулы или сходящегося ряда, например для

Теоретический минимум

В математической физике при рассмотрении задач, связанных с решением уравнений в частных производных второго порядка, всегда концентрируются на анализе некоторых основных уравнений: Пуассона, теплопроводности, волнового уравнения. Связано это с возможностью приведения уравнений второго порядка к т.н. каноническому виду, а именно к тем самым перечисленным только что уравнениям.

Рассмотрим уравнение второго порядка общего вида:,где . При этом будем считать без ограничения общности, что матрица коэффициентов симметрическая, т.е. (это фактически требование независимости смешанных производных от порядка дифференцирования). Далее будем называть эту матрицу матрицей старших коэффициентов. Строго говоря, одно и то же уравнение в различных точках может относиться к разным типам классификации. Пример будет приведён позже. В связи с этим замечанием будем говорить о матрице старших коэффициентов в определённой точке. Считаем, что матрица старших коэффициентов представляет собой матрицу некоторой квадратичной формы. Эту форму можно привести к нормальному виду, т.е. диагональному виду с коэффициентами, равными по модулю нулю или единице. Напомним, что число положительных коэффициентов называется положительным индексом инерции квадратичной формы, число отрицательных коэффициентов – отрицательным индексом формы, а число нулевых коэффициентов – дефектом формы. Уравнения можно классифицировать при помощи этих трёх чисел, которые и будем указывать в порядке их перечисления: . Сумма этих трёх чисел равна количеству независимых переменных. При этом ясно, что умножение всего уравнения на минус единицу приведёт к тому, что все элементы матрицы старших коэффициентов поменяют знак. Следовательно, положительный и отрицательный индексы соответствующей формы поменяются ролями. Таким образом, уравнения и принадлежат к одному типу классификации.Перечислим основные классы уравнений: — гиперболическое — параболическое — эллиптическое — ультрагиперболическое — эллиптико-параболическоеПоследние два типа уравнений в стандартных курсах не обсуждаются.

Словесно эту классификацию можно сформулировать следующим образом. Уравнение гиперболическое, если дефект соответствующей квадратичной формы равен нулю, а один из индексов равен единице. Уравнение параболическое, если его форма имеет равный единице дефект и все коэффициенты одного знака. Уравнение эллиптическое, если дефект его формы равен нулю и все коэффициенты имеют одинаковый знак.

Примеры уравнений различных типов

Пример 1. Уравнение теплопроводности.Уравнение параболического типа.

Пример 2. Волновое уравнение.Уравнение гиперболического типа.

Пример 3. Уравнение Пуассона.В частности, если справа стоит нуль, то получается уравнение Лапласа.

Пример 4. Уравнение Гельмгольца.Уравнение эллиптического типа.

Пример 5. Уравнение Трикоми.Если , то уравнение эллиптическое; если , то уравнение параболическое; если , то уравнение гиперболическое.

Подробнее рассмотрим случай, когда неизвестная функция имеет всего два аргумента:.Коэффициенты являются функциями переменных и (в принципе, возможна зависимость и от неизвестной функции (в этом случае уравнение будет квазилинейным; мы ограничиваемся линейными уравнениями). Уравнение общего вида может быть упрощено путём замены независимых переменных — приведено к каноническому виду. Этот канонический вид, как и вид замены определяется характеристическим уравнением.Характеристическое уравнение, будучи квадратным уравнением относительно производной сразу распадается на два.Знак подкоренного выражения и определяет тип уравнения.

Гиперболические уравненияЭто случай, когда . Общие интегралы характеристического уравнения .Выполняется замена .

Параболические уравнения.Выполняется замена , где — произвольная дважды дифференцируемая функция, для которой выполняется условие .

Эллиптические уравненияЭто случай, когда . Общий интеграл характеристического уравнения . Выполняется замена.

Рассмотрим несколько примеров, в каждом из которых требуется привести уравнение к каноническому виду. Центральную роль в этих примерах играет техниказамены переменных, потому что саму замену указать обычно довольно просто. Совсем просто выполняется линейная замена переменных (случай уравнения спостоянными коэффициентами).Замечание. Разумеется при замене переменных есть некоторая свобода. Например, в любом случае замена определяется с точностью до знака, не играющего существенной роли в преобразовании производных. Также неоднозначность вносит в случае параболического уравнения свобода выбора второй функции для замены переменных, ограниченная весьма слабыми условиями.

Примеры приведения уравнений второго порядка к каноническому виду

Пример 1. Случай линейной замены переменных в уравнении гиперболического типа.

.Исходное уравнение, таким образом, относится к гиперболическому типу. Находим общие интегралы найденных уравнений:.Вводим замену . Преобразуем производные. В данном случае можно считать, что функция зависит от переменных , которые в свою очередь зависят от старых переменных :..

Пример 2. Случай линейной замены переменных в уравнении эллиптического типа.

Составляем характеристическое уравнение:.Исходное уравнение, таким образом, относится к эллиптическому типу. Находим общий интеграл любого из найденных уравнений:.Вводим замену . Преобразуем производные совершенно аналогично тому, как это делалось в примере 1.После подстановки этих производных в исходное уравнение получим.

Пример 3. Случай линейной замены переменных в уравнении параболического типа.

Составляем характеристическое уравнение:.Исходное уравнение, таким образом, относится к параболическому типу. Находим общий интеграл найденного уравнения:.Отсюда понятно, какой может быть выбрана одна переменная: . Вторую переменную следует выбрать самостоятельно.Обычно её выбирают наиболее простой, чтобы не усложнять вычисления. Рассмотрим два варианта, чтобы посмотреть, как влияет выбор второйпеременной на окончательный вид уравнения. Сначала положим . Снова преобразуем производные аналогично примеру 1.После подстановки этих производных в исходное уравнение получим

Ранее рассматривались обыкновенныедифференциальные уравнения. Их решениязависят лишь от одной переменной:,и т. д. Во многих практических задачахискомые функции зависят от несколькихпеременных, и описывающие такие задачиуравнения могут содержать частныепроизводные искомых функций. Ониназываютсяуравнениями с частнымипроизводными.

К решению дифференциальных уравненийс частными производными приводят,например, многие задачи механики сплошныхсред. Здесь в качестве искомых функцийобычно служат плотность, температура,напряжение и др., аргументами которыхявляются координаты рассматриваемойточки пространства, а также время.

Полная математическая постановка задачинаряду с дифференциальными уравнениямисодержит также некоторые дополнительныеусловия. Если решение ищется в ограниченнойобласти, то задаются условия на еегранице, называемые граничными (краевыми)условиями. Такие задачи называютсякраевыми задачами для уравнений счастными производными.

Если одной из независимых переменныхв рассматриваемой задаче является времяt, то задаются некоторые условия(например, значения искомых параметров)в начальный момент,называемые начальными условиями. Задача,которая состоит в решении уравненияпри заданных начальных условиях,называется задачей Коши для уравненияс частными производными. При этом задачарешается в неограниченном пространствеи граничные условия не задаются.

Задачи, при формулировке которых ставятсяграничные и начальные условия, называютсянестационарными (или смешанными) краевымизадачами. Получающиеся при этом решенияменяются с течением времени.

Таким образом, математические моделифизических и иных процессов описываютсяс помощью дифференциальных уравненийв частных производных. Аргументамифункций этих уравнений являютсяпространственные координатыи время.

Уравнения первого порядка.Уравненияпервого порядка называются такжеуравнениями переноса. Это объясняетсятем, что такие уравнения описываютпроцессы переноса частиц в средах,распространения возмущений и т. п.

Его решение представляет интерес нетолько с практической точки зрения; веще большей степени это уравнениеполезно при разработке и исследованииразностных схем.

Будем считать, что искомая функциязависит от времении одной пространственной переменнойх. Тогда линейное уравнение переносаможет быть записано в виде

.

Здесь‑ скорость переноса.

Уравнения второго порядка.Линейнымуравнением в частных производных второгопорядка называется соотношение междуфункциейилии ее частными производными вида.

(1)

Если переменная функциязависит оти,то уравнение может быть записаноследующим образом:

(2)

В случае если,то уравнения 1-2 называются однородными,иначе ‑ неоднородными.

Если,то уравнение (2) относится к классуэллиптических уравнений;

если,то ‑ это гиперболическое уравнение;

если‑ параболическое уравнение.

Когдане имеет постоянного знака, получаетсяуравнение смешанного типа.

К классическим эллиптическим уравнениямотносятся:

Уравнение Лапласа,которое используется для описаниямагнитных и стационарных тепловыхполей;

Уравнение Пуассона,которое применяется в электростатике,теории упругости и других науках;

Уравнение Гельмголъца,описывающее установившиеся колебательныепроцессы.

Оператор Лапласа:

в одномерном случае;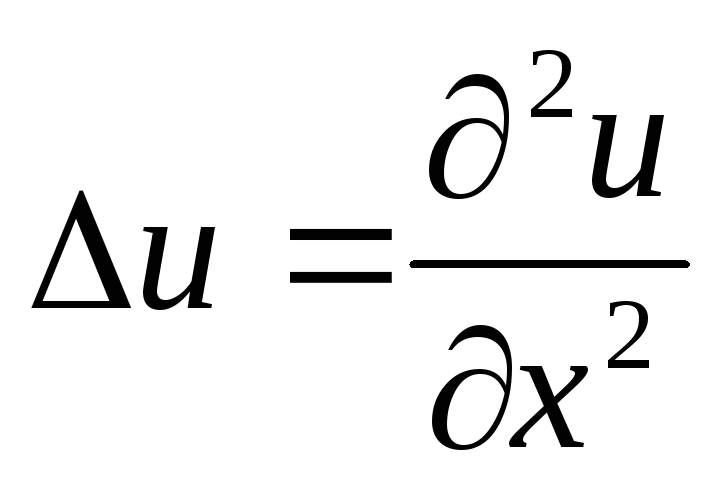

в двумерном случае;

в трехмерном случае.

Среди гиперболических уравнений можновыделить:

Волновые уравнения:

одномерное,которое описывает вынужденные колебанияструны;

двумерное,которое описывает колебания мембраны.

Телеграфное уравнение,которое описывает изменение потенциалав линиях электропередачи. Здесь— коэффициент самоиндукции, емкость,сопротивление, характеристика потерьна единицу длины линии.

К классическим параболическим уравнениямотносится уравнение теплопроводности.

Для нахождения единственного решениядифференциального уравнения в частныхпроизводных необходимо задать начальныеи граничные условия. Начальными условиямипринято называть условия, заданные вначальный момент времени.Граничные условия задаются при различныхзначениях пространственных переменных.Для эллиптических уравнений задаютсятолько граничные условия, которые можноразделить на три класса:

Условие Дирихле— в этом случае на границе области Г, вкоторой ищется решение, задана некаянепрерывная функция.В одномерном случае это условие принимаетвид:игде— интервал, на котором ищется решениеодномерной задачи;

Условие Неймана— в этом случае на границе области Гзадана производная по направлениювнешней нормали;

Смешанное условие.

Для параболических уравнений, кромеграничных условий, необходимо определитьодно начальное, которое может бытьтаким:.

В случае гиперболических уравненийначальные условия могут быть следующимии.

Решение ряда дифференциальных уравненийв частных производных может быть полученоаналитически. Одним из наиболее частоиспользуемых методов является методразделения переменных (метод Фурье).Рассмотрим этот метод подробнее.

О методах решения дифференциальныхуравнений в частных производных.

Решение простейших задач для уравненийс частными производными в ряде случаевможет быть проведено аналитическимиметодами, рассматриваемыми всоответствующих разделах математики.Это относится в основном к некоторымуравнениям первого порядка, а также куравнениям второго порядка с постояннымикоэффициентами. Аналитические методыполезны не только тем, что дают возможностьполучать общие решения, которые могутбыть использованы многократно. Ониимеют также огромное значение дляпостроения численных методов. Проверкаразностных схем на известных решенияхпростейших уравнений позволяет оценитьэти схемы, выяснить их сильные и слабыестороны.

Среди численных методовширокораспространенными являются разностныеметоды. Они основаны на введении некоторойразностной сетки в рассматриваемойобласти. Значения производных, начальныеи граничные условия выражаются череззначения функций в узлах сетки, врезультате чего получается системаалгебраических уравнений, называемаяразностной схемой. Решая эту системууравнений, можно найти в узлах сеткизначения сеточных функций, которыеприближенно считаются равными значениямискомых функций.

Приведенные уравнения называютсяуравнениями математической физики.К их решению сводятся многие прикладныезадачи. Прежде чем переходить к обсуждениючисленных методов решения указанныхуравнений, рассмотрим основные вопросыпостроения разностных схем.

2. Введение в сеточные методы, понятиясетка, шаблон, слой.

О построении разностных схем. Как ужеотмечалось, построение разностных схемрешения уравнений с частными производнымиосновано на введении сетки в рассматриваемомпространстве. Узлы сетки являютсярасчетными точками.

Пример простейшей прямоугольной областиG(x, у)с границей Г в двумерном случаепоказан на рис 1,а. Стороны прямоугольника,делятся на элементарные отрезки точками,и,.Через эти точки проводятся два семействакоординатных прямых,образующих сетку с прямоугольнойячейкой. Любой узел этой сетки, номеркоторого (),определяется координатами ().

аб

Рис. 1. Прямоугольнаясетка (а),элемент трехмерной сетки (б)

Узлы сетки, лежащие на границе Г областиG, называются граничными узлами. Всеостальные узлы ‑ внутренними.

Аналогично вводятся сетки для многомерныхобластей. На рис. 1,бпоказан элементсетки в виде прямоугольного параллелепипедадля трехмерной области.

Шаблон– комбинация используемыхузлов

Поскольку начальные и граничные условияпри постановке задач формулируются награнице расчетной области, то их можносчитать заданными в граничных узлахсетки. Иногда граничные точки областине являются узлами сетки, что имеетместо для областей сложной формы. Тогдалибо вводят дополнительные узлы напересечении координатных линий сграницей, либо границу приближеннозаменяют ломаной, проходящей черезблизкие к границе узлы. На эту ломануюпереносятся граничные условия.

В ряде случаев сложные криволинейныеобласти с помощью перехода к новымнезависимым переменным удается свестик простейшему виду. Например, четырехугольнуюобласть G, изображенную на рис. 2,можно привести к единичному квадратуG»путем введения новых переменных£, ц вместо #, у с помощью соотношений

К новым переменным нужно преобразоватьуравнения, а также начальные и граничныеусловия. В области G»можно ввестипрямоугольную сетку, при этом в областиGей будет соответствовать сетка снеравномерно расположенными узлами икриволинейными ячейками,

В дальнейшем при построении разностных схем мы для простоты будем использоватьпрямоугольные сетки (или с ячейками ввиде прямоугольных параллелепипедовв трехмерном случае), а уравнения будемзаписывать в декартовых координатах().На практике приходится решать задачив различных криволинейных системахкоординат: полярной, цилиндрической,сферической н др. Например, если расчетнуюобласть удобно задать в полярныхкоординатах (),то в ней сетка вводится с шагамиисоответственно по радиус-вектору иполярному углу.

Иногда и в простой расчетной областивводят неравномерную сетку. В частности,в ряде случаев необходимо проводитьсгущение узлов для более точного расчетав некоторых частях рассматриваемойобласти. При этом области сгущения узловлибо известны заранее, либо определяютсяв процессе решения задачи (например, взависимости от градиентов искомыхфункций).

Для построения разностной схемы, как ив случае обыкновенных дифференциальныхуравнений, частные производные вуравнении заменяются конечно-разностнымисоотношениями по некоторому шаблону(см. гл. 3, § 1). При этом точные значенияискомой функции Uзаменяютсязначениями сеточной функции и в узлахразностной сетки.

В качестве примера построим некоторыеразностные схемы для решения уравнениятеплопроводности при заданных начальныхи граничных условиях. Запишем смешаннуюкраевую задачу в виде

,(6)

где‑ начальное распределение температурыU(приt= 0);‑ распределение температуры на концахрассматриваемого отрезка (х= 0, 1) влюбой момент времениt. Заметим, чтоначальные и граничные условия должныбыть согласованы, т. е.,.

Введем равномерную прямоугольную сеткус помощью координатных линий,и,,и‑ соответственно шаги сетки понаправлениямхиt. Значенияфункции в узлах сетки обозначим.Эти значения заменим соответствующимизначениями сеточной функциикоторые удовлетворяют разностной схеме.

Заменяя в исходном уравнении (6) частныепроизводные искомой функции с помощьюотношений конечных разностей, получаемразностную схему

(7)

В записи этой схемы для каждого узлаиспользован шаблон, изображенный нарис. 2, а.

Для одного и того же уравнения можнопостроить различные разностные схемы.В частности, если воспользоватьсяшаблоном, изображенным на рис. 2, б,то вместо (7) получим разностную схему

(8)

И в том и другом случае получаетсясистема алгебраических уравнений дляопределения значений сеточной функцииво внутренних узлах. Значения в граничныхузлах находятся из граничных условий

Совокупность узлов при t= const, т. е.при фиксированном значении,называетсяслоем. Схема (7) позволяетпоследовательно находить значения,на-мслое через соответствующие значенияна-мслое. Такие схемы называютсяявными.

Для начала счета при j= 1 необходимо решение на начальном слое.Оно определяется начальным условием

В отличие от явной схемы каждое разностноеуравнение (8) содержит на каждом новомслое значения неизвестных в трех точках,поэтому нельзя сразу определить этизначения через известное решение напредыдущем слое. Такие схемы называютсянеявными. При этом разностная схема(8) состоит из линейных трехточечныхуравнений, т. е. каждое уравнение содержитнеизвестную функцию в трех точкахданного слоя. Такие системы линейныхуравнений с трехдиагональной матрицеймогут быть решены методом прогонкb,в результате чего будут найдены значениясеточной функции в узлах.

Заметим, что в рассмотренном примеремы получаем двухслойные схемы, когдав каждое разностное уравнение входятзначения функции из двух слоев ‑нижнего, на котором решение уже найдено,и верхнего, в узлах которого решениеищется.

С помощью рассматриваемого способапостроения разностных схем, когдавходящие в уравнение отдельные частныепроизводные заменяются конечно-разностнымисоотношениями для сеточной функции(или сеточными выражениями), могут бытьсозданы многослойные схемы, а такжесхемы высоких порядков точности.

Уравнение Лапласа.Многие стационарныефизические задачи (исследованияпотенциальных течений жидкости,определение формы нагруженной мембраны,задачи теплопроводности и диффузии встационарных случаях и др.) сводятся крешению уравненияПуассонавида

1

Если,то это уравнение называется уравнениемЛапласа. Для простоты будемрассматривать двумерное уравнениеЛапласа

2

Решение этого уравнения будем искатьдля некоторой ограниченной области Gизменения независимых переменныхх,у. Границей областиGявляетсязамкнутая линияL. Для полнойформулировки краевой задачи кромеуравнения Лапласа нужно задать граничноеусловие на границеL. Примем его ввиде

3

Задача, состоящая в решении уравненияЛапласа (или Пуассона) при заданныхзначениях искомой функции на границерасчетной области, называется задачейДирихле.

Одним из способов решения стационарныхэллиптических задач, в том числе икраевой задачи, является их сведение крешению некоторой фиктивной нестационарнойзадачи (гиперболической или параболической),найденное решение которой при достаточнобольших значениях tблизко к решениюисходной задачи. Такой способ решенияназываетсяметодом установления.

Поскольку решение U (х, у)нашегоуравнения (2) не зависит от времени, томожно в это уравнение добавить равныйнулю (при точном решении) член.Тогда уравнение (2) примет вид

4

Это ‑ известное нам уравнениетеплопроводности, для которого ужестроились разностные схемы. Остаетсятолько задать начальное условие. Егоможно принять практически в произвольномвиде, согласованном с граничнымиусловиями. Положим

5

Граничное условие (3) при этом остаетсястационарным, т. е. не зависящим отвремени.

Процесс численного решения уравнения(4) с условиями (3), (5) состоит в переходеприот произвольного значения (5) к искомомустационарному решению. Счет ведется довыхода решения на стационарный режим.Естественно, ограничиваются решениемпри некотором достаточно большом,если искомые значения на двухпоследовательных слоях совпадают сзаданной степенью точности.

Метод установления фактически представляетитерационный процесс решения задачи,причем на каждой итерации значенияискомой функции получаются путемчисленного решения некоторойвспомогательной задачи.

Для решения задачи Дирихле можно такжепостроить разностную схему путемаппроксимации уравнения (2). Введем впрямоугольной области G сетку с помощьюкоординатных прямых х= const и у =const. Примем для простоты значения шаговпо переменнымхиуравнымиh(предполагается, что стороны области Gсоизмеримы). Значения функцииUвузлахзаменим значениями сеточной функции.Тогда, аппроксимируя в уравнении (2)вторые производные с помощью отношенийконечных разностей, получим разностноеуравнение (шаблон изображен на рис.):

(6)

Данное уравнение можно представить ввиде системы линейных алгебраическихуравнений относительно значений сеточнойфункции в узлах. Эту систему можнозаписать в виде

Значения сеточной функции в узлах,расположенных на границе расчетнойобласти, могут быть найдены из граничногоусловия (3):

В теории разностных схем доказывается,что решение построенной разностнойзадачи существует, а сама схема устойчива.

Каждое уравнение системы (7) (за исключениемтех, которые соответствуют узлам,расположенным вблизи границ) содержитпять неизвестных. Одним из наиболеераспространенных методов решения этойсистемы линейных уравнений являетсяитерационный метод. Каждое из уравненийзаписываем в виде, разрешенном относительнозначенияв центральном узле (см. рис.):

Итерационный процесс контролируетсямаксимальным отклонением М значенийсеточной функции в узлах для двухпоследовательных итераций. Если еговеличина достигнет некоторого заданногомалого числа,итерации прекращаются.

Решение уравнения Лапласа в Mathcad.Для решения уравнений Лапласа и ПуассонавMathcadпредусмотренывстроенные функцииrelaxиmultigrid.

3. Решение дифференциальных уравненийс частными производными методом конечныхразностей.

4. Решение эллиптических, параболическихи гиперболических уравнений.

5. Нестационарные задачи.

6. Построение явной и неявной разностныхсхем для одномерного уравнениятеплопроводности.

7. Вопросы аппроксимации, устойчивостии сходимости.

8. Метод прогонки.

9. Аппроксимация дифференциальныхуравнений в частных производных системойобыкновенных дифференциальных уравнений(метод прямых).

10. Стационарные задачи, разностныесхемы, счет на установление.

11. Вариационно-разностные методы.

12. Метод конечных элементов.