У треугольника какие стороны. Что такое остроугольный треугольник

Еще дети дошкольного возраста знают, как выглядит треугольник. А вот с тем, какие они бывают, ребята уже начинают разбираться в школе. Одним из видов является тупоугольный треугольник. Понять, что это такое, проще всего, если увидеть картинку с его изображением. А в теории это так называют "простейший многоугольник" с тремя сторонами и вершинами, одна из которых является

Разбираемся с понятиями

В геометрии различают такие виды фигур с тремя сторонами: остроугольный, прямоугольный и тупоугольный треугольники. При этом свойства этих простейших многоугольников одинаковы для всех. Так, для всех перечисленных видов будет соблюдаться такое неравенство. Сумма длин любых двух сторон обязательно будет больше протяженности третьей стороны.

Но для того чтобы быть уверенным, что речь идет именно о законченной фигуре, а не о наборе отдельных вершин, необходимо проверить, чтобы соблюдалось основное условие: сумма углов тупоугольного треугольника равняется 180 о. Это же верно и для других видов фигур с тремя сторонами. Правда, в тупоугольном треугольнике один из углов будет еще больше 90 о, а два оставшихся обязательно будут острыми. При этом именно наибольший угол будет находиться напротив самой длинной стороны. Правда, это далеко не все свойства тупоугольного треугольника. Но и зная лишь эти особенности, школьники могут решать многие задачи по геометрии.

Для каждого многоугольника с тремя вершинами верно и то, что, продолжая любую из сторон, мы получим угол, размер которого будет равен сумме двух несмежных с ним внутренних вершин. Периметр тупоугольного треугольника рассчитывается так же, как и для других фигур. Он равняется сумме длин всех его сторон. Для определения математиками были выведены различные формулы, в зависимости от того, какие изначально присутствуют данные.

Правильное начертание

Одним из важнейших условий решения задач по геометрии является верный рисунок. Часто учителя математики говорят о том, что он поможет не только наглядно представить, что дано и что от вас требуется, но на 80% приблизиться к правильному ответу. Именно поэтому важно знать, как построить тупоугольный треугольник. Если вам нужна просто гипотетическая фигура, то вы можете нарисовать любой многоугольник с тремя сторонами так, чтобы один из углов был больше 90 о.

Если даны определенные значения длин сторон или градусы углов, то чертить тупоугольный треугольник необходимо в соответствии с ними. При этом необходимо стараться максимально точно изобразить углы, высчитывая их при помощи транспортира, и пропорционально данным в задании условиям отобразить стороны.

Основные линии

Зачастую школьникам мало знать только то, как должны выглядеть те или иные фигуры. Они не могут ограничиться лишь информацией о том, какой треугольник тупоугольный, а какой прямоугольный. Курсом математики предусмотрено, что их знания об основных особенностях фигур должны быть более полными.

Так, каждому школьнику должно быть понятно определение биссектрисы, медианы, серединного перпендикуляра и высоты. Кроме того, он должен знать и их основные свойства.

Так, биссектрисы делят угол пополам, а противоположную сторону - на отрезки, которые пропорциональны прилегающим сторонам.

Медиана делит любой треугольник на два равных по площади. В точке, в которой они пересекаются, каждая из них разбивается на 2 отрезка в пропорции 2: 1, если смотреть от вершины, из которой она вышла. При этом большая медиана всегда проведена к его наименьшей стороне.

Не меньше внимания уделяется и высоте. Это перпендикуляр к противоположной от угла стороне. Высота тупоугольного треугольника имеет свои особенности. Если она проведена из острой вершины, то она попадает не на сторону этого простейшего многоугольника, а на ее продолжение.

Серединный перпендикуляр - это отрезок, который выходит из центра грани треугольника. При этом он расположен к ней под прямым углом.

Работа с окружностями

В начале изучения геометрии детям достаточно понять, как начертить тупоугольный треугольник, научиться отличать его от остальных видов и запомнить его основные свойства. А вот старшеклассникам этих знаний уже мало. Например, на ЕГЭ часто встречаются вопросы про описанные и вписанные окружности. Первая из них касается всех трех вершин треугольника, а вторая имеет по одной общей точке со всеми сторонами.

Построить вписанный или описанный тупоугольный треугольник уже намного сложнее, ведь для этого необходимо для начала выяснить, где должен находиться центр окружности и ее радиус. Кстати, необходимым инструментом станет в этом случае не только карандаш с линейкой, но и циркуль.

Те же сложности возникают при построении вписанных многоугольников с тремя сторонами. Математиками были выведены различные формулы, которые позволяют определить их месторасположение максимально точно.

Вписанные треугольники

Как уже было сказано ранее, если круг проходит через все три вершины, то это называется описанной окружностью. Главным ее свойством является то, что она единственная. Чтобы выяснить, как должна располагаться описанная окружность тупоугольного треугольника, необходимо помнить, что ее центр находится на пересечении трех серединных перпендикуляров, которые идут к сторонам фигуры. Если в остроугольном многоугольнике с тремя вершинами эта точка будет находиться внутри него, то в тупоугольном - за его пределами.

Зная, например, что одна из сторон тупоугольного треугольника равна его радиусу, можно найти угол, который лежит напротив известной грани. Его синус будет равен результату от деления длины известной стороны на 2R (где R - это радиус окружности). То есть sin угла будет равен ½. Значит, угол будет равен 150 о.

Если вам необходимо найти радиус описанной окружности тупоугольного треугольника, то вам пригодятся сведения о длине его сторон (c, v, b) и его площади S. Ведь радиус высчитывается так: (c х v х b) : 4 х S. Кстати, неважно, какого именно у вас вида фигура: разносторонний тупоугольный треугольник, равнобедренный, прямо- или остроугольный. В любой ситуации, благодаря приведенной формуле, вы можете узнать площадь заданного многоугольника с тремя сторонами.

Описанные треугольники

Также довольно часто приходится работать со вписанными окружностями. По одной из формул, радиус такой фигуры, умноженный на ½ периметра, будет равняться площади треугольника. Правда, для ее выяснения вам необходимо знать стороны тупоугольного треугольника. Ведь для того чтобы определить ½ периметра, необходимо сложить их длины и разделить на 2.

Чтобы понять, где должен находиться центр круга, вписанного в тупоугольный треугольник, необходимо провести три биссектрисы. Это линии, которые делят углы пополам. Именно на их пересечении и будет находиться центр окружности. При этом он будет равноудален от каждой из сторон.

Радиус такой окружности, вписанной в тупоугольный треугольник, равняется из частного (p-c) х (p-v) х (p-b) : p. При этом p - это полупериметр треугольника, c, v, b - его стороны.

Стандартные обозначения

Треугольник с вершинами A , B и C обозначается как (см. рис.). Треугольник имеет три стороны:

Длины сторон треугольника обозначаются строчными латинскими буквами (a, b, c):

Треугольник имеет следующие углы:

Величины углов при соответствующих вершинах традиционно обозначаются греческими буквами (α, β, γ).

Признаки равенства треугольников

Треугольник на евклидовой плоскости однозначно (с точностью до конгруэнтности) можно определить по следующим тройкам основных элементов:

1. a, b, γ (равенство по двум сторонам и углу лежащему между ними);
2. a, β, γ (равенство по стороне и двум прилежащим углам);
3. a, b, c (равенство по трём сторонам).

Признаки равенства прямоугольных треугольников:

1. по катету и гипотенузе;
2. по двум катетам;
3. по катету и острому углу;
4. по гипотенузе и острому углу.

Некоторые точки в треугольнике - «парные». Например, существует две точки, из которых все стороны видны либо под углом в 60°, либо под углом в 120°. Они называются точками Торричелли . Также существует две точки, проекции которых на стороны лежат в вершинах правильного треугольника. Это - точки Аполлония . Точки и такие, что и называются точками Брокара .

Прямые

В любом треугольнике центр тяжести, ортоцентр и центр описанной окружности лежат на одной прямой, называемой прямой Эйлера .

Прямая, проходящая через центр описанной окружности и точку Лемуана, называется осью Брокара . На ней лежат точки Аполлония. Также на одной прямой лежат точки Торричелли и точка Лемуана. Основания внешних биссектрис углов треугольника лежат на одной прямой, называемой осью внешних биссектрис . На одной прямой лежат также точки пересечения прямых, содержащих стороны ортотреугольника, с прямыми, содержащими стороны треугольника. Эта прямая называется ортоцентрической осью , она перпендикулярна прямой Эйлера.

Если на описанной окружности треугольника взять точку, то её проекции на стороны треугольника будут лежать на одной прямой, называемой прямой Симсона данной точки. Прямые Симсона диаметрально противоположных точек перпендикулярны.

Треугольники

• Треугольник с вершинами в основаниях чевиан, проведённых через данную точку, называется чевианным треугольником этой точки.
• Треугольник с вершинами в проекциях данной точки на стороны называется подерным или педальным треугольником этой точки.
• Треугольник в вершинами во вторых точках пересечения прямых, проведённых через вершины и данную точку, с описанной окружностью, называют окружностно-чевианным треугольником . Окружностно-чевианный треугольник подобен подерному.

Окружности

• Вписанная окружность - окружность , касающаяся всех трёх сторон треугольника. Она единственна. Центр вписанной окружности называется инцентром .
• Описанная окружность - окружность, проходящая через все три вершины треугольника. Описанная окружность также единственна.
• Вневписанная окружность - окружность, касающаяся одной стороны треугольника и продолжения двух других сторон. Таких окружностей в треугольнике три. Их радикальный центр - центр вписанной окружности срединного треугольника, называемый точкой Шпикера .

Середины трёх сторон треугольника, основания трёх его высот и середины трёх отрезков, соединяющих его вершины с ортоцентром, лежат на одной окружности, называемой окружностью девяти точек или окружностью Эйлера . Центр окружности девяти точек лежит на прямой Эйлера. Окружность девяти точек касается вписанной окружности и трёх вневписанных. Точка касания вписанной окружности и окружности девяти точек называется точкой Фейербаха . Если от каждой вершины отложить наружу треугольника на прямых, содержащих стороны, ортезки, равные по длине противоположным сторонам, то получившиеся шесть точек лежат на одной окружности - окружности Конвея . В любой треугольник можно вписать три окружности таким образом, что каждая из них касается двух сторон треугольника и двух других окружностей. Такие окружности называются окружностями Мальфатти . Центры описанных окружностей шести треугольников, на которые треугольник разбивается медианами, лежат на одной окружности, которая называется окружностью Ламуна .

В треугольнике есть три окружности, которые касаются двух сторон треугольника и описанной окружности. Такие окружности называют полувписанными или окружностями Веррьера . Отрезки, соединяющие точки касания окружностей Веррьера с описанной окружностью, пересекаются в одной точке, называемой точкой Веррьера . Она служит центром гомотетии , которая переводит описанную окружность во вписанную. Точки касания окружностей Веррьера со сторонами лежат на прямой, которая проходит через центр вписанной окружности.

Отрезки, соединяющие точки касания вписанной окружности с вершинами, пересекаются в одной точке, называемой точкой Жергонна , а отрезки, соединяющие вершины с точками касания вневписанных окружностей - в точке Нагеля .

Эллипсы, параболы и гиперболы

Вписанная коника (эллипс) и её перспектор

В треугольник можно вписать бесконечно много коник (эллипсов , парабол или гипербол). Если в треугольник вписать произвольную конику и соединить точки касания с противоположными вершинами, то получившиеся прямые пересекутся в одной точке, называемой перспектором коники. Для любой точки плоскости, не лежащей на стороне или на её продолжении существует вписанная коника с перспектором в этой точке.

Описанный эллипс Штейнера и чевианы, проходящие через его фокусы

В треугольник можно вписать эллипс, который касается сторон в серединах. Такой эллипс называется вписанным эллипсом Штейнера (его перспектором будет центроид треугольника). Описанный эллипс, который касается прямых, проходящих через вершины параллельно сторонам, называется описанным эллипсом Штейнера . Если аффинным преобразованием («перекосом») перевести треугольник в правильный, то его вписанный и описанный эллипс Штейнера перейдут во вписанную и описанную окружности. Чевианы, проведённые через фокусы описанного эллипса Штейнера (точки Скутина), равны (теорема Скутина). Изо всех описанных эллипсов описанный эллипс Штейнера имеет наименьшую площадь, а изо всех вписанных наибольшую площадь имеет вписанный эллипс Штейнера.

Эллипс Брокара и его перспектор - точка Лемуана

Эллипс с фокусами в точках Брокара называется эллипсом Брокара . Его перспектором служит точка Лемуана.

Свойства вписанной параболы

Парабола Киперта

Перспекторы вписанных парабол лежат на описанном эллипсе Штейнера. Фокус вписанной параболы лежит на описанной окружности, а директриса проходит через ортоцентр. Парабола, вписанная в треугольник, имеющая директрисой прямую Эйлера, называется параболой Киперта . Её перспектор - четвёртая точка пересечения описанной окружности и описанного эллипса Штейнера, называемая точкой Штейнера .

Гипербола Киперта

Если описанная гипербола проходит через точку пересечения высот, то она равносторонняя (то есть её асимптоты перпендикулярны). Точка пересечения асимптот равносторонней гиперболы лежит на окружности девяти точек.

Преобразования

Если прямые, проходящие через вершины и некоторую точку, не лежащую на сторонах и их продолжениях, отразить относительно соответствующих биссектрис, то их образы также пересекутся в одной точке, которая называется изогонально сопряжённой исходной (если точка лежала на описанной окружности, то получившиеся прямые будут параллельны). Изогонально сопряжёнными являются многие пары замечательных точек : центр описанной окружности и ортоцентр, центроид и точка Лемуана, точки Брокара. Точки Аполлония изогонально сопряжены точкам Торричелли, а центр вписанной окружности изогонально сопряжён сам себе. Под действием изогонального сопряжения прямые переходят в описанные коники, а описанные коники - в прямые. Так, изогонально сопряжены гипербола Киперта и ось Брокара, гипербола Енжабека и прямая Эйлера, гипербола Фейербаха и линия центров вписанной о описанной окружностей. Описанные окружности подерных треугольников изогонально сопряжённых точек совпадают. Фокусы вписанных эллипсов изогонально сопряжены.

Если вместо симметричной чевианы брать чевиану, основание которой удалено от середины стороны так же, как и основание исходной, то такие чевианы также пересекутся в одной точке. Получившееся преобразование называется изотомическим сопряжением . Оно также переводит прямые в описанные коники. Изотомически сопряжены точки Жергонна и Нагеля. При аффинных преобразованиях изотомически сопряжённые точки переходят в изотомически сопряжённые. При изотомическом сопряжении в бесконечно удалённую прямую перейдёт описанный эллипс Штейнера.

Если в сегменты, отсекаемые сторонами треугольника от описанного круга, вписать окружности, касающиеся сторон в основаниях чевиан, проведённых через некоторую точку, а затем соединить точки касания этих окружностей с описанной окружностью с противоположными вершинами, то такие прямые пересекутся в одной точке. Преобразование плоскости, сопоставляющее исходной точке получившуюся, называется изоциркулярным преобразованием . Композиция изогонального и изотомического сопряжений является композицией изоциркулярного преобразования с самим собой. Эта композиция - проективное преобразование , которое стороны треугольника оставляет на месте, а ось внешних биссектрис переводит в бесконечно удалённую прямую.

Если продолжить стороны чевианного треугольника некоторой точки и взять их точки пересечения с соответствующими сторонами, то полученные точки пересечения будут лежать на одной прямой, называемой трилинейной полярой исходной точки. Ортоцентрическая ось - трилинейная поляра ортоцентра; трилинейной полярой центра вписанной окружности служит ось внешних биссектрис. Трилинейные поляры точек, лежищих на описанной конике, пересекаются в одной точке (для описанной окружности это точка Лемуана, для описанного эллипса Штейнера - центроид). Композиция изогонального (или изотомического) сопряжения и трилинейной поляры является преобразованием двойственности (если точка, изогонально (изотомически) сопряжённая точке , лежит на трилинейной поляре точки , то трилинейная поляра точки, изогонально (изотомически) сопряжённой точке лежит на трилинейной поляре точки ).

Кубики

Соотношения в треугольнике

Примечание: в данном разделе , , - это длины трёх сторон треугольника, и , , - это углы, лежащие соответственно напротив этих трёх сторон (противолежащие углы).

Неравенство треугольника

В невырожденном треугольнике сумма длин двух его сторон больше длины третьей стороны, в вырожденном - равна. Иначе говоря, длины сторон треугольника связаны следующими неравенствами:

Неравенство треугольника является одной из аксиом метрики .

Теорема о сумме углов треугольника

Теорема синусов

,

где R - радиус окружности, описанной вокруг треугольника. Из теоремы следует, что если a < b < c, то α < β < γ.

Теорема косинусов

Теорема тангенсов

Прочие соотношения

Метрические соотношения в треугольнике приведены для :

Решение треугольников

Вычисление неизвестных сторон и углов треугольника, исходя из известных, исторически получило название «решения треугольников» . При этом используются приведенные выше общие тригонометрические теоремы.

Площадь треугольника

Частные случаи Обозначения

Для площади справедливы неравенства:

Вычисление площади треугольника в пространстве с помощью векторов

Пусть вершины треугольника находятся в точках , , .

Введём вектор площади . Длина этого вектора равна площади треугольника, а направлен он по нормали к плоскости треугольника:

Положим , где , , - проекции треугольника на координатные плоскости. При этом

и аналогично

Площадь треугольника равна .

Альтернативой служит вычисление длин сторон (по теореме Пифагора) и далее по формуле Герона .

Теоремы о треугольниках

Теорема Дезарга : если два треугольника перспективны (прямые, проходящие через соответственные вершины треугольников, пересекаются в одной точке), то их соответственные стороны пересекаются на одной прямой.

Теорема Сонда́ : если два треугольника перспективны и ортологичны (перпендикуляры, опущенные из вершин одного треугольника на стороны, противоположные соответственным вершинам треугольника, и наоборот), то оба центра ортологии (точки пересечения этих перпендикуляров) и центр перспективы лежат на одной прямой, перпендикулярной оси перспективы (прямой из теоремы Дезарга).

Признаки равенства прямоугольных треугольников

Типы треугольников

Рассмотрим три точки, не лежащие на одной прямой, и три отрезка, соединяющие эти точки (рис. 1).

Треугольником называют часть плоскости, ограниченную этими отрезками, отрезки называют сторонами треугольника, а концы отрезков (три точки, не лежащие на одной прямой) – вершинами треугольника.

В таблице 1 перечислены все возможные типы треугольников в зависимости от величины их углов .

Таблица 1 – Типы треугольников в зависимости от величины углов

Рисунок	Тип треугольника	Определение
	Остроугольный треугольник	Треугольник, у которого все углы острые , называют остроугольным
	Прямоугольный треугольник	Треугольник, у которого один из углов прямой , называют прямоугольным
	Тупоугольный треугольник	Треугольник, у которого один из углов тупой , называют тупоугольным

Остроугольный треугольник

Определение: Треугольник, у которого все углы острые , называют остроугольным

Прямоугольный треугольник

Определение: Треугольник, у которого один из углов прямой , называют прямоугольным

Тупоугольный треугольник

Определение: Треугольник, у которого один из углов тупой , называют тупоугольным

В зависимости от длин сторон выделяют два важных типа треугольников.

Таблица 2 – Равнобедренный и равносторонний треугольники

Рисунок	Тип треугольника	Определение
	Равнобедренный треугольник	боковыми сторонами , а третью сторону называют основанием равнобедренного треугольника
	Равносторонний (правильный) треугольник	Треугольник, у которого все три стороны равны, называют равносторонним или правильным треугольником

Равнобедренный треугольник

Определение: Треугольник, у которого две стороны равны, называют равнобедренным треугольником. В этом случае две равные стороны называют боковыми сторонами , а третью сторону называют основанием равнобедренного треугольника

Равносторонний (правильный) треугольник

Определение: Треугольник, у которого все три стороны равны, называют равносторонним или правильным треугольником

Признаки равенства треугольников

Треугольники называют равными , если их можно совместить наложением .

В таблице 3 приведены признаки равенства треугольников .

Таблица 3 – Признаки равенства треугольников

Рисунок	Название признака	Формулировка признака
	по двум сторонам и углу между ними
	Признак равенства треугольников по стороне и двум прилежащим к ней углам
	Признак равенства треугольников по трём сторонам

Признак равенства треугольников по двум сторонам и углу между ними

Формулировка признака . Если две стороны одного треугольника и угол между ними соответственно равны двум сторонам другого треугольника и углу между ними, то такие треугольники равны

Признак равенства треугольников по стороне и двум прилежащим к ней углам

Формулировка признака . Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны

Признак равенства треугольников по трём сторонам

Формулировка признака . Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны

Признаки равенства прямоугольных треугольников

Для сторон прямоугольных треугольников принято использовать следующие названия.

Гипотенузой называют сторону прямоугольного треугольника, лежащую против прямого угла (рис. 2), две другие стороны называют катетами .

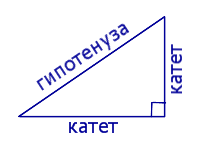
Таблица 4 – Признаки равенства прямоугольных треугольников

Рисунок	Название признака	Формулировка признака
	по двум катетам
	Признак равенства прямоугольных треугольников по катету и прилежащему острому углу
	Признак равенства прямоугольных треугольников по катету и противолежащему острому углу	Если катет и противолежащий острый угол одного прямоугольного треугольника соответственно равны катету и противолежащему острому углу другого прямоугольного треугольника, то такие прямоугольные треугольники равны
	Признак равенства прямоугольных треугольников по гипотенузе и острому углу	Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие прямоугольные треугольники равны
	Признак равенства прямоугольных треугольников по катету и гипотенузе	Если катет и гипотенуза одного прямоугольного треугольника соответственно равны катету и гипотенузе другого прямоугольного треугольника, то такие прямоугольные треугольники равны

Признак равенства прямоугольных треугольников по двум катетам

Формулировка признака . Если два катета одного прямоугольного треугольника соответственно равны двум катетам другого прямоугольного треугольника, то такие прямоугольные треугольники равны

Признак равенства прямоугольных треугольников по катету и прилежащему острому углу

Формулировка признака . Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого прямоугольного треугольника, то такие прямоугольные треугольники равны

Признак равенства прямоугольных треугольников по катету и противолежащему острому углу

Треугольник — это многоугольник с тремя сторонами (или тремя углами). Стороны треугольника обозначаются часто малыми буквами (а, b, c), которые соответствуют заглавным буквам, обозначающим противоположные вершины (A, B, C).

Если в треугольнике все три угла острые, то это остроугольный треугольник .

Если в треугольнике один из углов прямой, то это прямоугольный треугольник . Стороны, образующие прямой угол, называются катетами . Сторона, противоположная прямому углу, называется гипотенузой .

Если в треугольнике один из углов тупой, то это тупоугольный треугольник.

Треугольник равнобедренный , если две его стороны равны; эти равные стороны называются боковыми, а третья сторона называется основанием треугольника.

Треугольник равносторонний , если все его стороны равны.

Основные свойства треугольников

В любом треугольнике:

1. Против большей стороны лежит больший угол, и наоборот.

2. Против равных сторон лежат равные углы, и наоборот.
В частности, все углы в равностороннем треугольнике равны.

3. Сумма углов треугольника равна 180º .
Из двух последних свойств следует, что каждый угол в равностороннем
треугольнике равен 60º.

4. Продолжая одну из сторон треугольника, получаем внешний
угол. Внешний угол треугольника равен сумме внутренних углов,
не смежных с ним.

5. Любая сторона треугольника меньше суммы двух других сторон и больше
их разности.

Признаки равенства треугольников.

Треугольники равны, если у них соответственно равны:

A) две стороны и угол между ними;
b) два угла и прилегающая к ним сторона;
c) три стороны.

Признаки равенства прямоугольных треугольников.

Два прямоугольных треугольника равны, если выполняется одно из следующих условий:

1) равны их катеты;
2) катет и гипотенуза одного треугольника равны катету и гипотенузе другого;
3) гипотенуза и острый угол одного треугольника равны гипотенузе и острому углу другого;
4) катет и прилежащий острый угол одного треугольника равны катету и прилежащему острому углу другого;
5) катет и противолежащий острый угол одного треугольника равны катету и противолежащему острому углу другого.

Высота треугольника — это перпендикуляр, опущенный из любой вершины на противоположную сторону (или её продолжение). Эта сторона называется основанием треугольника. Три высоты треугольника всегда пересекаются в одной точке, называемой ортоцентром треугольника . Ортоцентр остроугольного треугольника расположен внутри треугольника, а ортоцентр тупоугольного треугольника — снаружи; ортоцентр прямоугольного треугольника совпадает с вершиной прямого угла.

Медиана — это отрезок, соединяющий любую вершину треугольника с серединой противоположной стороны. Три медианы треугольника пересекаются в одной точке, всегда лежащей внутри треугольника и являющейся его центром тяжести . Эта точка делит каждую медиану в отношении 2:1, считая от вершины.

Свойство медианы равнобедренного треугольника. В равнобедренном треугольнике медиана, проведённая к основанию, является биссектрисой и высотой.

Биссектриса — это отрезок биссектрисы угла от вершины до точки пересечения с противоположной стороной. Три биссектрисы треугольника пересекаются в одной точке, всегда лежащей внутри треугольника и являющейся центром вписанной окружности . Биссектриса делит противоположную сторону на части, пропорциональные прилегающим сторонам.

Срединный перпендикуляр — это перпендикуляр, проведенный из средней точки отрезка (стороны). Три срединных перпендикуляра треугольника пересекаются в одной точке, являющейся центром описанной окружности. В остроугольном треугольнике эта точка лежит внутри треугольника; в тупоугольном — снаружи; в прямоугольном — в середине гипотенузы. Ортоцентр, центр тяжести, центр описанной и центр вписанной окружности совпадают только в равностороннем треугольнике.

Средняя линия треугольника — это отрезок, соединяющий середины двух его сторон.

Свойство средней линии треугольника . Средняя линия треугольника, соединяющая середины двух данных сторон, параллельна третьей стороне и равна её половине.

Теорема Пифагора. В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов. c 2 = a 2 + b 2 .

Доказательства теоремы Пифагора можно посмотреть здесь.

Теорема синусов . Стороны треугольника пропорциональны синусам противолежащих углов.

Теорема косинусов. Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними.

Доказательства теоремы синусов и теоремы косинусов можно посмотреть здесь .

Теорема о сумме углов в треугольнике. Сумма внутренних углов треугольника равна 180°.

Теорема о внешнем угле треугольника . Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.

Сегодня мы отправляемся в страну Геометрия, где познакомимся с различными видами треугольников.

Рассмотрите геометрические фигуры и найдите среди них «лишнюю» (рис. 1).

Рис. 1. Иллюстрация к примеру

Мы видим, что фигуры № 1, 2, 3, 5 - четырехугольники. Каждая из них имеет свое название (рис. 2).

Рис. 2. Четырехугольники

Значит, «лишней» фигурой является треугольник (рис. 3).

Рис. 3. Иллюстрация к примеру

Треугольником называется фигура, которая состоит из трех точек, не лежащих на одной прямой, и трех отрезков, попарно соединяющих эти точки.

Точки называются вершинами треугольника , отрезки - его сторонами . Стороны треугольника образуют в вершинах треугольника три угла.

Основными признаками треугольника являются три стороны и три угла. По величине угла треугольники бывают остроугольные, прямоугольные и тупоугольные.

Треугольник называется остроугольным, если все три угла его острые, то есть меньше 90° (рис. 4).

Рис. 4. Остроугольный треугольник

Треугольник называется прямоугольным, если один из его углов равен 90° (рис. 5).

Рис. 5. Прямоугольный треугольник

Треугольник называется тупоугольным, если один из его углов тупой, то есть больше 90° (рис. 6).

Рис. 6. Тупоугольный треугольник

По числу равных сторон треугольники бывают равносторонние, равнобедренные, разносторонние.

Равнобедренным называется треугольник, у которого две стороны равны (рис. 7).

Рис. 7. Равнобедренный треугольник

Эти стороны называются боковыми , третья сторона - основанием . В равнобедренном треугольнике углы при основании равны.

Равнобедренные треугольники бывают остроугольными и тупоугольными (рис. 8).

Рис. 8. Остроугольный и тупоугольный равнобедренные треугольники

Равносторонним называется треугольник, у которого все три стороны равны (рис. 9).

Рис. 9. Равносторонний треугольник

В равностороннем треугольнике все углы равны . Равносторонние треугольники всегда остроугольные.

Разносторонним называется треугольник, у которого все три стороны имеют разную длину (рис. 10).

Рис. 10. Разносторонний треугольник

Выполните задание. Распределите данные треугольники на три группы (рис. 11).

Рис. 11. Иллюстрация к заданию

Сначала распределим по величине углов.

Остроугольные треугольники: № 1, № 3.

Прямоугольные треугольники: № 2, № 6.

Тупоугольные треугольники: № 4, № 5.

Эти же треугольники распределим на группы по числу равных сторон.

Разносторонние треугольники: № 4, № 6.

Равнобедренные треугольники: № 2, № 3, № 5.

Равносторонний треугольник: № 1.

Рассмотрите рисунки.

Подумайте, из какого куска проволоки сделали каждый треугольник (рис. 12).

Рис. 12. Иллюстрация к заданию

Можно рассуждать так.

Первый кусок проволоки разделен на три равные части, поэтому из него можно сделать равносторонний треугольник. На рисунке он изображен третьим.

Второй кусок проволоки разделен на три разные части, поэтому из него можно сделать разносторонний треугольник. На рисунке он изображен первым.

Третий кусок проволоки разделен на три части, где две части имеют одинаковую длину, значит, из него можно сделать равнобедренный треугольник. На рисунке он изображен вторым.

Сегодня на уроке мы познакомились с различными видами треугольников.

Список литературы

1. М.И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 1. - М.: «Просвещение», 2012.
2. М.И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 2. - М.: «Просвещение», 2012.
3. М.И. Моро. Уроки математики: Методические рекомендации для учителя. 3 класс. - М.: Просвещение, 2012.
4. Нормативно-правовой документ. Контроль и оценка результатов обучения. - М.: «Просвещение», 2011.
5. «Школа России»: Программы для начальной школы. - М.: «Просвещение», 2011.
6. С.И. Волкова. Математика: Проверочные работы. 3 класс. - М.: Просвещение, 2012.
7. В.Н. Рудницкая. Тесты. - М.: «Экзамен», 2012.

1. Nsportal.ru ().
2. Prosv.ru ().
3. Do.gendocs.ru ().

Домашнее задание

1. Закончите фразы.

а) Треугольником называется фигура, которая состоит из …, не лежащих на одной прямой, и …, попарно соединяющих эти точки.

б) Точки называются … , отрезки - его … . Стороны треугольника образуют в вершинах треугольника ….

в) По величине угла треугольники бывают … , … , … .

г) По числу равных сторон треугольники бывают … , … , … .

2. Начертите

а) прямоугольный треугольник;

б) остроугольный треугольник;

в) тупоугольный треугольник;

г) равносторонний треугольник;

д) разносторонний треугольник;

е) равнобедренный треугольник.

3. Составьте задание по теме урока для своих товарищей.