Vektorlar sistemasining chiziqli bog'liqligi. Kollinear vektorlar

Vektor sistemasi deyiladi chiziqli bog'liq, kamida bittasi noldan farq qiladigan raqamlar mavjud bo'lsa, tenglik https://pandia.ru/text/78/624/images/image004_77.gif" width="57" height="24 src=" " >.

Agar bu tenglik faqat hammasi bo'lgan holatda bajarilsa, vektorlar sistemasi deyiladi chiziqli mustaqil.

Teorema. Vektor tizimi bo'ladi chiziqli bog'liq agar uning vektorlaridan kamida bittasi boshqalarning chiziqli birikmasi bo'lsa.

1-misol. Polinom polinomlarning chiziqli birikmasidir https://pandia.ru/text/78/624/images/image010_46.gif" width="88 height=24" height="24">. Polinomlar chiziqli mustaqil tizimni tashkil qiladi, chunki polinom https: //pandia.ru/text/78/624/images/image012_44.gif" width="129" height="24">.

2-misol. Matritsa tizimi, , https://pandia.ru/text/78/624/images/image016_37.gif" width="51" height="48 src="> chiziqli mustaqil, chunki chiziqli birikma tengdir. nol matritsa faqat https://pandia.ru/text/78/624/images/image019_27.gif" width="69" height="21">, , https://pandia.ru/text bo'lganda /78/624 /images/image022_26.gif" width="40" height="21"> chiziqli bog'liq.

Yechim.

Keling, ushbu vektorlarning chiziqli kombinatsiyasini yarataylik https://pandia.ru/text/78/624/images/image023_29.gif" width="97" height="24">=0..gif" width="360" balandlik = "22">.

Teng vektorlarning bir xil koordinatalarini tenglashtirib, biz https://pandia.ru/text/78/624/images/image027_24.gif" width="289" height="69"> ni olamiz.

Nihoyat, olamiz

Va

Tizim noyob trivial yechimga ega, shuning uchun bu vektorlarning chiziqli birikmasi faqat barcha koeffitsientlar nolga teng bo'lganda nolga teng bo'ladi. Shuning uchun bu vektorlar sistemasi chiziqli mustaqildir.

4-misol. Vektorlar chiziqli mustaqildir. Vektor tizimlari qanday bo'ladi?

a).;

b).?

Yechim.

a). Keling, chiziqli birikma yasaymiz va uni nolga tenglashtiramiz

Chiziqli fazoda vektorlar bilan amallar xossalaridan foydalanib, oxirgi tenglikni shaklda qayta yozamiz

Vektorlar chiziqli mustaqil bo'lgani uchun at koeffitsientlari nolga teng bo'lishi kerak, ya'ni.gif" width="12" height="23 src=">

Olingan tenglamalar tizimi o'ziga xos trivial yechimga ega .

Tenglikdan beri (*) faqat https://pandia.ru/text/78/624/images/image031_26.gif" width="115 height=20" height="20"> - chiziqli mustaqil;

b). Keling, tenglikni yarataylik https://pandia.ru/text/78/624/images/image039_17.gif" width="265" height="24 src="> (**)

Shunga o'xshash mulohazalarni qo'llash orqali biz erishamiz

Tenglamalar sistemasini Gauss usuli bilan yechish orqali erishamiz

yoki

Oxirgi tizimda cheksiz ko'p echimlar mavjud https://pandia.ru/text/78/624/images/image044_14.gif" width="149" height="24 src=">. Shunday qilib, bo'lmagan mavjud. tenglikka ega bo'lgan nol koeffitsientlar to'plami (**) . Shuning uchun vektorlar sistemasi - chiziqli bog'liq.

5-misol Vektorlar tizimi chiziqli mustaqil, vektorlar tizimi esa chiziqli bog'liq..gif" width="80" height="24">.gif" width="149 height=24" height="24"> (***)

Tenglikda (***) . Haqiqatan ham, da, tizim chiziqli bog'liq bo'ladi.

Munosabatdan (***) olamiz yoki belgilaylik .

olamiz

uchun vazifalar mustaqil qaror(tomoshabinlarda)

1. Nol vektorni o'z ichiga olgan tizim chiziqli bog'liqdir.

2. Bitta vektordan iborat tizim A, chiziqli bog'liq bo'ladi, agar va faqat, agar, a=0.

3. Ikki vektordan iborat sistema, agar vektorlar proportsional bo'lsa (ya'ni, ulardan biri ikkinchisidan songa ko'paytirilsa) chiziqli bog'liqdir.

4. Agar siz chiziqli bog'liq tizimga vektor qo'shsangiz, siz chiziqli bog'liq tizimga ega bo'lasiz.

5. Agar vektor chiziqli mustaqil tizimdan olib tashlansa, natijada vektorlar tizimi chiziqli mustaqil bo'ladi.

6. Agar tizim S chiziqli mustaqil, lekin vektor qo'shilganda chiziqli bog'liq bo'ladi b, keyin vektor b tizim vektorlari orqali chiziqli ifodalangan S.

c). Ikkinchi tartibli matritsalar fazosida , matritsalar tizimi.

10. Vektorlar sistemasi bo'lsin a,b,c vektor fazo chiziqli mustaqildir. Quyidagi vektor sistemalarning chiziqli mustaqilligini isbotlang:

a).a+b, b, c.

b).a+https://pandia.ru/text/78/624/images/image062_13.gif" width="15" height="19">– ixtiyoriy raqam

c).a+b, a+c, b+c.

11. Mayli a,b,c- uchburchak hosil bo'lishi mumkin bo'lgan tekislikdagi uchta vektor. Bu vektorlar chiziqli bog'liq bo'ladimi?

12. Ikki vektor berilgan a1=(1, 2, 3, 4),a2=(0, 0, 0, 1). Yana ikkita to'rt o'lchovli vektorni toping a3 vaa4 shunday qilib, tizim a1,a2,a3,a4 chiziqli mustaqil edi .

Vektorlar, ularning xossalari va ular bilan harakatlari

Vektorlar, vektorlar bilan amallar, chiziqli vektor fazosi.

Vektorlar cheklangan miqdordagi haqiqiy sonlarning tartiblangan to'plamidir.

Amallar: 1.Vektorni songa ko‘paytirish: lambda*vektor x=(lamda*x 1, lambda*x 2 ... lambda*x n).(3.4, 0, 7)*3=(9, 12,0.21)

2. Vektorlarni qo'shish (bir xil vektor fazoga tegishli) vektor x + vektor y = (x 1 + y 1, x 2 + y 2, ... x n + y n,)

3. Vektor 0=(0,0…0)---n E n – n o‘lchamli (chiziqli fazo) vektor x + vektor 0 = vektor x

Teorema. n ta vektorli sistema, n o'lchovli chiziqli fazo chiziqli bog'liq bo'lishi uchun vektorlardan biri boshqalarning chiziqli birikmasi bo'lishi zarur va etarli.

Teorema. Hodisalarning n o‘lchovli chiziqli fazosining n+ 1-vektorlarining har qanday to‘plami. chiziqli bog'liq.

Vektorlarni qo'shish, vektorlarni raqamlarga ko'paytirish. Vektorlarni ayirish.

Ikki vektor yig'indisi vektorning boshidan oxirigacha yo'naltirilgan vektor bo'lib, boshi vektorning oxiriga to'g'ri keladi. Agar vektorlar bazis birlik vektorlarida kengayishlari bilan berilgan bo'lsa, vektorlarni qo'shganda ularga mos keladigan koordinatalar qo'shiladi.

Keling, buni Dekart koordinata tizimi misolida ko'rib chiqaylik. Mayli

Keling, buni ko'rsataylik

3-rasmdan ko'rinib turibdiki

Har qanday chekli vektorlar yig‘indisini ko‘pburchak qoidasi yordamida topish mumkin (4-rasm): chekli vektorlar yig‘indisini qurish uchun har bir keyingi vektorning boshini oldingisining oxiri bilan birlashtirish kifoya. va birinchi vektorning boshini oxirgi vektorning oxiri bilan bog'lovchi vektorni tuzing.

Vektor qo'shish operatsiyasining xususiyatlari:

Bu ifodalarda m, n sonlardir.

Vektorlar orasidagi farq vektor deyiladi Ikkinchi a'zo - vektorga qarama-qarshi yo'nalish, lekin uzunligi bo'yicha unga teng.

Shunday qilib, vektorlarni ayirish amali qo'shish amali bilan almashtiriladi

Boshlanishi A nuqtada va oxiri A (x1, y1, z1) nuqtada bo'lgan vektor A nuqtaning radius vektori deyiladi va oddiygina belgilanadi. Uning koordinatalari A nuqtaning koordinatalariga to'g'ri kelganligi sababli uning birlik vektorlarda kengayishi ko'rinishga ega.

A(x1, y1, z1) nuqtadan boshlanib, B(x2, y2, z2) nuqtada tugaydigan vektorni quyidagicha yozish mumkin.

bu yerda r 2 B nuqtaning radius vektori; r 1 - A nuqtaning radius vektori.

Shuning uchun birlik vektorlarda vektorning kengayishi shaklga ega

Uning uzunligi A va B nuqtalari orasidagi masofaga teng

KO'PTIRISH

Demak, tekislik masalasida a = (ax; ay) vektorning b soniga ko‘paytmasi formula bo‘yicha topiladi.

a b = (ax b; ay b)

Misol 1. a = (1; 2) vektorining 3 ga ko‘paytmasini toping.

3 a = (3 1; 3 2) = (3; 6)

Demak, fazoviy masalada a = (ax; ay; az) vektorining b soniga ko‘paytmasi formula bo‘yicha topiladi.

a b = (ax b; ay b; az b)

1-misol. a = (1; 2; -5) vektorining 2 ga ko‘paytmasini toping.

2 a = (2 1; 2 2; 2 (-5)) = (2; 4; -10)

Vektorlarning nuqta mahsuloti va vektorlar orasidagi burchak qayerda; bo'lsa, u holda

Skayar mahsulotning ta'rifidan kelib chiqadiki

bu erda, masalan, vektorning vektor yo'nalishi bo'yicha proyeksiyasining kattaligi.

Skalar kvadrat vektor:

Nuqta mahsulotining xususiyatlari:

Koordinatalarda nuqta mahsuloti

Agar Bu

Vektorlar orasidagi burchak

Vektorlar orasidagi burchak - bu vektorlarning yo'nalishlari orasidagi burchak (eng kichik burchak).

O'zaro mahsulot (Ikki vektorning o'zaro mahsuloti.) - bu ikki omildan tuzilgan tekislikka perpendikulyar bo'lgan psevdovektor bo'lib, bu uch o'lchovli Evklid fazosida vektorlar ustidan "vektorlarni ko'paytirish" ikkilik operatsiyasining natijasidir. Mahsulot kommutativ ham, assotsiativ ham emas (u antikommutativ) va vektorlarning nuqta mahsulotidan farq qiladi. Ko'pgina muhandislik va fizika muammolarida siz ikkita mavjudga perpendikulyar vektorni qurishingiz kerak - vektor mahsuloti bu imkoniyatni beradi. Xoch mahsulot vektorlarning perpendikulyarligini "o'lchash" uchun foydalidir - uzunlik vektor mahsuloti ikkita vektor, agar ular perpendikulyar bo'lsa, ularning uzunliklari ko'paytmasiga teng va vektorlar parallel yoki antiparallel bo'lsa, nolga kamayadi.

O'zaro mahsulot faqat uch o'lchovli va etti o'lchovli bo'shliqlarda aniqlanadi. Vektor mahsulotining natijasi, xuddi skalar mahsulot kabi, Evklid fazosining metrikasiga bog'liq.

Uch o'lchovli to'rtburchaklar koordinatalar tizimidagi koordinatalardan skalyar mahsulot vektorlarini hisoblash formulasidan farqli o'laroq, o'zaro mahsulot formulasi to'rtburchaklar koordinatalar tizimining yo'nalishiga yoki boshqacha aytganda, uning "xiralligiga" bog'liq.

Vektorlarning kollinearligi.

Ikki nolga teng bo'lmagan (0 ga teng bo'lmagan) vektorlar, agar ular parallel to'g'rilar ustida yoki bir xil to'g'rida yotsa, ular kollinear deyiladi. Qabul qilinadigan, lekin tavsiya etilmaydigan sinonim "parallel" vektorlardir. Kollinear vektorlar bir xil yo'naltirilgan ("ko'p yo'nalishli") yoki qarama-qarshi yo'naltirilgan bo'lishi mumkin (ikkinchi holatda ular ba'zan "antikollinear" yoki "antiparallel" deb ataladi).

Vektorlarning aralash mahsuloti ( a, b, c)- a vektorning skalyar ko'paytmasi va b va c vektorlarning vektor ko'paytmasi:

(a,b,c)=a ⋅(b ×c)

ba'zan uchlik deb ataladi skalyar mahsulot vektorlar, ehtimol, natija skaler (aniqrog'i, psevdoskalar) ekanligi bilan bog'liq.

Geometrik ma'no: Aralashtirilgan mahsulotning moduli son jihatdan vektorlar hosil qilgan parallelepiped hajmiga teng. (a,b,c) .

Xususiyatlari

Aralash bo'lak uning barcha argumentlariga nisbatan skew-simmetrik: ya'ni. e. har qanday ikkita omilni qayta tartibga solish mahsulotning belgisini o'zgartiradi. Bundan kelib chiqadiki, o'ng dekart koordinata tizimidagi Aralash mahsulot (ortonormal asosda) vektorlardan tashkil topgan matritsaning determinantiga teng va:

Chap kartezian koordinata tizimidagi aralash mahsulot (ortonormal asosda) vektorlardan tashkil topgan matritsaning determinantiga teng va minus belgisi bilan olinadi:

Ayniqsa,

Agar ikkita vektor parallel bo'lsa, u holda har qanday uchinchi vektor bilan ular nolga teng aralash mahsulot hosil qiladi.

Agar uchta vektor chiziqli bog'liq bo'lsa (ya'ni, koplanar, bir tekislikda yotsa), unda ularning aralash mahsuloti nolga teng.

Geometrik ma'no - Aralash mahsulot mutlaq qiymatda vektorlar tomonidan hosil qilingan parallelepiped (rasmga qarang) hajmiga teng va; belgi vektorlarning bu uchligi o'ng yoki chap qo'l ekanligiga bog'liq.

Vektorlarning mutanosibligi.

Uch vektor (yoki kattaroq raqam) koplanar deyiladi, agar ular umumiy kelib chiqishiga keltirilib, bir tekislikda yotsa

Tegishlilik xossalari

Agar uchta vektordan kamida bittasi nolga teng bo'lsa, u holda uchta vektor ham koplanar hisoblanadi.

Bir juft kollinear vektorni o'z ichiga olgan uchlik vektorlar koplanardir.

Koplanar vektorlarning aralash mahsuloti. Bu uchta vektorning mutanosibligi uchun mezondir.

Koplanar vektorlar chiziqli bog'liqdir. Bu ham mutanosiblik mezoni hisoblanadi.

3 o'lchovli fazoda 3 ta tekis bo'lmagan vektor asosni tashkil qiladi

Chiziqli bog'liq va chiziqli mustaqil vektorlar.

Chiziqli qaram va mustaqil vektor sistemalar.Ta'rif. Vektor sistemasi deyiladi chiziqli bog'liq, agar bu vektorlarning nol vektoriga teng bo'lgan kamida bitta noan'anaviy chiziqli birikmasi mavjud bo'lsa. Aks holda, ya'ni. agar berilgan vektorlarning faqat arzimas chiziqli birikmasi nol vektorga teng bo'lsa, vektorlar deyiladi chiziqli mustaqil.

Teorema (chiziqli bog'liqlik mezoni). Chiziqli fazodagi vektorlar sistemasi chiziqli bog'liq bo'lishi uchun bu vektorlardan kamida bittasi boshqalarning chiziqli birikmasi bo'lishi zarur va etarli.

1) Agar vektorlar orasida kamida bitta nol vektor bo'lsa, u holda vektorlarning butun tizimi chiziqli bog'liqdir.

Darhaqiqat, agar, masalan, , deb faraz qilsak, bizda notrivial chiziqli birikma mavjud.▲

2) Agar vektorlar orasidan ba'zilari chiziqli bog'liq tizimni tashkil qilsa, u holda butun tizim chiziqli bog'liqdir.

Haqiqatan ham, , , vektorlari chiziqli bog'liq bo'lsin. Bu nol vektorga teng bo'lmagan trivial chiziqli birikma mavjudligini anglatadi. Ammo keyin, taxmin qilish , biz nol vektorga teng bo'lmagan notrivial chiziqli birikmani ham olamiz.

2. Asos va o‘lcham. Ta'rif. Chiziqli mustaqil vektorlar tizimi vektor fazosi deyiladi asos bu fazoning har qanday vektori ushbu tizim vektorlarining chiziqli birikmasi sifatida ifodalanishi mumkin bo'lsa, ya'ni. Har bir vektor uchun haqiqiy sonlar mavjud tenglik shunday bo'ladiki, bu tenglik deyiladi vektor parchalanishi asos va raqamlarga ko'ra chaqiriladi vektorning bazisga nisbatan koordinatalari(yoki asosda) .

Teorema (asosiyga nisbatan kengayishning o'ziga xosligi to'g'risida). Kosmosdagi har bir vektor bazaga kengaytirilishi mumkin yagona yo'l bilan, ya'ni. asosdagi har bir vektorning koordinatalari aniq belgilanadi.

Vektorlar tizimining chiziqli bog'liqligini tekshirish uchun ushbu vektorlarning chiziqli birikmasini tuzish va kamida bitta koeffitsient nolga teng bo'lsa, u nolga teng bo'lishi mumkinligini tekshirish kerak.

1-holat. Vektorlar sistemasi vektorlar orqali berilgan

Chiziqli kombinatsiyani yaratish

Biz bir hil tenglamalar tizimini oldik. Agar u nolga teng bo'lmagan yechimga ega bo'lsa, determinant nolga teng bo'lishi kerak. Determinant tuzamiz va uning qiymatini topamiz.

Determinant nolga teng, shuning uchun vektorlar chiziqli bog'liqdir.

2-holat. Vektorlar sistemasi analitik funksiyalar bilan aniqlanadi:

a)
, agar identifikatsiya rost bo'lsa, u holda tizim chiziqli bog'liqdir.

Keling, chiziqli birikma yasaymiz.

Bu ifoda nolga teng bo'lgan a, b, c (hech bo'lmaganda bittasi nolga teng bo'lmagan) mavjudligini tekshirish kerak.

Giperbolik funksiyalarni yozamiz

,
, Keyin

u holda vektorlarning chiziqli birikmasi quyidagi shaklni oladi:

Qayerda
, masalan, chiziqli birikma nolga teng, shuning uchun tizim chiziqli bog'liqdir.

Javob: tizim chiziqli bog'liq.

b)
, chiziqli birikma yasaymiz

X ning har qanday qiymatlari uchun vektorlarning chiziqli birikmasi nolga teng bo'lishi kerak.

Keling, alohida holatlar mavjudligini tekshirib ko'ramiz.

Vektorlarning chiziqli birikmasi faqat barcha koeffitsientlar nolga teng bo'lsa, nolga teng.

Shuning uchun tizim chiziqli mustaqildir.

Javob: tizim chiziqli mustaqil.

5.3. Bazis toping va chiziqli yechim fazosining o‘lchamini aniqlang.

Kengaytirilgan matritsa hosil qilamiz va uni Gauss usulida trapetsiya shakliga keltiramiz.

Ba'zi asoslarni olish uchun ixtiyoriy qiymatlarni almashtiramiz:

Keling, qolgan koordinatalarni olamiz

Javob:

5.4. X vektorning bazisdagi koordinatalarini toping, agar u bazisda berilgan bo'lsa.

Vektorning koordinatalarini yangi asosda topish tenglamalar tizimini yechishga keltiriladi

1-usul. O'tish matritsasi yordamida topish

Keling, o'tish matritsasini yarataylik

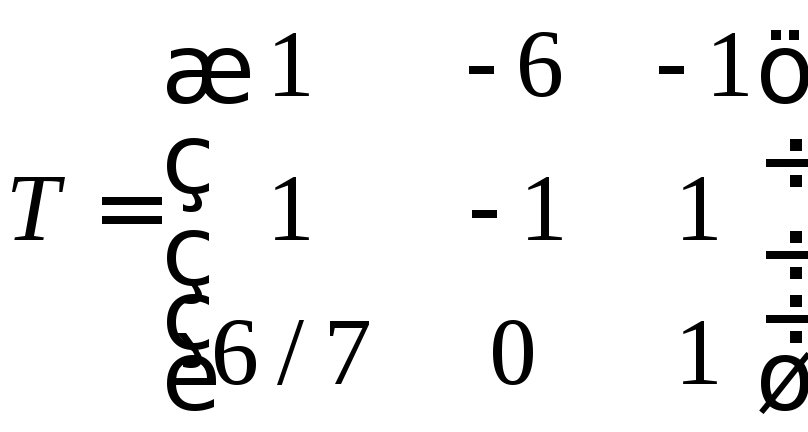
Yangi asosdagi vektorni formuladan foydalanib topamiz

Teskari matritsani topamiz va ko'paytirishni bajaramiz

,

2-usul. Tenglamalar sistemasini tuzish orqali topish.

Bazis koeffitsientlaridan bazis vektorlarini tuzamiz

,
,

Yangi asosda vektorni topish ko'rinishga ega

, Qayerda d bu berilgan vektor x.

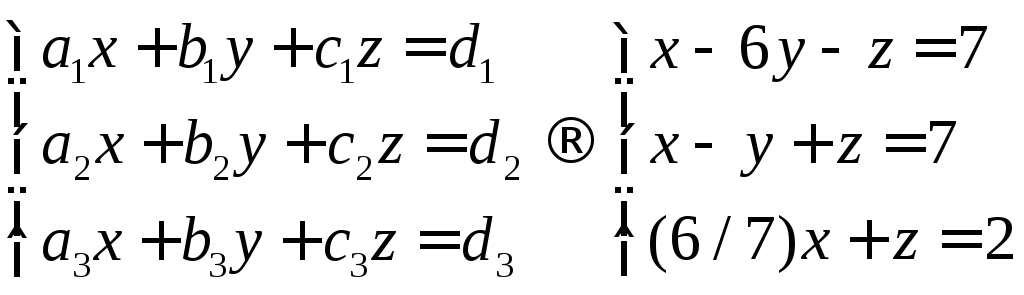
Olingan tenglamani har qanday usulda echish mumkin, javob o'xshash bo'ladi.

Javob: vektor yangi asosda
.

5.5. x = bo'lsin (x 1 , x 2 , x 3 ) . Quyidagi o'zgarishlar chiziqlimi?

Berilgan vektorlarning koeffitsientlaridan chiziqli operatorlar matritsalarini tuzamiz.

Har bir chiziqli operator matritsasi uchun chiziqli amallar xossasini tekshirib ko'ramiz.

Matritsani ko'paytirish orqali chap tomonni topamiz A vektorga

Berilgan vektorni skalerga ko'paytirish orqali o'ng tomonni topamiz
.

Biz buni ko'ramiz
Bu transformatsiya chiziqli emasligini anglatadi.

Keling, boshqa vektorlarni ko'rib chiqaylik.

, transformatsiya chiziqli emas.

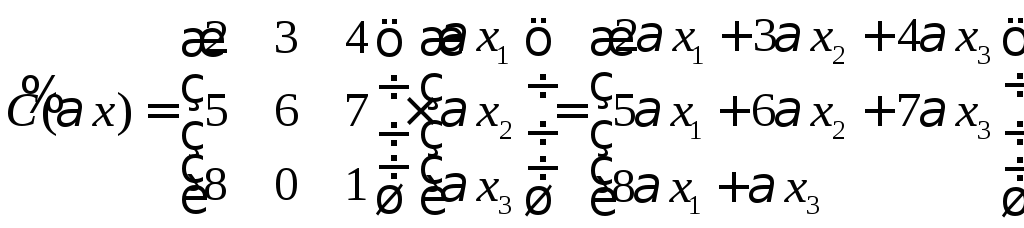
, transformatsiya chiziqli.

Javob: Oh- chiziqli transformatsiya emas, In- chiziqli emas, Cx- chiziqli.

Eslatma. Berilgan vektorlarga diqqat bilan qarab, bu vazifani ancha oson bajarishingiz mumkin. IN Oh elementlardan iborat bo‘lmagan atamalar mavjudligini ko‘ramiz X, bu chiziqli operatsiya natijasida olinishi mumkin emas edi. IN In element mavjud X uchinchi darajaga, uni vektorga ko'paytirish orqali ham olish mumkin emas X.

5.6. Berilgan x = { x 1 , x 2 , x 3 } , Ax = { x 2 – x 3 , x 1 , x 1 + x 3 } , Bx = { x 2 , 2 x 3 , x 1 } . Belgilangan operatsiyani bajaring: ( A ( B – A )) x .

Chiziqli operatorlarning matritsalarini yozamiz.

Matritsalar ustida amal bajaramiz

Olingan matritsani X ga ko'paytirganda, biz olamiz

Javob:

Ushbu maqolada biz quyidagilarni ko'rib chiqamiz:

• kollinear vektorlar nima;
• vektorlarning kollinearligi uchun qanday shartlar mavjud;
• kollinear vektorlarning qanday xossalari mavjudligi;
• kollinear vektorlarning chiziqli bog'liqligi nima.

Yandex.RTB R-A-339285-1 Ta'rif 1

Kollinear vektorlar bir chiziqqa parallel yoki bir chiziqda yotuvchi vektorlardir.

1-misol

Vektorlarning kollinearligi shartlari

Quyidagi shartlardan biri to‘g‘ri bo‘lsa, ikkita vektor kollinear hisoblanadi:

• shart 1 . a va b vektorlar, agar a = l b bo'lgan l soni bo'lsa, kollinear;
• shart 2 . a va b vektorlari teng koordinata nisbatlari bilan kollineardir:

a = (a 1 ; a 2) , b = (b 1 ; b 2) ⇒ a ∥ b ⇔ a 1 b 1 = a 2 b 2

• shart 3 . a va b vektorlari o'zaro ko'paytma va nol vektor teng bo'lsa, kollinear bo'ladi:

a ∥ b ⇔ a , b = 0

Eslatma 1

2-shart vektor koordinatalaridan biri nolga teng bo'lsa, qo'llanilmaydi.

Eslatma 2

3-shart faqat fazoda ko'rsatilgan vektorlarga nisbatan qo'llaniladi.

Vektorlarning kollinearligini o'rganish masalalariga misollar

1-misol

a = (1; 3) va b = (2; 1) vektorlarini kollinearlik uchun tekshiramiz.

Qanday hal qilish kerak?

IN Ushbu holatda 2-kollinearlik shartidan foydalanish kerak. Berilgan vektorlar uchun u quyidagicha ko'rinadi:

Tenglik noto'g'ri. Bundan a va b vektorlar kollinear emas degan xulosaga kelishimiz mumkin.

Javob : a | | b

2-misol

Vektorlar kollinear bo'lishi uchun a = (1; 2) va b = (- 1; m) vektorning qanday m qiymati kerak?

Qanday hal qilish kerak?

Ikkinchi kollinearlik shartidan foydalanib, vektorlar, agar ularning koordinatalari proportsional bo'lsa, kollinear bo'ladi:

Bu m = - 2 ekanligini ko'rsatadi.

Javob: m = - 2.

Vektor sistemalarning chiziqli bog`liqligi va chiziqli mustaqilligi mezonlari

Teorema

Vektor fazodagi vektorlar sistemasi sistema vektorlaridan biri shu sistemaning qolgan vektorlari bilan ifodalanishi mumkin bo'lgan taqdirdagina chiziqli bog'liq bo'ladi.

Isbot

Sistema e 1, e 2, bo'lsin. . . , e n chiziqli bog'liqdir. Bu sistemaning nol vektoriga teng chiziqli birikmasini yozamiz:

a 1 e 1 + a 2 e 2 +. . . + a n e n = 0

unda kombinatsiya koeffitsientlarining kamida bittasi nolga teng emas.

a k ≠ 0 k ∈ 1, 2, bo'lsin. . . , n.

Tenglikning ikkala tomonini nolga teng bo'lmagan koeffitsientga ajratamiz:

a k - 1 (a k - 1 a 1) e 1 + (a k - 1 a k) e k + . . . + (a k - 1 a n) e n = 0

Belgilaymiz:

A k - 1 a m, bu erda m ∈ 1, 2,. . . , k - 1, k + 1, n

Unday bo `lsa:

b 1 e 1 + . . . + b k - 1 e k - 1 + b k + 1 e k + 1 +. . . + b n e n = 0

yoki e k = (- b 1) e 1 + . . . + (- b k - 1) e k - 1 + (- b k + 1) e k + 1 + . . . + (- b n) e n

Bundan kelib chiqadiki, tizim vektorlaridan biri tizimning barcha boshqa vektorlari orqali ifodalanadi. Qaysi narsa isbotlanishi kerak edi (va hokazo).

Adekvatlik

Vektorlardan biri tizimning barcha boshqa vektorlari orqali chiziqli ifodalansin:

e k = g 1 e 1 +. . . + g k - 1 e k - 1 + g k + 1 e k + 1 +. . . + g n e n

e k vektorini ushbu tenglikning o'ng tomoniga o'tkazamiz:

0 = g 1 e 1 +. . . + g k - 1 e k - 1 - e k + g k + 1 e k + 1 +. . . + g n e n

e k vektorining koeffitsienti - 1 ≠ 0 ga teng bo'lgani uchun e 1, e 2, vektorlar sistemasi orqali nolning notrivial tasvirini olamiz. . . , e n va bu, o'z navbatida, bu vektorlar tizimi chiziqli bog'liqligini bildiradi. Qaysi narsa isbotlanishi kerak edi (va hokazo).

Natija:

• Vektorlar tizimi chiziqli mustaqil hisoblanadi, agar uning vektorlaridan hech biri tizimning boshqa barcha vektorlari bilan ifodalana olmasa.
• Nol vektor yoki ikkita teng vektorni o'z ichiga olgan vektorlar tizimi chiziqli bog'liqdir.

Chiziqli bog'liq vektorlarning xossalari

1. 2 va 3 o'lchovli vektorlar uchun quyidagi shart bajariladi: ikkita chiziqli bog'liq vektor kollineardir. Ikki kollinear vektor chiziqli bog'liqdir.
2. 3 o'lchovli vektorlar uchun shart bajariladi: uchta chiziqli bog'liq vektorlar- koplanar. (3 koplanar vektor chiziqli bog'liq).
3. n o'lchovli vektorlar uchun quyidagi shart bajariladi: n + 1 vektorlar doimo chiziqli bog'liqdir.

Vektorlarning chiziqli bog'liqligi yoki chiziqli mustaqilligi bilan bog'liq masalalarni yechish misollari

3-misol

a = 3, 4, 5, b = - 3, 0, 5, c = 4, 4, 4, d = 3, 4, 0 vektorlarining chiziqli mustaqilligini tekshiramiz.

Yechim. Vektorlar chiziqli bog'liqdir, chunki vektorlarning o'lchamlari vektorlar sonidan kamroq.

4-misol

a = 1, 1, 1, b = 1, 2, 0, c = 0, - 1, 1 vektorlarining chiziqli mustaqilligini tekshiramiz.

Yechim. Biz chiziqli birikma nol vektorga teng bo'lgan koeffitsientlarning qiymatlarini topamiz:

x 1 a + x 2 b + x 3 c 1 = 0

Vektor tenglamani chiziqli shaklda yozamiz:

x 1 + x 2 = 0 x 1 + 2 x 2 - x 3 = 0 x 1 + x 3 = 0

Ushbu tizimni Gauss usuli yordamida hal qilamiz:

1 1 0 | 0 1 2 - 1 | 0 1 0 1 | 0 ~

2-qatordan biz 1-ni, 3-chidan 1-ni ayiramiz:

~ 1 1 0 | 0 1 - 1 2 - 1 - 1 - 0 | 0 - 0 1 - 1 0 - 1 1 - 0 | 0 - 0 ~ 1 1 0 | 0 0 1 - 1 | 0 0 - 1 1 | 0 ~

1-qatordan 2-ni ayirib, 3-chi qatorga 2-ni qoʻshamiz:

~ 1 - 0 1 - 1 0 - (- 1) | 0 - 0 0 1 - 1 | 0 0 + 0 - 1 + 1 1 + (- 1) | 0 + 0 ~ 0 1 0 | 1 0 1 - 1 | 0 0 0 0 | 0

Yechimdan kelib chiqadiki, tizim ko'plab echimlarga ega. Bu shuni anglatadiki, x 1, x 2, x 3 raqamlari qiymatlarining nolga teng bo'lmagan kombinatsiyasi mavjud bo'lib, ular uchun a, b, c ning chiziqli birikmasi nol vektorga teng. Shuning uchun a, b, c vektorlari chiziqli bog'liq.

Agar siz matnda xatolikni sezsangiz, uni belgilang va Ctrl+Enter tugmalarini bosing

a 1 = { 3, 5, 1 , 4 }, a 2 = { –2, 1, -5 , -7 }, a 3 = { -1, –2, 0, –1 }.

Yechim. qidirmoqdalar umumiy qaror tenglamalar tizimlari

a 1 x 1 + a 2 x 2 + a 3 x 3 = Θ

Gauss usuli. Buning uchun biz ushbu bir hil tizimni koordinatalarda yozamiz:

Tizim matritsasi

Ruxsat etilgan tizim quyidagi shaklga ega: (r A = 2, n= 3). Tizim kooperativ va noaniq. Uning umumiy yechimi ( x 2 - erkin o'zgaruvchi): x 3 = 13x 2 ; 3x 1 – 2x 2 – 13x 2 = 0 => x 1 = 5x 2 => X o =. Masalan, nolga teng bo'lmagan xususiy yechimning mavjudligi vektorlar ekanligini ko'rsatadi a 1 , a 2 , a 3 chiziqli bog'liq.

2-misol.

Berilgan vektorlar sistemasi chiziqli bog'liqmi yoki chiziqli mustaqil ekanligini aniqlang:

1. a 1 = { -20, -15, - 4 }, a 2 = { –7, -2, -4 }, a 3 = { 3, –1, –2 }.

Yechim. Bir jinsli tenglamalar tizimini ko'rib chiqaylik a 1 x 1 + a 2 x 2 + a 3 x 3 = Θ

yoki kengaytirilgan shaklda (koordinatalar bo'yicha)

Tizim bir hil. Agar u degeneratsiyalanmagan bo'lsa, unda bor yagona qaror. Bir hil tizimda nol (arzimas) yechim mavjud. Bu shuni anglatadiki, bu holda vektorlar tizimi mustaqildir. Agar tizim buzilgan bo'lsa, u nolga teng bo'lmagan echimlarga ega va shuning uchun u bog'liqdir.

Biz tizimni degeneratsiya uchun tekshiramiz:

= –80 – 28 + 180 – 48 + 80 – 210 = – 106 ≠ 0.

Tizim degenerativ emas va shuning uchun vektorlar a 1 , a 2 , a 3 chiziqli mustaqil.

Vazifalar. Berilgan vektorlar sistemasi chiziqli bog'liqmi yoki chiziqli mustaqil ekanligini aniqlang:

1. a 1 = { -4, 2, 8 }, a 2 = { 14, -7, -28 }.

2. a 1 = { 2, -1, 3, 5 }, a 2 = { 6, -3, 3, 15 }.

3. a 1 = { -7, 5, 19 }, a 2 = { -5, 7 , -7 }, a 3 = { -8, 7, 14 }.

4. a 1 = { 1, 2, -2 }, a 2 = { 0, -1, 4 }, a 3 = { 2, -3, 3 }.

5. a 1 = { 1, 8 , -1 }, a 2 = { -2, 3, 3 }, a 3 = { 4, -11, 9 }.

6. a 1 = { 1, 2 , 3 }, a 2 = { 2, -1 , 1 }, a 3 = { 1, 3, 4 }.

7. a 1 = {0, 1, 1 , 0}, a 2 = {1, 1 , 3, 1}, a 3 = {1, 3, 5, 1}, a 4 = {0, 1, 1, -2}.

8. a 1 = {-1, 7, 1 , -2}, a 2 = {2, 3 , 2, 1}, a 3 = {4, 4, 4, -3}, a 4 = {1, 6, -11, 1}.

9. Vektorlar sistemasi chiziqli bog‘liq bo‘lishini isbotlang, agar u quyidagilardan iborat bo‘lsa:

a) ikkita teng vektor;

b) ikkita proportsional vektor.