В нашем повседневном опыте слово «работа» встречается очень часто. Но следует различать работу физиологическую и работу с точки зрения науки физики. Когда вы приходите с уроков, вы говорите: «Ой, как я устал!». Это работа физиологическая. Или, к примеру, работа коллектива в народной сказке «Репка».
Рис 1. Работа в повседневном смысле слова
Мы же будем говорить здесь о работе с точки зрения физики.
Механическая работа совершается, если под действием силы происходит перемещение тела. Работа обозначается латинской буквой А. Более строго определение работы звучит так.
Работой силы называется физическая величина, равная произведению величины силы на расстояние, пройденное телом в направлении действия силы.
Рис 2. Работа — это физическая величина
Формула справедлива, когда на тело действует постоянная сила.
В международной системе единиц СИ работа измеряется в джоулях.
Это означает, что если под действием силы в 1 ньютон тело переместилось на 1 метр, то данной силой совершена работа 1 джоуль.
Единица работы названа в честь английского ученого Джеймса Прескотта Джоуля.
Рис 3. Джеймс Прескотт Джоуль (1818 — 1889)
Из формулы для вычисления работы следует, что возможны три случая, когда работа равна нулю.
Первый случай — когда на тело действует сила, но тело не перемещается. Например, на дом действует огромная сила тяжести. Но она не совершает работы, поскольку дом неподвижен.
Второй случай — когда тело перемещается по инерции, то есть на него не действуют никакие силы. Например, космический корабль движется в межгалактическом пространстве.
Третий случай — когда на тело действует сила, перпендикулярная направлению движения тела. В этом случае, хотя и тело перемещается, и сила на него действует, но нет перемещения тела в направлении действия силы.
Рис 4. Три случая, когда работа равна нулю
Следует также сказать, что работа силы может быть отрицательной. Так будет, если перемещение тела происходит против направления действия силы. Например, когда подъемный кран с помощью троса поднимает груз над землей, работа силы тяжести отрицательна (а работа силы упругости троса, направленная вверх, наоборот, положительна).
Предположим, при выполнении строительных работ котлован необходимо засыпать песком. Экскаватору для этого понадобится несколько минут, а рабочему с помощью лопаты пришлось бы трудиться несколько часов. Но и экскаватор, и рабочий при этом выполнили бы одну и ту же работу.
Рис 5. Одну и ту же работу можно выполнить за разное время
Чтобы охарактеризовать быстроту выполнения работы в физике используется величина, называемая мощностью.
Мощностью называется физическая величина, равная отношению работы ко времени ее выполнения.
Мощность обозначается латинской буквой N.
Единицей измерения мощности я системе СИ является ватт.
Один ватт — это мощность, при которой работа в один джоуль совершается за одну секунду.
Единица мощности названа в честь английского ученого, изобретателя паровой машины Джеймса Уатта.
Рис 6. Джеймс Уатт (1736 — 1819)
Объединим формулу для вычисления работы с формулой для вычисления мощности.
Вспомним теперь, что отношение пути, пройденного телом, S, ко времени движения t представляет собой скорость движения тела v.
Таким образом, мощность равна произведению численного значения силы на скорость движения тела в направлении действия силы.
Этой формулой удобно пользоваться при решении задач, в которых сила действует на тело, движущееся с известной скоростью.
Список литературы
- Лукашик В.И., Иванова Е.В. Сборник задач по физике для 7-9 классов общеобразовательных учреждений. — 17-е изд. — М.: Просвещение, 2004.
- Перышкин А.В. Физика. 7 кл. — 14-е изд., стереотип. — М.: Дрофа, 2010.
- Перышкин А.В. Сборник задач по физике, 7-9 кл.: 5-е изд., стереотип. — М: Издательство «Экзамен», 2010.
- Интернет-портал Physics.ru ().
- Интернет-портал Festival.1september.ru ().
- Интернет-портал Fizportal.ru ().
- Интернет-портал Elkin52.narod.ru ().
Домашнее задание
- В каких случаях работа равна нулю?
- Как находится работа на пути, пройденном в направлении действия силы? В противоположном направлении?
- Какую работу совершает сила трения, действующая на кирпич, при его перемещении на 0,4 м? Сила трения равна 5 Н.
Если на телодействует сила, то эта сила совершаетработу по перемещению этого тела. Преждечем дать определение работе прикриволинейном движении материальнойточки, рассмотрим частные случаи:
В этом случаемеханическая работа Aравна:
A=F s cos
=
,
или A= Fcos
×s = F S ×s ,
гдеF S – проекциясилы
на перемещение. В данном случаеF s =const,и геометрический смысл работы A– это площадь прямоугольника,построенного в координатах F S ,,s.
Построим графикпроекции силы на направление перемещенияF Sкак функции перемещения s.Полное перемещение представим как суммуnмалых перемещений
.Для малого i-огоперемещения
работа равна
или площади заштрихованной трапециина рисунке.
Полнаямеханическая работа по перемещению източки 1в точку 2будет равна:
.
Величина, стоящаяпод интегралом будет представлятьэлементарную работу по бесконечномалому перемещению
:
– элементарная работа.
Разбиваемтраекторию движения материальной точкина бесконечно малые перемещения
и работу силы
по перемещению материальной точки източки 1в точку 2определяем как криволинейный интеграл:
–работа прикриволинейном движении.
Пример 1:Работасилы тяжести
при криволинейном движении материальнойточки.
.
Далее
как постоянную величину можно вынестиза знак интеграла, а интеграл
согласнорисунку будет представлять полноеперемещение
..
Если обозначитьвысоту точки 1от поверхности Земли через
,а высоту точки 2через
,то
Мы видим, что вданном случае работа определяетсяположением материальной точки в начальныйи конечный момент времени и не зависитот формы траектории или пути. Работасилы тяжести по замкнутому пути равнанулю:
.
Силы, работакоторых на замкнутом пути равна нулю,называетсяконсервативными.
Пример 2: Работа силы трения.
Это примернеконсервативной силы. Чтобы показатьэто достаточно рассмотреть элементарнуюработу силы трения:
,
т.е. работа силытрения всегда отрицательная величинаи на замкнутом пути не может быть равнойнулю. Работа, совершаемая в единицувремени, называется мощностью.Если за время
совершается работа
,то мощность равна
–механическаямощность.
Взяв
в виде
,
получим длямощности выражение:
.
В СИ единицейработы является джоуль:
=1 Дж = 1 Н
1м, а единицей мощности является ватт: 1Вт = 1 Дж/с.
Механическая энергия.
Энергия являетсяобщей количественной мерой движениявзаимодействия всех видов материи.Энергия не исчезает и не возникает изнечего: она лишь может переходить изодной формы в другую. Понятие энергиисвязывает воедино все явления в природе.В соответствии с различными формамидвижения материи рассматривают разныевиды энергии – механическую, внутреннюю,электромагнитную, ядерную и др.
Понятия энергиии работы тесно связаны друг с другом.Известно, что работа совершается засчет запаса энергии и, наоборот, совершаяработу, можно увеличить запас энергиив каком-либо устройстве. Другими словамиработа – это количественная мераизменения энергии:
.
Энергия также каки работа в СИ измеряется в джоулях: [E]=1Дж.
Механическаяэнергия бывает двух видов – кинетическаяи потенциальная.
Кинетическаяэнергия(или энергиядвижения) определяется массами искоростями рассматриваемых тел.Рассмотрим материальную точку, движущуюсяпод действием силы
.Работа этой силы увеличивает кинетическуюэнергию материальной точки
.Вычислим в этом случае малое приращение(дифференциал) кинетической энергии:
При вычислении
использованвторой закон Ньютона
,а также
— модуль скорости материальной точки.Тогда
можно представить в виде:
—
— кинетическаяэнергия движущейся материальной точки.
Умножив и разделивэто выражение на
,и учитывая, что
,получим
—
— связьмежду импульсом и кинетической энергиейдвижущейся материальной точки.
Потенциальнаяэнергия(илиэнергия положения тел) определяетсядействием на тело консервативных сили зависит только от положения тела.
Мы видели, чтоработу силы тяжести
при криволинейном движении материальнойточки
можно представить в виде разностизначений функции
,взятых в точке 1и в точке2:
.
Оказывается, чтовсегда, когда силы консервативны, работуэтих сил на пути 1
2можно представить в виде:
.
Функция
,котораязависит только от положения тела –называется потенциальной энергией.
Тогда дляэлементарной работы получим
–работа равнаубыли потенциальной энергии.
Иначе можносказать, что работа совершается за счётзапаса потенциальной энергии.
Величину
,равную сумме кинетической и потенциальнойэнергий частицы, называют полноймеханической энергией тела:
–полнаямеханическая энергия тела.
В заключениизаметим, что используя второй законНьютона
,дифференциал кинетической энергии
можно представить в виде:
.
Дифференциалпотенциальной энергии
,как указывали выше, равен:
.
Таким образом,если сила
– консервативная сила и отсутствуютдругие внешние силы, то
,т.е. в этом случае полная механическаяэнергия тела сохраняется.
В нашем повседневном опыте слово «работа» встречается очень часто. Но следует различать работу физиологическую и работу с точки зрения науки физики. Когда вы приходите с уроков, вы говорите: «Ой, как я устал!». Это работа физиологическая. Или, к примеру, работа коллектива в народной сказке «Репка».
Рис 1. Работа в повседневном смысле слова
Мы же будем говорить здесь о работе с точки зрения физики.
Механическая работа совершается, если под действием силы происходит перемещение тела. Работа обозначается латинской буквой А. Более строго определение работы звучит так.
Работой силы называется физическая величина, равная произведению величины силы на расстояние, пройденное телом в направлении действия силы.
Рис 2. Работа — это физическая величина
Формула справедлива, когда на тело действует постоянная сила.
В международной системе единиц СИ работа измеряется в джоулях.
Это означает, что если под действием силы в 1 ньютон тело переместилось на 1 метр, то данной силой совершена работа 1 джоуль.
Единица работы названа в честь английского ученого Джеймса Прескотта Джоуля.
Рис 3. Джеймс Прескотт Джоуль (1818 — 1889)
Из формулы для вычисления работы следует, что возможны три случая, когда работа равна нулю.
Первый случай — когда на тело действует сила, но тело не перемещается. Например, на дом действует огромная сила тяжести. Но она не совершает работы, поскольку дом неподвижен.
Второй случай — когда тело перемещается по инерции, то есть на него не действуют никакие силы. Например, космический корабль движется в межгалактическом пространстве.
Третий случай — когда на тело действует сила, перпендикулярная направлению движения тела. В этом случае, хотя и тело перемещается, и сила на него действует, но нет перемещения тела в направлении действия силы.
Рис 4. Три случая, когда работа равна нулю
Следует также сказать, что работа силы может быть отрицательной. Так будет, если перемещение тела происходит против направления действия силы. Например, когда подъемный кран с помощью троса поднимает груз над землей, работа силы тяжести отрицательна (а работа силы упругости троса, направленная вверх, наоборот, положительна).
Предположим, при выполнении строительных работ котлован необходимо засыпать песком. Экскаватору для этого понадобится несколько минут, а рабочему с помощью лопаты пришлось бы трудиться несколько часов. Но и экскаватор, и рабочий при этом выполнили бы одну и ту же работу.
Рис 5. Одну и ту же работу можно выполнить за разное время
Чтобы охарактеризовать быстроту выполнения работы в физике используется величина, называемая мощностью.
Мощностью называется физическая величина, равная отношению работы ко времени ее выполнения.
Мощность обозначается латинской буквой N.
Единицей измерения мощности я системе СИ является ватт.
Один ватт — это мощность, при которой работа в один джоуль совершается за одну секунду.
Единица мощности названа в честь английского ученого, изобретателя паровой машины Джеймса Уатта.
Рис 6. Джеймс Уатт (1736 — 1819)
Объединим формулу для вычисления работы с формулой для вычисления мощности.
Вспомним теперь, что отношение пути, пройденного телом, S, ко времени движения t представляет собой скорость движения тела v.
Таким образом, мощность равна произведению численного значения силы на скорость движения тела в направлении действия силы.
Этой формулой удобно пользоваться при решении задач, в которых сила действует на тело, движущееся с известной скоростью.
Список литературы
- Лукашик В.И., Иванова Е.В. Сборник задач по физике для 7-9 классов общеобразовательных учреждений. — 17-е изд. — М.: Просвещение, 2004.
- Перышкин А.В. Физика. 7 кл. — 14-е изд., стереотип. — М.: Дрофа, 2010.
- Перышкин А.В. Сборник задач по физике, 7-9 кл.: 5-е изд., стереотип. — М: Издательство «Экзамен», 2010.
- Интернет-портал Physics.ru ().
- Интернет-портал Festival.1september.ru ().
- Интернет-портал Fizportal.ru ().
- Интернет-портал Elkin52.narod.ru ().
Домашнее задание
- В каких случаях работа равна нулю?
- Как находится работа на пути, пройденном в направлении действия силы? В противоположном направлении?
- Какую работу совершает сила трения, действующая на кирпич, при его перемещении на 0,4 м? Сила трения равна 5 Н.
В повседневной жизни часто приходится встречаться с таким понятием как работа. Что это слово означает в физике и как определить работу силы упругости? Ответы на эти вопросы вы узнаете в статье.
Механическая работа
Работа — это скалярная алгебраическая величина, которая характеризует связь между силой и перемещением. При совпадении направления этих двух переменных она вычисляется по следующей формуле:
- F — модуль вектора силы, которая совершает работу;
- S — модуль вектора перемещения.
Не всегда сила, которая действует на тело, совершает работу. Например, работа силы тяжести равна нулю, если ее направление перпендикулярно перемещению тела.
Если вектор силы образует отличный от нуля угол с вектором перемещения, то для определения работы следует воспользоваться другой формулой:
A=FScosα
α — угол между векторами силы и перемещения.
Значит, механическая работа — это произведение проекции силы на направление перемещения и модуля перемещения, или произведение проекции перемещения на направление силы и модуля этой силы.
Знак механической работы
В зависимости от направления силы относительно перемещения тела работа A может быть:
- положительной(0°≤ α
- отрицательной(90°
- равной нулю(α=90°).
Если A>0, то скорость тела увеличивается. Пример — падение яблока с дерева на землю. При A
Единица измерения работы в СИ (Международной системе единиц) — Джоуль (1Н*1м=Дж). Джоуль — это работа силы, значение которой равно 1 Ньютону, при перемещении тела на 1 метр в направлении действия силы.
Работа силы упругости
Работу силы можно определить и графическим способом. Для этого вычисляется площадь криволинейной фигуры под графиком F s (x).
Так, по графику зависимости силы упругости от удлинения пружины, можно вывести формулу работы силы упругости.
Она равна:
A=kx 2 /2
- k — жесткость;
- x — абсолютное удлинение.
Что мы узнали?
Механическая работа совершается при действии на тело силы, которая приводит к перемещению тела. В зависимости от угла, который возникает между силой и перемещением, работа может быть равна нулю или иметь отрицательный или положительный знак. На примере силы упругости вы узнали о графическом способе определения работы.
Энергетические характеристики движения вводятся на основе понятия механической работы или работы силы.
Определение 1
Работа А, совершаемая постоянной силой F → , — это физическая величина, равная произведению модулей силы и перемещения, умноженному на косинус угла α, располагаемого между векторами силы F → и перемещением s → .
Данное определение рассматривается на рисунке 1 . 18 . 1 .
Формула работы записывается как,
A = F s cos α .
Работа – это скалярная величина. Это дает возможность быть положительной при (0 ° ≤ α
Джоуль равняется работе, совершаемой силой в 1 Н на перемещение 1 м по направлению действия силы.
Рисунок 1 . 18 . 1 . Работа силы F → : A = F s cos α = F s s
При проекции F s → силы F → на направление перемещения s → сила не остается постоянной, а вычисление работы для малых перемещений Δ s i суммируется и производится по формуле:
A = ∑ ∆ A i = ∑ F s i ∆ s i .
Данная сумма работы вычисляется из предела (Δ s i → 0) , после чего переходит в интеграл.
Графическое изображение работы определяют из площади криволинейной фигуры, располагаемой под графиком F s (x) рисунка 1 . 18 . 2 .
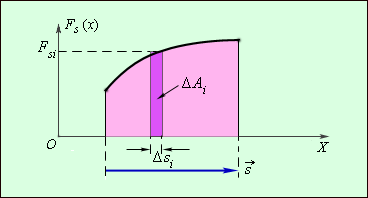
Рисунок 1 . 18 . 2 . Графическое определение работы Δ A i = F s i Δ s i .
Примером силы, зависящей от координаты, считается сила упругости пружины, которая подчиняется закону Гука. Чтобы произвести растяжение пружины, необходимо приложить силу F → , модуль которой пропорционален удлинению пружины. Это видно на рисунке 1 . 18 . 3 .
Рисунок 1 . 18 . 3 . Растянутая пружина. Направление внешней силы F → совпадает с направлением перемещения s → . F s = k x , где k обозначает жесткость пружины.
F → у п р = — F →
Зависимость модуля внешней силы от координат x можно изобразить на графике с помощью прямой линии.
Рисунок 1 . 18 . 4 . Зависимость модуля внешней силы от координаты при растяжении пружины.
Из выше указанного рисунка возможно нахождение работы над внешней силой правого свободного конца пружины, задействовав площадь треугольника. Формула примет вид
Данная формула применима для выражения работы, совершаемой внешней силой при сжатии пружины. Оба случая показывают, что сила упругости F → у п р равняется работе внешней силы F → , но с противоположным знаком.
Определение 2
Если на тело действует несколько сил, то формула общей работы будет выглядеть, как сумма всех работ, совершаемых над ним. Когда тело движется поступательно, точки приложения сил перемещаются одинаково, то есть общая работа всех сил будет равна работе равнодействующей приложенных сил.
Рисунок 1 . 18 . 5 . Модель механической работы.
Определение мощности
Определение 3
Мощностью называют работу силы, совершаемую в единицу времени.
Запись физической величины мощности, обозначаемой N , принимает вид отношения работы А к промежутку времени t совершаемой работы, то есть:
Определение 4
Система С И использует в качестве единицы мощности ватт (В т) , равняющийся мощности силы, которая совершает работу в 1 Д ж за время 1 с.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter