Обратите внимание, что у работы и энергии одинаковые единицы измерения. Это означает, что работа может переходить в энергию. Например, для того, чтобы тело поднять на некоторую высоту, тогда оно будет обладать потенциальной энергией , необходима сила, которая совершит эту работу. Работа силы по поднятию перейдет в потенциальную энергию.
Правило определения работы по графику зависимости F(r): работа численно равна площади фигуры под графиком зависимости силы от перемещения.

Угол между вектором силы и перемещением
1) Верно определяем направление силы, которая выполняет работу; 2) Изображаем вектор перемещения; 3) Переносим вектора в одну точку, получаем искомый угол.

На рисунке на тело действуют сила тяжести (mg), реакция опоры (N), сила трения (Fтр) и сила натяжения веревки F, под воздействием которой тело совершает перемещение r.
Работа силы тяжести

Работа реакции опоры

Работа силы трения

Работа силы натяжения веревки

![]()
Работа равнодействующей силы
Работу равнодействующей силы можно найти двумя способами: 1 способ — как сумму работ (с учетом знаков «+» или «-«) всех действующих на тело сил, в нашем примере 2 способ — в первую очередь найти равнодействующую силу, затем непосредственно ее работу, см. рисунок

![]()
Работа силы упругости
Для нахождения работы, совершенной силой упругости, необходимо учесть, что эта сила изменяется, так как зависит от удлинения пружины. Из закона Гука следует, что при увеличении абсолютного удлинения, сила увеличивается.
Для расчета работы силы упругости при переходе пружины (тела) из недеформированного состояния в деформированное используют формулу


Мощность
Скалярная величина, которая характеризует быстроту выполнения работы (можно провести аналогию с ускорением , которое характеризует быстроту изменения скорости). Определяется по формуле

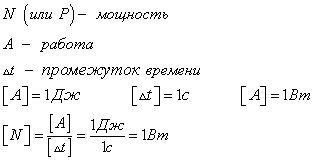
Коэффициент полезного действия
КПД — это отношение полезной работы, совершенной машиной, ко всей затраченной работе (подведенной энергии) за то же время


Коэффициент полезного действия выражается в процентах. Чем ближе это число к 100%, тем выше производительность машины. Не может быть КПД больше 100, так как невозможно выполнить больше работы, затратив меньше энергии.
КПД наклонной плоскости — это отношение работы силы тяжести, к затраченной работе по перемещению вдоль наклонной плоскости.
Главное запомнить
1) Формулы и единицы измерения; 2) Работу выполняет сила; 3) Уметь определять угол между векторами силы и перемещения
Если работа силы при перемещении тела по замкнутому пути равна нулю, то такие силы называют консервативными или потенциальными. Работа силы трения при перемещении тела по замкнутому пути никогда не равна нулю. Сила трения в отличие от силы тяжести или силы упругости является неконсервативной или непотенциальной.
Есть условия, при которых нельзя использовать формулу ![]() Если сила является переменной, если траектория движения является кривой линией. В этом случае путь разбивается на малые участки, для которых эти условия выполняются, и подсчитать элементарные работы на каждом из этих участков. Полная работа в этом случае равна алгебраической сумме элементарных работ:
Если сила является переменной, если траектория движения является кривой линией. В этом случае путь разбивается на малые участки, для которых эти условия выполняются, и подсчитать элементарные работы на каждом из этих участков. Полная работа в этом случае равна алгебраической сумме элементарных работ:
Значение работы некоторой силы зависит от выбора системы отсчета.
Содержание:
Электрический ток вырабатывается для того, чтобы в дальнейшем использовать его в определенных целях, для совершения какой-либо работы. Благодаря электричеству, функционируют все приборы, устройства и оборудование. Сама работа представляет собой определенные усилия, прилагаемые для перемещения электрического заряда на установленное расстояние. Условно, такая работа в пределах участка цепи, будет равна численному значению напряжения на данном участке.
Для выполнения необходимых расчетов необходимо знать, в чем измеряется работа тока. Все расчеты проводятся на основании исходных данных, полученных с помощью измерительных приборов. Чем больше величина заряда, тем больше усилий требуется для его перемещения, тем большая работа будет совершена.
Что называют работой тока
Электрический ток, как физическая величина, сам по себе не имеет практического значения. Наиболее важным фактором является действие тока, характеризующееся выполняемой им работой. Сама работа представляет собой определенные действия, в процессе которых один вид энергии превращается в другой. Например, электрическая энергия с помощью вращения вала двигателя, превращается в механическую энергию. Работа самого электрического тока заключается в движении зарядов в проводнике под действием электрического поля. Фактически вся работа по перемещению заряженных частиц выполняется электрическим полем.
С целью выполнения расчетов должна быть выведена формула работы электрического тока. Для составления формул понадобятся такие параметры, как сила тока и . Поскольку работа электрического тока и работа электрического поля — это одно и то же, она будет выражаться в виде произведения напряжения и заряда, протекающего в проводнике. То есть: A = Uq. Данная формула была выведена из соотношения, определяющего напряжение в проводнике: U = A/q. Отсюда следует, что напряжение представляет собой работу электрического поля А по переносу заряженной частицы q.
Сама заряженная частица или заряд отображается в виде произведения силы тока и времени, затраченного на движение этого заряда по проводнику: q = It. В этой формуле было использовано соотношение для силы тока в проводнике: I = q/t. То есть, является отношением заряда к промежутку времени, за которое заряд проходит через поперечное сечение проводника. В окончательном виде формула работы электрического тока будет выглядеть, как произведение известных величин: A = UIt.
В каких единицах измеряется работа электрического тока
Прежде чем непосредственно решать вопрос, в чем измеряется работа электрического тока, необходимо собрать единицы измерений всех физических величин, с помощью которых вычисляется этот параметр. Любая работа , следовательно, единицей измерения данной величины будет 1 Джоуль (1 Дж). Напряжение измеряется в вольтах, сила тока — в амперах, а время — в секундах. Значит единица измерения будет выглядеть следующим образом: 1 Дж = 1В х 1А х 1с.

Исходя из полученных единиц измерения, работа эл тока будет определяться, как произведение силы тока на участке цепи, напряжения на концах участка и промежутка времени, за которое ток протекает по проводнику.
Измерение проводятся с помощью , вольтметра и часов. Эти приборы позволяют эффективно решить проблему, как найти точное значение данного параметра. При включении амперметра и вольтметра в цепь, необходимо следить за их показаниями в течение установленного промежутка времени. Полученные данные вставляются в формулу, после чего выводится конечный результат.
Функции всех трех приборов объединяются в электросчетчиках, учитывающих потребленную энергию, а фактически работу, совершенную электротоком. Здесь используется уже другая единица — 1 кВт х ч, что также означает, сколько работы было совершено в течение единицы времени.
Чтобы иметь возможность охарактеризовать энергетические характеристики движения, было введено понятие механической работы. И именно ей в её разных проявлениях посвящена статья. Для понимания тема одновременно и лёгкая, и довольно сложная. Автор искренне старался сделать её более понятной и доступной для понимания, и остаётся только надеяться, что цель достигнута.
Что называют механической работой?
Что же так называют? Если над телом работает какая-то сила, и в результате действия оной тело перемещается, то это и называется механической работой. При подходе с точки зрения научной философии здесь можно выделить несколько дополнительных аспектов, но в статье будет тема раскрыта с точки зрения физики. Механическая работа — это не сложно, если хорошо вдуматься в написанные здесь слова. Но слово «механическая» обычно не пишется, и всё сокращается до слова «работа». Но не каждая работа является механической. Вот сидит человек и думает. Работает ли он? Мысленно да! Но механическая ли это работа? Нет. А если человек идёт? Если тело перемещается под действием силы, то это механическая работа. Всё просто. Иными словами, сила, действующая на тело, совершает (механическую) работу. И ещё: именно работой можно охарактеризовать результат действия определённой силы. Так ечли человек идёт, то определённые силы (трения, тяжести и т.д.) совершают над человеком механическую работу, и в результате их действия человек меняет точку своего нахождения, другими словами перемещается.
Работа как физическая величина равняется силе, что действует на тело, множимой на путь, который совершило тело под влиянием этой силы и в направлении, указываемом ею. Можно сказать, что механическая работа была сделана, если одновременно было соблюдено 2 условия: сила действовала на тело, и оно переместилось в направление её действия. Но она не совершалась или не совершается, если сила действовала, а тело не поменяло свое местонахождение в системе координат. Вот небольшие примеры, когда механическая работа не совершается:
- Так человек может навалиться на огромный валун с целью сдвинуть его, но сил не хватает. Сила действует на камень, а он не перемещается, и работа не происходит.
- Тело движется в системе координат, а сила равняется нулю или они все компенсировались. Такое можно наблюдать во время движения по инерции.
- Когда направление, в котором двигается тело, перпендикулярно действию силы. Когда поезд двигается по горизонтальной линии, то сила тяжести свою работу не совершает.

Зависимо от определённых условий механическая работа бывает отрицательной и положительной. Так, если направления и силы, и движения тела одинаковы, то происходит положительная работа. Примером положительной работы является действие силы тяжести на падающую каплю воды. Но если сила и направление движения противоположны, то значит происходит отрицательная механическая работа. Примером уже такого варианта является поднимающийся вверх воздушный шарик и сила тяжести, которая совершает отрицательную работу. Когда тело поддаётся влиянию нескольких сил, такая работа называется «работой результирующей силы».
Особенности практического применения (кинетическая энергия)

Переходим от теории к практической части. Отдельно следует поговорить о механической работе и её использовании в физике. Как многие наверняка вспомнили, вся энергия тела делится на кинетическую и потенциальную. Когда объект находится в положении равновесия и никуда не движется, его потенциальная энергия равняется общей энергии, а кинетическая равняется нулю. Когда начинается движение, потенциальная энергия начинает уменьшаться, кинетическая расти, но в сумме они равняются общей энергии объекта. Для материальной точки кинетическую энергию определяют как работу силы, которая ускорила точку от нуля до значения Н, а в формульном виде кинетика тела равна ½*М*Н, где М — масса. Чтобы узнать кинетическую энергию объекта, который состоит из множества частиц, необходимо найти сумму всей кинетической энергии частиц, и это будет кинетическая энергия тела.
Особенности практического применения (потенциальная энергия)
В случае, когда все действующие на тело силы консервативны, и потенциальная энергия равняется общей, то работа не совершается. Этот постулат известен как закон сохранения механической энергии. Механическая энергия в замкнутой системе является постоянной во временном интервале. Закон сохранения широко используют для решения задач из классической механики.
Особенности практического применения (термодинамика)

В термодинамике работа, которую совершает газ при расширении, рассчитывают по интегралу умножения давления на объем. Такой подход применим не только в тех случаях, когда есть точная функция объема, но и ко всем процессам, что могут быть отображены в плоскости давление/объем. Также применяется знание о механической работе не только к газам, но и ко всему, что может оказать давление.
Особенности практического применения на практике (теоретическая механика)

В теоретической механике все вышеописанные свойства и формулы рассматриваются более детально, в частности это проекции. Она даёт и свое определение для различных формул механической работы (пример определения для интеграла Риммера): предел, до которого стремится сумма всех сил элементарных работ, когда мелкость разбиения стремится к нулевому значению, называется работой силы вдоль кривой. Наверное, сложно? Но ничего, с теоретической механикой всё. Да уже и вся механическая работа, физика и другие сложности закончились. Дальше будут только примеры и заключение.
Единицы измерения механической работы
Для измерения работы в СИ используются джоули, а СГС использует эрг:
- 1 Дж = 1 кг·м²/с² = 1 Н·м
- 1 эрг = 1 г·см²/с² = 1 дин·см
- 1 эрг = 10 −7 Дж
Примеры механической работы
Для того чтобы разобраться окончательно с таким понятием как механическая работа, следует изучить несколько отдельных примеров, которые позволят рассмотреть её с множества, но далеко не всех сторон:
- Когда человек поднимает руками камень, то происходит механическая работа с помощью мускульной силы рук;
- Когда по рельсам едет поезд, его тянет сила тяги тягача (электровоза, тепловоза и т.д.);
- Если взять ружье и выстрелить из него, то благодаря силе давления, которую создадут пороховые газы, будет сделана работа: пуля перемещена вдоль ствола ружья одновременно с увеличением скорости самой пули;
- Механическая работа есть и тогда, когда сила трения действует на тело, заставляя его уменьшить скорость своего движения;
- Вышеописанный пример с шарами, когда они поднимаются в противоположную сторону относительно направления силы тяжести, тоже является примером механической работы, но кроме силы тяжести действует ещё и сила Архимеда, когда вверх поднимается всё, что легче воздуха.
Что такое мощность?

Напоследок хочется затронуть тему мощности. Работу силы, которая совершается в одну единицу времени, и называют мощностью. По сути мощность — это такая физическая величина, которая является отображением отношения работы к определённому промежутку времени, во время которого эта работа и совершалась: М=Р/В, где М — мощность, Р — работа, В — время. Единицу мощности в СИ обозначают в 1 Вт. Ватт равняется мощности, которая совершает работу в один джоуль за одну секунду: 1 Вт=1Дж1с.
Энергетические характеристики движения вводятся на основе понятия механической работы или работы силы.
Определение 1
Работа А, совершаемая постоянной силой F → , — это физическая величина, равная произведению модулей силы и перемещения, умноженному на косинус угла α, располагаемого между векторами силы F → и перемещением s → .
Данное определение рассматривается на рисунке 1 . 18 . 1 .
Формула работы записывается как,
A = F s cos α .
Работа – это скалярная величина. Это дает возможность быть положительной при (0 ° ≤ α
Джоуль равняется работе, совершаемой силой в 1 Н на перемещение 1 м по направлению действия силы.
Рисунок 1 . 18 . 1 . Работа силы F → : A = F s cos α = F s s
При проекции F s → силы F → на направление перемещения s → сила не остается постоянной, а вычисление работы для малых перемещений Δ s i суммируется и производится по формуле:
A = ∑ ∆ A i = ∑ F s i ∆ s i .
Данная сумма работы вычисляется из предела (Δ s i → 0) , после чего переходит в интеграл.
Графическое изображение работы определяют из площади криволинейной фигуры, располагаемой под графиком F s (x) рисунка 1 . 18 . 2 .

Рисунок 1 . 18 . 2 . Графическое определение работы Δ A i = F s i Δ s i .
Примером силы, зависящей от координаты, считается сила упругости пружины, которая подчиняется закону Гука. Чтобы произвести растяжение пружины, необходимо приложить силу F → , модуль которой пропорционален удлинению пружины. Это видно на рисунке 1 . 18 . 3 .

Рисунок 1 . 18 . 3 . Растянутая пружина. Направление внешней силы F → совпадает с направлением перемещения s → . F s = k x , где k обозначает жесткость пружины.
F → у п р = — F →
Зависимость модуля внешней силы от координат x можно изобразить на графике с помощью прямой линии.

Рисунок 1 . 18 . 4 . Зависимость модуля внешней силы от координаты при растяжении пружины.
Из выше указанного рисунка возможно нахождение работы над внешней силой правого свободного конца пружины, задействовав площадь треугольника. Формула примет вид
Данная формула применима для выражения работы, совершаемой внешней силой при сжатии пружины. Оба случая показывают, что сила упругости F → у п р равняется работе внешней силы F → , но с противоположным знаком.
Определение 2
Если на тело действует несколько сил, то формула общей работы будет выглядеть, как сумма всех работ, совершаемых над ним. Когда тело движется поступательно, точки приложения сил перемещаются одинаково, то есть общая работа всех сил будет равна работе равнодействующей приложенных сил.

Рисунок 1 . 18 . 5 . Модель механической работы.
Определение мощности
Определение 3
Мощностью называют работу силы, совершаемую в единицу времени.
Запись физической величины мощности, обозначаемой N , принимает вид отношения работы А к промежутку времени t совершаемой работы, то есть:
Определение 4
Система С И использует в качестве единицы мощности ватт (В т) , равняющийся мощности силы, которая совершает работу в 1 Д ж за время 1 с.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
