Энтропия. Свойства энтропии. Закон возрастания энтропии в замкнутых системах. Закон неубывания энтропии

Понятие «энтропия» ввел немецкий физик Рудольф Юлиус Эмануэль Клаузиус для обозначения тенденции вещей к и изнашиванию. В 1865 году он писал:

«Я предлагаю назвать величину S [энергию, которой не хватает для работы] энтропией тела, от греческого слова превращение... Энергия Вселенной постоянна - энтропия Вселенной стремится к максимуму «.

Люди стареют. Дома рушатся. Звезды сгорают. Утесы оседают в море.

Закон энтропии - это перефразировка первых двух законов термодинамики, сформулированных за несколько лет до 1850 года в процессе поиска способов усовершенствования паровых двигателей. Французский физик Никола Леонар Сади Карно обнаружил, что процесс потери тепла можно направить на выполнение какой-либо работы. Англичанин Джеймс Пре-скотт Джоуль открыл явление конверсии: при каком-либо действии выделяется дополнительное тепло.

Первое начало термодинамики, которое сформулировали независимо друг от друга Джоуль и немецкий естествоиспытатель Юлиус Роберт Майер, утверждает, что энергию нельзя ни создать, ни уничтожить - она может только менять свою форму. Затем в 1850 году Клаузиус, основываясь на работах Карно, дал определение второго начала термодинамики: любая химическая система, будь то твердое тело, жидкость или газ, стремится к максимальному беспорядку. Поток энергии движется только в одном направлении, к термическому равновесию. Тепло передается от одного тела другому, и этот переход необратим. Тепло можно использовать только один раз - оно перетекает в более холодное тело, и извлечь его оттуда невозможно (не добавляя еще больше энергии). Великий шотландский ученый Джеймс Клерк Максвелл (1831–1879) заметил по этому поводу:

«Если вы бросите в море бокал, полный воды, вы не сможете достать из воды тот же самый бокал».

У закона энтропии есть параллели с двумя биологическими концепциями, рассмотренными нами в части первой: эффектом черной королевы и эволюционной гонкой вооружений. Мир изменяется, и чтобы сохранить то, что у нас было раньше, мы должны сделать больше, чем сделали вчера. Вещи можно содержать в порядке или даже улучшить (краска на доме может выцвести, но дом можно покрасить снова еще лучше, чем раньше), но эта задача требует новых действий. Энергия системы разряжается и теряется, поэтому жизнь требует вливаний новой энергии.

Поддержание успеха требует постоянных усилий. Естественное состояние природы не равновесие, а энтропия. Конкурентное положение компании основывается на сложных взаимосвязях уникальных ресурсов и отношений, живых и беспокойных. Так же как любые системы и любые отношения, эти взаимосвязи, если о них не заботиться, не подкреплять и не обновлять, слабеют и распадаются. Противостоять энтропии вполне возможно (иначе как бы мы смогли накопить столько материальных ценностей за последние 250 лет?), но эта задача требует постоянных инноваций и улучшенного использования имеющейся в наличии энергии.

Возьмем какой-либо обратимый цикл (рис.8.13) и выделим в нем

Для рассматриваемого цикла

Если изменить направление перехода, то в силу обратимости процесса, каждое слагаемое суммы должно изменить знак. Так, если при направлении процесса от состояния (1) к состоянию (2) система получает от какого-то тела с температурой Т количество тепла Q, то при направлении процесса (2-1) на том же участке система должна отдавать этому же телу с температурой Т такое же количество Q, т.е. получить -Q.

Таким образом,

Исходя из неравенств (8.15) и (8.16), можно получить следующее соотношение:

Отсюда следует, что

т.е. сумма приведенных количеств тепла, полученных системой при обратимом переходе от одного состояния (начальное) в другое (конечное), не зависит от пути, по которому совершается переход и, следовательно, зависит только от начального и конечного состояний. Величины, изменения которых при переходе из одного состояния в другие не зависят от пути перехода, называются функциями состояния. Независимость суммы от пути, по которому совершается обратимый переход из состояния (1) в состояние (2) дает основание утверждать, что при обратимом процессе представляет собой приращение некоторой функции состояния. Эта функция была названа энтропией и обозначается буквой S.

Таким образом,

Согласно этому равенству, приращение энтропии равно элементарному количеству тепла, получаемому обратимо системой извне, отнесенному к температуре, при которой это тепло получается. Поскольку энтропия - функция состояния, сумма приращений энтропии должна быть равна разности значений энтропии в конечном и начальном состояниях:

Более того, суммы должны быть заменены интегралом

Итак, при обратимом процессе сумма приведенных количеств тепла равна приращению энтропии.

Выясним, в каком соотношении находятся сумма приведенных количеств тепла и приращение энтропии при необратимом процессе. Для этого рассмотрим цикл, состоящий из обратимой и необратимой ветвей

Разобьем эту сумму на две части, отнесенные к разным ветвям:

Вторая из этих сумм равна разности энтропий в состояниях 1 и 2 (8.17). Поэтому соотношение (8.18) можно записать в виде

Т.е. приращение энтропии больше или равна сумме приведенных количеств тепла.

Знак равенства соответствует любому обратимому переходу 12. Знак неравенства - любому необратимому переходу из состояния (1) в состояние (2). Температура Т означает температуру того тела, от которого система получает тепло Q.

При обратимом процессе эта температура совпадает с температурой системы. Если система изолирована, т.е. не обменивается теплом, то все Q будут равны нулю, вследствие чего

или, соответственно,

Таким образом, энтропия изолированной системы может только возрастать (если в системе протекает необратимый процесс), либо оставаться постоянной (если в системе протекает обратимый процесс). Убывать энтропия изолированной системы не может.

Если система обменивается теплом с внешней средой, ее энтропия может вести себя любым образом. В частности, если система отдает тепло внешним телам, энтропия системы уменьшается. Если неизолированная система совершает цикл, то ее энтропия возрастая на одних участках цикла и убывая на других, в конце цикла принимает первоначальное значение.

Энтропия - аддитивная величина. Это означает, что энтропия системы равна сумме энтропий отдельных ее частей.

Второй закон термодинамики. Энтропия.

Второй закон связан с понятием энтропии, являющейся мерой хаоса (или мерой порядка). Второй закон термодинамики гласит, что для вселенной в целом энтропия возрастает.

Существует два классических определения второго закона термодинамики:

• Кельвина и Планка

Не существует циклического процесса, который извлекает количество теплоты из резервуара при определенной температуре и полностью превращает эту теплоту в работу. (Невозможно построить периодически действующую машину, которая не производит ничего другого, кроме поднятия груза и охлаждения резервуара теплоты)

• Клаузиуса

Не существует процесса, единственным результатом которого является передача количества теплоты от менее нагретого тела к более нагретому. (Невозможен круговой процесс, единственным результатом которого было бы производство работы за счет охлаждения теплового резервуара)

Оба определения второго закона термодинамики опираются на первый закон термодинамики, утверждающий, что энергия убывает.

Второй закон связан с понятием энтропии (S) .

Энтропия порождается всеми процессами, она связана с потерей системы способности совершать работу. Рост энтропии - стихийный процесс. Если объем и энергия системы постоянны, то любое измение в системе увеличивает энтропию. Если же объем или энергия системы меняются, энтропия системы уменьшается. Однако, энтропия вселенной при этом не уменьшается.

Для того, чтобы энергию можно было использовать, в системе должны быть области с высоким и низким уровнями энергии. Полезная работа производится в результате передачи энергии от области с высоким уровнем энергии к области с низким уровнем энергии.

• 100% энергии не может быть преобразовано в работу
• Энтропия может вырабатываться, но не может быть уничтожена

Эффективность теплового двигателя

Эффективность теплового двигателя, действующего между двумя энергетическими уровнями, определена в пересчете на абсолютные температуры

η = (T h - T c) / T h = 1 - T c / T h

η = эффективность

T c = нижняя граница температуры (K)

Для того, чтобы достичь максимальной эффективности T c должна быть на столько низкой, на сколько это возможно. Чтобы эффект был 100% -м, T c должна равнятся 0 по шкале Kельвина. Практически это невозможно, поэтому эффективность всегда меньше 1 (менее 100%).

• Изменение энтропии > 0
  Необратимый процесс
• Изменение энтропии= 0
  Двусторонний процесс (обратимый)
• Изменение энтропии < 0
  Невозможный процесс (неосуществимый)

Энтропия определяет относительную способность одной системы влиять на другую. Когда энергия двигается к нижнему энергетическому уровню, где уменьшается возможность влияния на окружающую среду, энтропия увеличивается.

Определение энтропии

Энтропия определяется как:

T = абсолютная температура (K)

Изменение энтропии системы вызвано изменением содержания темпла в ней. Изменение энтропии равно изменению темпла системы деленной на среднюю абсолютную температуру (T a):

Сумма значений (H / T) для каждого полного цикла Карно равна 0. Это происходит из-за того, что каждому положительному H противостоит отрицательное значение H.

• Тепловой цикл Карно

Цикл Карно— идеальный термодинамический цикл.

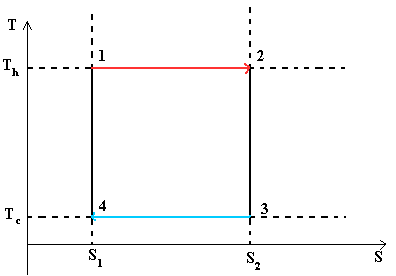
В тепловом двигателе, газ (реверсивно) нагревается (reversibly heated), а затем охлаждается. Модель цика следующая: Положение 1 --() --> Положение 2 --() --> Положение 3 --(изотермическое сжатие) --> Положение 4 --(адиабатическое сжатие) --> Положение 1

Положение 1 - Положение 2: Изотермическое расширение
Изотермическое расширение. В начале процесса рабочее тело имеет температуру T h , то есть температуру нагревателя. Затем тело приводится в контакт с нагревателем, который изотермически (при постоянной температуре) передаёт ему количество теплоты Q H . При этом объём рабочего тела увеличивается. Q H =∫Tds=T h (S 2 -S 1) =T h ΔS
Положение 2 - Положение 3: Адиабатическое расширение
Адиабатическое (изоэнтропическое) расширение. Рабочее тело отсоединяется от нагревателя и продолжает расширяться без теплообмена с окружающей средой. При этом его температура уменьшается до температуры холодильника.
Положение 3 - Положение 4: Изотермическое сжатие
Изотермическое сжатие. Рабочее тело, имеющее к тому времени температуру T c , приводится в контакт с холодильником и начинает изотермически сжиматься, отдавая холодильнику количество теплоты Q c . Q c =T c (S 2 -S 1)=T c ΔS
Положение 4 - Положение 1: Адиабатическое сжатие
Адиабатическое (изоэнтропическое) сжатие. Рабочее тело отсоединяется от холодильника и сжимается без теплообмена с окружающей средой. При этом его температура увеличивается до температуры нагревателя.

При изотермических процессах температура остаётся постоянной, при адиабатических отсутствует теплообмен, а значит, сохраняется энтропия.

Поэтому цикл Карно удобно представить в координатах T и S (температура и энтропия).

Законы термодинамики были определены эмперическим путем (эксперементально). Второй закон термодинамики - это обощение экспериментов, связанных с энтропией. Известно, что dS системы плюс dS окружающей среды равно или больше 0.

• Энтропия адиабатически изолированной системы не меняется!

Пример - Энтропия при нагревании воды

Процесс нагревания 1 кг воды от 0 до 100 o C (273 до 373 K)

При 0 o C = 0 кДж/кг (удельная - на единицу массы)

При 100 o C = 419 кДж/кг

Изменение удельной энтропии:

dS = dH / T a

= ((419 кДж/кг) - (0 кДж/кг)) / ((273 К + 373 К)/2)

= 1.297 кДж/кг*К

Пример - Энтропия при испарении воды

Процесс превращения 1 кг воды при 100 o C (373 K) в насыщенный пар при 100 o C (373 K) при нормальных условиях.

Удельная энтальпия пара при 100 o C (373 K) до испарения = 0 кДж/кг

100 o C (373 K) при испарении = 2 258 кДж/кг

Изменение удельной энтропии:

dS = dH / T a

= (2 258 - 0) / ((373 + 373)/2)

= 6.054 кДж/кг*К

Полное изменение удельной энтропии испарения воды - это сумма удельной энтропии воды (при 0 o C) плюс удельная энтропия пара (при температуре 100 o C).

Закон возрастания энтропии как одна из формулировок второго начала термодинамики

Рассмотрим замкнутую систему, которая переходит из состояния 1 в состояние 2 (рис.1) по пути $L_1$. Из состояния 2 в состояние 1 вернем систему с помощью обратимого процесса по пути $L_2$, но при этом мы понимаем, что система уже не является изолированной.

Так, мы получили цикл, к которому применимо неравенство Клаузиуса:

При переходе по пути $L_1$ система была изолированной, следовательно:

Переход 2-1 обратимый, следовательно, можно считать, что в этом процессе:

Иначе неравенство (4) запишем как:

Неравенство (5) означает, что при переходе замкнутой системы из состояния 1 в состояние 2 энтропия либо увеличивается, либо не изменяется. Закон возрастания энтропии (5) также относят к одной из формулировок второго начала термодинамики.

Возрастание и убывание энтропии

В процессах, которые протекают в изолированных системах, энтропия не убывает. В этом утверждении существенно то, что система должна быть изолирована. В неизолированных системах энтропия может и возрастать, и убывать и не изменяться. Энтропия не изменяется только в обратимых процессах. В необратимых процессах энтропия возрастает. Так как на практике процессы в системе, которая предоставлена самой себе, обычно необратимы, это значит, что энтропия изолированной системы обычно растет. Рост энтропии в изолированной системе означает, что система стремится к равновесному состоянию, которое является наиболее вероятным. Закон убывания энтропии в изолированной системе не запрещает полностью рост энтропии. Возможны отклонения, когда на каком-то отрезке времени система движется в направлении наименее вероятных состояний, то есть энтропия убывает или не меняется. И чем меньше система, тем роль таких флуктуаций больше. Однако для макросистем закон не убывания энтропии абсолютен.

Пример 1

Задание: Пусть имеется теплоизолированный сосуд, разделенный на две части перегородкой. Объемы частей $V_1$ и $V_2.$ В первой части находится ${\nu }_1$ молей идеального газа, во второй ${\nu }_2$ молей идеального газа. Температура в обеих частях сосуда одинакова и равна T. Перегородку убирают. Вычислите, как изменится энтропия газа ($\triangle S$) после установления равновесия.

Так как система считается теплоизолированной, газы идеальные, то внутренняя энергия таких газов зависит только от температуры и при смешении газов не изменяется. Заменим имеющийся в условиях задачи неравновесный процесс, равновесным в котором, каждая часть газа, расширяясь, занимает объем $V_1+V_2$. В таком случае для сконструированного нами обратимого процесса можно записать:

\[\triangle S=\int\limits^{(2)}_{(1)}{dS}=\int\limits^{V_1+V_2}_{V_1}{\frac{pdV}{T}}+\int\limits^{V_1+V_2}_{V_2}{\frac{pdV}{T}\left(1.1\right),}\]

Используем уравнение Менделеева -- Клайперона для идеального газа, выразим $\frac{p}{T}$, имеем:

\[\ pV=\nu RT\to \frac{\ p}{T}=\nu \frac{R}{V}\ \left(1.2\right),\]

Подставим (1.2) в (1.1), получим:

\[\triangle S=\int\limits^{V_1+V_2}_{V_1}{\frac{pdV}{T}}+\int\limits^{V_1+V_2}_{V_2}{\frac{pdV}{T}={\nu }_1R\int\limits^{V_1+V_2}_{V_1}{\frac{dV}{V}}+{\nu }_2R\int\limits^{V_1+V_2}_{V_2}{\frac{dV}{V}}={\nu }_1Rln\frac{V_1+V_2}{V_1}+{\nu }_2Rln\frac{V_1+V_2}{V_2}\left(1.3\right).}\]

Пример 2

Задание: Процесс расширения одноатомного идеального газа в количестве $\nu $ молей происходит так, что давление растет прямо пропорционально объему. Найти приращение энтропии газа, если объем в процессе увеличивается в а -- раз.

Процесс происходит с идеальным газом, следовательно, можем считать его обратимым и записать:

\[\triangle S=\int\limits^{\left(2\right)}_{\left(1\right)}{\frac{\delta Q}{T}\ \left(2.1\right).}\]

Из первого начала термодинамики мы знаем, что:

\[\delta Q=dU+pdV=\frac{i}{2}\nu RdT+pdV\left(2.2\right).\]

Подставим (2.2) в (2.1), получим:

\[\triangle S=\frac{i}{2}\nu R\int\limits^{T_2}_{T_1}{\frac{dT}{T}+\int\limits^{\left(2\right)}_{\left(1\right)}{\frac{pdV}{T}\left(2.3\right).}}\]

Запишем уравнение Менделеева -- Клайперона для того, чтобы выразить $\frac{p}{T},$ имеем:

Подставим (2.4) в (2.3), получим:

\[\triangle S=\frac{i}{2}\nu Rln\frac{T_2}{T_1}+\nu R\int\limits^{V_2}_{V_1}{\frac{dV}{V}=\frac{i}{2}нRln\frac{T_2}{T_1}+нRln\frac{V_2}{V_1}\left(2.5\right).}\]

Отношение объемов нам известно из условий задачи: $\frac{V_2}{V_1}=a.$ Выразим отношение температур. Используем для этого уравнение Менделеева - Клайперона и заданное в условиях задачи уравнение процесса ($p=bV$), где $b=const$:

\ \

Разделим (2.7) на (2.6) и используем уравнение процесса:

\[\frac{T_2}{T_1}=\frac{p_2V_2}{p_1V_1}\to \frac{T_2}{T_1}=\frac{b{V_2}^2}{b{V_1}^2}={\left(\frac{V_2}{V_1}\right)}^2\left(2.8\right).\]

Подставим (2.8) в (2.5), получим искомое изменение энтропии:

\[\triangle S=\frac{i}{2}\nu Rln{\left(\frac{V_2}{V_1}\right)}^2+\nu Rln\frac{V_2}{V_1}=i\nu Rln\left(a\right)+\nu Rln\left(a\right)=\nu Rln\left(a\right)\left(i+1\right)\left(2.7\right).\]

Ответ: Изменение энтропии в заданном процессе $\triangle S=\nu Rln\left(a\right)\left(i+1\right)$.

Формулировка теоремы

Если в некоторый момент времени энтропия замкнутой системы отлична от максимальной, то в последующие моменты энтропия не убывает - увеличивается или в предельном случае остается постоянной.

Локальное убывание энтропии

Вероятность перехода в состояния с большей энтропией настолько подавляюще велика по сравнению с вероятностью сколько-нибудь заметного ее уменьшения, что последнее вообще фактически никогда не может наблюдаться в природе.

Обратимые и необратимые процессы

Так как во всех осуществляющихся в природе замкнутых системах энтропия никогда не убывает - она увеличивается или, в предельном случае, остается постоянной - все процессы, происходящие с макроскопическими телами, можно разделить на необратимые и обратимые .

Под первыми подразумеваются процессы, сопровождающиеся возрастанием энтропии всей замкнутой системы. Процессы, которые были бы их повторениями в обратном порядке - не могут происходить, так как при этом энтропия должна была бы уменьшиться.
Обратимыми же называют процессы, при которых термодинамическая энтропия замкнутой системы остается постоянной. (Энтропия отдельных частей системы при этом не обязательно будет постоянной.)

См. также

Литература

• Ландау, Л. Д. , Лифшиц, Е. М. Статистическая физика. Часть 1. - Издание 3-е, дополненное. - М .: Наука , 1976. - 584 с. - («Теоретическая физика» , том V).

Wikimedia Foundation . 2010 .

Смотреть что такое "Закон неубывания энтропии" в других словарях:

Начала термодинамики Статья является частью серии «Термодинамика». Нулевое начало термодинамики Первое начало термодинамики Второе начало термодинамики Третье начало термодинамики Разделы термодинамики … Википедия

Начала термодинамики Статья является частью серии … Википедия

Термодинамика … Википедия

Термодинамические величины … Википедия

Статистическая физика … Википедия

- (от др. греч. θερμη тепло и др. греч. δυναμις сила) раздел физики, изучающий соотношения и превращения теплоты и других форм энергии. В отдельные дисциплины выделились химическая термодинамика, изучающая физико химические… … Википедия

У этого термина существуют и другие значения, см. Золотой век (значения). Золотой век общей теории относительности период примерно с 1960 до 1975 года, в течение которого исследования в общей теории относительности, ранее считавшейся просто… … Википедия

- («симметрия по отношению к обращению времени») симметрия уравнений, описывающих законы физики, по отношению к операции замены времени t на −t (то есть к обращению времени). В квантовой механике математически записывается, как равенство нулю … Википедия

T симметрия(«симметрия по отношению к обращению времени») симметрия уравнений, описывающих законы физики, по отношению к операции замены времени t на −t (то есть к обращению времени). В квантовой механике математически записывается, как равенство … Википедия

Книги

• Закон сохранения информации и его проявления в культуре , Черносвитов П.Ю.. Настоящая монография представляет собой культурологическое исследование, основания которого автором углублены в естественно-научную сферу, в ту ее часть, где лежат фундаментальные понятия ее…