Funciones trigonométricas

Este artículo contiene tablas de senos, cosenos, tangentes y cotangentes. Primero proporcionaremos una tabla de valores básicos. funciones trigonométricas, es decir, una tabla de senos, cosenos, tangentes y cotangentes de ángulos 0, 30, 45, 60, 90, ..., 360 grados ( 0, π/6, π/4, π/3, π/2,…, 2π radián). Después de esto, daremos una tabla de senos y cosenos, así como una tabla de tangentes y cotangentes de V. M. Bradis, y mostraremos cómo usar estas tablas para encontrar los valores de funciones trigonométricas.

Navegación de páginas.

Tabla de senos, cosenos, tangentes y cotangentes para ángulos de 0, 30, 45, 60, 90,... grados

Bibliografía.

• Álgebra: Libro de texto para noveno grado. promedio escuela/yu. N. Makarychev, N. G. Mindyuk, K. I. Neshkov, S. B. Suvorova; Ed. S. A. Telyakovsky - M.: Educación, 1990. - 272 págs.: enfermo - ISBN 5-09-002727-7.
• Bashmakov M.I.Álgebra y los inicios del análisis: Libro de texto. para 10-11 grados. promedio escuela - 3ª edición. - M.: Educación, 1993. - 351 p.: enfermo. - ISBN 5-09-004617-4.
• Álgebra y el inicio del análisis: Proc. para 10-11 grados. educación general instituciones / A. N. Kolmogorov, A. M. Abramov, Yu P. Dudnitsyn y otros; Ed. A. N. Kolmogorov - 14ª ed. - M.: Educación, 2004. - 384 págs.: Ill.
• Gusev V. A., Mordkovich A. G. Matemáticas (un manual para quienes ingresan a las escuelas técnicas): Proc. asignación.- M.; Más alto escuela, 1984.-351 p., enfermo.
• Bradis V.M. Tablas de matemáticas de cuatro dígitos: Para educación general. libro de texto establecimientos. - 2ª ed. - M.: Avutarda, 1999.- 96 p.: enfermo. ISBN 5-7107-2667-2

Comenzaremos nuestro estudio de trigonometría con el triángulo rectángulo. Definamos qué son el seno y el coseno, así como la tangente y cotangente de un ángulo agudo. Estos son los conceptos básicos de la trigonometría.

Recordemos que ángulo recto es un ángulo igual a 90 grados. Es decir, medio ángulo girado.

Esquina filosa- menos de 90 grados.

Ángulo obtuso- mayor a 90 grados. En relación con tal ángulo, "obtuso" no es un insulto, sino un término matemático :-)

Dibujemos un triángulo rectángulo. Un ángulo recto generalmente se denota por . Tenga en cuenta que el lado opuesto a la esquina está indicado con la misma letra, solo que en tamaño pequeño. Por tanto, el lado opuesto al ángulo A se designa.

El ángulo se denota con la letra griega correspondiente.

Hipotenusa de un triángulo rectángulo es el lado opuesto al ángulo recto.

Piernas- lados opuestos a ángulos agudos.

El cateto opuesto al ángulo se llama opuesto(relativo al ángulo). El otro cateto, que se encuentra en uno de los lados del ángulo, se llama adyacente.

Seno El ángulo agudo en un triángulo rectángulo es la razón entre el cateto opuesto y la hipotenusa:

Cosenoángulo agudo en un triángulo rectángulo: la relación entre el cateto adyacente y la hipotenusa:

Tangenteángulo agudo en un triángulo rectángulo: la relación entre el lado opuesto y el adyacente:

Otra definición (equivalente): la tangente de un ángulo agudo es la relación entre el seno del ángulo y su coseno:

Cotangenteángulo agudo en un triángulo rectángulo: la relación entre el lado adyacente y el opuesto (o, lo que es lo mismo, la relación entre el coseno y el seno):

Tenga en cuenta las relaciones básicas para seno, coseno, tangente y cotangente a continuación. Nos serán útiles a la hora de resolver problemas.

Probemos algunos de ellos.

Bien, hemos dado definiciones y escrito fórmulas. Pero ¿por qué todavía necesitamos seno, coseno, tangente y cotangente?

Lo sabemos la suma de los ángulos de cualquier triángulo es igual a.

Conocemos la relación entre fiestas triángulo rectángulo. Este es el teorema de Pitágoras: .

Resulta que conociendo dos ángulos de un triángulo, puedes encontrar el tercero. Conociendo los dos lados de un triángulo rectángulo, puedes encontrar el tercero. Esto significa que los ángulos tienen su propia proporción y los lados tienen la suya propia. Pero, ¿qué debes hacer si en un triángulo rectángulo conoces un ángulo (excepto el ángulo recto) y un lado, pero necesitas encontrar los otros lados?

Esto es lo que la gente del pasado encontraba al hacer mapas de la zona y del cielo estrellado. Después de todo, no siempre es posible medir directamente todos los lados de un triángulo.

Seno, coseno y tangente: también se les llama funciones de ángulos trigonométricos- dar relaciones entre fiestas Y esquinas triángulo. Conociendo el ángulo, puedes encontrar todas sus funciones trigonométricas utilizando tablas especiales. Y conociendo los senos, cosenos y tangentes de los ángulos de un triángulo y de uno de sus lados, podrás encontrar el resto.

También dibujaremos una tabla de los valores de seno, coseno, tangente y cotangente para los ángulos "buenos" desde hasta.

Tenga en cuenta los dos guiones rojos en la tabla. Para valores de ángulo apropiados, la tangente y la cotangente no existen.

Veamos varios problemas de trigonometría del banco de tareas FIPI.

1. En un triángulo, el ángulo es , . Encontrar .

El problema se resuelve en cuatro segundos.

Porque el , .

2. En un triángulo, el ángulo es , , . Encontrar .

Encontrémoslo usando el teorema de Pitágoras.

El problema esta resuelto.

A menudo, en los problemas hay triángulos con ángulos y o con ángulos y. ¡Recuerda de memoria las proporciones básicas para ellos!

Para un triángulo con ángulos y el cateto opuesto al ángulo en es igual a la mitad de la hipotenusa.

Un triángulo con ángulos y es isósceles. En él, la hipotenusa es veces más grande que el cateto.

Analizamos problemas para resolver triángulos rectángulos, es decir, encontrar lados o ángulos desconocidos. ¡Pero eso no es todo! EN Opciones del examen estatal unificado En matemáticas existen muchos problemas donde aparece el seno, coseno, tangente o cotangente del ángulo externo de un triángulo. Más sobre esto en el próximo artículo.

En el artículo entenderemos completamente cómo se ve. tabla de valores trigonométricos, seno, coseno, tangente y cotangente. Consideremos el significado básico de las funciones trigonométricas, desde un ángulo de 0,30,45,60,90,...,360 grados. Y veamos cómo utilizar estas tablas para calcular los valores de funciones trigonométricas.
Primero veamos tabla de coseno, seno, tangente y cotangente desde un ángulo de 0, 30, 45, 60, 90,... grados. La definición de estas cantidades nos permite determinar el valor de las funciones de ángulos de 0 y 90 grados:

sin 0 0 =0, cos 0 0 = 1. tg 00 = 0, la cotangente de 00 no estará definida
sin 90 0 = 1, cos 90 0 =0, ctg90 0 = 0, la tangente de 90 0 será incierta

Si tomamos triángulos rectángulos cuyos ángulos miden entre 30 y 90 grados. Obtenemos:

pecado 30 0 = 1/2, cos 30 0 = √3/2, tan 30 0 = √3/3, cos 30 0 = √3
pecado 45 0 = √2/2, cos 45 0 = √2/2, tan 45 0 = 1, cos 45 0 = 1
sen 60 0 = √3/2, cos 60 0 = 1/2, tg 60 0 =√3, cot 60 0 = √3/3

Representemos todos los valores obtenidos en la forma. tabla trigonométrica:

¡Tabla de senos, cosenos, tangentes y cotangentes!

Si utilizamos la fórmula de reducción, nuestra tabla aumentará, sumando valores para ángulos de hasta 360 grados. Se verá así:

Además, basándose en las propiedades de la periodicidad, la tabla se puede aumentar si reemplazamos los ángulos por 0 0 +360 0 *z .... 330 0 +360 0 *z, en el que z es un número entero. En esta tabla es posible calcular el valor de todos los ángulos correspondientes a puntos de un solo círculo.

Veamos cómo usar la tabla en una solución.
Todo es muy sencillo. Dado que el valor que necesitamos se encuentra en el punto de intersección de las celdas que necesitamos. Por ejemplo, toma el coseno de un ángulo de 60 grados, en la tabla se verá así:

En la tabla final de los principales valores de funciones trigonométricas se procede de la misma forma. Pero en esta tabla es posible averiguar cuánto es la tangente desde un ángulo de 1020 grados, = -√3 Comprobemos 1020 0 = 300 0 +360 0 *2. Encontrémoslo usando la tabla.

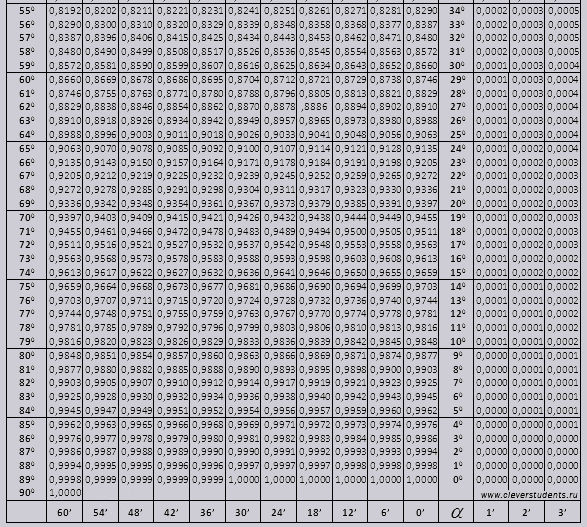
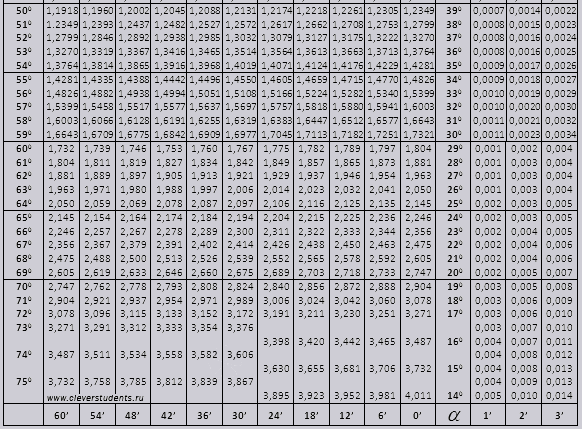
Mesa bradis. Para seno, coseno, tangente y cotangente.

Las tablas de Bradis se dividen en varias partes, que constan de tablas de coseno y seno, tangente y cotangente, que se dividen en dos partes (tg de ángulos de hasta 90 grados y ctg de ángulos pequeños).

Seno y coseno

tg de ángulo que comienza en 00 y termina en 760, ctg de ángulo que comienza en 140 y termina en 900.

tg hasta 900 y ctg de pequeños ángulos.

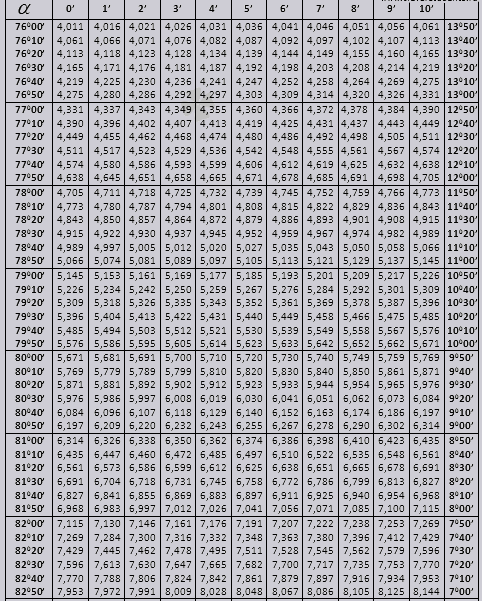
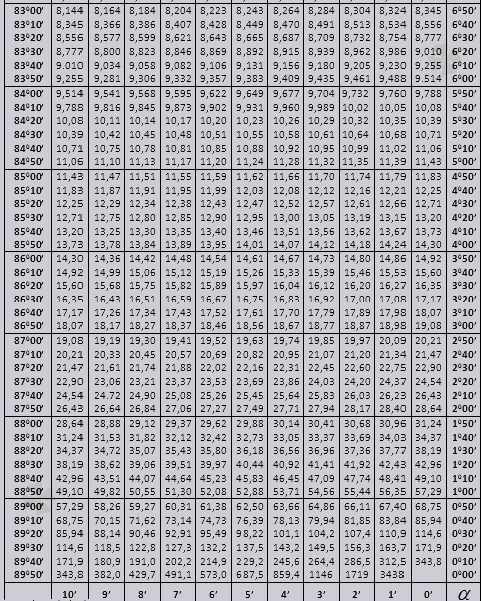
Averigüemos cómo utilizar las tablas Bradis para resolver problemas.

Busquemos la designación sin (la designación en la columna del borde izquierdo) 42 minutos (la designación está en la línea superior). Por intersección buscamos la designación, it = 0,3040.

Los valores de los minutos se indican con un intervalo de seis minutos, qué hacer si el valor que necesitamos cae exactamente dentro de este intervalo. Tomemos 44 minutos, pero solo hay 42 en la tabla. Tomamos 42 como base y usamos las columnas adicionales del lado derecho, tomamos la segunda enmienda y sumamos 0,3040 + 0,0006, obtenemos 0,3046.

Con sin 47 minutos, tomamos 48 minutos como base y le restamos 1 corrección, es decir, 0,3057 - 0,0003 = 0,3054

Al calcular cos, trabajamos de manera similar a sin, solo que tomamos como base la fila inferior de la tabla. Por ejemplo cos 20 0 = 0,9397

Los valores de ángulo tg hasta 90 0 y cot de ángulo pequeño son correctos y no existen correcciones en ellos. Por ejemplo, encuentre tg 78 0 37min = 4,967


y ctg 20 0 13min = 25,83

Bueno, hemos visto las tablas trigonométricas básicas. Esperamos que esta información te haya sido de gran utilidad. Si tienes alguna pregunta sobre las tablas, ¡asegúrate de escribirla en los comentarios!

Nota: Los topes de pared son tableros de parachoques para proteger las paredes. Siga el enlace parachoques de pared sin marco (http://www.spi-polymer.ru/otboyniki/) y obtenga más información.

Tabla de funciones trigonométricas básicas para ángulos de 0, 30, 45, 60, 90,... grados

A partir de las definiciones trigonométricas de las funciones $\sin$, $\cos$, $\tan$ y $\cot$, puedes encontrar sus valores para los ángulos $0$ y $90$ grados:

$\sin⁡0°=0$, $\cos0°=1$, $\tan 0°=0$, $\cot 0°$ no definido;

$\sin90°=1$, $\cos90°=0$, $\cot90°=0$, $\tan 90°$ no está determinado.

EN curso escolar En geometría, al estudiar triángulos rectángulos, encontramos funciones trigonométricas de los ángulos $0°$, $30°$, $45°$, $60°$ y $90°$.

Valores encontrados de funciones trigonométricas para los ángulos indicados en grados y radianes, respectivamente ($0$, $\frac(\pi)(6)$, $\frac(\pi)(4)$, $\frac(\ pi)(3) $, $\frac(\pi)(2)$) para facilitar la memorización y el uso se ingresan en una tabla llamada tabla trigonométrica, tabla de valores básicos de funciones trigonométricas etcétera.

Cuando se utilizan fórmulas de reducción, la tabla trigonométrica se puede expandir a un ángulo de $360°$ y, en consecuencia, $2\pi$ radianes:

Utilizando las propiedades de periodicidad de las funciones trigonométricas, cada ángulo, que diferirá del ya conocido en $360°$, se puede calcular y registrar en una tabla. Por ejemplo, la función trigonométrica para el ángulo $0°$ tendrá el mismo valor para el ángulo $0°+360°$, y para el ángulo $0°+2 \cdot 360°$, y para el ángulo $0°+3 \cdot 360°$ y etc.

Usando una tabla trigonométrica, puedes determinar los valores de todos los ángulos de un círculo unitario.

En un curso de geometría escolar, se supone que debes memorizar los valores básicos de las funciones trigonométricas recopiladas en una tabla trigonométrica para facilitar la resolución de problemas trigonométricos.

usando una mesa

En la tabla, basta con encontrar la función trigonométrica requerida y el valor del ángulo o radianes para el cual se debe calcular esta función. En la intersección de la fila con la función y la columna con el valor, obtenemos el valor deseado de la función trigonométrica del argumento dado.

En la figura puedes ver cómo encontrar el valor de $\cos⁡60°$, que es igual a $\frac(1)(2)$.

La tabla trigonométrica extendida se utiliza de la misma forma. La ventaja de utilizarlo es, como ya se mencionó, el cálculo de la función trigonométrica de casi cualquier ángulo. Por ejemplo, puedes encontrar fácilmente el valor $\tan 1 380°=\tan (1 380°-360°)=\tan(1 020°-360°)=\tan(660°-360°)=\tan300 °$:

Tablas Bradis de funciones trigonométricas básicas.

La capacidad de calcular la función trigonométrica de absolutamente cualquier valor de ángulo para un valor entero de grados y un valor entero de minutos se obtiene mediante el uso de tablas de Bradis. Por ejemplo, encuentre el valor de $\cos⁡34°7"$. Las tablas se dividen en 2 partes: una tabla de valores de $\sin$ y $\cos$ y una tabla de valores de $ \tan$ y $\cot$.

Las tablas Bradis permiten obtener valores aproximados de funciones trigonométricas con una precisión de hasta 4 decimales.

Usando tablas Bradis

Usando las tablas de Bradis para senos, encontramos $\sin⁡17°42"$. Para hacer esto, en la columna izquierda de la tabla de senos y cosenos encontramos el valor de grados - $17°$, y en la línea superior encontramos el valor de los minutos - $42"$. En su intersección obtenemos el valor deseado:

$\sin17°42"=0,304$.

Para encontrar el valor $\sin17°44"$ necesitas usar la corrección en el lado derecho de la tabla. En en este caso al valor $42"$, que está en la tabla, hay que agregarle una corrección de $2"$, que es igual a $0.0006$. Obtenemos:

$\sin17°44"=0,304+0,0006=0,3046$.

Para encontrar el valor $\sin17°47"$ también utilizamos la corrección del lado derecho de la tabla, solo que en este caso tomamos como base el valor $\sin17°48"$ y le restamos la corrección de $1"$ :

$\sin17°47"=0,3057-0,0003=0,3054$.

Al calcular cosenos, realizamos acciones similares, pero miramos los grados en la columna de la derecha y los minutos en la columna inferior de la tabla. Por ejemplo, $\cos20°=0,9397$.

No hay correcciones para valores de tangente de hasta $90°$ y cotangente de ángulo pequeño. Por ejemplo, encontremos $\tan 78°37"$, que según la tabla es igual a $4.967$.

1. Funciones trigonométricas son funciones elementales cuyo argumento es esquina. Usando funciones trigonométricas, las relaciones entre los lados y Esquinas filosas en un triángulo rectángulo. Los campos de aplicación de las funciones trigonométricas son extremadamente diversos. Por ejemplo, cualquier proceso periódico se puede representar como una suma de funciones trigonométricas (serie de Fourier). Estas funciones suelen aparecer al resolver ecuaciones diferenciales y funcionales.

2. Las funciones trigonométricas incluyen las siguientes 6 funciones: seno, coseno, tangente,cotangente, secante Y cosecante. Para cada una de estas funciones existe una función trigonométrica inversa.

3. Es conveniente introducir la definición geométrica de funciones trigonométricas utilizando circulo unitario. La siguiente figura muestra un círculo con radio r=1. El punto M(x,y) está marcado en el círculo. El ángulo entre el vector de radio OM y la dirección positiva del eje Ox es igual a α.

4. Seno El ángulo α es la relación entre la ordenada y del punto M(x,y) y el radio r:
senα=y/r.
Como r=1, entonces el seno es igual a la ordenada del punto M(x,y).

5. Coseno El ángulo α es la relación entre la abscisa x del punto M(x,y) y el radio r:
cosα=x/r

6. Tangente El ángulo α es la relación entre la ordenada y de un punto M(x,y) y su abscisa x:
tanα=y/x,x≠0

7. Cotangente El ángulo α es la relación entre la abscisa x de un punto M(x,y) y su ordenada y:
cotα=x/y,y≠0

8. Secante El ángulo α es la relación entre el radio r y la abscisa x del punto M(x,y):
segundoα=r/x=1/x,x≠0

9. Cosecante El ángulo α es la relación entre el radio r y la ordenada y del punto M(x,y):
cscα=r/y=1/y,y≠0

10. En el círculo unitario, las proyecciones x, y, los puntos M(x,y) y el radio r forman un triángulo rectángulo, en el que x,y son los catetos y r es la hipotenusa. Por lo tanto, las definiciones anteriores de funciones trigonométricas en el apéndice de triángulo rectángulo se formulan de la siguiente manera:
Seno El ángulo α es la razón entre el cateto opuesto y la hipotenusa.
Coseno El ángulo α es la relación entre el cateto adyacente y la hipotenusa.
Tangente Se llama ángulo α al cateto opuesto al adyacente.
Cotangente El ángulo α se llama lado adyacente al lado opuesto.
Secante El ángulo α es la relación entre la hipotenusa y el cateto adyacente.
Cosecante El ángulo α es la relación entre la hipotenusa y el cateto opuesto.

11. Gráfica de la función seno
y=sinx, dominio de definición: x∈R, rango de valores: −1≤sinx≤1

12. Gráfica de la función coseno
y=cosx, dominio: x∈R, rango: −1≤cosx≤1

13. Gráfica de la función tangente
y=tanx, rango de definición: x∈R,x≠(2k+1)π/2, rango de valores: −∞

14. Gráfica de la función cotangente
y=cotx, dominio: x∈R,x≠kπ, rango: −∞

15. Gráfica de la función secante
y=secx, dominio: x∈R,x≠(2k+1)π/2, rango: secx∈(−∞,−1]∪∪)