Rješavanje parcijalnih diferencijalnih jednadžbi mješovitog tipa. Diferencijalne jednadžbe za lutke. Primjeri rješenja

Neka X 1 , X 2 , ..., X n - navedene funkcije varijable x 1 , x 2 , ..., x n.

Rješavanje linearne homogene parcijalne diferencijalne jednadžbe prva narudžba:

potrebno je riješiti sustav običnih diferencijalnih jednadžbi (karakteristična jednadžba):
:
Zatim trebate predstaviti rješenje u obliku:
φ 1 (x 1 , x 2 , ..., x n ) = C 1,
φ 2 (x 1, x 2, ..., x n) = C 2,
..................
φ n- 1 (x 1 , x 2 , ..., x n ) = C n-1,
gdje su C k konstante.
Tada odmah dobivamo opće rješenje:
,
gdje je F proizvoljna funkcija od n - 1 argumenti.

Ako trebate dobiti određeno rješenje s određenim rubnim uvjetima, tada trebate zamijeniti vrijednosti varijabli iz rubnih uvjeta u opće rješenje i pronaći oblik funkcije F.

Linearne nehomogene parcijalne diferencijalne jednadžbe prvog reda

Neka X 1 , X 2 , ..., X n+1- zadane funkcije varijabli x 1 , x 2 , ..., x n i z.

Za rješavanje linearne nehomogene parcijalne diferencijalne jednadžbe prvog reda:
,
potrebno je riješiti jednadžbu karakteristika:
.
Rješenje ovog sustava treba prikazati u sljedećem obliku:
φ 1 (x 1 , x 2 , ..., x n , z ) = C 1,
φ 2 (x 1 , x 2 , ..., x n , z ) = C 2,
..................
φn (x 1 , x 2 , ..., x n , z ) = C n.
Nakon čega odmah dobivamo opći integral u implicitnom obliku:

gdje je F proizvoljna funkcija. Opći integral također se može prikazati u razne opcije, Na primjer:
φ 1 = F(φ 2, φ 3, ..., φ n),
φ 2 = F(φ 1, φ 3, ..., φ n),
itd.

Primjeri rješenja linearnih parcijalnih diferencijalnih jednadžbi prvog reda

Homogena jednadžba

Zadatak

Pronađite opće rješenje linearne homogene parcijalne diferencijalne jednadžbe prvog reda i riješite Cauchyjev problem sa zadanim rubnim uvjetom:
,
u .

Riješenje

Ovo je linearna homogena parcijalna diferencijalna jednadžba prvog reda. Napravimo jednadžbu karakteristika:

Ova jednadžba karakteristika sadrži tri jednadžbe:
;
;
.
Trebamo odabrati i riješiti bilo koja dva od njih. Tada će treći biti učinjen automatski.

Odaberemo i riješimo prvu jednadžbu:

Ovdje su varijable već odvojene, integrirajmo:

Tablični integrali,

Potencirajmo:

Odavde

Ili:

integrirajući faktor. Pomnožite s x -1 i pretvorite:



Integrirajmo:

Zamijenimo prethodno dobiveni izraz C 1 = x y 2:

Opće rješenje izvorne parcijalne diferencijalne jednadžbe je:

gdje je F proizvoljna funkcija dvaju argumenata F(φ 1, φ 2). Nađimo njegov oblik iz rubnog uvjeta
u .

Razmatramo rješenje na granici.
Stavimo x y = -1 :


Odavde


Na granici
.

F (φ 1, φ 2) = φ 1 φ 2.
Isti je izgled u cijeloj regiji.
Zamjena
;
,
dobivamo određeno rješenje izvorne parcijalne diferencijalne jednadžbe s danim rubnim uvjetom:

Odgovor

Uobičajena odluka:

gdje je F proizvoljna funkcija dvaju argumenata F (φ 1, φ 2).

Privatno rješenje:

Nehomogena jednadžba

Zadatak

Pronađite površinu koja zadovoljava ovu jednadžbu
,
i prolazi kroz zadanu kružnicu x + y + z = 0, x 2 + y 2 + z 2 = a 2.

Riješenje

Ovo je linearna nehomogena parcijalna diferencijalna jednadžba prvog reda. Napravimo jednadžbu karakteristika:

Sadrži tri jednadžbe:
;
;
.
Trebamo odabrati i riješiti bilo koja dva od njih. Tada će treći biti automatski zadovoljen. Odaberemo prvu i drugu jednadžbu.

Rješavamo jednadžbu:

Pomnožite s 2 z i integrirajte:

Tablični integrali,

Potencirajmo:

Odavde
x = C 1 g

Zamijenimo u drugu jednadžbu:


Ili:

To, dakle, primjećujemo

Ovo je linearna jednadžba. Rješavamo koristeći integrirajući faktor. Podijelite s y 2 i transformirajte:


Integrirajmo:

Zamijenimo ranije dobiveni izraz i transformirajmo:

Dakle, pronašli smo dva integrala jednadžbe karakteristika:

Radi lakšeg daljnjeg izračuna, imajte na umu da je funkcija konstante također konstantna. Stoga integrale zapisujemo u obliku:

Opći integral izvorne parcijalne diferencijalne jednadžbe ima oblik:
F (φ 1, φ 2) = 0
No, budući da je F proizvoljna funkcija dvaju argumenata, opći se integral također može napisati u obliku:
φ 1 = F(φ 2),
gdje je F proizvoljna funkcija jednog argumenta.

Nađimo oblik ove funkcije, razmatranje rješenja na granici.
Na granici je x 2 + y 2 + z 2 = a 2 , .
Iz jednadžbe x + y + z = 0, z = - (x+y). Zamijenite u x 2 + y 2 + z 2 = a 2 i transformirajte:
x2+y2+ (x + y) 2 = a 2
x 2 + y 2 + x 2 + 2 xy + y 2 = a 2
2 x 2 + 2 xy + 2 y 2 = a 2
Dijeleći s y 2, imamo

Dakle, pronašli smo da na granici:

.
Zamijenimo u izraz općeg integrala:
φ 1 = F(φ 2)
.
Napravimo zamjenu
:
.

Dakle, našli smo da na granici funkcija F ima oblik:
.
Isti je izgled dakle u cijeloj regiji
.
Zamijenimo izraze za φ 1 i φ 2:


.
Pomnožite s 2 y 2 .

Često samo spomen diferencijalne jednadžbečini da se učenici osjećaju nelagodno. Zašto se ovo događa? Najčešće, jer pri proučavanju osnova materijala nastaje praznina u znanju, zbog čega daljnje proučavanje difura postaje jednostavno mučenje. Nije jasno što učiniti, kako se odlučiti, odakle početi?

Ipak, pokušat ćemo vam pokazati da difurs nije tako težak kao što se čini.

Osnovni pojmovi teorije diferencijalnih jednadžbi

Iz škole znamo najjednostavnije jednadžbe u kojima treba pronaći nepoznati x. Zapravo diferencijalne jednadžbe samo malo drugačiji od njih – umjesto varijable x morate pronaći funkciju u njima y(x) , koji će jednadžbu pretvoriti u identitet.

D diferencijalne jednadžbe od velike su praktične važnosti. Ovo nije apstraktna matematika koja nema veze sa svijetom oko nas. Mnogi stvarni prirodni procesi opisani su pomoću diferencijalnih jednadžbi. Na primjer, titranje strune, gibanje harmonijskog oscilatora, pomoću diferencijalnih jednadžbi u problemima mehanike, pronaći brzinu i ubrzanje tijela. Također DU naširoko se koriste u biologiji, kemiji, ekonomiji i mnogim drugim znanostima.

Diferencijalna jednadžba (DU) je jednadžba koja sadrži derivacije funkcije y(x), samu funkciju, nezavisne varijable i druge parametre u raznim kombinacijama.

Postoje mnoge vrste diferencijalnih jednadžbi: obične diferencijalne jednadžbe, linearne i nelinearne, homogene i nehomogene, diferencijalne jednadžbe prvog i višeg reda, parcijalne diferencijalne jednadžbe i tako dalje.

Rješenje diferencijalne jednadžbe je funkcija koja je pretvara u identitet. Postoje opća i posebna rješenja za daljinski upravljač.

Opće rješenje diferencijalne jednadžbe je opći skup rješenja koja pretvaraju jednadžbu u identitet. Parcijalno rješenje diferencijalne jednadžbe je rješenje koje zadovoljava dodatne uvjete navedene na početku.

Red diferencijalne jednadžbe određen je najvišim redom njezinih izvodnica.

Obične diferencijalne jednadžbe

Obične diferencijalne jednadžbe su jednadžbe koje sadrže jednu nezavisnu varijablu.

Razmotrimo najjednostavniju običnu diferencijalnu jednadžbu prvog reda. Izgleda kao:

Takva se jednadžba može riješiti jednostavnim integriranjem njezine desne strane.

Primjeri takvih jednadžbi:

Odvojive jednadžbe

Općenito, ova vrsta jednadžbe izgleda ovako:

Evo primjera:

Prilikom rješavanja takve jednadžbe morate razdvojiti varijable, dovodeći ih u oblik:

Nakon toga preostaje integrirati oba dijela i dobiti rješenje.

Linearne diferencijalne jednadžbe prvog reda

Takve jednadžbe izgledaju ovako:

Ovdje su p(x) i q(x) neke funkcije nezavisne varijable, a y=y(x) je željena funkcija. Evo primjera takve jednadžbe:

Pri rješavanju takve jednadžbe najčešće se koriste metodom variranja proizvoljne konstante ili željenu funkciju prikazuju kao umnožak druge dvije funkcije y(x)=u(x)v(x).

Za rješavanje takvih jednadžbi potrebna je određena priprema i bit će ih prilično teško uzeti “na prvi pogled”.

Primjer rješavanja diferencijalne jednadžbe sa separabilnim varijablama

Dakle, pogledali smo najjednostavnije vrste daljinskog upravljanja. Sada pogledajmo rješenje jednog od njih. Neka ovo bude jednadžba sa separabilnim varijablama.

Prvo, prepišimo izvedenicu u poznatijem obliku:

Zatim podijelimo varijable, odnosno u jednom dijelu jednadžbe skupljamo sve "I", au drugom - "X":

Sada ostaje integrirati oba dijela:

Integriramo i dobivamo opće rješenje ove jednadžbe:

Naravno, rješavanje diferencijalnih jednadžbi svojevrsna je umjetnost. Morate biti u stanju razumjeti koja je to vrsta jednadžbe, i također naučiti vidjeti koje transformacije je potrebno napraviti s njom kako bi se došlo do jednog ili drugog oblika, da ne spominjemo samo sposobnost razlikovanja i integracije. A da biste uspjeli riješiti DE potrebna vam je praksa (kao i u svemu). A ako imate ovaj trenutak nemate vremena shvatiti kako se rješavaju diferencijalne jednadžbe, ili vam je Cauchyjev problem zapeo kao kost u grlu, ili ne znate, obratite se našim autorima. U kratkom vremenu pružit ćemo vam gotovo i detaljno rješenje čije detalje možete razumjeti u bilo kojem trenutku koji vam odgovara. U međuvremenu predlažemo da pogledate video na temu “Kako riješiti diferencijalne jednadžbe”:

Parcijalna diferencijalna jednadžba(posebni slučajevi su također poznati kao jednadžbe matematičke fizike, UMF) - diferencijalna jednadžba koja sadrži nepoznate funkcije više varijabli i njihove parcijalne derivacije.

Enciklopedijski YouTube

1 / 5

✪ Parcijalne diferencijalne jednadžbe. Duh kanonskom izgledu.

✪ Jednadžbe matematičke fizike. Shankov V.V. Proljetni semestar. Predavanje br.1

✪ Metode matematičke fizike. Tihonov Nikolaj Andrejevič (predavanje 10)

✪ 8 Parcijalnih diferencijalnih jednadžbi Mathcad

✪ Diferencijalne jednadžbe 1. Viskozno kočenje

titlovi

Uvod

Razmotrimo relativno jednostavnu parcijalnu diferencijalnu jednadžbu:

∂ ∂ y u (x , y) = 0 . (\displaystyle (\frac (\partial )(\partial y))u(x,y)=0\,.)

Problemi dokazivanja postojanja i pronalaženja rješenja sustava nelinearnih parcijalnih diferencijalnih jednadžbi rješavaju se primjenom teorije glatkih varijeteta, diferencijalne geometrije, komutativne i homološke algebre. Ove se metode koriste u fizici u proučavanju Lagrangeovog i Hamiltonovog formalizma, proučavanju viših simetrija i zakona očuvanja.

Klasifikacija

Dimenzija

Jednak broju nezavisnih varijabli. Mora biti najmanje 2 (na 1 se dobiva obična diferencijalna jednadžba).

Linearnost

Postoje linearne i nelinearne jednadžbe. Linearna jednadžba može se prikazati kao linearna kombinacija derivacija nepoznatih funkcija. Koeficijenti mogu biti ili konstante ili poznate funkcije.

Linearne jednadžbe su dobro istražene za rješavanje pojedine vrste Ne linearne jednadžbe dodijeljeni su milijunski bonusi (milenijski ciljevi).

Ujednačenost

Jednadžba je nehomogena ako postoji član koji ne ovisi o nepoznatim funkcijama.

Narudžba

Redoslijed jednadžbe određen je maksimalnim redoslijedom derivacije. Redoslijed svih varijabli je važan.

Klasifikacija linearnih jednadžbi drugog reda

Linearne parcijalne diferencijalne jednadžbe drugog reda klasificiraju se kao parabolične, eliptičke i hiperbolične.

Dvije nezavisne varijable

Linearna jednadžba drugog reda koja sadrži dvije neovisne varijable ima oblik:

A ∂ 2 u ∂ x 2 + 2 B ∂ 2 u ∂ x ∂ y + C ∂ 2 u ∂ y 2 + . . . = 0 , (\displaystyle A(\frac (\partial ^(2)u)(\partial x^(2)))+2B(\frac (\partial ^(2)u)(\partial x\partial y ))+C(\frac (\partial ^(2)u)(\partial y^(2)))+...=0,)

Gdje A, B, C- koeficijenti ovisni o varijablama x I g, a elipsa označava pojmove ovisno o x, g, u i parcijalne derivacije prvog reda: ∂ u / ∂ x (\displaystyle (\partial u)/(\partial x)) I ∂ u / ∂ y (\displaystyle (\partial u)/(\partial y)). Ova jednadžba je slična jednadžbi konusnog presjeka:

A x 2 + 2 B x y + C y 2 + ⋯ = 0. (\displaystyle Ax^(2)+2Bxy+Cy^(2)+\cdots =0.)

Kao što se stožasti presjeci dijele na elipse, parabole i hiperbole, ovisno o predznaku diskriminante D = B 2 − A C (\displaystyle D=B^(2)-AC), jednadžbe drugog reda u danoj točki se klasificiraju:

U slučaju kada su svi koeficijenti A, B, C- konstante, jednadžba ima isti tip u svim točkama u ravnini varijabli x I g. Ako su koeficijenti A, B, C kontinuirano ovisi o x I g, skup točaka u kojima je ova jednadžba hiperboličkog (eliptičnog) tipa tvori otvoreno područje na ravnini, koje se naziva hiperbolično (eliptično), a skup točaka u kojima je jednadžba paraboličkog tipa je zatvoren. Jednadžba se zove mješoviti (mješoviti tip), ako je u nekim točkama ravnina hiperbolična, a u nekim točkama eliptična. U tom slučaju parabolične točke obično tvore liniju tzv linija za promjenu tipa ili linija degeneracije.

Više od dvije nezavisne varijable

U općem slučaju, kada jednadžba drugog reda ovisi o mnogim neovisnim varijablama:

∑ i = 1 n ∑ j = 1 n a i j (x 1 , ⋯ , x n) ∂ 2 u ∂ x i ∂ x j + F (x 1 , ⋯ , x n , u , ∂ u ∂ x 1 , ⋯ , ∂ u ∂ x n) = 0 , (\displaystyle \sum _(i=1)^(n)\sum _(j=1)^(n)a_(ij)(x_(1),\cdots ,x_(n))(\ frac (\partial ^(2)u)(\partial x_(i)\partial x_(j)))+F\left(x_(1),\cdots ,x_(n),u,(\frac (\ parcijalni u)(\partial x_(1))),\cdots ,(\frac (\partial u)(\partial x_(n)))\right)=0,)

može se klasificirati u određenoj točki M 0 (x 1 0 , ⋯ , x n 0) (\displaystyle M_(0)(x_(1)^(0),\cdots ,x_(n)^(0))) analogno odgovarajućem kvadratnom obliku:

∑ i = 1 n ∑ j = 1 n a i j (x 1 0 , ⋯ , x n 0) t i t j . (\displaystyle \sum _(i=1)^(n)\sum _(j=1)^(n)a_(ij)(x_(1)^(0),\cdots ,x_(n)^( 0))t_(i)t_(j).)

Nedegeneriranom linearnom transformacijom

s i = ∑ j = 1 n A i j t j , i = 1 , 2 ⋯ n , det ‖ A i j ‖ ≠ 0 (\displaystyle s_(i)=\sum _(j=1)^(n)A_(ij)t_ (j),i=1,2\cdots n,\det \lijevo\|A_(ij)\desno\|\neq 0)

kvadratni oblik se uvijek može svesti na kanonski oblik:

∑ i = 1 n λ i s i 2 . (\displaystyle \sum _(i=1)^(n)\lambda _(i)s_(i)^(2).)

Štoviše, prema teoremu o inerciji, broj pozitivnih, negativnih i nula koeficijenata λ i (\displaystyle \lambda _(i)) u kanonskom obliku kvadratni oblik je nepromjenjiv i ne ovisi o linearnoj transformaciji. Na temelju toga se vrši klasifikacija (u točki M 0 (\displaystyle M_(0))) jednadžbe koja se razmatra:

U slučaju mnogo neovisnih varijabli, može se provesti detaljnija klasifikacija (potreba za kojom se ne javlja u slučaju dviju neovisnih varijabli):

1. Hiperbolički tip
   1. Normalni hiperbolički tip, ako je jedan koeficijent jednog predznaka, a ostali drugog.
   2. Ultrahiperbolički tip, ako postoji više od jednog koeficijenta jednog ili drugog znaka.
2. Parabolični tip mogu se dalje klasificirati u:
   1. Eliptično-parabolični tip, ako je samo jedan koeficijent jednak nuli, a ostali imaju isti predznak.
   2. Hiperbolično-parabolični tip, ako je samo jedan koeficijent jednak nuli, a ostali imaju različite predznake. Slično hiperboličnom tipu, može se podijeliti na:
      1. Normalni hiperbolično-parabolički tip
      2. Ultrahiperbolično-parabolični tip
   3. Ultraparabolični tip, ako je više od jednog koeficijenta nula. Ovdje je također moguća daljnja klasifikacija ovisno o predznacima koeficijenata koji nisu nula.

Postojanje i jedinstvenost rješenja

Iako odgovor na pitanje postojanja i jedinstvenosti rješenja obične diferencijalne jednadžbe ima potpuno iscrpan odgovor (Picard-Lindelöfov teorem), za parcijalne diferencijalne jednadžbe ne postoji jednoznačan odgovor na to pitanje. Postoji opći teorem (Cauchy-Kovalevskaya teorem) koji kaže da Cauchyjev problem za bilo koju parcijalnu diferencijalnu jednadžbu analitičku s obzirom na nepoznate funkcije i njihove izvodnice ima jedinstveno analitičko rješenje. Međutim, postoje primjeri linearnih parcijalnih diferencijalnih jednadžbi čiji koeficijenti imaju derivacije svih redova i nemaju rješenja ( Levi, ). Čak i ako rješenje postoji i jedinstveno je, ono može imati nepoželjna svojstva.

Razmotrimo niz Cauchyjevih problema (ovisno o n) za Laplaceovu jednadžbu:

∂ 2 u ∂ x 2 + ∂ 2 u ∂ y 2 = 0 , (\displaystyle (\frac (\partial ^(2)u)(\partial x^(2)))+(\frac (\partial ^( 2)u)(\djelomično y^(2)))=0,) u (x , 0) = 0 , (\displaystyle u(x,0)=0,) ∂ u ∂ y (x , 0) = sin ⁡ n x n , (\displaystyle (\frac (\partial u)(\partial y))(x,0)=(\frac (\sin nx)(n)), )

Gdje n- cijeli. Derivacija funkcije u po varijabli g ravnomjerno teži 0 x s povećanjem n, međutim, rješenje jednadžbe je

u (x, y) = (s h n y) (sin ⁡ n x) n 2. (\displaystyle u(x,y)=(\frac ((\mathrm (sh) \,ny)(\sin nx))(n^(2))).)

Rješenje teži beskonačnosti ako nx ne višestruka π (\displaystyle \pi ) za bilo koju vrijednost različitu od nule g. Cauchyjev problem za Laplaceovu jednadžbu naziva se nepravilno postavljen ili pogrešno postavljen jer ne postoji kontinuirana ovisnost rješenja o početnim podacima.

Za sustave nelinearnih parcijalnih diferencijalnih jednadžbi provode se dokazi o postojanju rješenja i traženja mnogoznačnika svih rješenja pomoću teorije glatkih mnogoznačnika, diferencijalne geometrije, komutativne i homološke algebre. Ove se metode koriste u fizici u proučavanju Lagrangeovog i Hamiltonovog formalizma, proučavanju viših simetrija i zakona očuvanja.

Primjeri

Jednodimenzionalna toplinska jednadžba

Jednadžba koja opisuje raspodjelu topline u homogenom štapu je paraboličnog tipa i ima oblik

∂ u ∂ t = α ∂ 2 u ∂ x 2 (\displaystyle (\frac (\partial u)(\partial t))=\alpha (\frac (\partial ^(2)u)(\partial x^( 2))))

Gdje u(t,x) je temperatura, a α je pozitivna konstanta koja opisuje brzinu širenja topline. Cauchyjev problem se formulira na sljedeći način:

U (0 , x) = f (x) (\displaystyle u(0,x)\,=f(x)),

Gdje f(x) je proizvoljna funkcija.

Jednadžba titranja žice

Jednadžba je hiperboličkog tipa. Ovdje u(t,x) - pomak niza iz ravnotežnog položaja, ili višak tlaka zraka u cijevi, ili veličina elektromagnetsko polje u cijevi, i c- brzina širenja valova. Da bi se formulirao Cauchyjev problem u početnom trenutku vremena, treba specificirati pomak i brzinu strune u početnom trenutku vremena:

u (0 , x) = f (x) , (\displaystyle u(0,x)=f(x),) ∂ u ∂ t (0 , x) = g (x) , (\displaystyle (\dfrac (\partial u)(\partial t))(0,x)=g(x),)

Dvodimenzionalna Laplaceova jednadžba

Odnos s analitičkim funkcijama

Realni i imaginarni dijelovi bilo koje holomorfne funkcije f (\displaystyle f) kompleksna varijabla z = x + i y (\displaystyle z=x+iy) su konjugirani harmonijski funkcije: obje zadovoljavaju Laplaceovu jednadžbu i gradijenti su im ortogonalni. Ako f=u+iv, tada Cauchy-Riemannovi uvjeti govore sljedeće:

∂ u ∂ x = ∂ v ∂ y , ∂ v ∂ x = − ∂ u ∂ y , (\displaystyle (\frac (\partial u)(\partial x))=(\frac (\partial v)(\partial y)),\quad (\frac (\partial v)(\partial x))=-(\frac (\partial u)(\partial y)),)

Zbrajajući i oduzimajući jednadžbe jedna od druge, dobivamo:

∂ 2 u ∂ x 2 + ∂ 2 u ∂ y 2 = 0 , ∂ 2 v ∂ x 2 + ∂ 2 v ∂ y 2 = 0. (\displaystyle (\frac (\partial ^(2)u)(\partial x^(2)))+(\frac (\partial ^(2)u)(\partial y^(2)))=0,\quad (\frac (\partial ^(2)v)(\partial x^(2)))+(\frac (\partial ^(2)v)(\partial y^(2)))=0.)

Također se može pokazati da je svaka harmonijska funkcija realni dio neke analitičke funkcije.

Problemi rubnih vrijednosti

Rubni problemi postavljaju se na sljedeći način: pronaći funkciju u, koja u svemu zadovoljava Laplaceovu jednadžbu unutarnje točke regija S, i na granici regije ∂ S (\displaystyle \partial S)- neki uvjet. Ovisno o vrsti uvjeta, razlikuju se sljedeći rubni problemi:

Rješavanje jednadžbi matematičke fizike

Postoje dvije vrste metoda za rješavanje ove vrste jednadžbi:

• analitički, u kojem se rezultat izvodi različitim matematičkim transformacijama;
• numerički, u kojem dobiveni rezultat odgovara stvarnom sa zadanom točnošću, ali koji zahtijeva puno rutinskih izračuna i stoga se može učiniti samo pomoću računalna tehnologija(RAČUNALO).

Analitičko rješenje

Mogu se dobiti analitička rješenja jednadžbi matematičke fizike različiti putevi. Na primjer:

• Korištenje Greenove funkcije;
• Korištenje Fourierove metode odvajanja varijabli;
• Korištenje teorije potencijala;
• Pomoću Kirchhoffove formule.

Ove metode su dizajnirane za različite vrste jednadžbe i u nekim jednostavnim slučajevima omogućuju dobivanje rješenja u obliku neke formule ili konvergentnog niza, na primjer za

Teorijski minimum

U matematičkoj fizici, kada se razmatraju problemi vezani uz rješavanje parcijalnih diferencijalnih jednadžbi drugog reda, uvijek se koncentriraju
na analizi nekih osnovnih jednadžbi: Poissonove, toplinske vodljivosti, valne jednadžbe. To je zbog mogućnosti donošenja jednadžbi drugog
reda na tzv kanonskom obliku, naime na iste upravo navedene jednadžbe.

Razmotrimo jednadžbu drugog reda opći pogled:
,
Gdje . U ovom slučaju, pretpostavit ćemo bez gubitka općenitosti da je matrica koeficijenata simetrična, tj.
(ovo je zapravo zahtjev da mješovite izvedenice budu neovisne o redoslijedu diferencijacije). U nastavku ćemo ovu matricu zvati matricom najvišeg
koeficijenti Strogo govoreći, ista jednadžba u različitim točkama može se odnositi na različiti tipovi klasifikacije. Primjer će biti dan kasnije.
U vezi s ovom napomenom, govorit ćemo o matrici vodećih koeficijenata u određenom trenutku. Pretpostavljamo da matrica vodećih koeficijenata predstavlja
je matrica nekog kvadratnog oblika. Ovaj oblik se može svesti na normalan oblik, tj. dijagonalni oblik s koeficijentima jednakim po veličini
nula ili jedan. Podsjetimo se da se broj pozitivnih koeficijenata naziva pozitivnim indeksom tromosti kvadratnog oblika, a broj negativnih
koeficijenti – negativan indeks oblika, a broj nula koeficijenata – greška oblika. Jednadžbe se mogu klasificirati pomoću njih
tri broja, koje ćemo naznačiti redom kojim su navedeni: . Zbroj ova tri broja jednak je broju nezavisnih varijabli.
Jasno je da će množenje cijele jednadžbe s minus jedan dovesti do toga da će svi elementi matrice vodećih koeficijenata promijeniti predznak. Stoga,
pozitivni i negativni indeksi odgovarajućeg oblika zamijenit će uloge. Dakle, jednadžbe pripadaju
jednoj vrsti klasifikacije.
Nabrojimo glavne klase jednadžbi:
- hiperbolično
- parabolični
- eliptični
- ultrahiperboličko
- eliptično-parabolični
Posljednje dvije vrste jednadžbi ne raspravljaju se u standardnim tečajevima.

Verbalno, ova se klasifikacija može formulirati na sljedeći način. Jednadžba je hiperbolična ako je defekt odgovarajućeg kvadratnog oblika
je jednak nuli, a jedan od indeksa je jednak jedinici. Jednadžba je parabolična ako njen oblik ima defekt jednak jedan i svi koeficijenti su istog predznaka.
Jednadžba je eliptična ako je njezin defekt oblika nula i svi koeficijenti imaju isti predznak.

Primjeri različitih vrsta jednadžbi

Primjer 1. Toplinska jednadžba.

Jednadžba paraboličnog tipa.

Primjer 2. Valna jednadžba.

Jednadžba hiperboličkog tipa.

Primjer 3. Poissonova jednadžba.

Konkretno, ako postoji nula s desne strane, tada se dobiva Laplaceova jednadžba.

Primjer 4. Helmholtzova jednadžba.

Jednadžba eliptičnog tipa.

Primjer 5. Tricomi jednadžba.

Ako je , tada je jednadžba eliptična; ako je , tada je jednadžba parabolična; ako je , onda je jednadžba hiperbolična.

Pogledajmo pobliže slučaj kada nepoznata funkcija ima samo dva argumenta:
.
Koeficijenti su funkcije varijabli i (u načelu je moguća i ovisnost o nepoznatoj funkciji (u ovom slučaju jednadžba
bit će kvazilinearan; ograničavamo se na linearne jednadžbe). Opća jednadžba može se pojednostaviti zamjenom nezavisnih varijabli -
sveden na kanonski oblik. Ovaj kanonski oblik, kao i tip zamjene, određen je karakterističnom jednadžbom
.
Karakteristična jednadžba, biće kvadratna jednadžba s obzirom na izvedenicu odmah se dijeli na dvoje.

Predznak radikalnog izraza određuje vrstu jednadžbe.

Hiperboličke jednadžbe
To je slučaj kada. Opći integrali karakteristične jednadžbe.
Zamjena u tijeku.

Parabolične jednadžbe
.
Zamjena se izvodi, gdje je proizvoljna dva puta diferencijabilna funkcija za koju
stanje .

Eliptičke jednadžbe
To je slučaj kada. Opći integral karakteristične jednadžbe . Zamjena u tijeku
.

Pogledajmo nekoliko primjera, od kojih svaki zahtijeva dovođenje jednadžbe u kanonski oblik. Tehnologija igra središnju ulogu u ovim primjerima.
zamjene varijabli, jer je navođenje same zamjene obično vrlo jednostavno. Linearna promjena varijabli izvodi se prilično jednostavno (slučaj jednadžbe s
konstantni koeficijenti).
Bilješka. Naravno, postoji određena sloboda kod zamjene varijabli. Na primjer, u svakom slučaju, zamjena se određuje točno prema znaku, koji ne igra značajnu ulogu
transformacija izvedenica. Također, u slučaju parabolične jednadžbe, dvosmislenost unosi sloboda izbora druge funkcije za zamjenu varijabli, koja je vrlo ograničena
slabi uvjeti.

Primjeri svođenja jednadžbi drugog reda na kanonski oblik

Primjer 1. Slučaj linearne promjene varijabli u hiperboličkoj jednadžbi.

.
Izvorna jednadžba je dakle hiperboličkog tipa. Nalazimo opće integrale pronađenih jednadžbi:
.
Uvodimo zamjenu. Transformirajmo derivacije. U u ovom slučaju možemo pretpostaviti da funkcija ovisi o varijablama,
koji zauzvrat ovise o starim varijablama:




.

.

Primjer 2. Slučaj linearne promjene varijabli u eliptičkoj jednadžbi.

Sastavljamo karakterističnu jednadžbu:
.
Izvorna jednadžba je stoga eliptičnog tipa. Nalazimo opći integral bilo koje od pronađenih jednadžbi:
.
Uvodimo zamjenu. Izvodnice transformiramo na potpuno isti način kao što je to učinjeno u primjeru 1.



Nakon zamjene ovih derivata u izvornu jednadžbu, dobivamo
.

Primjer 3. Slučaj linearne promjene varijabli u paraboličnoj jednadžbi.

Sastavljamo karakterističnu jednadžbu:
.
Izvorna jednadžba je stoga paraboličnog tipa. Nalazimo opći integral pronađene jednadžbe:
.
Ovo pojašnjava kako se može odabrati jedna varijabla: . Druga varijabla mora biti odabrana neovisno.
Obično se odabire najjednostavniji kako ne bi komplicirali izračune. Pogledajmo dvije opcije da vidimo kako odabir druge utječe
varijable do konačnog oblika jednadžbe. Prvo stavimo. Ponovno transformiramo derivacije na isti način kao u primjeru 1.



Nakon zamjene ovih derivata u izvornu jednadžbu, dobivamo

Prethodno su razmatrane obične diferencijalne jednadžbe. Njihove odluke ovise samo o jednoj varijabli: ,
itd. U mnogim praktičnim problemima, tražene funkcije ovise o nekoliko varijabli, a jednadžbe koje opisuju takve probleme mogu sadržavati parcijalne derivacije traženih funkcija. Zovu se parcijalne diferencijalne jednadžbe.

Na primjer, mnogi problemi u mehanici kontinuuma vode do rješenja parcijalnih diferencijalnih jednadžbi. Ovdje su najčešće tražene funkcije gustoća, temperatura, napon itd., čiji su argumenti koordinate promatrane točke u prostoru, kao i vrijeme.

Kompletna matematička formulacija problema, uz diferencijalne jednadžbe, sadrži i neke dodatne uvjete. Ako se rješenje traži u ograničenom području, tada se na njegovoj granici zadaju uvjeti koji se nazivaju rubni (rubni) uvjeti. Takvi se problemi nazivaju rubnim problemima za parcijalne diferencijalne jednadžbe.

Ako je jedna od nezavisnih varijabli u problemu koji se razmatra vrijeme t, tada se postavljaju neki uvjeti (na primjer, vrijednosti potrebnih parametara) u početnom trenutku , koji se nazivaju početni uvjeti. Problem koji se sastoji od rješavanja jednadžbe pod zadanim početnim uvjetima naziva se Cauchyjev problem za parcijalnu diferencijalnu jednadžbu. U ovom slučaju problem se rješava u neograničenom prostoru i rubni uvjeti nisu navedeni.

Problemi u čijoj se formulaciji postavljaju rubni i početni uvjeti nazivaju se nestacionarni (ili mješoviti) rubni problemi. Dobivena rješenja mijenjaju se tijekom vremena.

Tako se matematički modeli fizikalnih i drugih procesa opisuju pomoću parcijalnih diferencijalnih jednadžbi. Argumenti funkcija ovih jednadžbi su prostorne koordinate
i vrijeme .

Jednadžbe prvog reda. Jednadžbe prvog reda nazivaju se i transportne jednadžbe. To se objašnjava činjenicom da takve jednadžbe opisuju procese prijenosa čestica u medijima, širenje poremećaja itd.

Njegovo rješenje je zanimljivo ne samo s praktičnog gledišta; U još većoj mjeri ova je jednadžba korisna u razvoju i proučavanju diferencialnih shema.

Pretpostavit ćemo da tražena funkcija ovisi o vremenu i jedna prostorna varijabla x. Tada se jednadžba linearnog transporta može napisati kao

.

Ovdje - brzina prijenosa.

Jednadžbe drugog reda. Linearna parcijalna diferencijalna jednadžba drugog reda je odnos između funkcije
ili
i njegove djelomične izvedenice oblika.

(1)

Ako je varijabla funkcija ovisi o I , onda se jednadžba može napisati na sljedeći način:

(2)

Ako
, onda se jednadžbe 1-2 nazivaju homogene, inače nehomogene.

Ako
, onda jednadžba (2) pripada klasi eliptičkih jednadžbi;

Ako
, onda je ovo hiperbolička jednadžba;

Ako
- parabolična jednadžba.

Kada
nema konstantan predznak, dobiva se jednadžba mješovitog tipa.

Klasične eliptičke jednadžbe uključuju:

Laplaceova jednadžba
, koji se koristi za opisivanje magnetskih i stacionarnih toplinskih polja;

Poissonova jednadžba
, koji se koristi u elektrostatici, teoriji elastičnosti i drugim znanostima;

Helmholtzova jednadžba
, opisujući ravnomjerne oscilatorne procese.

Laplaceov operator:

u jednodimenzionalnom slučaju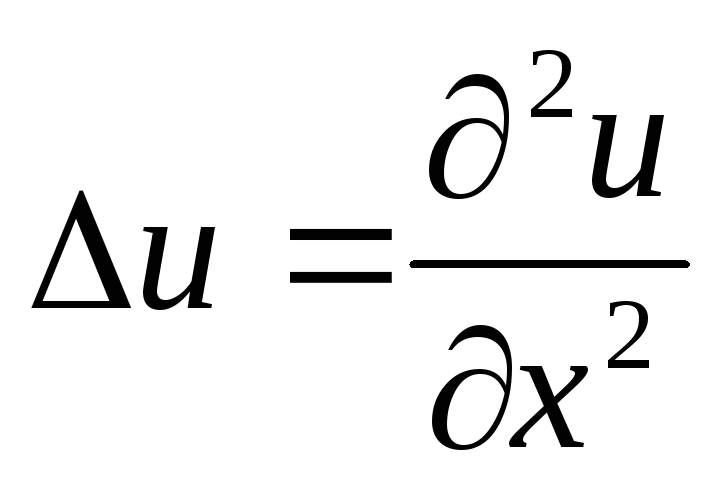
;

u dvodimenzionalnom slučaju
;

u trodimenzionalnom slučaju
.

Među hiperboličnim jednadžbama razlikujemo:

Valne jednadžbe:

jednodimenzionalni
, koji opisuje prisilne vibracije žice;

dvodimenzionalan
, koji opisuje vibracije membrane.

Telegrafska jednadžba, koja opisuje promjenu potencijala u dalekovodima. Ovdje
- koeficijent samoindukcije, kapacitet, otpor, karakteristike gubitaka po jedinici duljine voda.

Klasične parabolične jednadžbe uključuju jednadžbu topline
.

Da bi se pronašlo jedinstveno rješenje parcijalne diferencijalne jednadžbe, potrebno je odrediti početne i rubne uvjete. Početnim uvjetima obično se nazivaju uvjeti određeni u početnom trenutku vremena . Rubni uvjeti navedeni su za različite vrijednosti prostornih varijabli. Za eliptičke jednadžbe navedeni su samo rubni uvjeti koji se mogu podijeliti u tri klase:

Dirichletov uvjet
- u ovom slučaju na granici područja G u kojem se traži rješenje određena je određena kontinuirana funkcija . U jednodimenzionalnom slučaju ovaj uvjet ima oblik:
I
Gdje
- interval u kojem se traži rješenje jednodimenzionalnog problema;

Neumannovo stanje
- u ovom slučaju, na granici područja G određena je derivacija smjera vanjska normala;

Mješovito stanje
.

Za parabolične jednadžbe, osim rubnih uvjeta, potrebno je odrediti i jedan početni, koji može biti sljedeći:
.

U slučaju hiperboličkih jednadžbi, početni uvjeti mogu biti sljedeći
I
.

Rješenje niza parcijalnih diferencijalnih jednadžbi može se dobiti analitički. Jedna od najčešće korištenih metoda je metoda razdvajanja varijabli (Fourierova metoda). Pogledajmo ovu metodu detaljnije.

O metodama rješavanja parcijalnih diferencijalnih jednadžbi.

Rješavanje najjednostavnijih zadataka parcijalnih diferencijalnih jednadžbi može se provesti u nizu slučajeva analitičke metode, razmatra se u relevantnim dijelovima matematike. To se uglavnom odnosi na neke jednadžbe prvog reda, ali i na jednadžbe drugog reda s konstantnim koeficijentima. Analitičke metode korisne su ne samo zato što omogućuju dobivanje opća rješenja, koji se može koristiti više puta. Također su od velike važnosti za konstrukciju numeričkih metoda. Testiranje diferencijskih shema na poznatim rješenjima najjednostavnijih jednadžbi omogućuje procjenu tih shema i otkrivanje njihovih prednosti i slabosti.

Među numeričke metode Metode razlike se široko koriste. Oni se temelje na uvođenju određene mreže razlike u regiji koja se razmatra. Vrijednosti derivacija, početnih i rubnih uvjeta izražavaju se kroz vrijednosti funkcija u čvorovima mreže, što rezultira sustavom algebarske jednadžbe, koja se naziva shema razlike. Rješavanjem ovog sustava jednadžbi moguće je pronaći vrijednosti mrežnih funkcija u čvorovima mreže koje se približno smatraju jednakima vrijednostima traženih funkcija.

Zadane jednadžbe nazivaju se jednadžbe matematičke fizike. Mnogi primijenjeni problemi svode se na njihovo rješavanje. Prije nego prijeđemo na raspravu o numeričkim metodama za rješavanje ovih jednadžbi, razmotrimo glavna pitanja konstruiranja diferencialnih shema.

2. Uvod u grid metode, pojmove grid, predložak, sloj.

O konstrukciji diferencijskih shema. Kao što je već navedeno, konstrukcija diferencijskih shema za rješavanje parcijalnih diferencijalnih jednadžbi temelji se na uvođenju mreže u razmatrani prostor. Čvorovi mreže su projektne točke.

Primjer jednostavnog pravokutnog područja G(x, y) s granicom G u dvodimenzionalnom slučaju prikazana je na sl. 1, A. Stranice pravokutnika
,
dijele se točkama na elementarne segmente
,
I
,
. Kroz te točke povučene su dvije obitelji koordinatnih pravaca
,
tvoreći mrežu s pravokutnom ćelijom. Svaki čvor ove mreže čiji je broj (
), određena koordinatama (
).

Ab

Riža. 1. Pravokutna mreža ( A), 3D mrežasti element ( b)

Čvorovi mreže leže na granici G regije G, nazivaju se granični čvorovi. Svi ostali čvorovi su unutarnji.

Slično se uvode mreže za višedimenzionalna područja. Na sl. 1, b prikazuje mrežni element u obliku pravokutnog paralelopipeda za trodimenzionalno područje.

Uzorak– kombinacija korištenih čvorova

Budući da su početni i rubni uvjeti pri postavljanju problema formulirani na granici računske domene, može se smatrati da su navedeni na graničnim čvorovima mreže. Ponekad granične točke područja nisu čvorovi mreže, što je slučaj s područjima složenog oblika. Tada se ili uvode dodatni čvorovi na sjecištu koordinatnih linija s granicom, ili se granica približno zamjenjuje isprekidanom linijom koja prolazi kroz čvorove blizu granice. Rubni uvjeti se prenose na ovu izlomljenu liniju.

U brojnim slučajevima, složena krivuljasta područja mogu se svesti na njihov najjednostavniji oblik prelaskom na nove nezavisne varijable. Na primjer, četverokutno područje G, prikazano na sl. 2, može se svesti na jedinični kvadrat G" uvođenjem novih varijabli £, q umjesto #, y pomoću relacija

Potrebno je transformirati jednadžbe, kao i početne i rubne uvjete u nove varijable. U području G" možete unijeti pravokutnu mrežu, dok ste u području G odgovarat će mreži s neravnomjerno raspoređenim čvorovima i zakrivljenim ćelijama,

Ubuduće ćemo pri konstruiranju diferencialnih shema, radi jednostavnosti, koristiti pravokutne mreže (ili sa ćelijama u obliku pravokutnih paralelopipeda u trodimenzionalnom slučaju), a jednadžbe ćemo pisati u kartezijevim koordinatama (
). U praksi je potrebno rješavati probleme u različitim krivuljastim koordinatnim sustavima: polarnim, cilindričnim, sfernim itd. Na primjer, ako je pogodno definirati područje izračuna u polarnim koordinatama (
), tada se mreža uvodi u koracima
I
prema radijus vektoru i polarnom kutu.

Ponekad se u jednostavnu računsku domenu uvodi neuniformna mreža. Konkretno, u nekim slučajevima potrebno je poboljšati čvorove za točnije izračune u nekim dijelovima regije koja se razmatra. Pri tome su područja koncentracije čvorova ili unaprijed poznata ili se određuju u procesu rješavanja problema (npr. ovisno o gradijentima traženih funkcija).

Za konstruiranje diferencijske sheme, kao u slučaju običnih diferencijalnih jednadžbi, parcijalne derivacije u jednadžbi zamjenjuju se relacijama konačnih razlika prema određenom predlošku (vidi Poglavlje 3, § 1). U ovom slučaju, točne vrijednosti tražene funkcije U zamjenjuju se vrijednostima mrežne funkcije u čvorovima diferencijske mreže.

Kao primjer, konstruirat ćemo neke diferencijske sheme za rješavanje toplinske jednadžbe za zadane početne i rubne uvjete. Zapišimo problem mješovite rubne vrijednosti u obliku

,(6)

Gdje
- početna raspodjela temperature U(na t= 0);
- raspodjela temperature na krajevima segmenta koji se razmatra ( x= 0, 1) u bilo kojem trenutku t. Imajte na umu da početni i rubni uvjeti moraju biti dosljedni, tj.

Uvedimo uniformnu pravokutnu mrežu pomoću koordinatnih linija
,
I
,
,I - odnosno, koraci mreže u smjerovima x I t. Označavamo vrijednosti funkcije u čvorovima mreže
. Zamijenit ćemo te vrijednosti s odgovarajućim vrijednostima mrežne funkcije koji zadovoljavaju diferencijsku shemu.

Zamjenom parcijalnih derivacija željene funkcije u izvornoj jednadžbi (6) koristeći relacije konačnih razlika, dobivamo diferencijsku shemu

(7)

U snimanju ovog dijagrama, predložak prikazan na slici 1 koristi se za svaki čvor. 2, A.

Za istu jednadžbu možete konstruirati različite diferencijske sheme. Konkretno, ako koristite predložak prikazan na Sl. 2, b, tada umjesto (7) dobivamo diferencijsku shemu

(8)

U oba slučaja dobiva se sustav algebarskih jednadžbi za određivanje vrijednosti mrežne funkcije u unutarnjim čvorovima. Vrijednosti u graničnim čvorovima nalaze se iz rubnih uvjeta

Skup čvorova na t= const, tj. za fiksnu vrijednost , nazvao sloj. Shema (7) omogućuje sekvencijalno pronalaženje vrijednosti
,
na
sloju kroz odgovarajuće vrijednosti na th sloj. Takve se sheme nazivaju očito.

Za početak brojanja j= 1, potrebno je rješenje na početnom sloju. Određuje se početnim stanjem

Za razliku od eksplicitne sheme, svaka diferencijska jednadžba (8) sadrži na svakom novom sloju vrijednosti nepoznanica u tri točke, pa je te vrijednosti nemoguće odmah odrediti preko poznatog rješenja na prethodnom sloju. Takve se sheme nazivaju implicitno. U ovom slučaju diferencijska shema (8) sastoji se od linearnih jednadžbi u tri točke, tj. svaka jednadžba sadrži nepoznatu funkciju u tri točke zadanog sloja. Takvi sustavi linearnih jednadžbi s trodijagonalnom matricom mogu se riješiti metodom pomicanja, zbog čega će se pronaći vrijednosti mrežne funkcije u čvorovima.

Imajte na umu da u razmatranom primjeru dobivamo dvoslojni sklopovi, kada svaka diferentna jednadžba uključuje vrijednosti funkcije iz dva sloja - donjeg, na kojem je rješenje već pronađeno, i gornjeg, u čijim čvorovima se traži rješenje.

Korištenjem razmatrane metode konstruiranja diferencijskih shema, kada se pojedinačne parcijalne derivacije uključene u jednadžbu zamijene relacijama konačnih razlika za mrežnu funkciju (ili mrežne izraze), višeslojne sheme, kao i sheme visokog reda točnosti, mogu se stvorio.

Laplaceova jednadžba. Mnogi stacionarni fizikalni problemi (proučavanje potencijalnih tokova fluida, određivanje oblika opterećene membrane, problemi toplinske vodljivosti i difuzije u stacionarnim slučajevima itd.) svode se na rješavanje jednadžbe Poisson ljubazan

1

Ako
, tada se ova jednadžba naziva jednadžba Laplace. Radi jednostavnosti, razmotrit ćemo dvodimenzionalnu Laplaceovu jednadžbu

2

Rješenje ove jednadžbe tražit ćemo za određeno ograničeno područje G promjene nezavisnih varijabli x, y. Granica regije G je zatvorena linija L. Za potpuno formuliranje rubnog problema potrebno je osim Laplaceove jednadžbe zadati i rubni uvjet na rubu L. Uzmimo to u obliku

3

Problem koji se sastoji od rješavanja Laplaceove (ili Poissonove) jednadžbe za zadane vrijednosti željene funkcije na granici računske domene naziva se Dirichletov problem.

Jedan od načina rješavanja stacionarnih eliptičkih problema, uključujući rubne probleme, jest njihovo svođenje na rješenje nekog fiktivnog nestacionarnog problema (hiperboličkog ili paraboličkog), čije se rješenje nalazi za dovoljno velike vrijednosti t blizu rješenja izvornog problema. Ovo rješenje se zove način uspostavljanja.

Jer rješenje U(x,y) naše jednadžbe (2) ne ovisi o vremenu, tada ovoj jednadžbi možemo dodati član jednak nuli (za točno rješenje) . Tada će jednadžba (2) poprimiti oblik

4

To je jednadžba provođenja topline koja nam je poznata, za koju su diferencijske sheme već konstruirane. Ostaje samo postaviti početni uvjet. Može se uzeti u gotovo proizvoljnom obliku, u skladu s rubnim uvjetima. Stavimo

5

Rubni uvjet (3) ostaje stacionaran, tj. neovisan o vremenu.

Proces numeričkog rješavanja jednadžbe (4) uz uvjete (3), (5) sastoji se u prijelazu pri
od proizvoljne vrijednosti (5) do željenog stacionarnog rješenja. Brojanje se provodi sve dok otopina ne postigne stacionarni način rada. Naravno, ograničeni smo na rješavanje za neke dovoljno velike , ako se tražene vrijednosti na dva uzastopna sloja podudaraju s danim stupnjem točnosti.

Metoda uspostavljanja zapravo predstavlja iterativni proces rješavanja problema, a pri svakoj se iteraciji vrijednosti željene funkcije dobivaju numeričkim rješavanjem nekog pomoćnog problema.

Da biste riješili Dirichletov problem, također možete konstruirati diferencijsku shemu aproksimacijom jednadžbe (2). Uvedimo mrežu u pravokutno područje G pomoću koordinatnih linija x= const i y = const. Radi jednostavnosti, prihvatimo vrijednosti koraka u varijablama x I na jednak h(pretpostavlja se da su stranice regije G sumjerljive). Vrijednosti funkcije U u čvorovima
zamijenite vrijednostima mrežne funkcije . Zatim, aproksimirajući druge derivacije u jednadžbi (2) koristeći relacije konačnih razlika, dobivamo jednadžbu razlike (predložak je prikazan na slici):

(6)

Ova se jednadžba može prikazati kao sustav linearnih algebarskih jednadžbi u vezi s vrijednostima mrežne funkcije u čvorovima. Ovaj sustav se može napisati u obliku

Vrijednosti mrežne funkcije u čvorovima koji se nalaze na granici računske domene mogu se pronaći iz rubnog uvjeta (3):

U teoriji diferencijskih shema dokazuje se da rješenje konstruiranog diferencijskog problema postoji, a da je sama shema stabilna.

Svaka jednadžba sustava (7) (osim onih koje odgovaraju čvorovima koji se nalaze u blizini granica) sadrži pet nepoznanica. Jedna od najčešćih metoda za rješavanje ovog sustava linearnih jednadžbi je metoda iteracije. Svaku od jednadžbi pišemo u dopuštenom obliku u odnosu na vrijednost u središnjem čvoru (vidi sliku):

Proces iteracije kontrolira se maksimalnim odstupanjem M vrijednosti mrežne funkcije u čvorovima za dvije uzastopne iteracije. Ako njegova vrijednost dosegne neki zadani mali broj , ponavljanja prestaju.

Rješavanje Laplaceove jednadžbe u Mathcadu. Mathcad nudi ugrađene funkcije za rješavanje Laplaceovih i Poissonovih jednadžbi opustiti I višemrežni .

3. Rješavanje parcijalnih diferencijalnih jednadžbi metodom konačnih razlika.

4. Rješavanje eliptičkih, paraboličkih i hiperboličkih jednadžbi.

5. Nestacionarni problemi.

6. Konstrukcija eksplicitne i implicitne diferencijske sheme za jednodimenzionalnu toplinsku jednadžbu.

7. Pitanja aproksimacije, stabilnosti i konvergencije.

8. Metoda trčanja.

9. Aproksimacija parcijalnih diferencijalnih jednadžbi sustavom običnih diferencijalnih jednadžbi (direktna metoda).

10. Stacionarni problemi, diferencijske sheme, proračun za uspostavljanje.

11. Varijacijsko-diferencijske metode.

12. Metoda konačnih elemenata.