Главная / Натяжные потолки

Перемножение дробей с разными знаменателями. Умножение простых и смешанных дробей с разными знаменателями

Умножение целого числа на дробь – несложная задача. Но есть тонкости, в которых вы, наверняка, разбирались в школе, но с тех пор забыли.

Как умножить целое число на дробь – немного терминов

Если вы помните, что такое числитель, знаменатель и чем отличается правильная дробь от неправильной – пропустите этот абзац. Он для тех, кто совсем забыл теорию.

Числитель – это верхняя часть дроби – то, что делим. Знаменатель – нижняя. Это то, на что делим.
Правильная дробь та, у которой числитель меньше знаменателя. Неправильной называется дробь, у которой числитель больше или равен знаменателю.

Как умножить целое число на дробь

Правило умножения целого числа на дробь очень простое – умножаем числитель на целое, а знаменатель не трогаем. Например: два умножить на одну пятую – получаем две пятых. Четыре умножить на три шестнадцатых – получится двенадцать шестнадцатых.

Сокращение

Во втором примере полученную дробь можно сократить.
Что это значит? Обратите внимание – и числитель, и знаменатель этой дроби делятся на четыре. Разделить оба числа на общий делитель и называется – сократить дробь. Получим три четвертых.

Неправильные дроби

Но, предположим, мы умножили четыре на две пятых. Получилось восемь пятых. Это неправильная дробь.
Её обязательно нужно привести к правильному виду. Для это нужно выделить из нее целую часть.
Здесь нужно использовать деление с остатком. Получаем единицу и три в остатке.
Одна целая и три пятых и есть наша правильная дробь.

Привести к правильному виду тридцать пять восьмых – задача чуть посложнее.Самое близкое к тридцати семи число, которое делится на восемь – это тридцать два. При делении получим четыре. Отнимем от тридцати пяти тридцать два – получим три. Итог: четыре целых и три восьмых.

Равенство числителя и знаменателя. А тут все очень просто и красиво. При равенстве числителя и знаменателя получается просто единица.

Умножение обыкновенных дробей

Рассмотрим пример.

Пусть на тарелке лежит $\frac{1}{3}$ часть яблока. Нужно найти $\frac{1}{2}$ часть от нее. Необходимая часть является результатом умножения дробей $\frac{1}{3}$ и $\frac{1}{2}$. Результат умножения двух обыкновенных дробей -- это обыкновенная дробь.

Умножение двух обыкновенных дробей

Правило умножения обыкновенных дробей:

Результатом умножения дроби на дробь является дробь, числитель которой равен произведению числителей умножаемых дробей, а знаменатель равен произведению знаменателей:

Пример 1

Выполнить умножение обыкновенных дробей $\frac{3}{7}$ и $\frac{5}{11}$.

Решение.

Воспользуемся правилом умножения обыкновенных дробей:

\[\frac{3}{7}\cdot \frac{5}{11}=\frac{3\cdot 5}{7\cdot 11}=\frac{15}{77}\]

Ответ: $\frac{15}{77}$

Если в результате умножения дробей получается сократимая или неправильная дробь, то нужно ее упростить.

Пример 2

Выполнить умножение дробей $\frac{3}{8}$ и $\frac{1}{9}$.

Решение.

Используем правило умножения обыкновенных дробей:

\[\frac{3}{8}\cdot \frac{1}{9}=\frac{3\cdot 1}{8\cdot 9}=\frac{3}{72}\]

В результате получили сократимую дробь (по признаку деления на $3$. Числитель и знаменатель дроби разделим на $3$, получим:

\[\frac{3}{72}=\frac{3:3}{72:3}=\frac{1}{24}\]

Краткое решение:

\[\frac{3}{8}\cdot \frac{1}{9}=\frac{3\cdot 1}{8\cdot 9}=\frac{3}{72}=\frac{1}{24}\]

Ответ: $\frac{1}{24}.$

При умножении дробей сокращать числители и знаменатели можно до нахождения их произведения. При этом числитель и знаменатель дроби раскладывается на простые множители, после чего сокращаются повторяющиеся множители и находится результат.

Пример 3

Вычислить произведение дробей $\frac{6}{75}$ и $\frac{15}{24}$.

Решение.

Воспользуемся формулой умножения обыкновенных дробей:

\[\frac{6}{75}\cdot \frac{15}{24}=\frac{6\cdot 15}{75\cdot 24}\]

Очевидно, что в числителе и знаменателе есть числа, которые попарно можно сократить на числа $2$, $3$ и $5$. Разложим числитель и знаменатель на простые множители и произведем сокращение:

\[\frac{6\cdot 15}{75\cdot 24}=\frac{2\cdot 3\cdot 3\cdot 5}{3\cdot 5\cdot 5\cdot 2\cdot 2\cdot 2\cdot 3}=\frac{1}{5\cdot 2\cdot 2}=\frac{1}{20}\]

Ответ: $\frac{1}{20}.$

При умножении дробей можно применять переместительный закон:

Умножение обыкновенной дроби на натуральное число

Правило умножения обыкновенной дроби на натуральное число:

Результатом умножения дроби на натуральное число является дробь, у которой числитель равен произведению числителя умножаемой дроби на натуральное число, а знаменатель равен знаменателю умножаемой дроби:

где $\frac{a}{b}$ -- обыкновенная дробь, $n$ -- натуральное число.

Пример 4

Выполнить умножение дроби $\frac{3}{17}$ на $4$.

Решение.

Воспользуемся правилом умножения обыкновенной дроби на натуральное число:

\[\frac{3}{17}\cdot 4=\frac{3\cdot 4}{17}=\frac{12}{17}\]

Ответ: $\frac{12}{17}.$

Не стоит забывать о проверке результата умножения на сократимость дроби или на неправильную дробь.

Пример 5

Умножить дробь $\frac{7}{15}$ на число $3$.

Решение.

Воспользуемся формулой умножения дроби на натуральное число:

\[\frac{7}{15}\cdot 3=\frac{7\cdot 3}{15}=\frac{21}{15}\]

По признаку деления на число $3$} можно определить, что полученную дробь можно сократить:

\[\frac{21}{15}=\frac{21:3}{15:3}=\frac{7}{5}\]

В результате получили неправильную дробь. Выделим целую часть:

\[\frac{7}{5}=1\frac{2}{5}\]

Краткое решение:

\[\frac{7}{15}\cdot 3=\frac{7\cdot 3}{15}=\frac{21}{15}=\frac{7}{5}=1\frac{2}{5}\]

Сократить дроби также можно было заменой чисел в числителе и знаменателе на их разложения на простые множители. В таком случае решение можно было записать так:

\[\frac{7}{15}\cdot 3=\frac{7\cdot 3}{15}=\frac{7\cdot 3}{3\cdot 5}=\frac{7}{5}=1\frac{2}{5}\]

Ответ: $1\frac{2}{5}.$

При умножении дроби на натуральное число можно использовать переместительный закон:

Деление обыкновенных дробей

Операция деления является обратной к умножению и результатом ее является дробь, на которую нужно умножить известную дробь чтобы получить известное произведение двух дробей.

Деление двух обыкновенных дробей

Правило деления обыкновенных дробей: Очевидно, что числитель и знаменатель полученной дроби можно разложить на простые множители и произвести сокращение:

\[\frac{8\cdot 35}{15\cdot 12}=\frac{2\cdot 2\cdot 2\cdot 5\cdot 7}{3\cdot 5\cdot 2\cdot 2\cdot 3}=\frac{2\cdot 7}{3\cdot 3}=\frac{14}{9}\]

В результате получили неправильную дробь, из которой выделим целую часть:

\[\frac{14}{9}=1\frac{5}{9}\]

Ответ: $1\frac{5}{9}.$

В прошлый раз мы научились складывать и вычитать дроби (см. урок «Сложение и вычитание дробей »). Наиболее сложным моментом в тех действиях было приведение дробей к общему знаменателю.

Теперь настала пора разобраться с умножением и делением. Хорошая новость состоит в том, что эти операции выполняются даже проще, чем сложение и вычитание. Для начала рассмотрим простейший случай, когда есть две положительные дроби без выделенной целой части.

Чтобы умножить две дроби, надо отдельно умножить их числители и знаменатели. Первое число будет числителем новой дроби, а второе - знаменателем.

Чтобы разделить две дроби, надо первую дробь умножить на «перевернутую» вторую.

Обозначение:

Из определения следует, что деление дробей сводится к умножению. Чтобы «перевернуть» дробь, достаточно поменять местами числитель и знаменатель. Поэтому весь урок мы будем рассматривать в основном умножение.

В результате умножения может возникнуть (и зачастую действительно возникает) сократимая дробь - ее, разумеется, надо сократить. Если после всех сокращений дробь оказалась неправильной, в ней следует выделить целую часть. Но чего точно не будет при умножении, так это приведения к общему знаменателю: никаких методов «крест-накрест», наибольших множителей и наименьших общих кратных.

По определению имеем:

Умножение дробей с целой частью и отрицательных дробей

Если в дробях присутствует целая часть, их надо перевести в неправильные - и только затем умножать по схемам, изложенным выше.

Если в числителе дроби, в знаменателе или перед ней стоит минус, его можно вынести за пределы умножения или вообще убрать по следующим правилам:

Плюс на минус дает минус;
Минус на минус дает плюс.

До сих пор эти правила встречались только при сложении и вычитании отрицательных дробей, когда требовалось избавиться от целой части. Для произведения их можно обобщить, чтобы «сжигать» сразу несколько минусов:

Вычеркиваем минусы парами до тех пор, пока они полностью не исчезнут. В крайнем случае, один минус может выжить - тот, которому не нашлось пары;
Если минусов не осталось, операция выполнена - можно приступать к умножению. Если же последний минус не зачеркнут, поскольку ему не нашлось пары, выносим его за пределы умножения. Получится отрицательная дробь.

Задача. Найдите значение выражения:

Все дроби переводим в неправильные, а затем выносим минусы за пределы умножения. То, что осталось, умножаем по обычным правилам. Получаем:

Еще раз напомню, что минус, который стоит перед дробью с выделенной целой частью, относится именно ко всей дроби, а не только к ее целой части (это касается двух последних примеров).

Также обратите внимание на отрицательные числа: при умножении они заключаются в скобки. Это сделано для того, чтобы отделить минусы от знаков умножения и сделать всю запись более аккуратной.

Сокращение дробей «на лету»

Умножение - весьма трудоемкая операция. Числа здесь получаются довольно большие, и чтобы упростить задачу, можно попробовать сократить дробь еще до умножения . Ведь по существу, числители и знаменатели дробей - это обычные множители, и, следовательно, их можно сокращать, используя основное свойство дроби. Взгляните на примеры:

Задача. Найдите значение выражения:

По определению имеем:

Во всех примерах красным цветом отмечены числа, которые подверглись сокращению, и то, что от них осталось.

Обратите внимание: в первом случае множители сократились полностью. На их месте остались единицы, которые, вообще говоря, можно не писать. Во втором примере полного сокращения добиться не удалось, но суммарный объем вычислений все равно уменьшился.

Однако ни в коем случае не используйте этот прием при сложении и вычитании дробей! Да, иногда там встречаются похожие числа, которые так и хочется сократить. Вот, посмотрите:

Так делать нельзя!

Ошибка возникает из-за того, что при сложении в числителе дроби появляется сумма, а не произведение чисел. Следовательно, применять основное свойство дроби нельзя, поскольку в этом свойстве речь идет именно об умножении чисел.

Других оснований для сокращения дробей просто не существует, поэтому правильное решение предыдущей задачи выглядит так:

Правильное решение:

Как видите, правильный ответ оказался не таким красивым. В общем, будьте внимательны.

ОБОЙДИ УЖЕ ЭТИ ГРАБЛИ! 🙂

Умножение и деление дробей.

Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень. »
И для тех, кто «очень даже. »)

Эта операция гораздо приятнее сложения-вычитания! Потому что проще. Напоминаю: чтобы умножить дробь на дробь, нужно перемножить числители (это будет числитель результата) и знаменатели (это будет знаменатель). То есть:

Всё предельно просто . И, пожалуйста, не ищите общий знаменатель! Не надо его здесь…

Чтобы разделить дробь на дробь, нужно перевернуть вторую (это важно!) дробь и их перемножить, т.е.:

Если попалось умножение или деление с целыми числами и дробями — ничего страшного. Как и при сложении, делаем из целого числа дробь с единицей в знаменателе — и вперёд! Например:

В старших классах часто приходится иметь дело с трехэтажными (а то и четырехэтажными!) дробями. Например:

Как эту дробь привести к приличному виду? Да очень просто! Использовать деление через две точки:

Но не забывайте о порядке деления! В отличие от умножения, здесь это очень важно! Конечно, 4:2, или 2:4 мы не спутаем. А вот в трёхэтажной дроби легко ошибиться. Обратите внимание, например:

В первом случае (выражение слева):

Во втором (выражение справа):

Чувствуете разницу? 4 и 1/9!

А чем задается порядок деления? Или скобками, или (как здесь) длиной горизонтальных черточек. Развивайте глазомер. А если нет ни скобок, ни черточек, типа:

то делим-умножаем по порядочку, слева направо !

И еще очень простой и важный приём. В действиях со степенями он вам ох как пригодится! Поделим единицу на любую дробь, например, на 13/15:

Дробь перевернулась! И так бывает всегда. При делении 1 на любую дробь, в результате получаем ту же дробь, только перевернутую.

Вот и все действия с дробями. Вещь достаточно простая, но ошибок даёт более, чем достаточно. Примите к сведению практические советы, и их (ошибок) будет меньше!

1. Самое главное при работе с дробными выражениями — аккуратность и внимательность! Это не общие слова, не благие пожелания! Это суровая необходимость! Все вычисления на ЕГЭ делайте как полноценное задание, сосредоточенно и чётко. Лучше написать две лишние строчки в черновике, чем накосячить при расчёте в уме.

2. В примерах с разными видами дробей — переходим к обыкновенным дробям.

3. Все дроби сокращаем до упора.

4. Многоэтажные дробные выражения сводим к обыкновенным, используя деление через две точки (следим за порядком деления!).

Вот вам задания, которые нужно обязательно прорешать. Ответы даны после всех заданий. Используйте материалы этой темы и практические советы. Прикиньте, сколько примеров вы смогли решить правильно. С первого раза! Без калькулятора! И сделайте верные выводы.

Помните – правильный ответ, полученный со второго (тем более – третьего) раза – не считается! Такова суровая жизнь.

Итак, решаем в режиме экзамена ! Это уже подготовка к ЕГЭ, между прочим. Решаем пример, проверяем, решаем следующий. Решили все — проверили снова с первого по последний. И только потом смотрим ответы.

Ищем ответы, которые совпадают с вашими. Я специально их в беспорядке записал, подальше от соблазна, так сказать. Вот они, ответы, через точку с запятой записаны.

0; 17/22; 3/4; 2/5; 1; 25.

А теперь делаем выводы. Если всё получилось — рад за вас! Элементарные вычисления с дробями — не ваша проблема! Можно заняться более серьёзными вещами. Если нет.

Значит, у вас одна из двух проблем. Или обе сразу.) Нехватка знаний и (или) невнимательность. Но. Это решаемые проблемы.

В Особом разделе 555 «Дроби» разобраны все эти (и не только!) примеры. С подробными пояснениями что, зачем и как. Такой разбор здорово помогает при нехватке знаний и навыков!

Да и по второй проблеме там есть кое-что.) Вполне практический совет, как стать внимательнее . Да-да! Совет, который может применить каждый .

Кроме знаний и внимательности для успеха нужен определенный автоматизм. Где его взять? Слышу тяжелый вздох… Да, только в практике, больше негде.

Можете для тренировки зайти на сайт 321start.ru. Там в опции «Попробовать» есть 10 примеров для всех желающих. С мгновенной проверкой. Для зарегистрированных пользователей — 34 примера от простых до суровых. Это только по дробям.

Если Вам нравится этот сайт.

Кстати, у меня есть ещё парочка интересных сайтов для Вас.)

Вот здесь можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)

А вот здесь можно познакомиться с функциями и производными.

Правило 1.

Чтобы умножить дробь на натуральное число, надо ее числитель умножить на это число, а знаменатель оставить без изменения.

Правило 2.

Чтобы умножить дробь на дробь, надо:

1. найти произведение числителей и произведение знаменателей этих дробей

2. первое произведение записать числителе, а второе — знаменателем.

Правило 3.

Для того, чтобы выполнить умножение смешанных чисел, надо их записать в виде неправильных дробей, а затем воспользоваться правилом умножения дробей.

Правило 4.

Чтобы разделить одну дробь на другую, надо делимое умножить на число, обратное делителю.

Пример 1.

Вычислите

Пример 2.

Вычислите

Пример 3.

Вычислите

Пример 4.

Вычислите

Математика. Другие материалы

Возведение числа в рациональную степень. (

Возведение числа в натуральную степень. (

Обобщенный метод интервалов при решении алгебраических неравенств (Автор Колчанов А.В.)

Метод замены множителей при решении алгебраических неравенств (Автор Колчанов А.В.)

Признаки делимости (Лунгу Алена)

Проверь себя по теме ‘Умножение и деление обыкновенных дробей’

Умножение дробей

Умножение обыкновенных дробей рассмотрим в нескольких возможных вариантах.

Умножение обыкновенной дроби на дробь

Это наиболее простой случай, в котором нужно пользоваться следующими правилами умножения дробей .

Чтобы умножить дробь на дробь , надо:

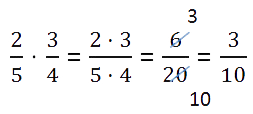
числитель первой дроби умножить на числитель второй дроби и их произведение записать в числитель новой дроби;

знаменатель первой дроби умножить на знаменатель второй дроби и их произведение записать в знаменатель новой дроби;

Прежде чем перемножать числители и знаменатели проверьте нельзя ли сократить дроби. Сокращение дробей при расчётах значительно облегчит ваши вычисления.

Умножение дроби на натуральное число

Чтобы дробь умножить на натуральное число нужно числитель дроби умножить на это число, а знаменатель дроби оставить без изменения.

Если в результате умножения получилась неправильная дробь, не забудьте превратить её в смешанное число, то есть выделить целую часть.

Умножение смешанных чисел

Чтобы перемножить смешанные числа, надо вначале превратить их в неправильные дроби и после этого умножить по правилу умножения обыкновенных дробей.

Другой способ умножения дроби на натуральное число

Иногда при расчётах удобнее воспользоваться другим способом умножения обыкновенной дроби на число.

Чтобы умножить дробь на натуральное число нужно знаменатель дроби разделить на это число, а числитель оставить прежним.

Как видно из примера, этим вариантом правила удобнее пользоваться, если знаменатель дроби делится без остатка на натуральное число.

Деление дроби на число

Как разделить дробь на число быстрее всего? Разберем теорию, сделаем вывод и на примерах посмотрим, как деление дроби на число можно выполнять по новому короткому правилу.

Обычно деление дроби на число выполняют по правилу деления дробей. Первое число (дробь) умножаем на число, обратное второму. Поскольку второе число целое, обратное к нему число - дробь, числитель которой равен единице, а знаменатель - данному числу. Схематически деление дроби на натуральное число выглядит так:

Отсюда делаем вывод:

чтобы разделить дробь на число, надо знаменатель умножить на это число, а числитель оставить прежним. Правило можно сформулировать еще короче:

при делении дроби на число число идет в знаменатель.

Выполнить деление дроби на число:

Чтобы разделить дробь на число, числитель перепишем без изменений, а знаменатель умножим на это число. Сокращаем 6 и 3 на 3.

При делении дроби на число числитель переписываем, а знаменатель умножаем на это число. Сокращаем 16 и 24 на 8.

При делении дроби на число число идет в знаменатель, поэтому числитель оставляем таким же, а знаменатель умножаем на делитель. Сокращаем 21 и 35 на 7.

Умножение и деление дробей

В прошлый раз мы научились складывать и вычитать дроби (см. урок «Сложение и вычитание дробей»). Наиболее сложным моментом в тех действиях было приведение дробей к общему знаменателю.

Чтобы умножить две дроби, надо отдельно умножить их числители и знаменатели. Первое число будет числителем новой дроби, а второе - знаменателем.

Чтобы разделить две дроби, надо первую дробь умножить на «перевернутую» вторую.

Задача. Найдите значение выражения:

По определению имеем:

Умножение дробей с целой частью и отрицательных дробей

Плюс на минус дает минус;
Минус на минус дает плюс.

Вычеркиваем минусы парами до тех пор, пока они полностью не исчезнут. В крайнем случае, один минус может выжить - тот, которому не нашлось пары;
Если минусов не осталось, операция выполнена - можно приступать к умножению. Если же последний минус не зачеркнут, поскольку ему не нашлось пары, выносим его за пределы умножения. Получится отрицательная дробь.

Сокращение дробей «на лету»

Во всех примерах красным цветом отмечены числа, которые подверглись сокращению, и то, что от них осталось.

Так делать нельзя!

Как видите, правильный ответ оказался не таким красивым. В общем, будьте внимательны.

Деление дробей.

Деление дроби на натуральное число.

Примеры деления дроби на натуральное число

Деление натурального числа на дробь.

Примеры деления натурального числа на дробь

Деление обыкновенных дробей.

Примеры деления обыкновенных дробей

Деление смешанных чисел.

преобразовать смешанные дроби в неправильные;
умножить первую дробь на дробь, обратную второй;
сократить полученную дробь;
если получилась неправильная дробь преобразовать неправильную дробь в смешанную.

Примеры деления смешанных чисел

1 1 2: 2 2 3 = 1 · 2 + 1 2: 2 · 3 + 2 3 = 3 2: 8 3 = 3 2 · 3 8 = 3 · 3 2 · 8 = 9 16

2 1 7: 3 5 = 2 · 7 + 1 7: 3 5 = 15 7: 3 5 = 15 7 · 5 3 = 15 · 5 7 · 3 = 5 · 5 7 = 25 7 = 7 · 3 + 4 7 = 3 4 7

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool .
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Дроби. Умножение и деление дробей.

Умножение обыкновенной дроби на дробь.

Чтобы перемножить обыкновенные дроби, необходимо умножить числитель на числитель (получим числитель произведения) и знаменатель на знаменатель (получим знаменатель произведения).

Формула умножения дробей:

Перед тем, как приступить к умножению числителей и знаменателей, необходимо проверить на возможность сокращения дроби. Если получится сократить дробь, то вам легче будет дальше производить расчеты.

Обратите внимание! Здесь не нужно искать общий знаменатель!!

Деление обыкновенной дроби на дробь.

Деление обыкновенной дроби на дробь происходит так: переворачиваете вторую дробь (т.е. меняете числитель и знаменатель местами) и после этого дроби перемножаются.

Формула деления обыкновенных дробей:

Умножение дроби на натуральное число.

Обратите внимание! При умножении дроби на натуральное число, числитель дроби умножается на наше натуральное число, а знаменатель дроби оставляем прежним. Если результатом произведения оказалась неправильная дробь, то обязательно выделите целую часть, превратив неправильную дробь в смешанную.

Деление дробей с участием натурального числа.

Это не так страшно, как кажется. Как и в случае со сложением, переводим целое число в дробь с единицей в знаменателе. Например:

Умножение смешанных дробей.

Правила умножения дробей (смешанных):

преобразовываем смешанные дроби в неправильные;
перемножаем числители и знаменатели дробей;
сокращаем дробь;
если получили неправильную дробь, то преобразовываем неправильную дробь в смешанную.

Обратите внимание! Чтобы умножить смешанную дробь на другую смешанную дробь, нужно, для начала, привести их к виду неправильных дробей, а далее умножить по правилу умножения обыкновенных дробей.

Второй способ умножения дроби на натуральное число.

Бывает более удобно использовать второй способ умножения обыкновенной дроби на число.

Обратите внимание! Для умножения дроби на натуральное число необходимо знаменатель дроби разделить на это число, а числитель оставить без изменения.

Из, приведенного выше, примера понятно, что этот вариант удобней для использования, когда знаменатель дроби делится без остатка на натуральное число.

Многоэтажные дроби.

В старших классах зачастую встречаются трехэтажные (или больше) дроби. Пример:

Чтобы привести такую дробь к привычному виду, используют деление через 2 точки:

Обратите внимание! В делении дробей очень важен порядок деления. Будьте внимательны, здесь легко запутаться.

Обратите внимание, например:

При делении единицы на любую дробь, результатом будет таже самая дробь, только перевернутая:

Практические советы при умножении и делении дробей:

1. Самым важным в работе с дробными выражениями является аккуратность и внимательность. Все вычисления делайте внимательно и аккуратно, сосредоточенно и чётко. Лучше запишите несколько лишних строчек в черновике, чем запутаться в расчетах в уме.

2. В заданиях с разными видами дробей — переходите к виду обыкновенных дробей.

3. Все дроби сокращаем до тех пор, пока сокращать уже будет невозможно.

4. Многоэтажные дробные выражения приводим в вид обыкновенных, пользуясь делением через 2 точки.

Недо- и не до- Переделанная песня "Весеннее танго" (Приходит время - птицы с юга прилетают) - муз. Валерий Миляев Недослышал, недопонял, недогнал, в смысле том, что я не догадался, все глаголы с не раздельно написал, о приставке недо- я не знал. Бывает так, […]
Страница не найдена В третьем окончательном чтении был принят пакет документов Правительства, предусматривающих создание специальных административных районов (САР). Вследствие выхода из Евросоюза, Великобритания не будет включена в Европейскую зону НДС и […]
Объединенный следственный комитет появится уже осенью Объединенный следственный комитет появится уже осенью Следствие всех силовых структур соберут под одной крышей с четвертой попытки Уже осенью 2014-го, по данным «Известий», президент Владимир Путин […]
Патент на алгоритм Как патент на алгоритм выглядит Как патент на алгоритм готовится Подготовка технических описаний способов хранения, обработки, и передачи, сигналов и/или данных именно для целей патентования особых сложностей обычно не представляет, и […]
ЧТО ВАЖНО ЗНАТЬ О НОВОМ ЗАКОНОПРОЕКТЕ О ПЕНСИЯХ 12 декабря 1993 года КОНСТИТУЦИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ (с учетом поправок, внесенных Законами Российской Федерациио поправках к Конституции Российской Федерацииот 30.12.2008 N 6-ФКЗ, от 30.12.2008 N 7-ФКЗ,от […]
Частушки про пенсию женщине прикольные для юбиляра мужчины для юбиляра мужчины - хором для юбиляра женщины - посвящение в пенсионеры женщины шуточное Будут интересны конкурсы для пенсионеров Ведущий: Дорогие друзья! Минутку внимания! Сенсация! Только […]