Статистическая значимость. Достоверность статистическая

Рассмотрим типичный пример применения статистических методов в медицине. Создатели препарата предполагают, что он увеличивает диурез пропорционально принятой дозе. Для проверки этого предположения они назначают пяти добровольцам разные дозы препарата.

По результатам наблюдений строят график зависимости диуреза от дозы (рис. 1.2А). Зависимость видна невооруженным глазом. Исследователи поздравляют друг друга с открытием, а мир - с новым диуретиком.

На самом деле данные позволяют достоверно утверждать лишь то, что зависимость диуреза от дозы наблюдалась у этих пяти добровольцев. То, что эта зависимость проявится у всех людей, которые будут принимать препарат, - не более чем предполо-
зЯ

с

жение. Нельзя сказать, что оно беспочвенно - иначе, зачем ставить эксперименты?

Но вот препарат поступил в продажу. Все больше людей принимают его в надежде увеличить свой диурез. И что же мы видим? Мы видим рис 1.2Б, который свидетельствует об отсутствии какой либо связи между дозой препарата и диурезом. Черными кружками отмечены данные первоначального исследования. Статистика располагает методами, позволяющими оценить вероятность получения столь «непредставительной», более того, сбивающей с толку выборки. Оказывается в отсутствие связи между диурезом и дозой препарата полученная «зависимость» наблюдалась бы примерно в 5 из 1000 экспериментов. Итак, в данном случае исследователям просто не повезло. Если бы они применили даже самые совершенные статистические методы, это все равно не спасло бы их от ошибки.

Этот вымышленный, но совсем не далекий от реальности пример, мы привели не для того, чтобы указать на бесполез
ность статистики. Он говорит о другом, о вероятностном характере ее выводов. В результате применения статистического метода мы получаем не истину в последней инстанции, а всего лишь оценку вероятности того или иного предположения. Кроме того, каждый статистический метод основан на собственной математической модели и результаты его правильны настолько насколько эта модель соответствует действительности.

Еще по теме ДОСТОВЕРНОСТЬ И СТАТИСТИЧЕСКАЯ ЗНАЧИМОСТЬ:

1. Статистически значимые отличия показателей качества жизни
2. Статистическая совокупность. Учетные признаки. Понятие о сплошных и выборочных исследованиях. Требования к статистической совокупности и использованию учетно-отчетных документов
3. РЕФЕРАТ. ИССЛЕДОВАНИЕ ДОСТОВЕРНОСТИ ПОКАЗАНИЙ ТОНОМЕТРА ДЛЯ ИЗМЕРЕНИЯ ВНУТРИГЛАЗНОГО ДАВЛЕНИЯ ЧЕРЕЗ ВЕКО2018, 2018

Совсем недавно Владимир Давыдов написал пост в facebook про A/B- или MVT-тестирование, который вызвал массу вопросов.

Обычно проведение A/B- или MVT-тестирований на сайтах — вещь очень сложная. Хотя «посадочникам» кажется, что это элементарно, ведь «этсамое, есть же специальные программы, гыг».

Если вы решили тестировать веб-содержимое, помните:

1. Для начала нужно изолировать равнозначную, равновеликую, равнокачественную аудиторию. Провести A/A-тесты. Подавляющее большинство тестов, которые проводят агентства на потоке или неопытные интернет-маркетологи, не верны. Именно по той причине, что тестируется содержимое на разных аудиториях.

2. Проводите десятки или лучше сотни тестов в течение нескольких месяцев. Тестировать недельку 2-3 варианта странички не стоит.

3. Помните, что тестировать можно и в формате MVT (то есть много вариантов), а не только A и B.

4. Статистически проанализируйте массив данных с результатами тестов (в Excel абсолютно окей, можно ещё SPSS использовать). Находятся ли результаты в рамках погрешности, насколько сильно отклоняются и как зависят от времени. Если, например, в первом пункте A/A-теста вы получили сильные отклонения одного варианта от другого — это провал, и дальше тестировать нельзя.

5. Не надо тестировать все подряд. Это не развлечение (только если вам реально больше нечего делать). Тестировать имеет смысл только то, что с точки зрения маркетингового и бизнес-анализа способно привести к заметным результатам. А также то, результат от чего можно реально измерить. Например, вы решили увеличить размер шрифта на сайте, потестировали пару недель страницу с большим шрифтом — продажи выросли. О чем это говорит? Вот и мне ни о чем (см. предыдущие пункты).

6. Тестировать нужно пути целиком. То есть недостаточно взять и протестировать страницу покупки (или какого-то действия на сайте) — нужно тестировать и те страницы и шаги, которые подводят к этой финальной конверсионной странице.

В комментариях был задан вопрос:

«Как устанавливать победителя? Вот протестировали мы заголовок на странице, продающей «в лоб». Какая разница в конверсии должна быть между А и B, чтобы признать победителя?»

Ответ Владимира:

Во-первых, нужно проводить длительные изолированные эксперименты (базовое правило любой статистической оценки). Во-вторых, все неминуемо сводится к статистике и математике (поэтому и рекомендую excel и spss или аналоги бесплатные) Нам нужно посчитать доверительную вероятность того, что разница в значениях чего-то значит. Есть хорошая статья (одна из многих). Там берут транзакции из GA по проводимым Optimizely-тестам https://www.distilled.net/uploads/ga_transactions.png , сравнивают транзакции (покупки) обычным колокольным распределением и смотрят, попадает ли среднее значение в рамки доверительного интервала погрешности https://www.distilled.net/uploads/t-test_tool.png

Хотите получить предложение от нас?

Начать сотрудничество

Роль статистической значимости при повышении конверсии: 6 вещей, которые нужно знать

1. Именно то, что это значит

«Изменение позволило достичь повышения конверсии на 20% с доверительной вероятностью 90%». К сожалению, это утверждение вовсе не равнозначно другому, очень похожему: «Шансы повысить конверсию на 20% составляют 90%». Так о чем же речь на самом деле?

20% — это рост, который мы зафиксировали по результатам тестов на одном из образцов. Если бы мы начали фантазировать и строить догадки, мы бы могли предположить, что этот рост может сохраняться постоянно – если мы будем продолжать тестирование до бесконечности. Но это никак не означает, что с вероятностью 90% мы получим двадцатипроцентный рост конверсии или рост «как минимум» в 20%, или «приблизительно» в 20%.

90% — это вероятность проявления каких бы то ни было изменений в конверсии. Другими словами, если бы мы проводили десять А/B-тестов, чтобы получить этот результат, и решили бы проводить все десять до бесконечности, то один из них (так как вероятность изменений 90%, то 10% остаётся на неизменный исход), вероятно, закончился бы приближением результата «после теста» к первоначальной конверсии – то есть, без изменений. Из остающихся девяти тестов некоторые могли бы показать рост, составляющий куда меньше 20%. В других результат мог бы превысить эту планку.

Если неверно интерпретировать эти данные, мы сильно рискуем, «выкатывая» тест. Легко обрадоваться, когда тест показывает высокие показатели роста конверсии с доверительной вероятностью в 95%, но мудрее было бы не ожидать слишком многого, пока тест не доведен до логического завершения.

2. Когда использовать

Самые очевидные кандидаты – сплит-тесты «А/В», но они далеко не единственные. Можно также проводить тестирование статистически значимой разницы между сегментами (например, посещениями через обычный и через оплаченный поиск) или временными промежутками (например, апрелем 2013 года и апрелем 2014 года).

Однако стоит заметить, что эта корреляция не подразумевает причинно-следственную связь. Проводя сплит-тесты, мы знаем, что можем приписать любые изменения результатов тем элементам, которыми различаются страницы – ведь особое внимание уделяется тому, чтобы в остальном страницы были совершенно идентичны. Если вы сравниваете такие группы, как посетители, пришедшие из обычного и платного поиска, сработать могут любые другие факторы – к примеру, из обычного поиска может быть много посещений по ночам, а конверсия среди ночных посетителей весьма высока. Тесты на значимость помогают установить, есть ли у изменений причина, но они не смогут сказать, в чем именно она заключается.

3. Как тестировать изменения показателей конверсии, отказов и выходов (exit rate)

Когда мы смотрим на «показатели», на самом деле мы видим усредненные значения двоичных переменных – кто-то либо выполнил целевые действия, либо нет. Если у нас есть выборка в 10 человек с показателем конверсии в 40%, на самом деле мы смотрим на подобную таблицу:

Эта таблица потребуется нам вкупе со средним показателем, чтобы вычислить среднее отклонение – ключевой компонент статистической значимости. Однако тот факт, что каждое значение в таблице является либо нулем, либо единицей, облегчает нам задачу – мы можем обойтись без необходимости копировать огромный список цифр, воспользовавшись калькулятором для подсчета доверительной вероятности А/B-тестов, и отталкиваясь от знания среднего показателя и размеров выборки. Это инструмент от KissMetrics .

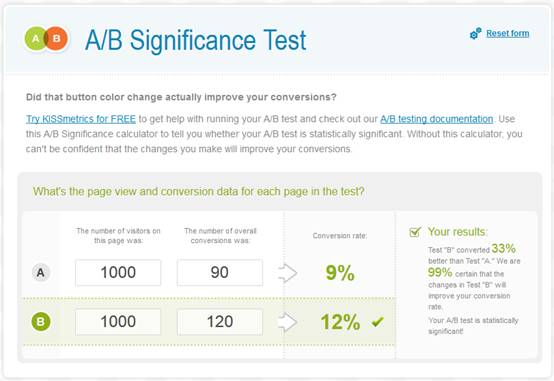
(Важно! Этот инструмент в расчетах принимает во внимание только одну сторону “колокола” распределения вероятности . Чтобы использовать обе стороны и перевести результат в двустороннюю значимость, нужно удвоить дистанцию от 100% — например, односторонние 95% становятся двусторонними 90%).

Несмотря на то, что в описании значится «инструмент тестирования достоверности А/B-тестов», его также можно использовать для любого другого сравнения показателей – просто замените конверсию на показатель отказов или выходов. Кроме того, его можно использовать и для сравнения сегментов или промежутков времени – вычисления будут те же.

Также, он хорошо подходит для мультивариантных тестирований (MVT) – просто сравнивайте с оригиналом каждое изменение по отдельности.

4. Как тестировать изменения среднего чека

Чтобы тестировать средние значение недвоичных переменных, нам потребуется полный набор данных, так что здесь все немного сложнее. Например, мы хотим установить, есть ли значимые различия средней суммы заказа для сплит-теста А/В – этот момент часто опускают при оптимизации конверсии, хотя для бизнес-показателей он так же важен, как и сама конверсия.

Первое, что нам нужно, это получить из Google Analytics полный список транзакций для каждого варианта теста — для А и B (было, стало). Простейший способ это сделать – создать пользовательские сегменты, базирующиеся на переменных (custom variables) для вашего сплит-теста, а затем экспортировать отчет по транзакциям в таблицу Excel. Убедитесь, что туда войдут все транзакции, а не только 10 строк, указанных по умолчанию.

Когда у вас есть два списка транзакций, их можно скопировать в подобный инструмент :

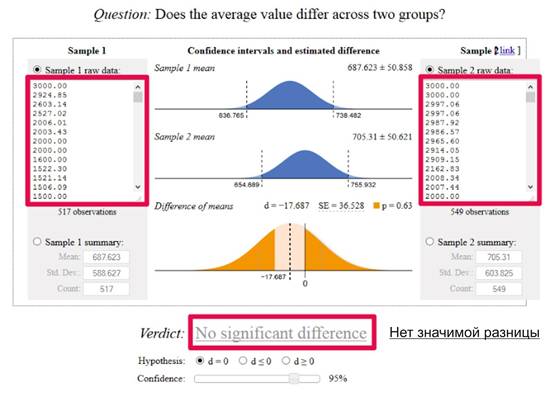
В вышеозначенном случае у нас нет доверительной вероятности на выбранном уровне в 95%. На самом деле, если мы взглянем на показатель «p» над нижним графиком, составляющий 0,63, станет ясно, что у нас нет даже 50% значимости – существует вероятность в 63%, что разница между показателями страниц является чистой случайностью.

5. Как предугадать необходимую продолжительность сплит-теста А/В

На Evanmiller.org есть еще один удобный инструмент для оптимизации конверсии – калькулятор размера выборки .

Этот инструмент позволяет дать ответ на вопрос «Сколько потребуется времени, чтобы получить достоверные результаты теста?», и этот ответ не стоит пытаться угадать.

Стоит отметить несколько моментов. Во-первых, у инструмента есть переключатель «абсолютное/относительное» — если вы хотите выяснить разницу между базовым показателем конверсии в 5% и переменным показателем конверсии в 6%, он составит 1% в абсолютном выражении (6-5=1) или 20% в относительном выражении (6/5=1,2). Во-вторых, внизу страницы есть два «бегунка». Нижний отвечает за требуемый уровень значимости – если вашей целью является получение значимости в 95%, то бегунок нужно выставить на 5%. Верхний бегунок показывает вероятность того, что количество требуемых посещений страницы окажется достаточным – к примеру, если вы хотите узнать количество визитов, необходимых для достижения восьмидесяти процентного шанса обнаружить значимость в 95%, выставьте верхний бегунок на 80%, а нижний на 5%.

6. Чего не нужно делать

Есть несколько простых путей выявить непригодность сплит-теста, которые, однако, далеко не всегда очевидны с первого взгляда:

А) Сплит-тестирование недвоичных порядковых значений

Например, ваша цель – выяснить, имеет ли место значимая разница вероятностей того, что посетители из групп «первоначальная» и «после изменений» купят определенные продукты. Вы помечаете три продукта «1», «2» и «3», а затем вводите эти значения в поля теста на значимость. К сожалению, этот подход не сработает – продукт 2 не является средним значением продуктов 1 и 3.

Б) Настройки распределения трафика

В начале теста вы решаете не рисковать и выставляете распределение трафика 90/10. Спустя какое-то время вы видите, что изменение не привело к заметным изменениям в конверсии, и перемещаете бегунок к значению 50/50. Но возвращающиеся посетители по-прежнему принадлежат к своей первоначальной группе, поэтому вы оказываетесь в ситуации, где версия «до изменений» отличается большей долей вернувшихся посетителей, показывающих высокую вероятность конверсии. Все очень быстро усложняется, и единственный простой путь получить данные, на которые можно положиться, заключается в том, чтобы по отдельности рассматривать новых и вернувшихся посетителей. Однако в этом случае на получение значимых результатов уйдет больше времени. И даже если обе подгруппы покажут значимые результаты, что, если одна из них на самом деле генерирует больше вернувшихся посетителей? В общем, не нужно этого делать и менять в течение теста распределение трафика.

В) Планирование

Выглядит очевидным, но не стоит сравнивать данные, собранные в одно и то же время дня, с данными, собранными в течение суток или в другое время дня. Если вы хотите провести тест в отношении конкретного времени дня, у вас есть два варианта.

1. Обрабатывать запросы посетителей, как и всегда, в течение дня, но показывать им оригинальную версию страницы в то время дня, в котором вы не заинтересованы.

2. Сравнивать яблоки с яблоками – если вы рассматриваете только данные по изменениям за первую половину дня, сравнивайте их с первоначальными данными за первую половину дня.

Надеюсь, что-то из вышеизложенного окажется полезным для оптимизации вашей конверсии . Если у вас есть свои ноу-хау, пожалуйста, излагайте их в комментариях.

Статистическая значимость или р-уровень значимости - основной результат проверки

статистической гипотезы. Говоря техническим языком, это вероятность получения данного

результата выборочного исследования при условии, что на самом деле для генеральной

совокупности верна нулевая статистическая гипотеза - то есть связи нет. Иначе говоря, это

вероятность того, что обнаруженная связь носит случайный характер, а не является свойством

совокупности. Именно статистическая значимость, р-уровень значимости является

количественной оценкой надежности связи: чем меньше эта вероятность, тем надежнее связь.

Предположим, при сравнении двух выборочных средних было получено значение уровня

статистической значимости р=0,05. Это значит, что проверка статистической гипотезы о

равенстве средних в генеральной совокупности показала, что если она верна, то вероятность

случайного появления обнаруженных различий составляет не более 5%. Иначе говоря, если бы

две выборки многократно извлекались из одной и той же генеральной совокупности, то в 1 из

20 случаев обнаруживалось бы такое же или большее различие между средними этих выборок.

То есть существует 5%-ная вероятность того, что обнаруженные различия носят случайный

характер, а не являются свойством совокупности.

В отношении научной гипотезы уровень статистической значимости – это количественный

показатель степени недоверия к выводу о наличии связи, вычисленный по результатам

выборочной, эмпирической проверки этой гипотезы. Чем меньше значение р-уровня, тем выше

статистическая значимость результата исследования, подтверждающего научную гипотезу.

Полезно знать, что влияет на уровень значимости. Уровень значимости при прочих равных

условиях выше (значение р-уровня меньше), если:

Величина связи (различия) больше;

Изменчивость признака (признаков) меньше;

Объем выборки (выборок) больше.

Односторонние еpи двусторонние критерии проверки значимости

Если цель исследования том, чтобы выявить различие параметров двух генеральных

совокупностей, которые соответствуют различным ее естественным условиям (условия жизни,

возраст испытуемых и т. п.), то часто неизвестно, какой из этих параметров будет больше, а

какой меньше.

Например, если интересуются вариативностью результатов в контрольной и

экспериментальной группах, то, как правило, нет уверенности в знаке различия дисперсий или

стандартных отклонений результатов, по которым оценивается вариативность. В этом случае

нулевая гипотеза состоит в том, что дисперсии равны между собой, а цель исследования -

доказать обратное, т.е. наличие различия между дисперсиями. При этом допускается, что

различие может быть любого знака. Такие гипотезы называются двусторонними.

Но иногда задача состоит в том, чтобы доказать увеличение или уменьшение параметра;

например, средний результат в экспериментальной группе выше, чем контрольной. При этом

уже не допускается, что различие может быть другого знака. Такие гипотезы называются

Односторонними.

Критерии значимости, служащие для проверки двусторонних гипотез, называются

Двусторонними, а для односторонних - односторонними.

Возникает вопрос о том, какой из критериев следует выбирать в том или ином случае. Ответ

На этот вопрос находится за пределами формальных статистических методов и полностью

Зависит от целей исследования. Ни в коем случае нельзя выбирать тот или иной критерий после

Проведения эксперимента на основе анализа экспериментальных данных, поскольку это может

Привести к неверным выводам. Если до проведения эксперимента допускается, что различие

Сравниваемых параметров может быть как положительным, так и отрицательным, то следует

В любой научно-практической ситуации эксперимента (обследования) исследователи могут исследовать не всех людей (генеральную совокупность, популяцию), а только определенную выборку. Например, даже если мы исследуем относительно небольшую группу людей, например страдающих определенной болезнью, то и в этом случае весьма маловероятно, что у нас имеются соответствующие ресурсы или необходимость тестировать каждого больного. Вместо этого обычно тестируют выборку из популяции, поскольку это удобнее и занимает меньше времени. В таком случае, откуда нам известно, что результаты, полученные на выборке, представляют всю группу? Или, если использовать профессиональную терминологию, можем ли мы быть уверены, что наше исследование правильно описывает всю популяцию , выборку из которой мы использовали?

Чтобы ответить на этот вопрос, необходимо определить статистическую значимость результатов тестирования. Статистическая значимость {Significant level , сокращенно Sig.), или /7-уровень значимости (p-level) - это вероятность того, что данный результат правильно представляет популяцию, выборка из которой исследовалась. Отметим, что это только вероятность - невозможно с абсолютной гарантией утверждать, что данное исследование правильно описывает всю популяцию. В лучшем случае по уровню значимости можно лишь заключить, что это весьма вероятно. Таким образом, неизбежно встает следующий вопрос: каким должен быть уровень значимости, чтобы можно было считать данный результат правильной характеристикой популяции?

Например, при каком значении вероятности вы готовы сказать, что таких шансов достаточно, чтобы рискнуть? Если шансы будут 10 из 100 или 50 из 100? А что если эта вероятность выше? Что можно сказать о таких шансах, как 90 из 100, 95 из 100 или 98 из 100? Для ситуации, связанной с риском, этот выбор довольно проблематичен, ибо зависит от личностных особенностей человека.

В психологии же традиционно считается, что 95 или более шансов из 100 означают, что вероятность правильности результатов достаточна высока для того, чтобы их можно было распространить на всю популяцию. Эта цифра установлена в процессе научно-практической деятельности - нет никакого закона, согласно которому следует выбрать в качестве ориентира именно ее (и действительно, в других науках иногда выбирают другие значения уровня значимости).

В психологии оперируют этой вероятностью несколько необычным образом. Вместо вероятности того, что выборка представляет популяцию, указывается вероятность того, что выборка не представляет популяцию. Иначе говоря, это вероятность того, что обнаруженная связь или различия носят случайный характер и не являются свойством совокупности. Таким образом, вместо того чтобы утверждать, что результаты исследования правильны с вероятностью 95 из 100, психологи говорят, что имеется 5 шансов из 100, что результаты неправильны (точно так же 40 шансов из 100 в пользу правильности результатов означают 60 шансов из 100 в пользу их неправильности). Значение вероятности иногда выражают в процентах, но чаще его записывают в виде десятичной дроби. Например, 10 шансов из 100 представляют в виде десятичной дроби 0,1; 5 из 100 записывается как 0,05; 1 из 100 - 0,01. При такой форме записи граничным значением является 0,05. Чтобы результат считался правильным, его уровень значимости должен быть ниже этого числа (вы помните, что это вероятность того, что результат неправильно описывает популяцию). Чтобы покончить с терминологией, добавим, что «вероятность неправильности результата» (которую правильнее называть уровнем значимости) обычно обозначается латинской буквой р. В описание результатов эксперимента обычно включают резюмирующий вывод, такой как «результаты оказались значимыми на уровне достоверности (р (р) менее 0,05 (т.е. меньше 5%).

Таким образом, уровень значимости (р ) указывает на вероятность того, что результаты не представляют популяцию. По традиции в психологии считается, что результаты достоверно отражают общую картину, если значение р меньше 0,05 (т.е. 5%). Тем не менее это лишь вероятностное утверждение, а вовсе не безусловная гарантия. В некоторых случаях этот вывод может оказаться неправильным. На самом деле, мы можем подсчитать, как часто это может случиться, если посмотрим на величину уровня значимости. При уровне значимости 0,05 в 5 из 100 случаев результаты, вероятно, неверны. 11а первый взгляд кажется, что это не слишком часто, однако если задуматься, то 5 шансов из 100 - это то же самое, что 1 из 20. Иначе говоря, в одном из каждых 20 случаев результат окажется неверным. Такие шансы кажутся не особенно благоприятными, и исследователи должны остерегаться совершения ошибки первого рода. Так называют ошибку, которая возникает, когда исследователи считают, что обнаружили реальные результаты, а на самом деле их нет. Противоположные ошибки, состоящие в том, что исследователи считают, будто они не обнаружили результата, а на самом деле он есть, называют ошибками второго рода.

Эти ошибки возникают потому, что нельзя исключить возможность неправильности проведенного статистического анализа. Вероятность ошибки зависит от уровня статистической значимости результатов. Мы уже отмечали, что, для того чтобы результат считался правильным, уровень значимости должен быть ниже 0,05. Разумеется, некоторые результаты имеют более низкий уровень, и нередко можно встретить результаты с такими низкими /?, как 0,001 (значение 0,001 говорит о том, что результаты могут быть неправильными с вероятностью 1 из 1000). Чем меньше значение р, тем тверже наша уверенность в правильности результатов .

В табл. 7.2 приведена традиционная интерпретация уровней значимости о возможности статистического вывода и обосновании решения о наличии связи (различий).

Таблица 7.2

Традиционная интерпретация уровней значимости, используемых в психологии

На основе опыта практических исследований рекомендуется: чтобы по возможности избежать ошибок первого и второго рода, при ответственных выводах следует принимать решения о наличии различий (связи), ориентируясь на уровень р п признака.

Статистический критерий (Statistical Test) - это инструмент определения уровня статистической значимости. Это решающее правило, обеспечивающее принятие истинной и отклонение ложной гипотезы с высокой вероятностью .

Статистические критерии обозначают также метод расчета определенного числа и само это число. Все критерии используются с одной главной целью: определить уровень значимости анализируемых с их помощью данных (т.е. вероятность того, что эти данные отражают истинный эффект, правильно представляющий популяцию, из которой сформирована выборка).

Некоторые критерии можно использовать только для нормально распределенных данных (и если признак измерен по интервальной шкале) - эти критерии обычно называют параметрическими. С помощью других критериев можно анализировать данные практически с любым законом распределения - их называют непараметрическими.

Параметрические критерии - критерии, включающие в формулу расчета параметры распределения, т.е. средние и дисперсии (^-критерий Стью- дента, F-критерий Фишера и др.).

Непараметрические критерии - критерии, не включающие в формулу расчета параметров распределения и основанные на оперировании частотами или рангами (критерий Q Розенбаума, критерий U Манна - Уитни

Например, когда мы говорим, что достоверность различий определялась по ^-критерию Стьюдента, то имеется в виду, что использовался метод ^-критерия Стьюдента для расчета эмпирического значения, которое затем сравнивается с табличным (критическим) значением.

По соотношению эмпирического (нами вычисленного) и критического значений критерия (табличного) мы можем судить о том, подтверждается или опровергается наша гипотеза. В большинстве случаев для того, чтобы мы признали различия значимыми, необходимо, чтобы эмпирическое значение критерия превышало критическое, хотя есть критерии (например, критерий Манна - Уитни или критерий знаков), в которых мы должны придерживаться противоположного правила.

В некоторых случаях расчетная формула критерия включает в себя количество наблюдений в исследуемой выборке, обозначаемое как п. По специальной таблице мы определяем, какому уровню статистической значимости различий соответствует данная эмпирическая величина. В большинстве случаев одно и то же эмпирическое значение критерия может оказаться значимым или незначимым в зависимости от количества наблюдений в исследуемой выборке (п ) или от так называемого количества степеней свободы , которое обозначается как v (г>) или как df (иногда d).

Зная п или число степеней свободы, мы по специальным таблицам (основные из них приводятся в приложении 5) можем определить критические значения критерия и сопоставить с ними полученное эмпирическое значение. Обычно это записывается так: «при п = 22 критические значения критерия составляют t St = 2,07» или «при v (d ) = 2 критические значения критерия Стьюдента составляют = 4,30» и т.н.

Обычно предпочтение оказывается все же параметрическим критериям, и мы придерживаемся этой позиции. Считается, что они более надежны, и с их помощью можно получить больше информации и провести более глубокий анализ. Что касается сложности математических вычислений, то при использовании компьютерных программ эта сложность исчезает (но появляются некоторые другие, впрочем, вполне преодолимые).

• В настоящем учебнике мы подробно не рассматриваем проблему статистических
• гипотез (нулевой - Я0 и альтернативной - Нj) и принимаемые статистические решения,поскольку студенты-психологи изучают это отдельно по дисциплине «Математическиеметоды в психологии». Кроме того, необходимо отметить, что при оформлении исследовательского отчета (курсовой или дипломной работы, публикации) статистические гипотезыи статистические решения, как правило, не приводятся. Обычно при описании результатовуказывают критерий, приводят необходимые описательные статистики (средние, сигмы,коэффициенты корреляции и т.д.), эмпирические значения критериев, степени свободыи обязательно р-уровень значимости. Затем формулируют содержательный вывод в отношении проверяемой гипотезы с указанием (обычно в виде неравенства) достигнутого илинедостигнутого уровня значимости.

В таблицах результатов статистических расчётов в курсовых, дипломных и магистерских работах по психологии всегда присутствует показатель «р».

Например, в соответствии с задачами исследования были рассчитаны различия уровня осмысленности жизни у мальчиков и девочек подросткового возраста.

	Среднее значение		U-критерий Манна-Уитни	Уровень статистической значимости (p)
	Мальчики (20 чел.)	Девочки (5 чел.)
Цели	28,9	35,2	17,5	0,027*
Процесс	30,1	32,0	38,5	0,435
Результат	25,2	29,0	29,5	0,164
Локус контроля - «Я»	20,3	23,6		0,067
Локус контроля - «Жизнь»	30,4	33,8	27,5	0,126
Осмысленность жизни	98,9	111,2		0,103

* - различия статистически достоверны (р ≤ 0,05)

В правом столбце указано значение «р» и именно по его величине можно определить значимы различия осмысленности жизни в будущем у мальчиков и девочек или не значимы. Правило простое:

• Если уровень статистической значимости «р» меньше либо равен 0,05, то делаем вывод, что различия значимы. В приведенной таблице различия между мальчиками и девочками значимы в отношении показателя «Цели» - осмысленность жизни в будущем. У девочек этот показатель статистически значимо выше, чем у мальчиков.
• Если уровень статистической значимости «р» больше 0,05, то делается заключение, что различия не значимы. В приведенной таблице различия между мальчиками и девочками не значимы по всем остальным показателям, за исключением первого.

Откуда берется уровень статистической значимости «р»

Уровень статистической значимости вычисляется статистической программой вместе с расчётом статистического критерия. В этих программах можно также задать критическую границу уровня статистической значимости и соответствующие показатели будут выделяться программой.

Например, в программе STATISTICA при расчете корреляций можно установить границу «р», например, 0,05 и все статистически значимые взаимосвязи будут выделены красным цветом.

Если расчёт статистического критерия проводится вручную, то уровень значимости «р» выявляется путем сравнения значения полученного критерия с критическим значением.

Что показывает уровень статистической значимости «р»

Все статистические расчеты носят приблизительный характер. Уровень этой приблизительности и определяет «р». Уровень значимости записывается в виде десятичных дробей, например, 0,023 или 0,965. Если умножить такое число на 100, то получим показатель р в процентах: 2,3% и 96,5%. Эти проценты отражают вероятность ошибочности нашего предположения о взаимосвязи, например, между агрессивностью и тревожностью.

То есть, коэффициент корреляции 0,58 между агрессивностью и тревожностью получен при уровне статистической значимости 0,05 или вероятности ошибки 5%. Что это конкретно означает?

Выявленная нами корреляция означает, что в нашей выборке наблюдается такая закономерность: чем выше агрессивность, тем выше тревожность. То есть, если мы возьмем двух подростков, и у одного тревожность будет выше, чем у другого, то, зная о положительной корреляции, мы можем утверждать, что у этого подростка и агрессивность будет выше. Но так как в статистике все приблизительно, то, утверждая это, мы допускаем, что можем ошибиться, причем вероятность ошибки 5%. То есть, сделав 20 таких сравнений в этой группе подростков, мы можем 1 раз ошибиться с прогнозом об уровне агрессивности, зная тревожность.

Какой уровень статистической значимости лучше: 0,01 или 0,05

Уровень статистической значимости отражает вероятность ошибки. Следовательно, результат при р=0,01 более точный, чем при р=0,05.

В психологических исследованиях приняты два допустимых уровня статистической значимости результатов:

р=0,01 - высокая достоверность результата сравнительного анализа или анализа взаимосвязей;

р=0,05 - достаточная точность.

Надеюсь, эта статья поможет вам написать работу по психологии самостоятельно. Если понадобится помощь, обращайтесь (все виды работ по психологии; статистические расчеты).