Главная / Уход

Сущность теории непараметрической статистики. Случай одинаковых рангов

Использование порядковой шкалы позволяет присваивать ранги объектам по какому-либо признаку. Таким образом, метрические значения переводятся в ранговые. При этом фиксируются различия в степени выраженности свойств. В процессе ранжирования следует придерживаться 2 правил.

Правило порядка ранжирования. Надо решить, кто получает первый ранг: объект с самой большей степенью выраженности какого-либо качества или наоборот. Чаще всего это абсолютно безразлично и не отражается на конечном результате. Традиционно принято первый ранг приписывать объектам с большей степенью выраженности качества (большему значению – меньший ранг). Например, чемпиону присуждают первое место, а не наоборот. Хотя, и здесь если бы был принят обратный порядок, то результаты от этого не изменились бы. Так что порядок ранжирования каждый исследователь вправе определять сам. Например, Е. В. Сидоренко рекомендует меньшему значению приписывать меньший ранг. В некоторых случаях это удобнее, но непривычнее.

Например: имеется неупорядоченная выборка, данные которой необходимо проранжировать. {2, 7, 6, 8, 11, 15, 9}. После упорядочивания выборки ранжируем ее.

Метрические данные	Альтернативный вариант:	Метрические данные

Отдельно следует сказать следующее. Существует группа редко используемых непараметрических критериев (Т-критерий Вилкоксона, U-критерий Манна-Уитни,Q-критерий Розенбаума и др.), при работе с которыми всегда надо меньшему значению приписывать меньший ранг.

Правило связанных рангов. Объектам с одинаковой выраженностью свойств приписывается один и тот же ранг. Этот ранг представляет собой среднее значение тех рангов, которые они получили бы, если бы не были равны. Например, надо проранжировать выборку, содержащую ряд одинаковых метрических данных: {4, 5, 9, 2, 6, 5, 9, 7, 5, 12}. После упорядочивания выборки следует вычислить среднее арифметическое значение связанных рангов.

Метрические данные	Предварительное ранжирование	Окончательное ранжирование

Задания для самостоятельной работы.

Проранжировать выборку по правилу «большему значению – меньший ранг»: {111, 104, 115, 107, 95, 104, 104}.

Проранжировать выборку по правилу «меньшему значению – меньший ранг» {20, 25, 8, 7, 20, 14, 27}.

Объединить две предыдущие выборки и провести ранжирование по правилу «большему значению – меньший ранг»

Показатели каких признаков из Таблицы Iявляются номинативными, каких – метрическими?

Перевести показатели осведомленности из Таблицы IПриложения в ранговую шкалу. Выделить уровни выраженности показателей посредством их перевода в номинативную шкалу.

Таблица I Данные для обработки

учащиеся

профиль ВУЗа

осведомленность

скрытые фигуры

пропущенные

арифметика

понятливость

исключение

изображений

аналогии

числовые ряды

умозаключения

геометрическое сложение

заучивание слов

средний IQ

экстраверсия-

интроверсия

нейротизм

средняя отметка

Профиль ВУЗа: 0 - выбор учеником гуманитарного профиля;

1 - выбор учеником математического или естественно-научного профиля

При изучении общественного здоровья и здравоохранения в научных и практических целях исследователю часто приходится проводить статистический анализ связей между факторными и результативными признаками статистический совокупности (причинно-следственная связь) или определение зависимости параллельных изменений нескольких признаков этой совокупности от какой либо третьей величины (от общей их причины). Необходимо уметь изучать особенности этой связи, определять ее размеры и направление, а также оценивать ее достоверность. Для этого используются методы корреляции.

Виды проявления количественных связей между признаками
- функциональная связь
- корреляционная связь
Определения функциональной и корреляционной связи
Функциональная связь - такой вид соотношения между двумя признаками, когда каждому значению одного из них соответствует строго определенное значение другого (площадь круга зависит от радиуса круга и т.д.). Функциональная связь характерна для физико-математических процессов.
Корреляционная связь - такая связь, при которой каждому определенному значению одного признака соответствует несколько значений другого взаимосвязанного с ним признака (связь между ростом и массой тела человека; связь между температурой тела и частотой пульса и др.). Корреляционная связь характерна для медико-биологических процессов.
Практическое значение установления корреляционной связи . Выявление причинно-следственной между факторными и результативными признаками (при оценке физического развития, для определения связи между условиями труда, быта и состоянием здоровья, при определении зависимости частоты случаев болезни от возраста, стажа, наличия производственных вредностей и др.)
Зависимость параллельных изменений нескольких признаков от какой-то третьей величины. Например, под воздействием высокой температуры в цехе происходят изменения кровяного давления, вязкости крови, частоты пульса и др.
Величина, характеризующая направление и силу связи между признаками . Коэффициент корреляции, который одним числом дает представление о направлении и силе связи между признаками (явлениями), пределы его колебаний от 0 до ± 1
Способы представления корреляционной связи
- график (диаграмма рассеяния)
- коэффициент корреляции
Направление корреляционной связи
- прямая
- oбратная
Сила корреляционной связи
- сильная: ±0,7 до ±1
- средняя: ±0,3 до ±0,699
- слабая: 0 до ±0,299
Методы определения коэффициента корреляции и формулы
- метод квадратов (метод Пирсона)
- ранговый метод (метод Спирмена)
Методические требования к использованию коэффициента корреляции
- измерение связи возможно только в качественно однородных совокупностях (например, измерение связи между ростом и весом в совокупностях, однородных по полу и возрасту)
- расчет может производиться с использованием абсолютных или производных величин
- для вычисления коэффициента корреляции используются не сгруппированные вариационные ряды (это требование применяется только при вычислении коэффициента корреляции по методу квадратов)
- число наблюдений не менее 30
Рекомендации по применению метода ранговой корреляции (метод Спирмена)
- когда нет необходимости в точном установлении силы связи, а достаточно ориентировочных данных
- когда признаки представлены не только количественными, но и атрибутивными значениями
- когда ряды распределения признаков имеют открытые варианты (например, стаж работы до 1 года и др.)
Рекомендации к применению метода квадратов (метод Пирсона)
- когда требуется точное установление силы связи между признаками
- когда признаки имеют только количественное выражение
Методика и порядок вычисления коэффициента корреляции
1) Метод квадратов
2) Ранговый метод
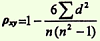
Схема оценки корреляционной связи по коэффициенту корреляции
Вычисление ошибки коэффициента корреляции
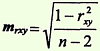
Оценка достоверности коэффициента корреляции,полученного методом ранговой корреляции и методом квадратов
Способ 1
Достоверность определяется по формуле:
Критерий t оценивается по таблице значений t с учетом числа степеней свободы (n - 2), где n - число парных вариант. Критерий t должен быть равен или больше табличного, соответствующего вероятности р ≥99%.
Способ 2
Достоверность оценивается по специальной таблице стандартных коэффициентов корреляции. При этом достоверным считается такой коэффициент корреляции, когда при определенном числе степеней свободы (n - 2), он равен или более табличного, соответствующего степени безошибочного прогноза р ≥95%.

на применение метода квадратов

Задание: вычислить коэффициент корреляции, определить направление и силу связи между количеством кальция в воде и жесткостью воды, если известны следующие данные (табл. 1). Оценить достоверность связи. Сделать вывод.

Таблица 1

Обоснование выбора метода. Для решения задачи выбран метод квадратов (Пирсона), т.к. каждый из признаков (жесткость воды и количество кальция) имеет числовое выражение; нет открытых вариант.

Решение .
Последовательность расчетов изложена в тексте, результаты представлены в таблице. Построив ряды из парных сопоставляемых признаков, обозначить их через х (жесткость воды в градусах) и через у (количество кальция в воде в мг/л).

Жесткость воды (в градусах)	Количество кальция в воде (в мг/л)	d х	d у	d х х d у	d x 2	d y 2
4 8 11 27 34 37	28 56 77 191 241 262	-16 -12 -9 +7 +14 +16	-114 -86 -66 +48 +98 +120	1824 1032 594 336 1372 1920	256 144 81 49 196 256	12996 7396 4356 2304 9604 14400
М х =Σ х / n	М у =Σ у / n			Σ d х x d у =7078	Σ d х 2 =982	Σ d y 2 =51056
М х =120/6=20	М y =852/6=142

Определить средние величины M x ряду вариант "х" и М у в ряду вариант "у" по формулам:
М х = Σх/n (графа 1) и
М у = Σу/n (графа 2)
Найти отклонение (d х и d у) каждой варианты от величины вычисленной средней в ряду "x" и в ряду "у"
d х = х - М х (графа 3) и d y = у - М у (графа4).
Найти произведение отклонений d x х d y и суммировать их: Σ d х х d у (графа 5)
Каждое отклонение d x и d у возвести в квадрат и суммировать их значения по ряду "х" и по ряду "у": Σ d x 2 = 982 (графа 6) и Σ d y 2 = 51056 (графа 7).
Определить произведение Σ d x 2 х Σ d y 2 и из этого произведения извлечь квадратный корень
Полученные величины Σ (d x x d y) и √(Σd x 2 x Σd y 2) подставляем в формулу расчета коэффициента корреляции:

Определить достоверность коэффициента корреляции:
1-й способ. Найти ошибку коэффициента корреляции (mr xy) и критерий t по формулам:

Критерий t = 14,1, что соответствует вероятности безошибочного прогноза р > 99,9%.

2-й способ. Достоверность коэффициента корреляции оценивается по таблице "Стандартные коэффициенты корреляции" (см. приложение 1). При числе степеней свободы (n - 2)=6 - 2=4, наш расчетный коэффициент корреляции r xу = + 0,99 больше табличного (r табл = + 0,917 при р = 99%).

Вывод. Чем больше кальция в воде, тем она более жесткая (связь прямая, сильная и достоверная : r ху = + 0,99, р > 99,9%).

на применение рангового метода

Задание: методом рангов установить направление и силу связи между стажем работы в годах и частотой травм, если получены следующие данные:

Обоснование выбора метода: для решения задачи может быть выбран только метод ранговой корреляции, т.к. первый ряд признака "стаж работы в годах" имеет открытые варианты (стаж работы до 1 года и 7 и более лет), что не позволяет использовать для установления связи между сопоставляемыми признаками более точный метод - метод квадратов.

Решение . Последовательность расчетов изложена в тексте, результаты представлены в табл. 2.

Таблица 2

Стаж работы в годах	Число травм	Порядковые номера (ранги)		Разность рангов	Квадрат разности рангов
Стаж работы в годах	Число травм	X	Y	d(х-у)	d 2
До 1 года	24	1	5	-4	16
1-2	16	2	4	-2	4
3-4	12	3	2,5	+0,5	0,25
5-6	12	4	2,5	+1,5	2,25
7 и более	6	5	1	+4	16
					Σ d 2 = 38,5

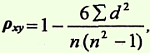
Стандартные коэффициенты корреляции, которые считаются достоверными (по Л.С. Каминскому)

Число степеней свободы - 2	Уровень вероятности р (%)
Число степеней свободы - 2	95%	98%	99%
1	0,997	0,999	0,999
2	0,950	0,980	0,990
3	0,878	0,934	0,959
4	0,811	0,882	0,917
5	0,754	0,833	0,874
6	0,707	0,789	0,834
7	0,666	0,750	0,798
8	0,632	0,716	0,765
9	0,602	0,885	0,735
10	0,576	0,858	0,708
11	0,553	0,634	0,684
12	0,532	0,612	0,661
13	0,514	0,592	0,641
14	0,497	0,574	0,623
15	0,482	0,558	0,606
16	0,468	0,542	0,590
17	0,456	0,528	0,575
18	0,444	0,516	0,561
19	0,433	0,503	0,549
20	0,423	0,492	0,537
25	0,381	0,445	0,487
30	0,349	0,409	0,449

Власов В.В. Эпидемиология. - М.: ГЭОТАР-МЕД, 2004. - 464 с.
Лисицын Ю.П. Общественное здоровье и здравоохранение. Учебник для вузов. - М.: ГЭОТАР-МЕД, 2007. - 512 с.
Медик В.А., Юрьев В.К. Курс лекций по общественному здоровью и здравоохранению: Часть 1. Общественное здоровье. - М.: Медицина, 2003. - 368 с.
Миняев В.А., Вишняков Н.И. и др. Социальная медицина и организация здравоохранения (Руководство в 2 томах). - СПб, 1998. -528 с.
Кучеренко В.З., Агарков Н.М. и др.Социальная гигиена и организация здравоохранения (Учебное пособие) - Москва, 2000. - 432 с.
С. Гланц. Медико-биологическая статистика. Пер с англ. - М., Практика, 1998. - 459 с.

В анализе социально-экономических явлений часто приходится прибегать к различным условным оценкам с помощью рангов, а взаимосвязь между отдельными признаками измерять с помощью непараметрических коэффициентов связи.

Ранжирование - это процедура упорядочения объектов изучения, которая выполняется на основе предпочтения.

Ранг - это порядковый номер значений признака, расположенных в порядке возрастания или убывания их величин. Если значения признака имеют одинаковую количественную оценку, то ранг всех этих значений принимается равным средней арифметической из соответствующих номеров мест, которые они определяют. Данные ранги называются связными.

Среди непараметрических методов оценки тесноты связи наибольшее значение имеют ранговые коэффициенты корреляции Спирмена (р1?/) и Кендалла (т^). Эти коэффициенты могут быть использованы для определения тесноты связи между как количественными, так и качественными признаками.

Коэффициент корреляции рангов (коэффициент Спирмена) рассчитывают по формуле

где (11 - квадраты разности рангов; п - число наблюдений (число пар рангов).

Коэффициент Спирмена принимает любые значения в интервале [-1; 1].

Пример. 11о данным о покупке и продаже гражданами субъектов Приволжского федерального округа РФ валюты через кредитные организации в 2010 г. определим зависимость между этими признаками с помощью коэффициента Спирмена (табл. 7.14).

Таблица 7.14. Расчет коэффициента Спирмена

Субъект	Покупка валюты х, млн руб.	Продажа валюты у, млн руб.	Ранг		поп а рангов	Квадрат разности рангов $
Субъект	Покупка валюты х, млн руб.	Продажа валюты у, млн руб.	К	Ry	поп а рангов	Квадрат разности рангов $
1. Республика Башкортостан
2. Республика Марий Эл
3. Республика Мордовия
4. Республика Татарстан
5. Удмуртская Республика
6. Чувашская Республики
7. Пермский край
8. Кировская область
9. Нижегородская область
10. Оренбургская область
11. Пензенская область
12. Самарская область
13. Саратовская область
14. Ульяновская область

Рассчитаем коэффициент корреляции рангов Спирмена:

В результате расчета мы определили, что связь между покупкой и продажей валюты гражданами субъектов Приволжского федерального округа РФ через кредитные организации в 2010 г. сильная, близкая к функциональной.

Ранговый коэффициент корреляции Кендалла также используют для измерения степени тесноты и направления связи между качественными и количественными признаками, характеризующими однородные объекты и ранжированными по одному принципу. Расчет рангового коэффициента Кендалла осуществляют но формуле

где 5 - сумма разностей между числом последовательностей и числом инверсий по второму признаку; п - число наблюдений.

Расчет данного коэффициента выполняется в такой последовательности.

1. Значения х ранжируются в порядке возрастания или убывания.
2. Значения у располагаются в порядке, соответствующем значениям х.
3. Для каждого ранга у определяется число следующих за ним значений рангов, превышающих его величину. Таким образом, путем сложения чисел определяется величина Р как мера соответствия последовательностей рангов пох и у, которая учитывается со знаком "+".
4. Для каждого ранга у определяется число следующих за ним значений рангов, меньших его величины. Суммарная величина обозначается через (2 и фиксируется со знаком "-".
5. Определяется сумма баллов по всем членам ряда.

Связь между признаками признается статистически значимой, если коэффициенты ранговой корреляции Спирмена и Кендалла больше 0,5.

По данным табл. 7.14 получены результаты, представленные в табл. 7.15.

Таким образом, ранговый коэффициент корреляции Кендалла составит

Таблица 7.15.

что также свидетельствует о сильной связи между покупкой и продажей валюты гражданами субъектов Приволжского федерального округа РФ через кредитные организации в 2009 г.

Множественный коэффициент ранговой корреляции (коэффициент конкордации) применяют для определения тесноты связи между произвольным числом ранжированных признаков. Его вычисляют по формуле

где 5 - отклонение суммы квадратов рангов от средней квадратов рангов; т - количество факторов; п - число наблюдений.

Пример. Определим степень тесноты связи между такими основными показателями торговли технологиями со странами СНГ в 2010 г., как число экспортных соглашений, стоимость предмета соглашения и поступление средств (табл. 7.16).

Таблица 7.16. Расчет коэффициента конкордации

Страна	Число соглашений X	Стоимость предмета соглашения у, млн долл.	Поступление средств за год г, млн долл.	К	Сумма строк	Квадрат суммы
1. Азербайджан
2. Армения
3. Беларусь
4. Казахстан
5. Киргизия
6. Республика Молдова

При выставлении экспертных оценок или в других случаях ранжирования возникают ситуации, когда двум или большему числу качеств приписываются одинаковые ранги. В этом случае правила ранжирования таковы:

1. Наименьшему числовому значению приписывается ранг 1.

2. Наибольшему числовому значению приписывается ранг, равный количеству ранжируемых величин.

3. В случае если несколько исходных числовых значений оказались равными, то им приписывается ранг, равный средней величине тех рангов, которые эти величины получили бы, если бы они стояли по порядку друг за другом и не были бы равны.

Отметим, что под этот случай могут попасть как первые, так и последние величины исходного ряда для ранжирования.

4. Общая сумма реальных рангов должна совпадать с расчетной, определяемой по формуле (1).

Например, психолог получил у 11 испытуемых следующие значения показателя невербального интеллекта: 113, 107, 123, 122, 117, 117, 105, 108, 114, 102, 104. Необходимо проранжировать эти показатели.

№ испытуемых п/п	Показатели интеллекта	Условные ранги	Ранги




		(8)	8,5
		(9)	8,5

Т.к. у 5 и 6 испытуемых показатели интеллекта равные, то им необходимо поставить условные ранги, обязательно идущие по порядку друг за другом – и отметить эти ранги круглыми скобками – (). Но так как они должны иметь одинаковые ранги. То в столбец ранги мы должны поместить среднее арифметическое рангов, проставленных в скобках, т.е. . Часто условные и реальные ранги записывают в одном столбце

Проверим правильность ранжирования по формуле (1):

Просуммируем реальные ранги: 6+4+11+10+8,5+8,5+3+5+7+1+2=66.

Т.к. суммы совпали, то ранжирование выполнено верно.

В ранговой шкале применяется множество статистических методов. Наиболее часто к измерениям, полученным в этой шкале применяются коэффициенты корреляции Спирмена и Кэндалла, кроме того, применительно к данным, полученным в этой шкале, используют разнообразные критерии различий.

Шкала интервалов

В шкале интервалов каждое из возможных значений измеренных величин отстоит от ближайшего на равном расстоянии. Главное понятие этой шкалы - интервал , который можно определить как долю или часть измеряемого свойства между двумя соседними позициями на шкале.

Размер интервала - величина фиксированная и постоянная на всех участках шкалы. Для измерения посредством шкалы интервалов устанавливаются специальные единицы измерения, в психологии это стены . При работе с этой шкалой измеряемому свойству или предмету присваивается число, равное количеству единиц измерения, эквивалентное количеству имеющегося свойства. Важной особенностью шкалы интервалов является то, что у нее нет естественной точки отсчета (нуль условен и не указывает на отсутствие измеряемого свойства).

Так, в психологии часто используется семантический дифференциал Ч.Осгуда, который является примером измерения по интервальной шкале различных психологических особенностей личности, социальных установок, ценностных ориентации, субъективно-личностного смысла, различных аспектов самооценки.

3 - 2 - 1 0 +1 +2 +3

Абсолютно Не знаю Совершенно

не согласен (не уверен) согласен

Однако, как подчеркивают С. Стивенс и ряд других исследователей, психологические измерения в шкале интервалов по сущности нередко оказываются измерениями, выполненными в шкале порядков. Основанием для этого утверждения служит тот факт, что функциональные возможности человека меняются в зависимости от разных условий. При измерении, например, силы с помощью динамометра или устойчивости внимания с помощью секундомера, результаты измерения в начале и в конце опыта по причине усталости испытуемого не будут квантифицироваться равными интервалами.

Только измерение по строго стандартизированной тестовой методике, при условии того, что распределение значений в репрезентативной (см. ниже) выборке достаточно близко к нормальному (см. ниже), может считаться измерением в интервальной шкале. Примером последнего могут служить стандартизованные тесты интеллекта, где условная единица измерения IQ эквивалентна как при низких, так и при высоких значениях интеллекта

Принципиально важным является и то, что к экспериментальным данным, полученным в этой шкале, применимо достаточно большое число статистических методов.

Шкала отношений

Шкалу отношений называют также шкалой равных отношений. Особенностью этой шкалы является наличие твердо фиксированного нуля, который означает полное отсутствие какого-либо свойства или признака. Шакала отношений является наиболее информативной шкалой, допускающей любые математические операции и использование разнообразных статистических методов.

Шкала отношений по сути очень близка интервальной, поскольку если строго фиксировать начало отсчета, то любая интервальная шкала превращается в шкалу отношений.

Именно в шкале отношений производятся точные и сверхточные измерения в таких науках, как физика, химия, микробиология. Измерение по шкале отношений производятся и в близких к психологии науках, таких, как психофизика, психофизиология, психогенетика.

Коэффициент тесноты связи между признаками, рассмотренный в предыдущем разделе, можно применять, если изучаемые признаки являются количественными. При этом используется вычисление основных параметров распределения (средних величин, дисперсий), т.е. параметрический метод.

В статистической практике изучения общественно-экономических явлений и процессов приходится сталкиваться с задачами измерения связи между качественными признаками, к которым параметрические методы анализа в их обычном виде неприменимы. В этом случае используют так называемые непараметрические методы.

В анализе социально-экономических явлений широко используются ранговые коэффициенты корреляции (коэффициенты корреляции рангов), когда коррелируют не непосредственные значения х и у, а их ранги, т.е. номера их мест, занимаемых в каждом ряду значений по возрастанию или убыванию. К таким непараметрическим коэффициентам относятся коэффициенты рангов Спирмена и Кендалла.

Если п вариантов ряда расположены в соответствии с возрастанием или убыванием признака х, то говорят, что объекты ранжированы по этому признаку. Ранг для х,- указывает место, которое занимает i-e значение признака среди других п значений признака х (/ = 1,2,___, п).

Например, при исследовании рынка можно задаться целью выяснения предпочтений потребителей при выборе товара (при покупке акций, мороженого, автомобиля и т.п.) таким образом, чтобы они распределили товар в порядке возрастания (или убывания) своих потребительских предпочтений. Если имеется два набора ранжированных данных, то можно установить степень линейной зависимости между ними.

Пример 6.7. Предположим, имеется 5 продуктов (табл. 6.7), которые ранжированы по порядку предпочтений от 1 до 5 в соответствии с двумя характеристиками Aw В.

Исходные ранжировки

Таблица 6 .7

Необходимо исследовать тесноту статистической связи между характеристиками.

Решение. Использование для определения интенсивности связи между признаками коэффициента Пирсона будет неверным, так как этот коэффициент применяется для признаков, измеряемых количественно. Так, например, при определении взаимосвязи между ростом и весом мы измеряем рост в сантиметрах, а вес в килограммах, при этом есть возможность точно определить на шкале измерений разность значений этих признаков для любого человека (иначе - расстояние между ними на шкале измерений). Возьмем признак, измеренный в ранговой шкале, - экзаменационная оценка. Значит ли, что у получившего двойку студента знаний в два раза меньше, чем у того, кто получил четверку? Или двое студентов, получивших тройки, имеют абсолютно одинаковый уровень знаний? Ответ - нет, преподаватель упорядочивает их уровень знаний в определенной последовательности, в соответствии с критериями оценки знаний по конкретному предмету, но расстояние между значениями признаков на такой шкале не является строго фиксированным.

Для определения наличия взаимосвязи между ранговыми оценками используется коэффициент ранговой корреляции Спирмена. Его расчет основан на различиях между рангами.

Обозначим разность рангов d = ранг А ~ ранг В.

Коэффициент Спирмена

где п - число пар ранжированных наблюдений.

В примере имеем пять пар рангов, следовательно, п- 5. Сумма ct равна

Тогда коэффициент Спирмена

Коэффициент Спирмена изменяется в интервале [-1; 1] и интерпретируется так же, как и коэффициент Пирсона. Отличие в том, что он вычисляется для ранжированных данных.

Значение 0,6 позволяет сделать вывод о заметной линейной связи между двумя характеристиками товаров.

Значимость коэффициента Спирмена проверяется на основе t критерия Стьюдента по формуле

Значение коэффициента считается существенным, если t paсч > > 6фит;а (и - 2) для заданного уровня значимости а.

Коэффициент корреляции рангов (при условии, что ранги не повторяются) может быть рассчитан и по формуле, предложенной английским статистиком М. Кендаллом:

где S - фактическая разность рангов; ~ п (п - l) - максимальная сумма рангов.

Этот коэффициент изменяется в интервале от [-1; 1] и интерпретируется так же, как и коэффициент Пирсона, но дает более строгую

оценку связи, чем коэффициент Спирмена, причем р = - т. Это соотношение выполняется при большом числе наблюдений (п > 30), и слабых либо умеренно тесных связях.

При расчете коэффициента Кендалла соблюдается следующая последовательность действий:

1. Значения х ранжируются в порядке возрастания.
2. Значения у располагаются в порядке, соответствующем значениям х.
3. Для каждого ранга у определяется число следующих за ним значений рангов, превышающих его величину. Результат записывается в столбец «+».
4. Для каждого ранга у определяется число следующих за ним меньших значений рангов. Результат записывается в столбец «-».
5. Находится сумма в столбце «+» и обозначается Р, в столбце «-» и обозначается Q. Определяется S = P- Q.

Значимость коэффициента корреляции рангов Кендалла проверяется по формуле

где щ_ а/2 (п - 2) - квантиль, определяемый по таблице нормального распределения для выбранного уровня значимости а и заданного п.

Пример 6.8. Рассчитаем коэффициент Кендалла на основании данных примера 6.7.

Решение. Проведем необходимые расчеты в табл. 6.8.

Действительно, если полученное значение т умножить на 1,5, то получим 0,6 - значение коэффициента Спирмена, рассчитанное в примере 6.7.

Расчетная таблица

Рассмотрим корреляцию альтернативных признаков, т.е.признаков, принимающих только два возможных значения. Исследования их корреляции основано на показателях, построенных на четырехклеточных таблицах, в которые сводится число единиц для заданных значений признаков:

Решение. Для измерения тесноты взаимосвязи признаков производится расчет коэффициента контингенции по формуле

Коэффициент контингенции принимает значения на интервале [-1; 1 ]. Интерпретация аналогична коэффициенту корреляции. Мы получили слабую отрицательную связь.

Другой метод измерения связи основан на расчете коэффициента ассоциации:

„ л 30x5-20x15 л „

Получим: Q =-= -0,33

Знак «минус» перед коэффициентом указывает на то, что чем больше студентов было привито от гриппа, тем ниже заболеваемость.

Коэффициент контингенции всегда бывает меньше коэффициента ассоциации и дает более корректную оценку тесноты связи.

Для оценки тесноты связи между признаками, принимающими любое число вариантов значений (категориальные, номинальные признаки), применяется коэффициент взаимной сопряженности Пирсона. Основой изучения связи между категориальными признаками служит таблица сопряженности - двумерное распределение единиц совокупности по признакам. Вся информация о наличии или отсутствии связи содержится в совместных частотах сочетаний признаков.

Информация для оценки этой связи группируется в виде таблицы (например, для трех значений первого признака и двух - второго), табл. 6.10.

Таблица 6.10

Пример таблицы сопряженности

Признак		Итого


	Ъгпц	ЪЪгпц

Обозначения: ту - частоты взаимного сочетания двух атрибутивных признаков; п = YLmy - число наблюдений.

Коэффициент взаимной сопряженности Пирсона определяется по формуле

где ср - показатель средней квадратической сопряженности:

Коэффициент взаимной сопряженности принимает значения в интервале и интерпретируется подобно коэффициенту парной линейной корреляции Пирсона.

Пример 6.10. Для изучения влияния условий труда на взаимоотношения в коллективе было проведено выборочное обследование 250 работников предприятия, ответы которых распределились, как представлено в табл. 6.11.

Таблица 6.11

Исходные данные об условиях труда и взаимоотношениях в коллективе

Требуется охарактеризовать связь между исследуемыми показателями с помощью коэффициента взаимной сопряженности Пирсона.

Решение.

Полученное значение коэффициента сопряженности свидетельствует, что связь между условиями труда и взаимоотношениями в коллективе умеренная.