Условимся считать, что под «действиями с дробями» на нашем уроке будут пониматьсядействия с обыкновенными дробями. Обыкновенная дробь — это дробь, обладающая такими атрибутами, какчислитель, дробная черта и знаменатель. Это отличает обыкновенную дробь от десятичной, которая получаетсяиз обыкновенной путём приведения знаменателя к числу, кратному 10. Десятичная дробь записывается с запятой,отделяющей целую часть от дробной. У нас пойдёт речь о действиях с обыкновенными дробями, так как именноони вызывают наибольшие затруднения у студентов, позабывших основы этой темы, пройденной в первой половинешкольного курса математики. Вместе с тем при преобразованиях выражений в высшей математике используютсяв основном именно действия с обыкновенными дробями. Одни сокращения дробей чего стоят! Десятичные же дробиособых затруднений не вызывают. Итак, вперёд!
Две дробииназываются равными, если .
Например, ,так как
Равными также являются дробии (так как), и (так как).
Очевидно, равными являются и дробии . Это означает,что если числитель и знаменатель данной дроби умножить или разделить на одно и то же натуральное число,то получится дробь, равная данной: .
Это свойство называется основным свойством дроби.
Основное свойство дроби можно использовать для перемены знаков у числителя и знаменателядроби. Если числитель и знаменатель дробиумножить на -1, то получим .Это означает, что значение дроби не изменится, если одновременно изменить знаки у числителя и знаменателя.Если же изменить знак только у числителя или только у знаменателя, то и дробь изменит свой знак:
Сокращение дробей
Пользуясь основным свойством дроби, можно заменить данную дробь другой дробью,равной данной, но с меньшим числителем и знаменателем. Такую замену называют сокращением дроби.
Пусть, например, дана дробь .Числа 36 и 48 имеют наибольший общий делитель 12. Тогда
![]() .
.
В общем случае сокращение дроби возможно всегда, если числитель и знаменатель неявляются взаимно простыми числами. Если числитель и знаменатель — взаимно простые числа, то дробьназывается несократимой.
Итак, сократить дробь — это значит разделить числитель и знаменатель дроби на общиймножитель. Всё вышесказанное применимо и к дробным выражениям, содержащим переменные.
Пример 1. Сократить дробь
Решение. Для разложения числителя на множители, представив предварительно одночлен- 5xy в виде суммы — 2xy — 3xy,получим

Для разложения знаменателя на множители используем формулу разности квадратов:
В результате
![]() .
.
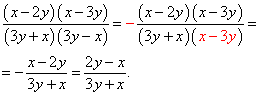
Приведение дробей к общему знаменателю
Пусть даны две дроби и. Они имеют разныезнаменатели: 5 и 7. Пользуясь основным свойством дроби, можно заменить эти дроби другими, равными им,причём такими, что у полученных дробей будут одинаковые знаменатели. Умножив числитель и знаменательдроби на 7, получим
Умножив числитель и знаменатель дробина 5, получим
Итак, дроби приведены к общему знаменателю:
![]() .
.
Но это не единственное решение поставленной задачи: например, данные дроби можнопривести также к общему знаменателю 70:
![]() ,
,
![]()
и вообще к любому знаменателю, делящемуся одновременно на 5 и 7.
Рассмотрим ещё один пример: приведём к общему знаменателю дроби и. Рассуждая, как впредыдущем примере, получим
![]() ,
,
![]() .
.
Но в данном случае можно привести дроби к общему знаменателю, меньшему, чем произведениезнаменателей этих дробей. Найдём наименьшее общее кратное чисел 24 и 30: НОК(24, 30) = 120.
Так как 120:4=5, то чтобы записать дробьсо знаменателем 120, надо и числитель, и знаменатель умножить на 5, это число называется дополнительныммножителем. Значит ![]() .
.
Далее, получаем 120:30=4. Умножив числитель и знаменатель дроби на дополнительныймножитель 4, получим ![]() .
.
Итак, данные дроби приведены к общему знаменателю.
Наименьшее общее кратное знаменателей этих дробей является наименьшим возможнымобщим знаменателем.
Для дробных выражений, в которые входят переменные, общим знаменателем являетсямногочлен, который делится на знаменатель каждой дроби.
Пример 2. Найти общий знаменатель дробей и.
Решение. Общим знаменателем данных дробей является многочлен,так как он делится и на ,и на .Однако этот многочлен не единственный, который может быть общим знаменателем данных дробей.Им может быть также многочлен ![]() ,и многочлен
,и многочлен ![]() , имногочлен
, имногочлен ![]() и т.д.Обычно берут такой общий знаменатель, что любой другой общий знаменатель делится на выбранный безостатка. Такой знаменатель называется наименьшим общим знаменателем.
и т.д.Обычно берут такой общий знаменатель, что любой другой общий знаменатель делится на выбранный безостатка. Такой знаменатель называется наименьшим общим знаменателем.
В нашем примере наименьший общий знаменатель равен .Получили:
![]() ;
;
![]() .
.
Нам удалось привести дроби к наименьшему общему знаменателю. Это произошло путёмумножения числителя и знаменателя первой дроби на ,а числителя и знаменателя второй дроби — на .Многочлены и называютсядополнительными множителями, соответственно для первой и для второй дроби.
Сложение и вычитание дробей
Сложение дробей определяется следующим образом:
![]() .
.
Например,
![]() .
.
Если b = d, то
![]() .
.
Это значит, что для сложения дробей с одинаковым знаменателем достаточно сложитьчислители, а знаменатель оставить прежним. Например,
![]() .
.
Если же складываются дроби с разными знаменателями, то обычно приводят дроби кнаименьшему общему знаменателю, а потом складывают числители. Например,
![]() .
.
Теперь рассмотрим пример сложения дробных выражений с переменными.
Пример 3. Преобразовать в одну дробь выражение
![]() .
.
Решение. Найдём наименьший общий знаменатель. Для этого сначала разложимзнаменатели на множители.
Теперь, когда мы научились складывать и умножать отдельные дроби, можно рассматривать более сложные конструкции. Например, что, если в одной задаче встречается и сложение, и вычитание, и умножение дробей?
В первую очередь, надо перевести все дроби в неправильные. Затем последовательно выполняем требуемые действия — в том же порядке, как и для обычных чисел. А именно:
- Сначала выполняется возведение в степень — избавьтесь от всех выражений, содержащих показатели;
- Затем — деление и умножение;
- Последним шагом выполняется сложение и вычитание.
Разумеется, если в выражении присутствуют скобки, порядок действий изменяется — все, что стоит внутри скобок, надо считать в первую очередь. И помните о неправильных дробях: выделять целую часть надо лишь тогда, когда все остальные действия уже выполнены.
Переведем все дроби из первого выражения в неправильные, а затем выполним действия:

Теперь найдем значение второго выражения. Тут дробей с целой частью нет, но есть скобки, поэтому сначала выполняем сложение, и лишь затем — деление. Заметим, что 14 = 7 · 2 . Тогда:
Наконец, считаем третий пример. Здесь есть скобки и степень — их лучше считать отдельно. Учитывая, что 9 = 3 · 3 , имеем:
Обратите внимание на последний пример. Чтобы возвести дробь в степень, надо отдельно возвести в эту степень числитель, и отдельно — знаменатель.
Можно решать по-другому. Если вспомнить определение степени, задача сведется к обычному умножению дробей:
![]()
Многоэтажные дроби
До сих пор мы рассматривали лишь «чистые» дроби, когда числитель и знаменатель представляют собой обыкновенные числа. Это вполне соответствует определению числовой дроби, данному в самом первом уроке.
Но что, если в числителе или знаменателе разместить более сложный объект? Например, другую числовую дробь? Такие конструкции возникают довольно часто, особенно при работе с длинными выражениями. Вот пара примеров:
Правило работы с многоэтажными дробями всего одно: от них надо немедленно избавляться. Удалить «лишние» этажи довольно просто, если вспомнить, что дробная черта означает стандартную операцию деления. Поэтому любую дробь можно переписать следующим образом:
Пользуясь этим фактом и соблюдая порядок действий, мы легко сведем любую многоэтажную дробь к обычной. Взгляните на примеры:
Задача. Переведите многоэтажные дроби в обычные:

В каждом случае перепишем основную дробь, заменив разделительную черту знаком деления. Также вспомним, что любое целое число представимо в виде дроби со знаменателем 1. Т.е. 12 = 12/1; 3 = 3/1. Получаем:

В последнем примере перед окончательным умножением дроби были сокращены.
Специфика работы с многоэтажными дробями
В многоэтажных дробях есть одна тонкость, которую всегда надо помнить, иначе можно получить неверный ответ, даже если все вычисления были правильными. Взгляните:
- В числителе стоит отдельное число 7, а в знаменателе — дробь 12/5;
- В числителе стоит дробь 7/12, а в знаменателе — отдельное число 5.
Итак, для одной записи получили две совершенно разных интерпретации. Если подсчитать, ответы тоже будут разными:
Чтобы запись всегда читалась однозначно, используйте простое правило: разделяющая черта основной дроби должна быть длиннее, чем черта вложенной. Желательно — в несколько раз.
Если следовать этому правилу, то приведенные выше дроби надо записать так:
Да, возможно, это некрасиво и занимает слишком много места. Зато вы будете считать правильно. Напоследок — пара примеров, где действительно возникают многоэтажные дроби:
Задача. Найдите значения выражений:

Итак, работаем с первым примером. Переведем все дроби в неправильные, а затем выполним операции сложения и деления:

Аналогично поступим со вторым примером. Переведем все дроби в неправильные и выполним требуемые операции. Чтобы не утомлять читателя, я опущу некоторые очевидные выкладки. Имеем:

Благодаря тому, что в числителе и знаменателе основных дробей стоят суммы, правило записи многоэтажных дробей соблюдается автоматически. Кроме того, в последнем примере мы намеренно оставили число 46/1 в форме дроби, чтобы выполнить деление.
Также отмечу, что в обоих примерах дробная черта фактически заменяет скобки: первым делом мы находили сумму, и лишь затем — частное.
Кто-то скажет, что переход к неправильным дробям во втором примере был явно избыточным. Возможно, так оно и есть. Но этим мы страхуем себя от ошибок, ведь в следующий раз пример может оказаться намного сложнее. Выбирайте сами, что важнее: скорость или надежность.
Дробь — число, которое состоит из целого числа долей единицы и представляется в виде: a/b
Числитель дроби (a) — число, находящееся над чертой дроби и показывающее количество долей, на которые была поделена единица.
Знаменатель дроби (b) — число, находящееся под чертой дроби и показывающее на сколько долей поделили единицу.
2.Приведение дробей к общему знаменателю
3.Арифметические действия над обыкновенными дробями
3.1.Сложение обыкновенных дробей
3.2.Вычитание обыкновенных дробей
3.3.Умножение обыкновенных дробей
3.4.Деление обыкновенных дробей
4.Взаимно обратные числа
5.Десятичные дроби
6.Арифметические действия над десятичными дробями
6.1.Сложение десятичных дробей
6.2.Вычитание десятичных дробей
6.3.Умножение десятичных дробей
6.4.Деление десятичных дробей
#1. Основное свойство дроби
Если числитель и знаменатель дроби умножить или разделить на одно и то же число, не равное нулю, то получится дробь, равная данной.
3/7=3*3/7*3=9/21, то есть 3/7=9/21
a/b=a*m/b*m — так выглядит основное свойство дроби.
Другими словами, мы получим дробь, равную данной, умножив или разделив числитель и знаменатель исходной дроби на одно и то же натуральное число.
Если ad=bc, то две дроби a/b=c/d считаются равными.
Например, дроби 3/5 и 9/15 будут равными, так как 3*15=5*9, то есть 45=45
Сокращение дроби — это процесс замены дроби, при котором новая дробь получается равной исходной, но с меньшим числителем и знаменателем.
Сокращать дроби принято, опираясь на основное свойство дроби.
Например, 45/60=15/20=9/12=3/4(числитель и знаменатель делится на число 3, на 5 и на 15).
Несократимая дробь — это дробь вида 3/4, где числитель и знаменатель являются взаимно простыми числами. Основная цель сокращения дроби — сделать дробь несократимой.
2. Приведение дробей к общему знаменателю
Чтобы привести две дроби к общему знаменателю, надо:
1) разложить знаменатель каждой дроби на простые множители;
2) умножить числитель и знаменатель первой дроби на недостающие
множители из разложения второго знаменателя;
3) умножить числитель и знаменатель второй дроби на недостающие множители из первого разложения.
Примеры: приведите дроби к общему знаменателю .
Разложим знаменатели на простые множители: 18=3∙3∙2, 15=3∙5
Умножили числитель и знаменатель дроби на недостающий множитель 5 из второго разложения.
числитель и знаменатель дроби на недостающие множители 3 и 2 из первого разложения.
![]() = , 90 – общий знаменатель дробей .
= , 90 – общий знаменатель дробей .
3. Арифметические действия над обыкновенными дробями
3.1. Сложение обыкновенных дробей
а) При одинаковых знаменателях числитель первой дроби складывают с числителем второй дроби, оставляя знаменатель прежним. Как видно на примере:
a/b+c/b=(a+c)/b;
б) При разных знаменателях дроби сначала приводят к общему знаменателю, а затем выполняют сложение числителей по правилу а):
7/3+1/4=7*4/12+1*3/12=(28+3)/12=31/12
3.2. Вычитание обыкновенных дробей
а) При одинаковых знаменателях из числителя первой дроби вычитают числитель второй дроби, оставляя знаменатель прежним:
a/b-c/b=(a-c)/b;
б) Если же знаменатели дробей различны, то сначала дроби приводят к общему знаменателю, а затем повторяют действия как в пункте а).
3.3. Умножение обыкновенных дробей
Умножение дробей подчиняется следующему правилу:
a/b*c/d=a*c/b*d,
то есть перемножают отдельно числители и знаменатели.
Например:
3/5*4/8=3*4/5*8=12/40.
3.4. Деление обыкновенных дробей
Деление дробей производят следующим способом:
a/b:c/d=a*d/b*c,
то есть дробь a/b умножается на дробь, обратную данной, то есть умножается на d/c.
Пример: 7/2:1/8=7/2*8/1=56/2=28

4. Взаимно обратные числа
Если a*b=1, то число b является обратным числом для числа a.
Пример: для числа 9 обратным является 1/9, так как 9*1/9=1, для числа 5 — обратное число 1/5, так как 5*1/5=1.
5. Десятичные дроби
Десятичной дробью называется правильная дробь, знаменатель которой равен 10, 1000, 10 000, …, 10^n10,1000,10000,…,10n.
Например: 6/10=0,6; 44/1000=0,044.
Таким же способом пишутся неправильные со знаменателем 10^n или смешанные числа.
Например: 51/10=5,1; 763/100=7,63
В виде десятичной дроби представляется любая обыкновенная дробь со знаменателем, который является делителем некой степени числа 10.
менателем, который является делителем некой степени числа 10.
Пример: 5 — делитель числа 100, поэтому дробь 1/5=1 *20/5*20=20/100=0,20=0,2.
6. Арифметические действия над десятичными дробями
6.1. Сложение десятичных дробей
Для сложения двух десятичных дробей, нужно их расположить так, чтобы друг под другом оказались одинаковые разряды и запятая под запятой, а затем выполнить сложение дробей как обычных чисел.
6.2. Вычитание десятичных дробей
Выполняется аналогично сложению.
6.3. Умножение десятичных дробей
При умножении десятичных чисел достаточно перемножить заданные числа, не обращая внимания на запятые (как натуральные числа), а в полученном ответе запятой справа отделяется столько цифр, сколько их стоит после запятой в обоих множителях суммарно.
Давайте выполним умножение 2,7 на 1,3. Имеем 27 cdot 13=35127⋅13=351. Отделяем справа две цифры запятой (у первого и второго числа — одна цифра после запятой; 1+1=21+1=2). В итоге получаем 2,7 cdot 1,3=3,512,7⋅1,3=3,51.
Если в полученном результате получается меньше цифр, чем надо отделить запятой, то впереди пишут недостающие нули, например:

Для умножения на 10, 100, 1000, надо в десятичной дроби перенести запятую на 1, 2, 3цифры вправо (в случае необходимости справа приписывается определенное число нулей).
Например: 1,47 cdot 10 000 = 14 7001,47⋅10000=14700.
6.4. Деление десятичных дробей
Деление десятичной дроби на натуральное число производят также, как и деление натурального числа на натуральное. Запятая в частном ставится после того, как закончено деление целой части.
Если целая часть делимого меньше делителя, то в ответе получается нуль целых, например:
.png)
Рассмотрим деление десятичной дроби на десятичную. Пусть нужно разделить 2,576 на 1,12. Первым делом, умножим делимое и делитель дроби на 100, то есть перенесем запятую вправо в делимом и делителе на столько знаков, сколько их стоит в делителе после запятой (в данном примере на две). Затем нужно выполнить деление дроби 257,6 на натуральное число 112, то есть задача сводится к уже рассмотренному случаю:
.png)
Бывает так, что не всегда получается конечная десятичная дробь при делении одного числа на другое. В результате получается бесконечная десятичная дробь. В таких случаях переходят к обыкновенным дробям.
Например, 2,8: 0,09= 28/10: 9/100= 28*100/10*9=2800/90=280/9=31 1/9.
Дроби бывают обыкновенные и десятичные. Когда школьник узнает о существовании последних, он начинает при каждом удобном случае переводить все, что возможно, в десятичный вид, даже если этого не требуется.
Как ни странно, у старшеклассников и студентов предпочтения меняются, потому что проще выполнять многие арифметические действия с обыкновенными дробями. Да и значения, с которыми имеют дело выпускники, преобразовать в десятичный вид без потерь порой бывает попросту невозможно. В результате оба вида дробей оказываются, так или иначе, приспособлены к делу и обладают своими преимуществами и недостатками. Посмотрим, как с ними работать.
Определение
Дроби — это те же доли. Если в апельсине десять долек, а вам дали одну, то у вас в руке 1/10 часть фрукта. При такой записи, как в предыдущем предложении, дробь будет называться обыкновенной. Если написать то же самое как 0,1 — десятичной. Оба варианта являются равноправными, однако имеют свои преимущества. Первый вариант удобнее при умножении и делении, второй — при сложении, вычитании и в ряде других случаев.
Как перевести дробь в другой вид
Предположим, у вас есть обыкновенная дробь, и вы хотите сделать из неё десятичную. Что для этого нужно сделать?
К слову сказать, нужно заранее определиться, что не любое число можно без проблем записать в десятичном виде. Иногда приходится результат округлять, теряя некоторое количество знаков после запятой, а во многих областях — например, в точных науках — это совершено непозволительная роскошь. В то же время действия с десятичными и обыкновенными дробями в 5 классе позволяют осуществлять такой перевод из одного вида в другой без помех, хотя бы в качестве тренировки.
Если из знаменателя путём умножения или деления на целое число можно получить значение, кратное 10, перевод пройдёт без каких-либо трудностей: ¾ превращается в 0,75, 13/20 — в 0,65.
Обратная процедура выполняется ещё проще, поскольку из десятичной дроби можно всегда получить обыкновенную без потерь в точности. Например, 0,2 становится 1/5, а 0,08 — 4/25.
Внутренние преобразования
Прежде чем осуществлять совместные действия с обыкновенными дробями, нужно подготовить числа к возможным математическим операциям.
Перво-наперво нужно привести все имеющиеся в примере дроби к одному общему виду. Они должны быть либо обыкновенными, либо десятичными. Сразу оговоримся, что умножение и деление удобнее выполнять с первыми.

В подготовке чисел к дальнейшим действиям вам поможет правило, известное как и используемое как в первые годы изучения предмета, так и в высшей математике, которую изучают в университетах.
Свойства дробей
Предположим, у вас есть некоторое значение. Скажем, 2/3. Что изменится, если вы умножите числитель и знаменатель на 3? Получится 6/9. А если на миллион? 2000000/3000000. Но постойте, ведь число качественно совершенно не меняется — 2/3 остаются равны 2000000/3000000. Меняется только форма, но не содержание. То же самое произойдёт при делении обеих частей на одно и то же значение. В этом и заключается основное свойство дроби, которое неоднократно поможет вам производить действия с десятичными и обыкновенными дробями на контрольных и экзаменах.

Умножение числителя и знаменателя на одно и то же число называется расширением дроби, а деление — сокращением. Надо сказать, что зачеркивание одинаковых чисел в верхней и нижней части при перемножении и делении дробей — удивительно приятная процедура (в рамках урока математики, конечно). Создается впечатление, что ответ уже близок и пример практически решен.
Неправильные дроби
Неправильной дробью называется такая, у которой числитель больше или равен знаменателю. Иными словами, если у неё можно выделить целую часть, она попадает под это определение.
Если такое число (большее либо равное единице) представлено в виде обыкновенной дроби, она будет называться неправильной. А если числитель меньше знаменателя — правильной. Оба вида одинаково удобны при осуществлении возможных действий с обыкновенными дробями. Их можно беспрепятственно умножать и делить, складывать и вычитать.
Если же одновременно выделена целая часть и при этом имеется остаток в виде дроби, полученное число будет называться смешанным. В будущем вы столкнетесь с различными способами комбинации таких структур с переменными, а также решением уравнений, где потребуются эти знания.
Арифметические операции
Если с основным свойством дроби всё ясно, то как вести себя при перемножении дробей? Действия с обыкновенными дробями в 5 классе подразумевают все виды арифметических операций, которые выполняются двумя различными способами.
Умножение и деление выполняются очень просто. В первом случае просто перемножаются числители и знаменатели двух дробей. Во втором — то же самое, только крест-накрест. Таким образом, числитель первой дроби умножается на знаменатель второй, и наоборот.

Для выполнения сложения и вычитания нужно произвести дополнительное действие — привести все компоненты выражения к общему знаменателю. Это значит, что нижние части дробей должны быть изменены до одинакового значения — числа, кратного обоим имеющимся знаменателям. Например, для 2 и 5 это будет 10. Для 3 и 6 — 6. Но что тогда делать с верхней частью? Мы же не можем оставить её в прежнем виде, если изменили нижнюю. Согласно основному свойству дроби мы умножим числитель на то же число, что и знаменатель. Эта операция должна быть произведена с каждым из чисел, которые мы будем складывать или вычитать. Впрочем, такие действия с обыкновенными дробями в 6 классе выполняются уже «на автомате», а трудности возникают только на начальном этапе изучения темы.
Сравнение
Если у двух дробей одинаковый знаменатель, то больше будет та из них, числитель которой больше. Если же одинаковы верхние части, то больше будет та, у которой меньше знаменатель. Стоит иметь в виду, что столь удачные ситуации для сравнения выпадают нечасто. Скорее всего, и верхние, и нижние части выражений совпадать не будут. Тогда понадобится вспомнить про возможные действия с обыкновенными дробями и использовать приём, применяемый при сложении и вычитании. Кроме того, помните, что если мы говорим об отрицательных числах, то большая по модулю дробь окажется меньшей.
Преимущества обыкновенных дробей
Случается, что преподаватели говорят детям одну фразу, содержание которой можно выразить так: чем больше информации дано при формулировке задания, тем проще будет решение. Кажется, что звучит странно? Но действительно: при большом количестве известных величин можно пользоваться практически любыми формулами, а вот если предоставлена лишь пара чисел, могут потребоваться дополнительные размышления, придётся вспоминать и доказывать теоремы, приводить аргументы в пользу своей правоты…

К чему мы это? Да к тому, что обыкновенные дроби при всей своей громоздкости могут сильно упростить жизнь ученику, позволяя при перемножении и делении сокращать целые строки значений, а при расчёте суммы и разности выносить общие аргументы и, опять же, сокращать их.
Когда требуется осуществить совместные действия с обыкновенными и десятичными дробями, трансформации осуществляются в пользу первых: как вы переведете 3/17 в десятичный вид? Только с потерями информации, не иначе. А вот 0,1 можно представить как 1/10, а далее — как 17/170. И тогда два получившихся числа можно складывать или вычитать: 30/170 + 17/170 = 47/170.
Чем полезны десятичные дроби
Если действия с обыкновенными дробями осуществлять и сподручнее, то записывать все с их помощью крайне неудобно, десятичные здесь имеют существенное преимущество. Сравните: 1748/10000 и 0,1748. Это одно и то же значение, представленное в двух различных вариантах. Разумеется, второй способ проще!
Кроме того, десятичные дроби проще представить, поскольку все данные имеют общее основание, различающееся исключительно на порядки. Скажем, скидку в 30% мы легко осознаем и даже оценим как значительную. А сразу ли вы поймете, что больше — 30% или 137/379? Таким образом, десятичные дроби обеспечивают стандартизацию расчётов.

В старших классах ученики решают квадратные уравнения. Выполнять действия с обыкновенными дробями здесь уже крайне проблематично, поскольку формула для расчёта значений переменной содержит квадратный корень из суммы. При наличии дроби, не сводимой к десятичной, решение усложняется настолько, что рассчитать точный ответ без калькулятора становится практически невозможно.
Итак, каждый способ представления дробей имеет свои преимущества в соответствующем контексте.
Формы записи
Существует два способа записи действий с обыкновенными дробями: через горизонтальную черту, в два «яруса», и через наклонную черту (она же — «слэш») — в строку. Когда ученик пишет в тетради, первый вариант обычно удобнее, а потому и более распространен. Распределение рядом цифр по клеточкам способствует развитию внимательности при расчётах и проведении преобразований. При записи в строку можно по невнимательности перепутать порядок действий, потерять какие-либо данные — то есть, ошибиться.

Достаточно часто в наше время возникает необходимость напечатать числа на компьютере. Разделять дроби традиционной горизонтальной чертой можно, используя функцию в программе «Майкрософт Ворд» 2010 и более позднего года выпуска. Дело в том, что в этих версиях софта есть опция под названием «формула». Она выводит на экран прямоугольное трансформируемое поле, в рамках которого можно комбинировать любые математические символы, составлять и двух-, и «четырехэтажные» дроби. В знаменателе и числителе можно пользоваться скобками, знаками операций. В результате вы сможете записать любые совместные действия с обыкновенными и десятичными дробями в традиционной форме, т. е. так, как это учат делать в школе.
Если же вы будете пользоваться стандартным текстовым редактором «Блокнот», то все дробные выражения нужно будет писать через наклонную черту. Другого способа здесь, к сожалению, не предусмотрено.
Заключение
Вот мы и рассмотрели все основные действия с обыкновенными дробями, которых, оказывается, не так уж и много.
Если поначалу может казаться, что это сложный раздел математики, то это только временное впечатление — помните, когда-то вы так думали про таблицу умножения, а ещё раньше — про обычные прописи и счёт от одного до десяти.
Важно понимать, что дроби используются в повседневной жизни повсюду. Вы будете иметь дело с деньгами и инженерными расчётами, информационными технологиями и музыкальной грамотой, и везде — везде! — дробные числа будут фигурировать. Поэтому не поленитесь и изучите эту тему хорошенько — тем более не такая уж она и сложная.
496. Найти х, если:
497. 1) Если к 3 / 10 неизвестного числа прибавить 10 1 / 2 , то получится 13 1 / 2 . Найти неизвестное число.
2) Если от 7 / 10 неизвестного числа вычесть 10 1 / 2 , то получится 15 2 / 5 . Найти неизвестное число.
498*. Если из 3 / 4 неизвестного числа вычесть 10 и полученную разность умножить на 5, то получится 100. Найти число.
499*. Если неизвестное число увеличить на 2 / 3 его, то получится 60. Какое это число?
500*. Если к неизвестному числу прибавить столько же, да ещё 20 1 / 3 , то получится 105 2 / 5 . Найти неизвестное число.
501.1) Урожай картофеля при квадратно-гнездовой посадке составляет в среднем 150 ц с 1 га, а при обычной посадке 3 / 5 этого количества. На сколько больше можно собрать картофеля с площади в 15 га, если посадку картофеля производить квадратно-гнездовым способом?
2) Опытный рабочий изготовил за 1 час 18 деталей, а малоопытный 2 / 3 этого количества. На сколько больше деталей изготовит опытный рабочий за 7-часовой рабочий день?
502. 1) Пионеры собрали в течение трёх дней 56 кг разных семян. В первый день было собрано 3 / 14 всего количества, во второй- в полтора раза больше, а в третий день-остальное зерно. Сколько килограммов семян собрали пионеры в третий день?
2) При размоле пшеницы получилось: муки 4 / 5 всего количества пшеницы, манной крупы — в 40 раз меньше, чем муки, а остальное- отруби. Сколько муки, манной крупы и отрубей в отдельности получилось при размоле 3 т пшеницы?
503.1) В трёх гаражах помещается 460 машин. Число машин, помещающихся в первом гараже, составляет 3 / 4 числа машин, помещающихся во втором, а в третьем гараже в 1 1 / 2 раза больше машин, чем в первом. Сколько машин помещается в каждом гараже?
2) На заводе, имеющем три цеха, работает 6 000 рабочих. Во втором цехе работает в 1 1 / 2 раза меньше, чем в первом, а число рабочих третьего цеха составляет 5 / 6 числа рабочих второго цеха. Сколько рабочих в каждом цехе?
504. 1) Из резервуара с керосином отлили вначале 2 / 5 , потом 1 / 3 всего керосина и после этого в резервуаре осталось 8 т керосина. Сколько керосина было в резервуаре первоначально?
2) Велосипедисты вели гонку в течение трёх дней. В первый день они проехали 4 / 15 всего пути, во второй — 2 / 5 , а в третий день оставшиеся 100 км. Какой путь проехали велосипедисты за три дня?
505. 1) Ледокол три дня пробивался через ледяное поле. В первый день он прошел 1 / 2 всего пути, во второй день 3 / 5 оставшегося пути и в третий день остальные 24 км. Найти длину пути, пройденного ледоколом за три дня.
2) Три отряда школьников производили посадку деревьев по озеленению села. Первый отряд посадил 7 / 20 всех деревьев, второй 5 / 8 оставшихся деревьев, а третий остальные 195 деревьев. Сколько всего деревьев посадили три отряда?
506. 1) Комбайнер убрал урожай пшеницы с одного участка за три дня. В первый день он убрал урожай с 5 / 18 всей площади участка, во второй день с 7 / 13 оставшейся площади и в третий день — с остальной площади в 30 1 / 2 га. В среднем с каждого гектара собрано 20 ц пшеницы. Сколько пшеницы было собрано на всём участке?
2) Участники автопробега в первый день прошли 3 / 11 всего пути, во второй день 7 / 20 оставшегося пути, в третий день 5 / 13 нового остатка, а в четвёртый день-остальные 320 км. Как велик путь автопробега?
507. 1) Автомобиль прошёл в первый день 3 / 8 всего пути, во второй 15 / 17 того, что прошел в первый, и в третий день остальные 200 км. Сколько бензина было израсходовано, если на 10 км пути автомобиль расходует 1 3 / 5 кг бензина?
2) Город состоит из четырёх районов. И первом районе живёт 4 / 13 всех жителей города, во втором 5 / 6 числа жителей первого района, в третьем 4 / 11 числа жителей первых; двух районов вместе взятых, а в четвёртом районе живет 18 тысяч человек. Сколько хлеба требуется всему населению города на 3 дня, если в среднем один человек потребляет 500 г в день?
508.1) Турист прошёл в первый день 10 / 31 всего пути, во второй 9 / 10 того, что прошёл в первый день, а в третий остальную часть пути, причём в третий день он прошёл на 12 км больше, чем во второй день. Сколько километров прошёл турист в каждый из трёх дней?
2) Весь путь от города А до города Б автомобиль прошёл за три дня. В первый день автомобиль прошёл 7 / 20 всего пути, во второй 8 / 13 оставшегося пути, а в третий день автомобиль прошёл на 72 км меньше, чем в первый день. Каково расстояние между городами А и Б?
509.1) Исполком отвёл землю рабочим трёх заводов под садовые участки. Первому заводу было отведено 9 / 25 всего количества участков, второму заводу 5 / 9 числа участков, отведённых для первого, а третьему — остальные участки. Сколько всего участков было отведено рабочим трёх заводов, если первому заводу было отведено на 50 участков меньше, чем третьему?
2) Самолёт доставил смену зимовщиков на полярную станцию из Москвы за три дня. В первый день он пролетел 2 / 5 всего пути, во второй — 5 / 6 пути, пройденного им за первый день, а в третий день он пролетел на 500 км меньше, чем во второй день. Какое расстояние пролетел самолёт за три дня?
510.1) Завод имел три цеха. Число рабочих первого цеха составляет 2 / 5 всех рабочих завода; во втором цехе рабочих в 1 1 / 2 раза меньше, чем в первом, а в третьем цехе на 100 рабочих больше, чем во втором. Сколько всего рабочих на заводе?
2) В колхоз входят жители трёх соседних сёл. Число семей первого села составляет 3 / 10 всех семей колхоза; во втором селе число семей в 1 1 / 2 раза больше, чем в первом, а в третьем селе число семей на 420 меньше, чем во втором. Сколько всего семей в колхозе?
511. 1) Артель израсходовала в первую неделю 1 / 3 имевшегося у неё запаса сырья, а во вторую 1 / 3 остатка. Сколько сырья осталось в артели, если в первую неделю расход сырья был на 3 / 5 т больше, чем во вторую неделю?
2) Из завезённого угля для отопления дома в первый месяц было израсходовано 1 / 6 его часть, а во второй месяц — 3 / 8 остатка. Сколько угля осталось для отопления дома, если во второй месяц было израсходовано на 1 3 / 4 больше, чем в первый месяц?
512. 3 / 5 всей земли колхоза отведено под посев зерна, 13 / 36 остатка занято огородами и лугом, остальная земля — лесом, причём посевная площадь колхоза на 217 га больше площади леса, 1 / 3 земли, отведенной под посевы зерна, засеяна рожью, а остальная-пшеницей. Сколько гектаров земли засеял колхоз пшеницей и сколько рожью?
513. 1) Трамвайный маршрут имеет в длину 14 3 / 8 км. На протяжении этого маршрута трамвай делает 18 остановок, затрачивая в среднем на каждую остановку до 1 1 / 6 мин. Средняя скорость движения трамвая на всём маршруте 12 1 / 2 км в час. Сколько времени требуется трамваю для совершения одного рейса?
2) Маршрут автобуса 16 км. На протяжении этого маршрута автобус делает 36 остановок по 3 / 4 мин. в среднем каждая. Средняя скорость автобуса 30 км в час. Сколько времени требуется автобусу на один маршрут?
514*. 1) Сейчас 6 час. вечера. Какую часть составляет оставшаяся часть суток от прошедшей и какая часть суток осталась?
2) Пароход по течению проходит расстояние между двумя городами за 3 сут. и обратно это же расстояние за 4 сут. Сколько суток будут плыть по течению плоты от одного города до другого?
515. 1) Сколько досок пойдёт на настилку пола в комнате, длина которой 6 2 / 3 м, ширин.ч 5 1 / 4 м, если длина каждой доски 6 2 / 3 м, а ее ширина составляет 3 / 80 длины?
2) Площадка прямоугольной формы имеет длину 45 1 / 2 м, а её ширина составляет 5 / 13 длины. Эту площадку окаймляет дорожка шириной 4 / 5 м. Найти площадь дорожки.
516. Найти среднее арифметическое чисел:

517. 1) Среднее арифметическое двух чисел 6 1 / 6 . Одно из чисел 3 3 / 4 . Найти другое число.
2) Среднее арифметическое двух чисел 14 1 / 4 . Одно из этих чисел 15 5 / 6 . Найти другое число.
518. 1) Товарный поезд был в пути три часа. За первый час он прошёл 36 1 / 2 км, за второй 40 км и за третий 39 3 / 4 км. Найти среднюю скорость поезда.
2) Автомобиль за первых два часа прошёл 81 1 / 2 км, а за следующие 2 1 / 2 часа 95 км. Сколько километров в среднем он проходил в час?
519.1) Тракторист выполнил задание по вспашке земли за три дня. В первый день он вспахал 12 1 / 2 га, во второй день 15 3 / 4 га и в третий день 14 1 / 2 га. Сколько в среднем гектаров земли вспахал тракторист за день?
2) Отряд школьников, совершая туристский трёхдневный поход, находился в пути в первый день 6 1 / 3 часа, во второй 7 час. и в третий день — 4 2 / 3 часа. Сколько часов в среднем находились ежедневно в пути школьники?
520.1) В доме живут три семьи. Первая семья для освещения квартиры имеет 3 электрические лампочки, вторая 4 и третья 5 лампочек. Сколько должна заплатить каждая семья за электроэнергию, если все лампы были одинаковы, а общий счет (на весь дом) оплаты электроэнергии был 7 1 / 5 руб.?
2) Полотёр натирал полы в квартире, где жили три семьи. Первая семья имела жилую площадь в 36 1 / 2 кв. м, вторая в 24 1 / 2 кв. м, а третья — в 43 кв. м. За всю работу было уплачено 2 руб. 08 коп. Сколько уплатила каждая семья?
521. 1) На огородном участке собрано картофеля с 50 кустов по 1 1 / 10 кг с одного куста, с 70 кустов по 4 / 5 кг с одного куста, с 80 кустов по 9 / 10 кг с одного куста. Сколько килограммов картофеля в среднем собрано с каждого куста?
2) Полеводческая бригада на площади в 300 га получила урожай по 20 1 / 2 ц озимой пшеницы с 1 га, с 80 га по 24 ц с 1 га и с 20 га — по 28 1 / 2 ц с 1 га. Чему равен средний урожай в бригаде с 1 га?
522.1) Сумма двух чисел 7 1 / 2 . Одно число больше другого нa 4 4 / 5 . Найти эти числа.
2) Если сложить числа, выражающие ширину Татарского и ширину Керченского проливов вместе, то получим 11 7 / 10 км. Татарский пролив на 3 1 / 10 км шире Керченского. Какова ширина каждого пролива?
523. 1) Сумма трёх чисел 35 2 / 3 . Первое число больше второго на 5 1 / 3 и больше третьего на 3 5 / 6 . Найти эти числа.
2) Острова Новая Земля, Сахалин и Северная Земля вместе занимают площадь 196 7 / 10 тыс. кв. км. Площадь Новой Земли на 44 1 / 10 тыс. кв. км больше площади Северной Земли и на 5 1 / 5 тыс. кв. км больше площади Сахалина. Какова площадь каждого из перечисленных островов?
524. 1) Квартира состоит из трех комнат. Площадь первой комнаты 24 3 / 8 кв. м и составляет 13 / 36 всей площади квартиры. Площадь второй комнаты на 8 1 / 8 кв. м больше, чем площадь третьей. Какова площадь второй комнаты?
2) Велосипедист во время трёхдневных соревнований в первый день был в пути 3 1 / 4 часа, что составляло 13 / 43 всего времени в пути. Во второй день он ехал на 1 1 / 2 часа больше, чем в третий день. Сколько часов велосипедист был в пути во второй день соревнований?
525. Три куска железа весят вместе 17 1 / 4 кг. Если вес первого куска уменьшить на 1 1 / 2 кг, вес второго на 2 1 / 4 кг, то все три куска будут иметь одинаковый вес. Сколько весил каждый кусок железа?
526.1) Сумма двух чисел 15 1 / 5 . Если первое число уменьшить на 3 1 / 10 , а второе увеличить на 3 1 / 10 , то эти числа будут равны. Чему равно каждое число?
2) В двух ящиках было 38 1 / 4 кг крупы. Если из одного ящика пересыпать в другой 4 3 / 4 кг крупы, то в обоих ящиках станет крупы поровну. Сколько крупы в каждом ящике?
527. 1) Сумма двух чисел равна 17 17 / 30 . Если от первого числа вычесть 5 1 / 2 и прибавить ко второму, то первое будет всё-таки больше второго на 2 17 / 30 . Найти оба числа.
2) В двух ящиках 24 1 / 4 кг яблок. Если из первого ящика переложить во второй 3 1 / 2 кг, то в первом всё-таки будет яблок на 3 / 5 кг больше, чем во втором. Сколько килограммов яблок в каждом ящике?
528*. 1) Сумма двух чисел 8 11 / 14 , а разность их 2 3 / 7 . Найти эти числа.
2) Катер по течению реки шёл со скоростью 15 1 / 2 км в час, а против течения 8 1 / 4 км в час. Какова скорость течения реки?
529. 1) В двух гаражах 110 машин, причём в одном из них в 1 1 / 5 раза больше, чем в другом. Сколько машин в каждом гараже?
2) Жилая площадь квартиры, состоящей из двух комнат, равна 47 1 / 2 кв. м. Площадь одной комнаты составляет 8 / 11 площади другой. Найти площадь каждой комнаты.
530. 1) Сплав, состоящий из меди и серебра, весит 330 г. Вес меди в этом сплаве составляет 5 / 28 веса серебра. Сколько в сплаве серебра и сколько меди?
2) Сумма двух чисел 6 3 / 4 , а частное 3 1 / 2 . Найти эти числа.
531. Сумма трёх чисел 22 1 / 2 . Второе число в 3 1 / 2 раза, а третье в 2 1 / 4 раза больше первого. Найти эти числа.
532. 1) Разность двух чисел 7; частное от деления большего числа на меньшее 5 2 / 3 . Найти эти числа.
2) Разность двух чисел 29 3 / 8 , а кратное отношение их равно 8 5 / 6 . Найти эти числа.
533. В классе число отсутствующих учеников равно 3 / 13 числа присутствующих. Сколько учеников в классе по списку, если присутствует на 20 человек больше, чем отсутствует?
534. 1) Разность двух чисел 3 1 / 5 . Одно число составляет 5 / 7 другого. Найти эти числа.
2) Отец старше сына на 24 года. Число лет сына равно 5 / 13 числа лет отца. Сколько лет отцу и сколько сыну?
535. Знаменатель дроби на 11 единиц больше её числителя. Чему равна дробь, если её знаменатель в 3 3 / 4 раза больше числителя?
№ 536 — 537 устно.
536.1) Первое число составляет 1 / 2 второго. Во сколько раз второе число больше первого?
2) Первое число составляет 3 / 2 второго. Какую часть первого числа составляет второе число?
537.1) 1 / 2 первого числа равна 1 / 3 второго числа. Какую часть первого числа составляет второе число?
2) 2 / 3 первого числа равны 3 / 4 второго числа. Какую часть первого числа составляет второе число? Какую часть второго числа составляет первое?
538. 1) Сумма двух чисел равна 16. Найти эти числа, если 1 / 3 второго числа равна 1 / 5 первого.
2) Сумма двух чисел равна 38. Найти эти числа, если 2 / 3 первого числа равны 3 / 5 второго.
539*. 1) Два мальчика собрали вместе 100 грибов. 3 / 8 числа грибов, собранных первым мальчиком, численно равны 1 / 4 числа грибов, собранных вторым мальчиком. Сколько грибов собрал каждый мальчик?
2) В учреждении работает 27 человек. Сколько работает мужчин и сколько женщин, если 2 / 5 числа всех мужчин равны 3 / 5 числа всех женщин?
540*. Три мальчика купили волейбольный мяч. Определить взнос каждого мальчика, зная, что 1 / 2 взноса первого мальчика равна 1 / 3 взноса второго, или 1 / 4 взноса третьего, и что взнос третьего мальчика больше взноса первого на 64 коп.
541*. 1) Одно число больше другого на 6. Найти эти числа, если 2 / 5 одного числа равны 2 / 3 другого.
2) Разность двух чисел равна 35. Найти эти числа, если 1 / 3 первого числа равна 3 / 4 второго числа.
542.1) Первая бригада может выполнить некоторую работу за 36 дней, а вторая за 45 дней. За сколько дней обе бригады, работая вместе, выполнят эту работу?
2) Пассажирский поезд проходит расстояние между двумя городами за 10 час, а товарный это расстояние проходит за 15 час. Оба поезда вышли одновременно из этих городов навстречу друг другу. Через сколько часов они встретятся?
543. 1) Скорый поезд проходит расстояние между двумя городами за 6 1 / 4 часа, а пассажирский за 7 1 / 2 часа. Через сколько часов встретятся эти поезда, если они выйдут из обоих городов одновременно навстречу друг другу? (Ответ округлить с точностью до 1 часа.)
2) Два мотоциклиста выехали одновременно из двух городов навстречу друг другу. Один мотоциклист может проехать всё расстояние между этими городами за 6 час, а другой за 5 час. Через сколько часов после выезда встретятся мотоциклисты? (Ответ округлить с точностью до 1 часа.)
544. 1) Три автомобиля различной грузоподъёмности могут перевезти некоторый груз, работая отдельно: первый за 10 час, второй за 12 час. и третий за 15 час За сколько часов они могут перевезти тот же груз, работая совместно?
2) Из двух станций выходят одновременно навстречу друг другу два поезда: первый поезд проходит расстояние между этими станциями за 12 1 / 2 часа, а второй за 18 3 / 4 часа. Через сколько часов после выхода поезда встретятся?
545. 1) К ванне подведены два крана. Через один из них ванна может наполниться за 12 мин., через другой в 1 1 / 2 раза быстрее. За сколько минут наполнится 5 / 6 всей ванны, если открыть сразу оба крана?
2) Две машинистки должны перепечатать рукопись. Первая ашинистка может выполнить эту работу зa 3 1 / 3 дня, а вторая в 1 1 / 2 раза быстрее. Во сколько дней выполнят работу обе машинистки, если они будут работать одновременно?
546. 1) Бассейн наполняется первой трубой за 5 час, а через вторую трубу он может быть опорожнен за 6 час Через сколько часов будет наполнен весь бассейн, если одновременно открыть обе трубы?
Указание. За час бассейн наполняется на (1 / 5 — 1 / 6 своей ёмкости.)
2) Два трактора вспахали поле за 6 час. Первый трактор, работая один, мог бы вспахать это поле за 15 час За сколько часов вспахал бы это поле второй трактор, работая один?
547*. Из двух станций выходят одновременно навстречу друг другу два поезда и встречаются через 18 час. после своего выхода. За сколько времени второй поезд проходит расстояние между станциями, если первый поезд проходит это расстояние за 1 сутки 21 час?
548*. Бассейн наполняется двумя трубами. Сначала открыли первую трубу, а затем через 3 3 / 4 часа, когда наполнилась половина бассейна, открыли вторую трубу. Через 2 1 / 2 часа совместной работы бассейн наполнился. Определить вместимость бассейна, если через вторую трубу вливалось 200 вёдер воды в час.
549.1) Из Ленинграда в Москву вышел курьерский поезд, который проходит 1 км за 3 / 4 мин. Через 1 / 2 часа после выхода этого поезда из Москвы в Ленинград вышел скорый поезд, скорость которого была равна 3 / 4 скорости курьерского. На каком расстоянии будут поезда друг от друга через 2 1 / 2 часа после выхода курьерского поезда, если расстояние между Москвой и Ленинградом 650 км?
2) От колхоза до города 24 км. Из колхоза выехала грузовая машина, которая проходит 1 км за 2 1 / 2 мин. Через 15 мин. после выезда этой машины из города в колхоз выехал велосипедист, со скоростью вдвое меньшей, чем скорость грузовой машины. Через сколько времени после своего выезда велосипедист встретится с грузовой машиной?
550. 1) Из одного селения вышел пешеход. Через 4 1 / 2 часа после выхода пешехода по тому же направлению выехал велосипедист, скорость которого в 2 1 / 2 раза больше скорости пешехода. Через сколько часов после выхода пешехода его догонит велосипедист?
2) Скорый поезд проходит 187 1 / 2 км за 3 часа, а товарный поезд 288 км за 6 час. Через 7 1 / 4 часа после выхода товарного поезда по тому же направлению отправляется скорый. Через сколько времени скорый поезд догонит товарный?
551. 1) Из двух колхозов, через которые проходит дорога в районный центр, выехали одновременно в район на лошадях два колхозника. Первый из них проезжал в час по 8 3 / 4 км, а второй в 1 1 / 7 раза больше первого. Второй колхозник нагнал первого через 3 4 / 5 часа. Определить расстояние между колхозами.
2) Через 26 1 / 3 часа после выхода поезда Москва-Владивосток, средняя скорость которого 60 км в час, вылетел по тому же направлению самолёт ТУ-104, со скоростью в 14 1 / 6 раза большей скорости поезда. Через сколько часов после своего вылета самолёт нагонит поезд?
552. 1) Расстояние между городами по реке 264 км. Это расстояние пароход прошёл по течению за 18 час, затратив 1 / 12 этого времени на остановки. Скорость течения реки 1 1 / 2 км в час. За сколько времени прошёл бы пароход без остановок 87 км в стоячей воде?
2) Моторная лодка прошла 207 км по течению реки за 13 1 / 2 часа, затратив 1 / 9 этого времени на остановки. Скорость течения реки 1 3 / 4 км в час. Сколько километров может пройти эта лодка в стоячей воде за 2 1 / 2 часа?
553. Катер по водохранилищу прошёл расстояние в 52 км без остановок за 3 часа 15 мин. Далее, идя по реке против течения, скорость которого 1 3 / 4 км в час, этот катер прошел 28 1 / 2 км за 2 1 / 4 часа, сделав при этом 3 равные по времени остановки. Сколько минут стоял катер на каждой остановке?
554. Из Ленинграда в Кронштадт в 12 час. дня вышел пароход и прошёл всё расстояние между этими городами за 1 1 / 2 часа. По дороге он встретил другой пароход, вышедший из Кронштадта в Ленинград в 12 час 18 мин. и шедший со скоростью в 1 1 / 4 раза большей, чем первый. В котором часу произошла встреча обоих пароходов?
555. Поезд должен был пройти расстояние в 630 км за 14 час. Пройдя 2 / 3 этого расстояния, он был задержан на 1 час 10 мин. С какой скоростью он должен продолжать путь, чтобы прийти к месту назначения без опоздания?
556.В 4 часа 20 мин. утра из Киева в Одессу вышел товарный поезд со средней скоростью 31 1 / 5 км в час. Через некоторое время навстречу ему из Одессы вышел почтовый поезд, скорость которого в 1 17 / 39 Раза больше скорости товарного, ивстретился с товарным поездом через 6 1 / 2 часа после своего выхода. В котором часу вышел из Одессы почтовый поезд, если расстояние между Киевом и Одессой 663 км?
557*. Часы показывают полдень. Через сколько времени часовая и минутная стрелки совпадут?
558. 1) Завод имеет три цеха. Число, рабочих первого цеха составляет 9 / 20 всех рабочих завода, во втором цехе рабочих в 1 1 / 2 раза меньше, чем в первом, а в третьем цехе на 300 рабочих меньше, чем во втором. Сколько всего рабочих на заводе?
2) В городе три средние школы. Число учащихся первой школы составляет 3 / 10 всех учащихся этих трех школ; во второй школе учащихся в 1 1 / 2 раза больше, чем в первой, а в третьей школе на 420 учащихся меньше, чем во второй. Сколько всего учащихся в трёх школах?
559. 1) Два комбайнера работали на одном участке. После того как один комбайнер убрал 9 / 16 всего участка, а второй 3 / 8 того же участка, оказалось, что первый комбайнер убрал на 97 1 / 2 га больше, чем второй. В среднем с каждого гектара намолачивали по 32 1 / 2 ц зерна. Сколько центнеров зерна намолотил каждый комбайнер?
2) Два брата купили фотоаппарат. У одного было 5 / 8 , а у второго 4 / 7 стоимости фотоаппарата, причём у первого было на 2 руб. 25 коп. больше, чем у второго. Каждый уплатил половину стоимости аппарата. Сколько денег осталось у каждого?
560. 1) Из города А в город Б, расстояние между которыми 215 км, вышел легковой автомобиль со скоростью 50 км в час. Одновременно с ним из города Б в город А вышел грузовой автомобиль. Сколько километров прошёл легковой автомобиль до встречи с грузовым, если скорость движения грузового в час составляла 18 / 25 скорости легкового автомобиля?
2) Между городами А и Б 210 км. Из города А в город Б вышла легковая машина. Одновременно с ней из города Б в город А вышла грузовая машина. Сколько километров прошла грузовая машина до встречи с легковой, если легковая машина шла со скоростью 48 км в час, а скорость грузовой машины в час составляла 3 / 4 от скорости легковой машины?
561. Колхоз собрал урожай пшеницы и ржи. Пшеницей было засеяно на 20 га больше, чем рожью. Общий сбор ржи составил 5 / 6 всего сбора пшеницы при урожайности в 20 ц с 1 га как для пшеницы, так и для ржи. 7 / 11 всего сбора пшеницы и ржи колхоз продал государству, а остальной хлеб оставил для удовлетворения своих нужд. Сколько потребовалось совершить рейсов двухтонным машинам для вывоза проданного государству хлеба?
562. На хлебозавод привезли ржаную и пшеничную муку. Вес пшеничной муки составил 3 / 5 веса ржаной муки, причём ржаной муки было привезено на 4 т больше, чем пшеничной. Сколько пшеничного и сколько ржаного хлеба будет выпечено хлебозаводом из этой муки, если припёк составляет 2 / 5 всей муки?
563.В течение трёх дней бригада рабочих выполнила 3 / 4 всей работы по ремонту шоссе между двумя колхозами. В первый день было отремонтировано 2 2 / 5 км этого шоссе, во второй день в 1 1 / 2 раза больше, чем в первый, а в третий день 5 / 8 того, что было отремонтировано в первые два дня вместе. Найти длину шоссе между колхозами.
564. Заполнить свободные места в таблице, где S — площадь прямоугольника, а — основание прямоугольника, a h -высота (ширина) прямоугольника.

565. 1) Длина прямоугольного участка земли 120 м, а ширина участка — 2 / 5 его длины. Найти периметр и площадь участка.
2) Ширина прямоугольного участка 250 м, а длина его в 1 1 / 2 раза больше ширины. Найти периметр и площадь участка.
566. 1) Периметр прямоугольника 6 1 / 2 дм, основание его на 1 / 4 дм больше высоты. Найти площадь этого прямоугольника.
2) Периметр прямоугольника 18 см, высота его на 2 1 / 2 см меньше основания. Найти площадь прямоугольника.
567. Вычислить площади фигур, изображённых на рисунке 30, разбив их на прямоугольники и найдя измерением размеры прямоугольника.

568. 1) Сколько листов сухой штукатурки потребуется для обивки потолка комнаты, длина которой 4 1 / 2 м, а ширина 4 м, если размеры листа штукатурки 2 м х l 1 / 2 м?
2) Сколько досок длиной в 4 1 / 2 л и шириной в 1 / 4 м потребуется для настила пола, длина которого 4 1 / 2 м, а ширина 3 1 / 2 м?
569. 1) Участок прямоугольной формы длиной 560 м, а шириной 3 / 4 его длины, засеяли фасолью. Сколько семян потребовалось для засева участка, если на 1 га высевали 1 ц?
2) С поля прямоугольной формы собрали урожай пшеницы по 25 ц с 1 га. Сколько было собрано пшеницы со всего поля, если длина поля 800 м, а ширина равна 3 / 8 его длины?
570. 1) Прямоугольный участок земли, имеющий в длину 78 3 / 4 м и в ширину 56 4 / 5 м, застроен так, что 4 / 5 его площади занято строениями. Определить площадь земли под строениями.
2) На прямоугольном участке земли, длина которого 9 / 20 км, а ширина составляет 4 / 9 его длины, колхоз предполагает разбить сад. Сколько деревьев будет посажено в этом саду, если под каждое дерево в среднем нужно отвести площадь в 36 кв.м?
571. 1) Для нормального освещения дневным светом комнаты необходимо, чтобы площадь всех окон была не менее 1 / 5 части площади пола. Определить, достаточно ли света в комнате, длина которой 5 1 / 2 м и ширина 4 м. Комната имеет одно окно размером 1 1 / 2 м х 2м?
2) Используя условие предыдущей задачи, выясните, достаточно ли света в вашем классе.
572. 1) Сарай имеет размеры 5 1 / 2 м х 4 1 / 2 м х 2 1 / 2 м. Сколько сена (по весу) поместится в этом сарае, если его наполнить на 3 / 4 его высоты и если 1 куб. м сена весит 82 кг?
2) Поленница дров имеет форму прямоугольного параллелепипеда, размеры которого 2 1 / 2 м х 3 1 / 2 м х 1 1 / 2 м. Каков вес поленницы, если 1 куб. м дров весит 600 кг?
573. 1) Аквариум прямоугольной формы наполнен водой до 3 / 5 высоты. Длина аквариума 1 1 / 2 м, ширина 4 / 5 м, высота 3 / 4 м. Сколько литров воды налито в аквариум?
2) Бассейн, имеющий форму прямоугольного параллелепипеда, имеет длину 6 1 / 2 м, ширину 4м и высоту 2 м. Бассейн наполнен водой до 3 / 4 его высоты. Вычислить количество воды, налитой в бассейн.
574. Вокруг прямоугольного участка земли, длина которого 75 м и ширина 45 м, надо построить забор. Сколько кубометров досок должно пойти на его устройство, если толщина доски 2 1 / 2 см, а высота забора должна быть 2 1 / 4 м?
575. 1) Какой угол составляет минутная и часовая стрелка в 13 час? в 15 час? в 17 час? в 21 час? в 23 часа 30 мин.?
2) На сколько градусов повернётся часовая стрелка за 2 часа? 5 час? 8 час? 30 мин.?
3) Сколько градусов содержит дуга, равная половине окружности? 1 / 4 окружности? 1 / 24 окружности? 5 / 24 окружности?
576. 1) Начертите с помощью транспортира: а) прямой угол; б) угол в 30°; в) угол в 60°; г) угол в 150°; д) угол в 55°.
2) Измерьте с помощью транспортира углы фигуры и найдите сумму всех углов каждой фигуры (рис. 31).

577.Выполнить действия:

578. 1) Полуокружность разделена на две дуги, из которых одна на 100° больше другой. Найти величину каждой дуги.
2) Полуокружность разделена на две дуги, из которых одна на 15° меньше другой. Найти величину каждой дуги.
3) Полуокружность разделена на две дуги, из которых одна в два раза больше другой. Найти величину каждой дуги.
4) Полуокружность разделена на две дуги, из которых одна в 5 раз меньше другой. Найти величину каждой дуги.
579. 1) На диаграмме «Грамотность населения в СССР» (рис. 32) изображено число грамотных, приходящихся на сто человек населения. По данным диаграммы и её масштабу определить число грамотных мужчин и женщин для каждого из указанных годов.

Результаты записать в таблицу:

2) Используя данные диаграммы «Советские посланцы в Космос» (рис. 33), составить задачи.

580.1) По данным секторной диаграммы «Режим дня для ученика V класса» (рис. 34) заполнить таблицу и ответить на вопросы: какая часть суток отводится на сон? на домашние занятия? на занятия в школе?

2) Построить секторную диаграмму о режиме своего дня.

