Как найти среднюю скорость автомобиля после поездки в разных режимах? Как найти среднюю скорость

Задачи на среднюю скорость (далее СК). Мы уже рассматривали задания на прямолинейное движение. Рекомендую посмотреть статьи " " и " " . Типовые задания на среднюю скорость это группа задач на движение, они включены в ЕГЭ по математике и такая задача вполне вероятно может оказаться перед вами в момент самого экзамена. Задачки простые, решаются быстро.

Смысл таков: представьте объект передвижения, например автомобиль. Он проходит определённые участки пути с разной скоростью. На весь путь затрачивается какое-то определённое время. Так вот: средняя скорость это такая постоянная скорость с которой автомобиль преодолел бы данный весть путь за это же время То есть формула средней скорости такова:

Если участков пути было два, тогда

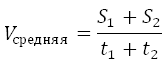
Если три, то соответственно:

*В знаменателе суммируем время, а в числителе расстояния пройденные за соответствующие им отрезки времени.

Первую треть трассы автомобиль ехал со скоростью 90 км/ч, вторую треть – со скоростью 60 км/ч, а последнюю – со скоростью 45 км/ч. Найдите СК автомобиля на протяжении всего пути. Ответ дайте в км/ч.

Как уже сказано необходимо весь путь разделить на всё время движения. В условии сказано о трёх участках пути. Формула:

Обозначим весь пусть S. Тогда первую треть пути автомобиль ехал:

Вторую треть пути автомобиль ехал:

Последнюю треть пути автомобиль ехал:

Таким образом

Решите самостоятельно:

Первую треть трассы автомобиль ехал со скоростью 60 км/ч, вторую треть – со скоростью 120 км/ч, а последнюю – со скоростью 110 км/ч. Найдите СК автомобиля на протяжении всего пути. Ответ дайте в км/ч.

Первый час автомобиль ехал со скоростью 100 км/ч, следующие два часа – со скоростью 90 км/ч, а затем два часа – со скоростью 80 км/ч. Найдите СК автомобиля на протяжении всего пути. Ответ дайте в км/ч.

В условии сказано о трёх участках пути. СК будем искать по формуле:

Участки пути нам не даны, но мы можем без труда их вычислить:

Первый участок пути составил 1∙100 = 100 километров.

Второй участок пути составил 2∙90 = 180 километров.

Третий участок пути составил 2∙80 = 160 километров.

Вычисляем скорость:

Решите самостоятельно:

Первые два часа автомобиль ехал со скоростью 50 км/ч, следующий час – со скоростью 100 км/ч, а затем два часа – со скоростью 75 км/ч. Найдите СК автомобиля на протяжении всего пути. Ответ дайте в км/ч.

Первые 120 км автомобиль ехал со скоростью 60 км/ч, следующие 120 км - со скоростью 80 км/ч, а затем 150 км - со скоростью 100 км/ч. Найдите СК автомобиля на протяжении всего пути. Ответ дайте в км/ч.

Сказано о трёх участках пути. Формула:

Протяжённость участков дана. Определим время, которое автомобиль затратил на каждый участок: на первый затрачено 120/60 часов, на второй участок 120/80 часов, на третий 150/100 часов. Вычисляем скорость:

Решите самостоятельно:

Первые 190 км автомобиль ехал со скоростью 50 км/ч, следующие 180 км - со скоростью 90 км/ч, а затем 170 км - со скоростью 100 км/ч. Найдите СК автомобиля на протяжении всего пути. Ответ дайте в км/ч.

Половину времени, затраченного на дорогу, автомобиль ехал со скоростью 74 км/ч, а вторую половину времени – со скоростью 66 км/ч. Найдите СК автомобиля на протяжении всего пути. Ответ дайте в км/ч.

*Есть задача про путешественника, который пересёк море. С решением у ребят возникают проблемы. Если вы не видите его, то пройдите регистрацию на сайте! Кнопка регистрации (входа) находится в ГЛАВНОМ МЕНЮ сайта. После регистрации войдите на сайт и обновите данную страницу.

Путешественник переплыл море на яхте со средней скоростью 17 км/ч. Обратно он летел на спортивном самолете со скоростью 323 км/ч. Найдите среднюю скорость путешественника на протяжении всего пути. Ответ дайте в км/ч.

С уважением, Александр.

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

Есть средние величины, неправильное определение которых вошло в анекдот или в притчу. Любые неверно произведённые расчёты комментируются расхожей общепонятной ссылкой на такой заведомо абсурдный результат. У каждого, к примеру, вызовет улыбку саркастического понимания фраза "средняя температура по больнице". Однако те же знатоки нередко, не задумываясь, складывают скорости на отдельных отрезках пути и делят подсчитанную сумму на число этих участков, чтобы получить столь же бессмысленный ответ. Напомним из курса механики средней школы, как найти среднюю скорость правильным, а не абсурдным способом.

Аналог "средней температуры" в механике

В каких случаях каверзно сформулированные условия задачи подталкивают нас к поспешному необдуманному ответу? Если говорится о "частях" пути, но не указывается их протяжённость, это настораживает даже мало искушённого в решении подобных примеров человека. А вот если в задаче прямо указывается на равные промежутки, например, "первую половину пути поезд следовал со скоростью...", или "первую треть пути пешеход прошагал соскоростью...", и далее подробно расписывается, как объёкт передвигался на оставшихся равных участках, то есть известно соотношение S 1 = S 2 = ... = S n и точные значения скоростей v 1, v 2, ... v n , наше мышление нередко даёт непростительную осечку. Считается среднее арифметическое скоростей, то есть все известные значения v складываются и делятся на n . В итоге ответ получается неверный.

Простые "формулы" расчёта величин при равномерном движении

И для всего пройденного пути, и для отдельных его участков в случае усреднения скорости справедливы соотношения, написанные для равномерного движения :

• S = vt (1), "формула" пути;
• t=S/v (2), "формула" расчёта времени движения;
• v=S/t (3), "формула" определения средней скорости на участке пути S , пройденном за время t .

То есть для нахождения искомой величины v с использованием соотношения (3) нам нужно точно знать две другие. Именно решая вопрос, как найти среднюю скорость движения, мы прежде всего должны определить, каков весь пройденный путь S и каково всё время движения t .

Математическое обнаружение скрытой ошибки

В решаемом нами примере пройденный телом (поездом или пешеходом) путь будет равен произведению nS n (так как мы n раз складываем равные участки пути, в приведённых примерах - половинки, n = 2 , или трети, n = 3 ). О полном же времени движения нам ничего не известно. Как определить среднюю скорость, если знаменатель дроби (3) явно не задан? Воспользуемся соотношением (2), для каждого участка пути определим t n = S n: v n . Сумму рассчитанных таким образом промежутков времени запишем под чертой дроби (3). Ясно, что, для того чтобы избавиться от знаков "+", нужно приводить все S n: v n к общему знаменателю. В результате получается "двухэтажная дробь". Далее пользуемся правилом: знаменатель знаменателя идёт в числитель. В итоге, для задачи с поездом после сокращения на S n имеем v ср = nv 1 v 2: v 1 + v 2 , n = 2 (4) . Для случая с пешеходом вопрос -, как найти среднюю скорость, решается ещё сложнее: v ср = nv 1 v 2 v 3: v 1v2 + v 2 v 3 + v 3 v 1 , n = 3 (5).

Явное подтверждение ошибки "в числах"

Для того чтобы "на пальцах" подтвердить, что определение среднего арифметического - ошибочный путь при расчёте v ср , конкретизируем пример, заменив абстрактные буквы числами. Для поезда возьмём скорости 40 км/ч и 60 км/ч (ошибочный ответ - 50 км/ч ). Для пешехода - 5 , 6 и 4 км/ч (среднее арифметическое - 5 км/ч ). Нетрудно убедиться, подставив значения в соотношения (4) и (5), что верными ответами будут для локомотива 48 км/ч и для человека - 4,(864) км/ч (периодическая десятичная дробь, результат математически не слишком красивый).

Когда среднее арифметическое "не подводит"

Если задача формулируется так: "За равные промежутки времени тело двигалось сначала со скоростью v 1 , затем v 2 , v 3 и так далее", быстрый ответ на вопрос, как найти среднюю скорость, может быть найден неправильным способом. Предоставим читателю самостоятельно в этом убедиться, просуммировав в знаменателе равные промежутки времени и воспользовавшись в числителе v ср соотношением (1). Это, пожалуй, единственный случай, когда ошибочный метод приводит к получению корректного результата. Но для гарантированно точных расчётов нужно пользоваться единственно правильным алгоритмом, неизменно обращаясь к дроби v ср = S: t .

Алгоритм на все случаи жизни

Для того чтобы наверняка избежать ошибки, при решении вопроса, как найти среднюю скорость, достаточно запомнить и выполнить простую последовательность действий:

• определить весь путь, просуммировав длины отдельных его участков;
• установить всё время пути;
• поделить первый результат на второй, неизвестные, не заданные в задаче величины при этом (при условии корректной формулировки условий) сокращаются.

В статье рассмотрены простейшие случаи, когда исходные данные приводятся для равных долей времени или равных участков пути. В общем случае соотношение хронологических промежутков либо пройденных телом расстояний может быть самым произвольным (но при этом математически определённым, выраженным конкретным целым числом или дробью). Правило обращения к соотношению v ср = S: t абсолютно универсально и никогда не подводит, сколь бы сложные на первый взгляд алгебраические преобразования ни приходилось выполнять.

Напоследок отметим: для наблюдательных читателей не осталась незамеченной практическая значимость использования верного алгоритма. Правильно рассчитанная средняя скорость в приведённых примерах оказалась несколько ниже "средней температуры" на трассе. Поэтому ложный алгоритм для систем, фиксирующих превышения скорости, означал бы большее число ошибочных постановлений ГИБДД, высылаемых в "письмах счастья" водителям.

Очень просто! Нужно весь путь разделить на время, которое объект движения находился в пути. Выражаясь иначе, можно определить среднюю скорость как среднее арифметическое всех скоростей движения объекта. Но существуют некоторые нюансы при решении задач данного направления.

Например, для вычисления средней скорости даётся такой вариант задачи: путник сначала шёл со скоростью 4 км в час в течение часа. Затем попутная машина «подобрала» его, и остаток пути он проехал за 15 минут. Причём автомобиль шёл со скоростью 60 км в час. Как определить среднюю скорость перемещения путника?

Не следует просто складывать 4 км и 60 и делить их пополам, это будет неверный ход решения! Ведь пройденные пути пешком и на автомашине нам неизвестны. Значит, сначала нужно вычислить весь путь.

Первую часть пути найти легко: 4 км в час Х 1 час = 4 км

Со второй частью пути небольшие проблемы: скорость выражена в часах, а время движения - в минутах. Этот нюанс частенько мешает найти правильный ответ, когда поставлены вопросы, как найти среднюю скорость, путь или время.

Выразим 15 минут в часах. Для этого 15 мин: 60 мин = 0,25 часа. Теперь рассчитаем, какой же путь путник проделал на попутке?

60 км/ ч Х 0,25ч = 15 км

Теперь найти весь преодолённый путником путь не составит особого труда: 15 км + 4 км = 19 км.

Время движения также довольно легко вычислить. Это 1 час + 0,25 часа = 1,25 часа.

И теперь уже понятно, как найти среднюю скорость: нужно весь путь поделить на время, которое путник затратил на его преодоление. То есть, 19 км: 1,25 часа = 15,2 км/час.

Есть такой анекдот в тему. Мужчина, торопящийся на спрашивает владельца поля: «Можно ли мне пройти к вокзалу через ваш участок? Я немного опаздываю и хотел бы сократить свой путь, пройдя напрямую. Тогда я определённо успею к электричке, которая отходит в 16 часов 45 минут!» - «Конечно, вы можете сократить свой путь, пройдя через мой луг! И если вас там заметит мой бык, то вы успеете даже на ту электричку, которая отходит в 16 часов 15 минут».

Эта комичная ситуация, между тем, имеет самое прямое отношение к такому математическому понятию, как средняя скорость движения. Ведь потенциальный пассажир пытается сократить свой путь по той простой причине, что он знает среднюю скорость своего движения, например, 5 км в час. И пешеход, зная, что обходной путь по асфальтированной дороге равняется 7,5 км, произведя мысленно простые вычисления, понимает, что ему потребуется на эту дорогу полтора часа (7,5 км: 5 км/час = 1,5 час).

Он же, выйдя из дома слишком поздно, ограничен во времени, поэтому и решает сократить свой путь.

И вот тут мы сталкиваемся с первым правилом, которое диктует нам, как найти среднюю скорость движения: учитывая прямое расстояние между крайними точками пути или именно просчитывая Из вышесказанного всем ясно: следует вести расчёт, принимая во внимание именно траекторию пути.

Сократив путь, но не изменяя свою среднюю скорость, объект в лице пешехода получает выигрыш во времени. Фермер же, предполагая среднюю скорость убегающего от разъярённого быка «спринтера», также делает простые расчёты и выдаёт свой результат.

Автомобилисты часто используют второе, немаловажное, правило вычисления средней скорости, которое касается времени нахождения в пути. Это касается того вопроса, как найти среднюю скорость в случае, если объект имеет во время пути остановки.

В этом варианте обычно, если нет дополнительных уточнений, для расчёта берут полное время, включая остановки. Поэтому водитель авто может сказать, что его средняя скорость движения утром по свободной дороге намного выше, чем средняя скорость движения в час-пик, хотя спидометр показывает одну и ту же цифру в обоих вариантах.

Зная эти цифры, опытный шофёр никогда и никуда не опоздает, заранее предположив, какова будет его средняя скорость передвижения в городе в разное время суток.

2 . Первый участок длиной 120 м лыжник прошел за 2 мин, а второй длиной 27 м он прошел за 1,5 мин. Найдите среднюю скорость движения лыжника на всем пути.

3 . Двигаясь по шоссе, велосипедист проехал 20 км за 40 мин, затем проселочную дорогу длиной 600 м он преодолел за 2 мин, а оставшиеся 39 км 400 м по шоссе он проехал за 78 мин. Чему равна средняя скорость на всем пути?

4 . Мальчик за 25 мин прошел 1,2 км, затем полчаса отдыхал, а затем пробежал еще 800 м за 5 мин. Какова была его средняя скорость на всем пути?

Уровень B

1 . О какой скорости – средней или мгновенной – идет речь в следующих случаях:

а) пуля вылетает из винтовки со скоростью 800 м/с;

б) скорость движения Земли вокруг Солнца 30 км/с;

в) на участке дороги установлен ограничитель максимальной скорости – 60 км/ч;

г) мимо вас проехал автомобиль со скоростью 72 км/ч;

д) автобус преодолел расстояние между Могилевом и Минском со скоростью 50 км/ч?

2 . Путь в 63 км от одной станции до другой электропоезд проходит за 1 ч 10 мин со средней скоростью 70 км/ч. Какое время занимают остановки?

3 . Самоходная косилка имеет ширину захвата 10 м. Определите площадь поля, скошенного за 10 мин, если средняя скорость косилки 0,1 м/с.

4 . На горизонтальном участке пути автомобиль ехал со скоростью 72 км/ч в течение 10 мин, а затем проехал подъем со скоростью 36 км/ч за 20 мин. Чему равна средняя скорость на всем пути?

5 . Велосипедист первую половину времени при переезде из одного пункта в другой ехал со скоростью 12 км/ч, а вторую половину времени (из-за прокола шины) шел пешком со скоростью 4 км/ч. Определите среднюю скорость движения велосипедиста.

6 . Школьник проехал 1/3 всего времени на автобусе со скоростью 60 км/ч, еще 1/3 всего времени на велосипеде со скоростью 20 км/ч, остальное время прошел со скоростью 7 км/ч. Определите среднюю скорость движения школьника.

7 . Велосипедист ехал из одного города в другой. Половину пути он проехал со скоростью 12 км/ч, а вторую половину (из-за прокола шины) шел пешком со скоростью 4 км/ч. Определите среднюю скорость его движения.

8 . Из одного пункта в другой мотоциклист двигался со скоростью 60 км/ч, обратный путь им был пройден со скоростью 10 м/с. Определите среднюю скорость мотоциклиста за все время движения.

9 . Школьник проехал 1/3 пути на автобусе со скоростью 40 км/ч, еще 1/3 пути на велосипеде со скоростью 20 км/ч, последнюю треть пути прошел со скоростью 10 км/ч. Определите среднюю скорость движения школьника.

10 . Пешеход часть пути прошел со скоростью 3 км/ч, затратив на это 2/3 времени своего движения. Оставшееся время он прошел со скоростью 6 км/ч. Определите среднюю скорость.

11 . Скорость поезда на подъеме 30 км/ч, а на спуске – 90 км/ч. Определите среднюю скорость на вcем участке пути, если спуск в два раза длиннее подъема.

12 . Половину времени при переезде из одного пункта в другой автомобиль двигался с постоянной скоростью 60 км/ч. С какой постоянной скоростью он должен двигаться оставшееся время, если средняя скорость движения равна 65 км/ч?

В данной статье рассказано о том, как найти среднюю скорость. Дано определение этого понятия, а также рассмотрено два важных частных случая нахождения средней скорости. Представлен подробный разбор задач на нахождение средней скорости тела от репетитора по математике и физике.

Определение средней скорости

Средней скоростью движения тела называется отношение пути , пройденного телом, ко времени , в течение которого двигалось тело:

Научимся ее находить на примере следующей задачи:

Обратите внимание, что в данном случае это значение не совпало со средним арифметическим скоростей и , которое равно:
м/с.

Частные случаи нахождения средней скорости

1. Два одинаковых участка пути. Пусть первую половину пути тело двигалось со скоростью , а вторую половину пути — со скоростью . Требуется найти среднюю скорость движения тела.

2. Два одинаковых интервала движения. Пусть тело двигалось со скоростью в течение некоторого промежутка времени, а затем стало двигаться со скоростью в течение такого же промежутка времени. Требуется найти среднюю скорость движения тела.

Здесь мы получили единственный случай, когда средняя скорость движения совпала со средним арифметическим скоростей и на двух участках пути.

Решим напоследок задачу из Всероссийской олимпиады школьников по физике, прошедшей в прошлом году, которая связана с темой нашего сегодняшнего занятия.

Пройденный телом путь составляет: м. Можно найти также путь, который прошло тело за последние с своего движения: м. Тогда за первые с своего движения тело преодолело путь в м. Следовательно, средняя скорость на этом участке пути составила:
м/с.

Задачи на нахождение средней скорости движения очень любят предлагать на ЕГЭ и ОГЭ по физике, вступительных экзаменах, а также олимпиадах. Научиться решать эти задачи должен каждый школьник, если он планирует продолжить свое обучение в вузе. Помочь справиться с этой задачей может знающий товарищ, школьный учитель или репетитор по математике и физике. Удачи вам в изучении физики!

Сергей Валерьевич