Desigualdades logarítmicas y sus soluciones. Resolver sistemas de desigualdades logarítmicas y exponenciales con un tutor

Definición de logaritmo La forma más sencilla de escribirlo matemáticamente es:

La definición de logaritmo se puede escribir de otra forma:

Preste atención a las restricciones que se imponen sobre la base del logaritmo ( a) y a la expresión sublogarítmica ( X). En el futuro, estas condiciones se convertirán en restricciones importantes para OD, que deberán tenerse en cuenta a la hora de resolver cualquier ecuación con logaritmos. Entonces, ahora, además de las condiciones estándar que conducen a restricciones en ODZ (positividad de las expresiones bajo las raíces de potencias pares, denominador diferente a cero, etc.), también se deben tener en cuenta las siguientes condiciones:

• La expresión sublogarítmica solo puede ser positiva.
• La base del logaritmo solo puede ser positiva y no igual a uno..

Tenga en cuenta que ni la base del logaritmo ni la expresión sublogarítmica pueden ser iguales a cero. Tenga en cuenta también que el valor del logaritmo en sí puede tomar todos los valores posibles, es decir El logaritmo puede ser positivo, negativo o cero. Los logaritmos tienen muchas propiedades diferentes que se derivan de las propiedades de las potencias y de la definición de logaritmo. Enumerémoslos. Entonces, las propiedades de los logaritmos:

Logaritmo del producto:

Logaritmo de una fracción:

Sacando el grado del signo del logaritmo:

Preste especial atención a aquellas de las últimas propiedades enumeradas en las que aparece el signo del módulo después de tomar el grado. No olvides que al colocar una potencia par fuera del signo del logaritmo, debajo del logaritmo o en la base, debes dejar el signo del módulo.

Otro características beneficiosas logaritmos:

La última propiedad se utiliza muy a menudo en ecuaciones y desigualdades logarítmicas complejas. Debe ser recordado tan bien como todos los demás, aunque a menudo se le olvide.

Las ecuaciones logarítmicas más simples son:

Y su solución viene dada por una fórmula que se deriva directamente de la definición del logaritmo:

Otras ecuaciones logarítmicas más simples son aquellas que, utilizando transformaciones algebraicas y las fórmulas y propiedades de los logaritmos anteriores, se pueden reducir a la forma:

La solución a tales ecuaciones teniendo en cuenta la ODZ es la siguiente:

Algunos otros ecuaciones logarítmicas con una variable en la base se puede reducir a la forma:

En tales ecuaciones logarítmicas forma general la solución también se deriva directamente de la definición del logaritmo. Sólo en este caso existen restricciones adicionales para DZ que deben tenerse en cuenta. Como resultado, para resolver una ecuación logarítmica con una variable en la base, necesitas resolver el siguiente sistema:

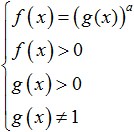
Al resolver ecuaciones logarítmicas más complejas que no se pueden reducir a una de las ecuaciones presentadas anteriormente, también se utiliza activamente. método de reemplazo de variables. Como de costumbre, al utilizar este método, es necesario recordar que después de introducir el reemplazo, la ecuación debe simplificarse y ya no contener la antigua incógnita. También debe recordar realizar la sustitución inversa de variables.

A veces, al resolver ecuaciones logarítmicas también hay que utilizar método gráfico . Este método consiste en construir gráficas de funciones que están en los lados izquierdo y derecho de la ecuación con la mayor precisión posible en un plano de coordenadas y luego encontrar las coordenadas de sus puntos de intersección en el dibujo. Las raíces obtenidas de esta manera deben verificarse mediante sustitución en la ecuación original.

A la hora de resolver ecuaciones logarítmicas también suele ser útil método de agrupación. Al utilizar este método, lo principal a recordar es que: para que el producto de varios factores sea igual a cero, es necesario que al menos uno de ellos sea igual a cero, y el resto existió. Cuando los factores son logaritmos o paréntesis con logaritmos, y no solo paréntesis con variables como en ecuaciones racionales, entonces pueden ocurrir muchos errores. Dado que los logaritmos tienen muchas restricciones en la región donde existen.

Al decidir sistemas de ecuaciones logarítmicas la mayoría de las veces hay que utilizar el método de sustitución o el método de sustitución de variables. Si existe tal posibilidad, entonces al resolver sistemas de ecuaciones logarítmicas, uno debe esforzarse por garantizar que cada una de las ecuaciones del sistema se lleve individualmente a una forma en la que sea posible hacer la transición de una ecuación logarítmica a una uno racional.

Protozoos desigualdades logarítmicas se resuelven aproximadamente de la misma manera que ecuaciones similares. Primero, usando transformaciones algebraicas y las propiedades de los logaritmos, debemos intentar llevarlos a una forma en la que los logaritmos en los lados izquierdo y derecho de la desigualdad tengan las mismas bases, es decir, obtenga una desigualdad de la forma:

Después de lo cual es necesario pasar a una desigualdad racional, teniendo en cuenta que esta transición debe realizarse de la siguiente manera: si la base del logaritmo es mayor que uno, entonces no es necesario cambiar el signo de la desigualdad, y si la la base del logaritmo es menor que uno, entonces debes cambiar el signo de la desigualdad al opuesto (esto significa cambiar "menos" por "más" o viceversa). En este caso, no es necesario cambiar los signos menos a más, sin pasar por las reglas aprendidas previamente. Anotemos matemáticamente lo que obtenemos como resultado de realizar dicha transición. Si la base es mayor que uno obtenemos:

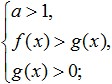
Si la base del logaritmo es menor que uno, cambiamos el signo de la desigualdad y obtenemos el siguiente sistema:

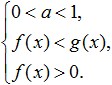
Como vemos, al resolver desigualdades logarítmicas, como es habitual, también se tiene en cuenta la ODZ (esta es la tercera condición en los sistemas anteriores). Además, en este caso es posible no exigir la positividad de ambas expresiones sublogarítmicas, sino sólo la positividad de la menor de ellas.

Al decidir desigualdades logarítmicas con una variable en la base logaritmo, es necesario considerar ambas opciones de forma independiente (cuando la base es menor que uno y mayor que uno) y combinar las soluciones de estos casos en un conjunto. Al mismo tiempo, no debemos olvidarnos de la DL, es decir. sobre el hecho de que tanto la base como todas las expresiones sublogarítmicas deben ser positivas. Así, al resolver una desigualdad de la forma:

Obtenemos el siguiente conjunto de sistemas:

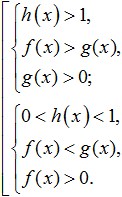
Las desigualdades logarítmicas más complejas también se pueden resolver mediante cambios de variables. Algunas otras desigualdades logarítmicas (así como ecuaciones logarítmicas) requieren el procedimiento de tomar el logaritmo de ambos lados de la desigualdad o ecuación a resolver. misma base. Entonces, al realizar un procedimiento de este tipo con desigualdades logarítmicas, hay una sutileza. Tenga en cuenta que al llevar logaritmos a una base mayor que uno, el signo de desigualdad no cambia, pero si la base es menor que uno, entonces el signo de desigualdad se invierte.

Si una desigualdad logarítmica no se puede reducir a racional o resolver mediante una sustitución, entonces en este caso se debe usar método de intervalo generalizado, que es el siguiente:

• Definir licencia de conducir;
• Transformar la desigualdad para que quede un cero en el lado derecho (en el lado izquierdo, si es posible, reducir a un denominador común, factorizar, etc.);
• Encuentra todas las raíces del numerador y denominador y trácalas en el eje numérico, y si la desigualdad no es estricta, pinta sobre las raíces del numerador, pero en cualquier caso deja las raíces del denominador punteadas;
• Encuentra el signo de la expresión completa en cada uno de los intervalos sustituyendo un número de un intervalo dado en la desigualdad transformada. En este caso, ya no es posible alternar signos de ningún modo al pasar por puntos del eje. Es necesario determinar el signo de una expresión en cada intervalo sustituyendo el valor del intervalo en esta expresión, y así sucesivamente para cada intervalo. Esto ya no es posible (ésta es, en general, la diferencia entre el método de intervalo generalizado y el habitual);
• Encuentre la intersección de la ODZ y los intervalos que satisfacen la desigualdad, pero no pierda los puntos individuales que satisfacen la desigualdad (las raíces del numerador en desigualdades no estrictas), y no olvide excluir de la respuesta todas las raíces de la denominador en todas las desigualdades.

• Atrás
• Adelante

¿Cómo prepararse con éxito para el CT en física y matemáticas?

Para prepararse con éxito para el CT en física y matemáticas, es necesario, entre otras cosas, cumplir tres condiciones fundamentales:

1. Estudie todos los temas y complete todas las pruebas y tareas proporcionadas en los materiales educativos de este sitio. Para hacer esto, no necesita nada en absoluto, a saber: dedicar de tres a cuatro horas todos los días a prepararse para el CT en física y matemáticas, estudiar teoría y resolver problemas. El caso es que el CT es un examen donde no basta solo con saber física o matemáticas, también hay que saber resolver rápido y sin fallos. un gran número de tareas para diferentes temas y de diversa complejidad. Esto último sólo se puede aprender resolviendo miles de problemas.
2. Aprenda todas las fórmulas y leyes de la física, y fórmulas y métodos de las matemáticas. De hecho, esto también es muy sencillo de hacer; en física sólo hay unas 200 fórmulas necesarias, y en matemáticas incluso un poco menos. Cada uno de estos artículos contiene alrededor de una docena. métodos estándar resolver problemas de un nivel básico de complejidad, que además se pueden aprender, y así, de forma totalmente automática y sin dificultad, resolver la mayor parte de los CT en el momento adecuado. Después de esto, sólo tendrás que pensar en las tareas más difíciles.
3. Asista a las tres etapas de las pruebas de ensayo en física y matemáticas. Cada RT se puede visitar dos veces para decidirse por ambas opciones. Nuevamente, en el CT, además de la capacidad de resolver problemas de manera rápida y eficiente y el conocimiento de fórmulas y métodos, también debe poder planificar adecuadamente el tiempo, distribuir fuerzas y, lo más importante, completar correctamente el formulario de respuesta, sin confundiendo los números de respuestas y problemas, o su propio apellido. Además, durante la RT, es importante acostumbrarse al estilo de hacer preguntas en los problemas, lo que puede parecer muy inusual para una persona no preparada en el DT.

La implementación exitosa, diligente y responsable de estos tres puntos te permitirá mostrar un excelente resultado en el CT, el máximo de lo que eres capaz de hacer.

¿Encontraste un error?

Si cree que ha encontrado un error en los materiales de formación, escríbalo por correo electrónico. También puede informar un error a red social(). En la carta indique la materia (física o matemáticas), el nombre o número del tema o prueba, el número del problema o el lugar del texto (página) donde, en su opinión, hay un error. Describa también cuál es el error sospechoso. Su carta no pasará desapercibida, se corregirá el error o se le explicará por qué no es un error.

Una desigualdad se llama logarítmica si contiene función logarítmica.

Los métodos para resolver desigualdades logarítmicas no son diferentes, excepto por dos cosas.

En primer lugar, al pasar de la desigualdad logarítmica a la desigualdad de funciones sublogarítmicas, se debe seguir el signo de la desigualdad resultante. Obedece la siguiente regla.

Si la base de la función logarítmica es mayor que $1$, entonces al pasar de la desigualdad logarítmica a la desigualdad de funciones sublogarítmicas, el signo de la desigualdad se conserva, pero si es menor que $1$, entonces cambia al opuesto .

En segundo lugar, la solución a cualquier desigualdad es un intervalo y, por lo tanto, al final de resolver la desigualdad de funciones sublogarítmicas es necesario crear un sistema de dos desigualdades: la primera desigualdad de este sistema será la desigualdad de funciones sublogarítmicas, y el segundo será el intervalo del dominio de definición de las funciones logarítmicas incluidas en la desigualdad logarítmica.

Práctica.

Resolvamos las desigualdades:

1. $\log_(2)((x+3)) \geq 3.$

$D(y): \x+3>0.$

$x \en (-3;+\infty)$

La base del logaritmo es $2>1$, por lo que el signo no cambia. Usando la definición de logaritmo, obtenemos:

$x+3 \geq 2^(3),$

$x \en )