Статистическая достоверность имеет существенное значение в расчетной практике ФКС. Ранее было отмечено, что из одной и той же генеральной совокупности может быть избрано множество выборок:
Если они подобраны корректно, то их средние показатели и показатели генеральной совокупности незначительно отличаются друг от друга величиной ошибки репрезентативности с учетом принятой надежности;
Если они избираются из разных генеральных совокупностей, различие между ними оказывается существенным. В статистике повсеместно рассматривается сравнение выборок;
Если они отличаются несущественно, непринципиально, незначительно, т. е. фактически принадлежат одной и той же генеральной совокупности, различие между ними называется статистически недостоверным.
Статистически достовернымразличием выборок называется выборка, которая различается значимо и принципиально, т. е. принадлежит разным генеральным совокупностям.
В ФКС оценка статистической достоверности различий выборок означает решение множества практических задач. Например, введение новых методик обучения, программ, комплексов упражнений, тестов, контрольных упражнений связано с их экспериментальной проверкой, которая должна показать, что испытуемая группа принципиально отлична от контрольной. Поэтому применяют специальные статистические методы, называемые критериями статистической достоверности, позволяющие обнаружить наличие или отсутствие статистически достоверного различия между выборками.
Все критерии делятся на две группы: параметрические и непараметрические. Параметрические критерии предусматривают обязательное наличие нормального закона распределения, т.е. имеется в виду обязательное определение основных показателей нормального закона — средней арифметической величины и среднего квадратического отклонения s. Параметрические критерии являются наиболее точными и корректными. Непараметрические критерии основаны на ранговых (порядковых) отличиях между элементами выборок.
Приведем основные критерии статистической достоверности, используемые в практике ФКС: критерий Стьюдента и критерий Фишера.
Критерий Стьюдента назван в честь английского ученого К. Госсета (Стьюдент — псевдоним), открывшего данный метод. Критерий Стьюдента является параметрическим, используется для сравнения абсолютных показателей выборок. Выборки могут быть различными по объему.
Критерий Стьюдента определяется так.
1. Находим критерий Стьюдента t по следующей формуле:
где — средние арифметические сравниваемых выборок; т 1 , т 2 — ошибки репрезентативности, выявленные на основании показателей сравниваемых выборок.
2. Практика в ФКС показала, что для спортивной работы достаточно принять надежность счета Р = 0,95.
Для надежности счета: Р = 0,95 (a = 0,05), при числе степеней свободы
k = n 1 + п 2 — 2 по таблице приложения 4 находим величину граничного значения критерия (t гр).
3. На основании свойств нормального закона распределения в критерии Стьюдента осуществляется сравнение t и t гр.
Делаем выводы:
если t t гр, то различие между сравниваемыми выборками статистически достоверно;
если t t гр, то различие статистически недостоверно.
Для исследователей в области ФКС оценка статистической достоверности является первым шагом в решении конкретной задачи: принципиально или непринципиально различаются между собой сравниваемые выборки. Последующий шаг заключается в оценке этого различия с педагогической точки зрения, что определяется условием задачи.
Рассмотрим применение критерия Стьюдента на конкретном примере.
Пример 2.14. Группа испытуемых в количестве 18 человек оценена на ЧСС (уд./мин) до х i и после y i разминки.
Оценить эффективность разминки по показателю ЧСС. Исходные данные и расчеты представлены в табл. 2.30 и 2.31.
Таблица 2.30
Обработка показателей ЧСС до разминки
Ошибки по обеим группам совпали, так как объемы выборок равны (исследуется одна и та же группа при различных условиях), а средние квадратические отклонения составили s х = s у = 3 уд./мин. Переходим к определению критерия Стьюдента:
Задаем надежность счета: Р= 0,95.
Число степеней свободы k 1 = n 1 + п 2 — 2=18+18-2 = 34. По таблице приложения 4 находим t гр= 2,02.
Статистический вывод. Поскольку t = 11,62, а граничное t гр = 2,02, то 11,62 > 2,02, т.е. t > t гр, поэтому различие между выборками статистически достоверно.
Педагогический вывод. Установлено, что по показателю ЧСС различие между состоянием группы до и после разминки является статистически достоверным, т.е. значимым, принципиальным. Итак, по показателю ЧСС можно сделать вывод, что разминка эффективна.
Критерий Фишера является параметрическим. Он применяется при сравнении показателей рассеивания выборок. Это, как правило, означает сравнение по показателям стабильности спортивной работы или стабильности функциональных и технических показателей в практике физической культуры и спорта. Выборки могут быть разновеликими.
Критерий Фишера определяется в нижеприведенной последовательности.
1. Находим Критерий Фишера F по формуле
где , — дисперсии сравниваемых выборок.
Условиями критерия Фишера предусмотрено, что в числителе формулы F находится большая дисперсия, т.е. число F всегда больше единицы.
Задаем надежность счета: Р = 0,95 — и определяем числа степеней свободы для обеих выборок: k 1 = n 1 — 1 , k 2 = п 2 — 1.
По таблице приложения 4 находим граничное значение критерия F гр.
Сравнение критериев F и F грпозволяет сформулировать выводы:
если F > F гр, то различие между выборками статистически достоверно;
если F
Приведем конкретный пример.
Пример 2.15. Проанализируем две группы гандболистов: х i (n 1 = 16 человек) и y i (п 2 = 18 человек). Эти группы спортсменов исследованы на время отталкивания (с) при броске мяча в ворота.
Однотипны ли показатели отталкивания?
Исходные данные и основные расчеты представлены в табл. 2.32 и 2.33.
Таблица 2.32
Обработка показателей отталкивания первой группы гандболистов
Определим критерий Фишера:
По данным, представленным в таблице приложения 6, находим Fгр: Fгр = 2,4
Обратим внимание на то, что в таблице приложения 6 перечисление чисел степеней свободы как большей, так и меньшей дисперсии при приближении к большим числам становится грубее. Так, числа степеней свободы большей дисперсии следует в таком порядке: 8, 9, 10, 11, 12, 14, 16, 20, 24 и т.д., а меньшей — 28, 29, 30, 40, 50 и т.д.
Это объясняется тем, что при увеличении объема выборок различия F-критерия уменьшаются и можно использовать табличные значения, приближенные к исходным данным. Так, в примере 2.15 =17 отсутствует и можно принять ближайшее к нему значение k = 16, откуда и получаем Fгр = 2,4.
Статистический вывод. Поскольку критерий Фишера F= 2,5 > F= 2,4, выборки различимы статистически достоверно.
Педагогический вывод. Значения времени отталкивания (с) при броске мяча в ворота у гандболистов обеих групп существенно различаются. Эти группы следует рассматривать как различные.
Дальнейшие исследования должны показать, в чем причина такого различия.
Пример 2.20.(на статистическую достоверность выборки). Повысилась ли квалификация футболиста, если время (с) от подачи сигнала до удара по мячу ногой в начале тренировки было x i , а в конце у i .
Исходные данные и основные расчеты приведены в табл. 2.40 и 2.41.
Таблица 2.40
Обработка показателей времени от подачи сигнала до удара по мячу в начале тренировки
Определим различие групп показателей по критерию Стьюдента:
![]()
При надежности Р = 0,95 и степенях свободы k = n 1 + п 2 — 2 = 22 + 22 — 2 = 42 по таблице приложения 4 находим t гр= 2,02. Поскольку t = 8,3 > t гр= 2,02 — различие статистически достоверно.
Определим различие групп показателей по критерию Фишера:
![]()
По таблице приложения 2 при надежности Р = 0,95 и степенях свободы k = 22-1=21 значение F гр = 21. Поскольку F= 1,53
Статистический вывод. По среднему арифметическому показателю различие групп показателей статистически достоверно. По показателю рассеивания (дисперсии) различие групп показателей статистически недостоверно.
Педагогический вывод.Квалификация футболиста существенно повысилась, однако следует уделить внимание стабильности его показаний.
Подготовка к работе
Перед проведением данной лабораторной работы по дисциплине «Спортивная метрология» всем студентам учебной группы необходимо сформировать рабочие бригады по 3-4 студента в каждой, для совместного выполнения рабочего задания всех лабораторных работ.
При подготовке к работе ознакомиться с соответствующими разделами рекомендуемой литературы (см.раздел 6 данных методических указаний) и конспектов лекций. Изучить разделы 1 и 2 на данную лабораторную работу, а также рабочее задание на неё (раздел 4).
Заготовить форму отчета на стандартных листах писчей бумаги формата А4 и занести в нее материалы необходимые для работы.
Отчет должен содержать:
Титульный лист с указанием кафедры (УК и ТР), учебной группы, фамилии, имени, отчества студента, номера и названия лабораторной работы, даты ее выполнения, а также фамилии, учёной степени, учёного звания и должности преподавателя, принимающего работу;
Цель работы;
Формулы с числовыми значениями, поясняющие промежуточные и окончательные результаты вычислений;
Таблицы измеренных и вычисленных величин;
Требуемый по заданию графический материал;
Краткие выводы по результатам каждого из этапов рабочего задания и в целом по выполненной работе.
Все графики и таблицы вычерчиваются аккуратно при помощи чертежных инструментов. Условные графические и буквенные обозначения должны соответствовать ГОСТам. Допускается оформление отчёта с применением вычислительной (компьютерной) техники.
Рабочее задание
Перед проведением всех измерений каждому члену бригады необходимо изучить правила использования спортивной игры Дартс, приведенные в приложении 7, которые необходимы для проведения нижеприведенных этапов исследований.
I – й этап исследований «Исследование результатов попаданий в мишень спортивной игры Дартс каждым членом бригады на соответствие нормальному закону распределения по критерию χ 2Пирсона и критерию трёх сигм»
1. провести измерение (испытание) своей (личной) быстроты и координированности действий, путём бросания 30-40 раз дротиков в круговую мишень спортивной игры Дартс.
2. Результаты измерений (испытаний) x i (в очках) оформить в виде вариационного ряда и занести в таблицу 4.1 (столбцы , выполнить все необходимые расчёты, заполнить необходимые таблицы и сделать соответствующие выводы на соответствие полученного эмпирического распределения нормальному закону распределения, по аналогии с аналогичными расчётами, таблицами и выводами примера 2.12, приведенного в разделе 2 данных методических указаний на страницах 7 -10.
Таблица 4.1
Соответствие быстроты и координированности действий испытуемых нормальному закону распределения
№ п/п округ- ленно … … Всего
II – й этап исследований
«Оценка средних показателей генеральной совокупности попаданий в мишень спортивной игры Дартс всех студентов учебной группы по результатам измерений членов одной бригады»
Оценить средние показатели быстроты и координированности действий всех студентов учебной группы (согласно списка учебной группы классного журнала) по результатам попаданий в мишень спортивной игры Дартс всех членов бригады, полученным на первом этапе исследований данной лабораторной работы.
1. Оформить результаты измерений быстроты и координированности действийпри бросании дротиков в круговую мишень спортивной игры Дартс всех членов Вашей бригады (2 – 4 человека), которые представляют собой выборку результатов измерений из генеральной совокупности (результаты измерений всех студентов учебной группы – например, 15 человек), занеся их во второй и третий столбцы таблицы 4.2.
Таблица 4.2
Обработка показателей быстроты и координированности действий
членов бригады
№ п/п … … Всего
В таблице 4.2 под следует понимать, совпавшее среднее количество баллов (см. результаты расчётов по таблице 4.1) членами Вашей бригады ( , полученное на первом этапе исследований. Следует заметить, что, как правило, в таблице 4.2 есть рассчитанное среднее значение результатов измерений полученное одним членом бригады на первом этапе исследований, так как вероятность, того что результаты измерений различными членами бригады совпадут очень мала. Тогда, как правило, значения в столбце таблицы 4.2 для каждой из строк — равны 1,а в строке «Всего» графы « », записывается число членов Вашей бригады.
2. Выполнить все необходимые расчёты по заполнению таблицы 4.2, а также другие расчёты и выводы, аналогичные расчётам и выводам примера 2.13, приведенным в 2-ом разделе данной методической разработки на страницах 13-14. Следует иметь ввиду, при расчёте ошибки репрезентативности «m» необходимо использовать формулу 2.4, приведенную на странице 13 данной методической разработки, так как выборка мала (n , а число элементов генеральной совокупности N известно, и равно числу студентов учебной группы, согласно списка журнала учебной группы.
III – й этап исследований
Оценка эффективности разминки по показателю «Быстрота и координированность действий» каждым членом бригады с помощью критерия Стьюдента
Оценить эффективность разминки по бросанию дротиков в мишень спортивной игры «Дартс», выполненную на первом этапе исследований данной лабораторной работы, каждым членом бригады по показателю «Быстрота и координированность действий», с помощью критерия Стьюдента — параметрического критерия статистической достоверности эмпирического закона распределения нормальному закону распределения.
… Всего
2. дисперсии и СКО , результатов измерений показателя «Быстрота и координированность действий» по результатам разминки, приведенных в таблице 4.3, (см. аналогичные расчёты приведенные сразу после таблицы 2.30 примера 2.14 на странице 16 данной методической разработки).
3. Каждому члену рабочей бригады провести измерение (испытание) своей (личной) быстроты и координированности действий после разминки,
… Всего
5. Произвести вычисления среднего значения дисперсии и СКО , результатов измерений показателя «Быстрота и координированность действий» после разминки, приведенных в таблице 4.4, записать в целом результат измерений по результатам разминки(см. аналогичные расчеты, приведенные сразу после таблицы 2.31 примера 2.14 на странице 17 данной методической разработки).
6. Выполнить все необходимые расчёты и выводы, аналогичные расчётам и выводам примера 2.14, приведенным в 2-ом разделе данной методической разработки на страницах 16-17. Следует иметь ввиду, при расчёте ошибки репрезентативности «m» необходимо использовать формулу 2.1, приведенную на странице 12 данной методической разработки, так как выборка n , а число элементов генеральной совокупности N ( неизвестно.
IV – й этап исследований
Оценка однотипности (стабильности) показателей «Быстрота и координированность действий» двух членов бригады с помощью критерия Фишера
Оценить однотипность (стабильность) показателей «Быстрота и координированность действий» двух членов бригады с помощью критерия Фишера, по результатам измерений, полученным на третьем этапе исследований данной лабораторной работы.
Для этого необходимо выполнить следующее.
Используя данные таблиц 4.3 и 4.4, результаты расчётов дисперсий по этим таблицам , полученные на третьем этапе исследований, а также методику расчёта и применения критерия Фишера для оценки однотипности (стабильности) спортивных показателей, приведенную в примере 2.15 на страницах 18-19 данной методической разработки, сделать соответствующие статистический и педагогический выводы.
V – й этап исследований
Оценка групп показателей «Быстрота и координированность действий» одного члена бригады до и после разминки
Уровеньзначимости— это вероятность того, что мы сочлиразличиясущественными, а они на самом делеслучайны.
Когдамы указываем, что различия достовернына 5%-ом уровне значимости,или при р0,05,то мы имеем виду, что вероятность того,чтоони все-таки недостоверны, составляет0,05.
Когдамы указываем, что различия достовернына 1%-ом уровне значимости,или при р0,01,то мы имеем в виду, что вероятность того,чтоони все-таки недостоверны, составляет0,01.
Еслиперевести все это на более формализованныйязык, то уровеньзначимости — это вероятность отклонениянулевой гипотезы, в то времякак она верна.
Ошибка,состоящаявтой,чтомыотклонилинулевуюгипотезу,вто время как она верна, называетсяошибкой 1 рода.(См.Табл. 1)
Табл.1. Нулевая и альтернативные гипотезы ивозможные состояния проверки.
Вероятностьтакой ошибки обычно обозначается какα.В сущности,мы должны были бы указывать в скобкахне р0,05или р0,01,а α0,05или α0,01.
Есливероятность ошибки — это α,то вероятность правильного решения:1-α. Чем меньше α, тем больше вероятностьправильного решения.
Историческисложилось так, что в психологии принятосчитать низшим уровнем статистическойзначимости 5%-ый уровень (р≤0,05): достаточным– 1%-ый уровень (р≤0,01) и высшим 0,1%-ыйуровень (р≤0,001),поэтому в таблицах критических значенийобычно приводятсязначения критериев, соответствующихуровням статистической значимостир≤0,05 и р≤0,01, иногда — р≤0,001. Для некоторыхкритериев втаблицах указан точный уровень значимостиих разных эмпирических значений.Например, для φ*=1,56 р=О,06.
Дотех пор, однако, пока уровень статистическойзначимости не достигнетр=0,05, мы еще не имеем права отклонитьнулевую гипотезу. Мы будем придерживатьсяследующего правила отклонения гипотезыоб отсутствииразличий (Но) и принятия гипотезы остатистической достоверностиразличий (Н 1).
Правило отклонения Hо и принятия h1
Еслиэмпирическое значение критерия равняетсякритическому значению,соответствующему р≤0,05 или превышаетего, то H 0отклоняется,но мы еще не можем определенно принятьH 1 .
Еслиэмпирическое значение критерия равняетсякритическому значению,соответствующему р≤0,01 или превышаетего, то H 0отклоняетсяипринимается Н 1 .
Исключения:критерийзнаков G,критерий Т Вилкоксона и критерий UМанна-Уитни. Для них устанавливаютсяобратные соотношения.

Рис.4. Пример «оси значимости» для критерияQРозенбаума.
Критическиезначения критерия обозначены как Q о,о5и Q 0,01, эмпирическое значение критерия какQ эмп.Оно заключено в эллипс.
Вправоот критического значения Q 0,01простирается «зона значимости» -сюда попадают эмпирические значения,превышающие Q 0 , 01 и,следовательно, безусловно, значимые.
Влевоот критического значения Q 0,05,простирается «зона незначимости»,- сюда попадают эмпирические значенияQ,которые ниже Q 0,05, и,следовательно, безусловно незначимы.
Мывидим, что Q 0,05 =6;Q 0,01 =9;Q эмп. =8;
Эмпирическоезначение критерия попадает в областьмежду Q 0,05и Q 0,01.Это зона «неопределенности»: мыуже можем отклонить гипотезуо недостоверности различий (Н 0),но еще не можем принять гипотезыоб их достоверности (H 1).
Практически,однако, исследователь может считатьдостоверными ужете различия, которые не попадают в зонунезначимости, заявив, что онидостоверны при р0,05,или указав точный уровень значимостиполученного эмпирического значениякритерия, например: р=0,02. С помощьюстандартных таблиц, которые есть вовсех учебниках по математическим методамэтоможно сделать по отношению к критериямН Крускала-Уоллиса, χ 2 r Фридмана,LПейджа, φ* Фишера.
Уровень статистической значимости иликритические значения критериевопределяются по-разному при проверкенаправленных и ненаправленныхстатистических гипотез.
Принаправленной статистической гипотезеиспользуется одностороннийкритерий, при ненаправленной гипотезе- двусторонний критерий.Двусторонний критерий более строг,поскольку он проверяет различияв обе стороны, и поэтому то эмпирическоезначение критерия, которое ранеесоответствовало уровню значимостир0,05,теперь соответствуетлишь уровню р0,10.
Намне придется всякий раз самостоятельнорешать, использует ли он одностороннийили двухстороннийкритерий. Таблицы критических значенийкритериев подобраны такимобразом, что направленным гипотезамсоответствует односторонний,а ненаправленным — двусторонний критерий,и приведенные значенияудовлетворяют тем требованиям, которыепредъявляются к каждому изних. Исследователю необходимо лишьследить за тем, чтобы его гипотезысовпадали по смыслу и по форме сгипотезами, предлагаемыми в описаниикаждого из критериев.
Приобосновании статистического выводаследует решить вопрос, где же проходитлиния между принятием и отвержениемнулевой гипотезы? В силу наличия вэксперименте случайных влияний этаграница не может быть проведена абсолютноточно. Она базируется на понятии уровнязначимости. Уровнем значимостиназываетсявероятность ошибочного отклонениянулевой гипотезы. Или, иными словами,уровень значимости—это вероятностьошибки первого рода при принятии решения.Для обозначения этой вероятности, какправило, употребляют либо греческуюбукву α, либо латинскую букву р.В дальнейшем мы будемупотреблять букву р.
Историческисложилось так, что в прикладных науках,использующих статистику, и в частностив психологии, считается, что низшимуровнем статистической значимостиявляется уровень р =0,05; достаточным -уровень р=0,01 и высшим уровень р=0,001. Поэтому встатистических таблицах, которыеприводятся в приложении к учебникам постатистике, обычно даются табличныезначения для уровней р=0,05, р=0,01 и р= 0,001. Иногда даютсятабличные значения для уровней р-0,025 и р=0,005.
Величины0,05, 0,01 и 0,001 — это так называемыестандартные уровни статистическойзначимости. При статистическом анализеэкспериментальных данных психолог взависимости от задач и гипотез исследованиядолжен выбрать необходимый уровеньзначимости. Как видим, здесь наибольшаявеличина, или нижняя граница уровнястатистической значимости, равняется0,05 — это означает, что допускается пятьошибок в выборке из ста элементов(случаев, испытуемых) или одна ошибкаиз двадцати элементов (случаев,испытуемых). Считается, что ни шесть, нисемь, ни большее количество раз из стамы ошибиться не можем. Цена таких ошибокбудет слишком велика.
Заметим,что в современных статистических пакетахна ЭВМ используются не стандартныеуровни значимости, а уровни, подсчитываемыенепосредственно в процессе работы ссоответствующим статистическимметодом. Эти уровни, обозначаемые буквойр,могутиметь различное числовое выражение винтервале от 0 до 1, например, р=0,7, р= 0,23 или р= 0,012. Понятно, что впервых двух случаях полученные уровнизначимости слишком велики и говоритьо том, что результат значим нельзя. В тоже время в последнем случае результатызначимы на уровне 12 тысячных. Этодостоверный уровень.
Правилопринятия статистического вывода таково:на основании полученных экспериментальныхданных психолог подсчитывает повыбранному им статистическому методутак называемую эмпирическую статистику,или эмпирическое значение. Эту величинуудобно обозначить как Ч эмп .Затем эмпирическаястатистика Ч эмп сравнивается с двумякритическими величинами, которыесоответствуют уровням значимости в 5%и в 1% для выбранного статистическогометода и которые обозначаются как Ч кр .Величины Ч кр находятся для данногостатистического метода по соответствующимтаблицам, приведенным в приложении клюбому учебнику по статистике. Этивеличины, как правило, всегда различныи их в дальнейшем для удобства можноназвать как Ч кр1 иЧ кр2 .Найденные по таблицамвеличины критических значений Ч кр1 иЧ кр2 удобнопредставлять в следующей стандартнойформе записи:
Подчеркнем,однако, что мы использовали обозначенияЧ эмп и Ч кр как сокращение слова«число». Во всех статистических методахприняты свои символические обозначениявсех этих величин: как подсчитаннойпо соответствующему статистическомуметоду эмпирической величины, так инайденных по соответствующим таблицамкритических величин. Например, приподсчете рангового коэффициентакорреляции Спирмена по таблице критическихзначений этого коэффициента были найденыследующие величины критическихзначений, которые для этого методаобозначаются греческой буквой ρ («ро»).Так для р =0,05по таблице найдена величина ρ кр 1= 0,61 и для р =0,01величина ρ кр 2= 0,76.
Впринятой в дальнейшем изложениистандартной форме записи это выглядитследующим образом:

Теперьнам необходимо сравнить наше эмпирическоезначение с двумя найденными потаблицам критическими значениями.Лучше всего это сделать, расположив всетри числа на так называемой «осизначимости». «Ось значимости» представляетсобой прямую, на левом конце которойрасполагается 0, хотя он, как правило,не отмечается на самой этой прямой, ислева направо идет увеличение числовогоряда. По сути дела это привычнаяшкольная ось абсцисс ОХдекартовой системыкоординат. Однако особенность этой осив том, что на ней выделено три участка,«зоны». Одна крайняя зона называетсязоной незначимости, вторая крайняя зона- зоной значимости, а промежуточная -зоной неопределенности. Границамивсех трех зон являются Ч кр1 для р=0,05 и Ч кр2 для р=0,01, как это показанона рисунке.
Взависимости от правила принятия решения(правила вывода), предписанного в данномстатистическом методе возможно дваварианта.
Первыйвариант: альтернативная гипотезапринимается, если Ч эмп ≥Ч кр .

Иливторой вариант: альтернативная гипотезапринимается, если Ч эмп ≤Ч кр .

ПодсчитанноеЧ эмп по какому либостатистическому методу должно обязательнопопасть в одну из трех зон.
Еслиэмпирическое значение попадает в зонунезначимости, то принимается гипотезаН 0об отсутствии различий.
ЕслиЧ эмп попало в зону значимости,принимается альтернативная гипотезаН 1 оналичии различий,а гипотеза Н 0отклоняется.
ЕслиЧ эмп попадает в зонунеопределенности, перед исследователемстоит дилемма. Так, в зависимости отважности решаемой задачи он можетсчитать полученную статистическуюоценку достоверной на уровне 5%, и принять,тем самым гипотезу Н 1 ,отклонив гипотезу Н 0 ,либо — недостовернойна уровне 1%, приняв тем самым, гипотезуН 0 .Подчеркнем, однако, что это именнотот случай, когда психолог может допуститьошибки первого или второго рода. Какуже говорилось выше, в этих обстоятельствахлучше всего увеличить объем выборки.
Подчеркнемтакже, что величина Ч эмп может точно совпастьлибо с Ч кр1 либоЧ кр2 .В первом случае можносчитать, что оценка достоверна точнона уровне в 5% и принять гипотезу Н 1 ,или, напротив, принять гипотезу Н 0 .Во втором случае, как правило,принимается альтернативная гипотезаН 1 о наличии различий,а гипотеза Н 0отклоняется.
Уровень значимости в статистике является важным показателем, отражающим степень уверенности в точности, истинности полученных (прогнозируемых) данных. Понятие широко применяется в различных сферах: от проведения социологических исследований, до статистического тестирования научных гипотез.
Определение
Уровень статистической значимости (или статистически значимый результат) показывает, какова вероятность случайного возникновения исследуемых показателей. Общая статистическая значимость явления выражается коэффициентом р-value (p-уровень). В любом эксперименте или наблюдении существует вероятность, что полученные данные возникли из-за ошибок выборки. Особенно это актуально для социологии.
То есть статистически значимой является величина, чья вероятность случайного возникновения крайне мала либо стремится к крайности. Крайностью в этом контексте считают степень отклонения статистики от нуль-гипотезы (гипотезы, которую проверяют на согласованность с полученными выборочными данными). В научной практике уровень значимости выбирается перед сбором данных и, как правило, его коэффициент составляет 0,05 (5 %). Для систем, где крайне важны точные значения, этот показатель может составлять 0,01 (1 %) и менее.

История вопроса
Понятие уровня значимости было введено британским статистиком и генетиком Рональдом Фишером в 1925 году, когда он разрабатывал методику проверки статистических гипотез. При анализе какого-либо процесса существует определенная вероятность тех либо иных явлений. Трудности возникают при работе с небольшими (либо не очевидными) процентами вероятностей, подпадающими под понятие «погрешность измерений».
При работе со статистическими данными, недостаточно конкретными, чтобы их проверить, ученые сталкивались с проблемой нулевой гипотезы, которая «мешает» оперировать малыми величинами. Фишер предложил для таких систем определить вероятность событий в 5 % (0,05) в качестве удобного выборочного среза, позволяющего отклонить нуль-гипотезу при расчетах.

Введение фиксированного коэффициента
В 1933 году ученые Ежи Нейман и Эгон Пирсон в своих работах рекомендовали заранее (до сбора данных) устанавливать определенный уровень значимости. Примеры использования этих правил хорошо видны во время проведения выборов. Предположим, есть два кандидата, один из которых очень популярен, а второй – малоизвестен. Очевидно, что первый кандидат выборы выиграет, а шансы второго стремятся к нулю. Стремятся – но не равны: всегда есть вероятность форс-мажорных обстоятельств, сенсационной информации, неожиданных решений, которые могут изменить прогнозируемые результаты выборов.
Нейман и Пирсон согласились, что предложенный Фишером уровень значимости 0,05 (обозначаемый символом α) наиболее удобен. Однако сам Фишер в 1956 году выступил против фиксации этого значения. Он считал, что уровень α должен устанавливаться в соответствии с конкретными обстоятельствами. Например, в физике частиц он составляет 0,01.

Значение p-уровня
Термин р-value впервые использован в работах Браунли в 1960 году. P-уровень (p-значение) является показателем, находящимся в обратной зависимости от истинности результатов. Наивысший коэффициент р-value соответствует наименьшему уровню доверия к произведенной выборке зависимости между переменными.
Данное значение отражает вероятность ошибок, связанных с интерпретацией результатов. Предположим, p-уровень = 0,05 (1/20). Он показывает пятипроцентную вероятность того, что найденная в выборке связь между переменными – всего лишь случайная особенность проведенной выборки. То есть, если эта зависимость отсутствует, то при многократных подобных экспериментах в среднем в каждом двадцатом исследовании можно ожидать такую же либо большую зависимость между переменными. Часто p-уровень рассматривается в качестве «допустимой границы» уровня ошибок.
Кстати, р-value может не отражать реальную зависимость между переменными, а лишь показывает некое среднее значение в пределах допущений. В частности, окончательный анализ данных будет также зависеть от выбранных значений данного коэффициента. При p-уровне = 0,05 будут одни результаты, а при коэффициенте, равном 0,01, другие.

Проверка статистических гипотез
Уровень статистической значимости особенно важен при проверке выдвигаемых гипотез. Например, при расчетах двустороннего теста область отторжения разделяют поровну на обоих концах выборочного распределения (относительно нулевой координаты) и высчитывают истинность полученных данных.
Предположим, при мониторинге некоего процесса (явления) выяснилось, что новая статистическая информация свидетельствует о небольших изменениях относительно предыдущих значений. При этом расхождения в результатах малы, не очевидны, но важны для исследования. Перед специалистом встает дилемма: изменения реально происходят или это ошибки выборки (неточность измерений)?
В этом случае применяют либо отвергают нулевую гипотезу (списывают все на погрешность, или признают изменение системы как свершившийся факт). Процесс решения задачи базируется на соотношении общей статистической значимости (р-value) и уровня значимости (α). Если р-уровень
Используемые значения
Уровень значимости зависит от анализируемого материала. На практике используют следующие фиксированные значения:
- α = 0,1 (или 10 %);
- α = 0,05 (или 5 %);
- α = 0,01 (или 1 %);
- α = 0,001 (или 0,1 %).
Чем более точными требуются расчеты, тем меньший коэффициент α используется. Естественно, что статистические прогнозы в физике, химии, фармацевтике, генетике требуют большей точности, чем в политологии, социологии.

Пороги значимости в конкретных областях
В высокоточных областях, таких как физика частиц и производственная деятельность, статистическая значимость часто выражается как соотношение среднеквадратического отклонения (обозначается коэффициентом сигма – σ) относительно нормального распределения вероятностей (распределение Гаусса). σ – это статистический показатель, определяющий рассеивание значений некой величины относительно математических ожиданий. Используется для составления графиков вероятности событий.
В зависимости от области знаний, коэффициент σ сильно разнится. Например, при прогнозировании существования бозона Хиггса параметр σ равен пяти (σ=5), что соответствует значению р-value=1/3,5 млн. При исследованиях геномов уровень значимости может составлять 5×10 -8 , что не являются редкостью для этой области.
Эффективность
Необходимо учитывать, что коэффициенты α и р-value не являются точными характеристиками. Каким бы ни был уровень значимости в статистике исследуемого явления, он не является безусловным основанием для принятия гипотезы. Например, чем меньше значение α, тем больше шанс, что устанавливаемая гипотеза значима. Однако существует риск ошибиться, что уменьшает статистическую мощность (значимость) исследования.
Исследователи, которые зацикливаются исключительно на статистически значимых результатах, могут получить ошибочные выводы. При этом перепроверить их работу затруднительно, так как ими применяются допущения (коими фактически и являются значения α и р-value). Поэтому рекомендуется всегда, наряду с вычислением статистической значимости, определять другой показатель – величину статистического эффекта. Величина эффекта – это количественная мера силы эффекта.
Статистика давно уже стала неотъемлемой частью жизни. С ней люди сталкиваются всюду. На основе статистики делаются выводы о том, где и какие заболевания распространены, что более востребовано в конкретном регионе или среди определенного слоя населения. На основываются даже построения политических программ кандидатов в органы власти. Ими же пользуются и торговые сети при закупке товаров, а производители руководствуются этими данными в своих предложениях.
Статистика играет важную роль в жизни общества и влияет на каждого его отдельного члена даже в мелочах. Например, если по , большинство людей предпочитают темные цвета в одежде в конкретном городе или регионе, то найти яркий желтый плащ с цветочным принтом в местных торговых точках будет крайне затруднительно. Но из каких величин складываются эти данные, оказывающие такое влияние? К примеру, что представляет собой «статистическая значимость»? Что именно понимается под этим определением?
Что это?
Статистика как наука складывается из сочетания разных величин и понятий. Одним из них и является понятие «статистическая значимость». Так называется значение переменных величин, вероятность появления других показателей в которых ничтожно мала.
К примеру, 9 из 10 человек надевают на ноги резиновую обувь во время утренней прогулки за грибами в осенний лес после дождливой ночи. Вероятность того что в какой-то момент 8 из них обуются в парусиновые мокасины — ничтожно мала. Таким образом, в данном конкретном примере число 9 является величиной, которая и называется «статистическая значимость».
Соответственно, если развивать далее приведенный практический пример, обувные магазины закупают к концу летнего сезона резиновые сапожки в большом количестве, чем в другое время года. Так, величина статистического значения оказывает влияние на обычную жизнь.
Разумеется, в сложных подсчетах, допустим, при прогнозе распространения вирусов, учитывается большое число переменных. Но сама суть определения значимого показателя статистических данных — аналогична, вне зависимости от сложности подсчетов и количества непостоянных величин.
Как вычисляют?
Используются при вычислении значения показателя «статистическая значимость» уравнения. То есть можно утверждать, что в этом случае все решает математика. Самым простым вариантом вычисления является цепь математических действий, в которой участвуют следующие параметры:
- два типа результатов, полученных при опросах или изучении объективных данных, к примеру, сумм на которые совершаются покупки, обозначаемые а и b;
- показатель для обеих групп — n;
- значение доли объединенной выборки — p;
- понятие «стандартная ошибка» — SE.
Следующим этапом определяется общий тестовый показатель — t, его значение сравнивается с числом 1,96. 1,96 — это усредненное значение, передающее диапазон в 95 %, согласно функции t-распределения Стьюдента.
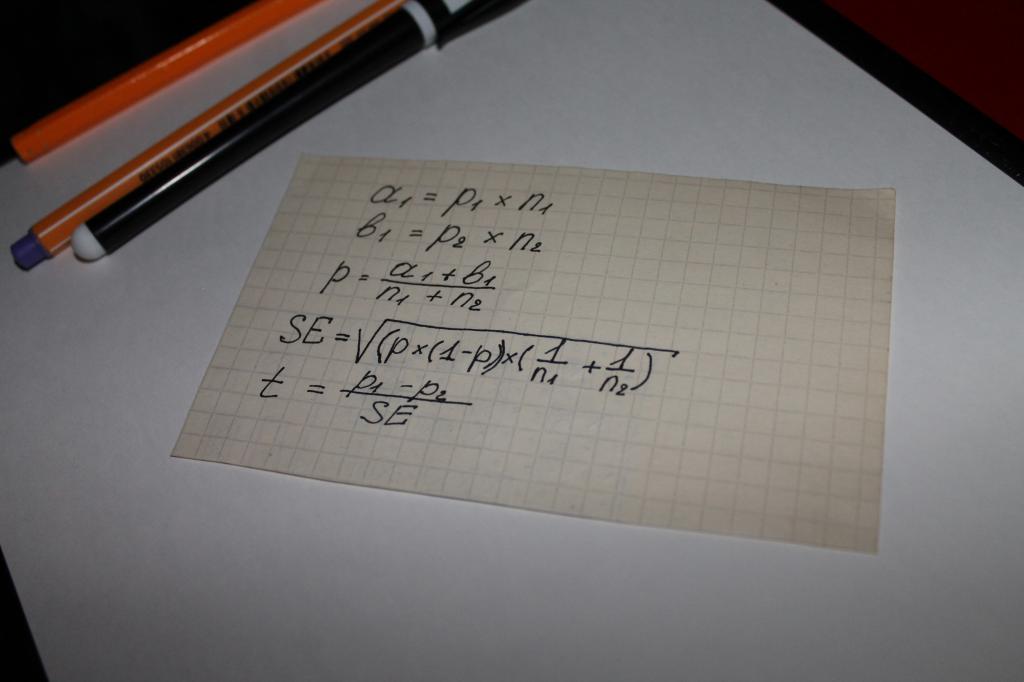
Часто возникает вопрос о том, в чем отличие значений n и p. Этот нюанс просто прояснить при помощи примера. Допустим, вычисляется статистическая значимость лояльности к какому-либо товару или бренду мужчин и женщин.
В этом случае за буквенными обозначениями будет стоять следующее:
- n — число опрошенных;
- p — число довольных продуктом.
Численность опрошенных женщин в этом случае будет обозначено, как n1. Соответственно, мужчин — n2. То же значение будут иметь цифры «1» и «2» у символа p.
Сравнение тестового показателя с усредненными значениями расчетных таблиц Стьюдента и становится тем, что называется «статистическая значимость».
Что понимается под проверкой?
Результаты любого математического вычисления всегда можно проверить, этому учат детей еще в начальных классах. Логично предположить, что раз статистические показатели определяются при помощи цепи вычислений, то и проверяются.
Однако проверка статистической значимости — не только математика. Статистика имеет дело с большим количеством переменных величин и различных вероятностей, далеко не всегда поддающихся расчету. То есть если вернутся к приведенному в начале статьи примеру с резиновой обувью, то логичное построение статистических данных, на которые станут опираться закупщики товаров для магазинов, может быть нарушено сухой и жаркой погодой, которая не типична для осени. В результате этого явления число людей, приобретающих резиновые сапоги, снизится, а торговые точки потерпят убытки. Предусмотреть погодную аномалию математическая формула, разумеется, не в состоянии. Этот момент называется — «ошибка».

Вот как раз вероятность таких ошибок и учитывает проверка уровня вычисленной значимости. В ней учитываются как вычисленные показатели, так и принятые уровни значимости, а также величины, условно называемые гипотезами.
Что такое уровень значимости?
Понятие «уровень» входит в основные критерии статистической значимости. Используется оно в прикладной и практической статистике. Это своего рода величина, учитывающая вероятность возможных отклонений или ошибок.
Уровень основывается на выявлении различий в готовых выборках, позволяет установить их существенность либо же, наоборот, случайность. У этого понятия есть не только цифровые значения, но и их своеобразные расшифровки. Они объясняют то, как нужно понимать значение, а сам уровень определяется сравнением результата с усредненным индексом, это и выявляет степень достоверности различий.

Таким образом, можно представить понятие уровня просто — это показатель допустимой, вероятной погрешности или же ошибки в сделанных из полученных статистических данных выводах.
Какие уровни значимости используются?
Статистическая значимость коэффициентов вероятности допущенной ошибки на практике отталкивается от трех базовых уровней.
Первым уровнем считается порог, при котором значение равно 5 %. То есть вероятность погрешности не превышает уровня значимости в 5 %. Это означает, что уверенность в безупречности и безошибочности выводов, сделанных на основе данных статистических исследований, составляет 95 %.
Вторым уровнем является порог в 1 %. Соответственно, эта цифра означает, что руководствоваться полученными при статистических расчетах данными можно с уверенностью в 99 %.
Третий уровень — 0,1 %. При таком значении вероятность наличия ошибки равна доле процента, то есть погрешности практически исключаются.
Что такое гипотеза в статистике?
Ошибки как понятие разделяются по двум направлениям, касающимся принятия или же отклонения нулевой гипотезы. Гипотеза — это понятие, за которым скрывается, согласно определению, набор иных данных или же утверждений. То есть описание вероятностного распределения чего-либо, относящегося к предмету статистического учета.

Гипотез при простых расчетах бывает две — нулевая и альтернативная. Разница между ними в том, что нулевая гипотеза берет за основу представление об отсутствии принципиальных отличий между участвующими в определении статистической значимости выборками, а альтернативная ей полностью противоположна. То есть альтернативная гипотеза основана на наличии весомой разницы в данных выборок.
Какими бывают ошибки?
Ошибки как понятие в статистике находятся в прямой зависимости от принятия за истинную той или иной гипотезы. Их можно разделить на два направления или же типа:
- первый тип обусловлен принятием нулевой гипотезы, оказавшейся неверной;
- второй — вызван следованием альтернативной.

Первый тип ошибок называется ложноположительным и встречается достаточно часто во всех сферах, где используются статистические данные. Соответственно, ошибка второго типа называется ложноотрицательной.
Для чего нужна регрессия в статистике?
Статистическая значимость регрессии в том, что с ее помощью можно установить, насколько соответствует реальности вычисленная на основе данных модель различных зависимостей; позволяет выявить достаточность или же нехватку факторов для учета и выводов.
Определяется регрессивное значение с помощью сравнения результатов с перечисленными в таблицах Фишера данными. Или же при помощи дисперсионного анализа. Важное значение показатели регрессии имеют при сложных статистических исследованиях и расчетах, в которых участвует большое количество переменных величин, случайных данных и вероятных изменений.
