Контакты
Главная / Люстры

Как правильно записать умножение столбиком с нулями. Как научиться умножать столбиком на однозначные, двузначные, трехзначные числа: правила и алгоритм умножения в столбик. Как объяснить ребенку умножение столбиком? Примеры умножения многозначных чисел в

С лучшей бесплатной игрой учится очень быстро. Проверьте это сами!

Учить таблицу умножения - игра

Попробуйте нашу обучающую электронную игру. Используя её, вы уже завтра сможете решать математические задачи в классе у доски без ответов, не прибегая к табличке, чтобы умножить числа. Стоит только начать играть, и уже минут через 40 будет отличный результат. А для закрепления результата тренируйтесь несколько раз, не забывая о перерывах. В идеале – каждый день (сохраните страницу, чтобы не потерять). Игровая форма тренажера подходит как для мальчиков, так и для девочек.

Результат: 0 очк.

· =

Смотрите ниже шпаргалки в полной форме.


Умножение прямо на сайте (онлайн)

*
Таблица умножения (числа от 1 до 20)
× 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
1 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
2 2 4 6 8 10 12 14 16 18 20 22 24 26 28 30 32 34 36 38 40
3 3 6 9 12 15 18 21 24 27 30 33 36 39 42 45 48 51 54 57 60
4 4 8 12 16 20 24 28 32 36 40 44 48 52 56 60 64 68 72 76 80
5 5 10 15 20 25 30 35 40 45 50 55 60 65 70 75 80 85 90 95 100
6 6 12 18 24 30 36 42 48 54 60 66 72 78 84 90 96 102 108 114 120
7 7 14 21 28 35 42 49 56 63 70 77 84 91 98 105 112 119 126 133 140
8 8 16 24 32 40 48 56 64 72 80 88 96 104 112 120 128 136 144 152 160
9 9 18 27 36 45 54 63 72 81 90 99 108 117 126 135 144 153 162 171 180
10 10 20 30 40 50 60 70 80 90 100 110 120 130 140 150 160 170 180 190 200
11 11 22 33 44 55 66 77 88 99 110 121 132 143 154 165 176 187 198 209 220
12 12 24 36 48 60 72 84 96 108 120 132 144 156 168 180 192 204 216 228 240
13 13 26 39 52 65 78 91 104 117 130 143 156 169 182 195 208 221 234 247 260
14 14 28 42 56 70 84 98 112 126 140 154 168 182 196 210 224 238 252 266 280
15 15 30 45 60 75 90 105 120 135 150 165 180 195 210 225 240 255 270 285 300
16 16 32 48 64 80 96 112 128 144 160 176 192 208 224 240 256 272 288 304 320
17 17 34 51 68 85 102 119 136 153 170 187 204 221 238 255 272 289 306 323 340
18 18 36 54 72 90 108 126 144 162 180 198 216 234 252 270 288 306 324 342 360
19 19 38 57 76 95 114 133 152 171 190 209 228 247 266 285 304 323 342 361 380
20 20 40 60 80 100 120 140 160 180 200 220 240 260 280 300 320 340 360 380 400

Как умножать числа столбиком (видео по математике)

Чтобы потренироваться и быстро выучить, можно также попробовать умножать числа столбиком.

Умножение многозначных или многоразрядных чисел удобно производить письменно в столбик, последовательно умножая каждый разряд. Давайте разберем, как это делать. Начнем с умножения многоразрядного числа на одноразрядное число и постепенно увеличим разрядность второго множителя.

Для того чтобы умножить в столбик два числа, разместите их одно под другим, единицы под единицами, десятки под десятками и так далее. Сравните два множителя и меньший разместите под большим. Затем начинайте умножать каждый разряд второго множителя на все разряды первого множителя.

Умножение многозначного числа на однозначное

Пишем однозначное число под единицами многозначного.

Умножаем 2 последовательно на все разряды первого множителя:

Умножаем на единицы:

8 × 2 = 16

6 пишем под единицами, а 1 десяток запоминаем. Для того, чтобы не забыть пишем 1 над десятками.

Умножаем на десятки:

3 десятка × 2 = 6 десятков + 1 десяток (запоминали) = 7 десятков . Ответ пишем под десятками.

Умножаем на сотни:

4 сотни × 2 = 8 сотен . Ответ пишем под сотнями. В результате получаем:

438 × 2 = 876

Умножение многозначного числа на многозначное

Умножим трехзначное число на двухзначное:

924 × 35

Пишем двухзначное число под трехзначным, единицы под единицами, десятки под десятками.

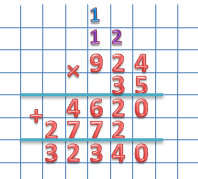1 этап : находим первое неполное произведение , умножив 924 на 5 .

Умножаем 5 последовательно на все разряды первого множителя.

Умножаем на единицы :

4 × 5 = 20 0 пишем под единицами второго множителя, 2 десятка запоминаем.

Умножаем на десятки:

2 десятка × 5 = 10 десятков + 2 десятка (запоминали) = 12 десятков , пишем 2 под десятками второго множителя, 1 запоминаем.

Умножаем на сотни:

9 сотен × 5 = 45 сотен + 1 сотня (запоминали) = 46 сотен , пишем 6 под разрядом сотен, а 4 под разрядом тысяч второго множителя.

924 × 5 = 4620

2 этап : находим второе неполное произведение , умножив 924 на 3 .

Умножаем 3 последовательно на все разряды первого множителя. Ответ пишем под ответом первого этапа, сдвинув его на один разряд влево .

Умножаем на единицы:

4 × 3 = 12 2 пишем под разрядом десятков, 1 запоминаем.

Умножаем на десятки:

2 десятка × 3 = 6 десятков + 1 десяток (запоминали) = 7 десятков , пишем 7 под разрядом сотен.

Умножаем на сотни:

9 сотен × 3 = 27 сотен , 7 пишем в разряд тысяч, а 2 в разряд десятков тысяч.

3 этап : складываем оба неполных произведения.

Складываем поразрядно, учитывая сдвиг.

В результате получаем:

924 × 35 = 32340

Умножим трехзначное число на трехзначное:

Возьмем первый множитель из предыдущего примера, а второй множитель тоже из предыдущего, но больше на 8 сотен:

924 × 835

Итак, два первых этапа такие же, как в предыдущем примере.

3 этап : находим третье неполное произведение , умножив 924 на 8

Умножаем 8 последовательно на все разряды первого множителя. Результат пишем под вторым неполным произведением со сдвигом влево , в разряд сотен.

4 × 8 = 32 , пишем 2 в разряд сотен, 3 запоминаем

2 × 8 = 16 + 3 (запоминали) = 19 , пишем 9 в разряд тысяч, 1 запоминаем

9 × 8 = 72 + 1 (запоминали) = 73 , пишем 73 в разряды сотен и десятков тысяч соответственно.

4 этап : складываем три неполных произведения .

В результате получаем:

924 × 835 = 771540

Итак, сколько разрядов во втором множителе, столько и будет слагаемых в сумме неполных произведений.

Возьмем два множителя с одинаковой разрядностью:

3420 × 2700

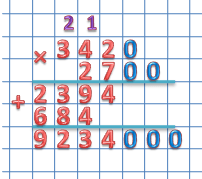При умножении двух чисел оканчивающихся нулями пишем одно число под другим так, чтобы нули обоих множителей остались в стороне.

Теперь умножаем два числа, не обращая внимания на нули:

342 × 27 = 9234

Общее количество нулей приписываем к получившемуся произведению.

В результате получаем:

3420 × 2700 = 9234000

Подведем итог. Для того чтобы письменно в столбик умножить два числа друг на друга, надо :

1. Сравнить два числа и меньшее написать под большим, единицы под единицами, десятки под десятками и так далее. Если числа с нулями, то пишем одно число под другим так, чтобы нули обоих множителей остались в стороне.

2. Умножаем последовательно каждый разряд второго множителя, начиная с единиц, на все разряды первого множителя. На нули внимания не обращаем

3. Неполные произведения пишем друг под другом, сдвигая каждое неполное произведение на один разряд влево. Сколько во втором множителе значащих разрядов (не 0), столько будет неполных произведений.

4 . Складываем все неполные произведения.

5. К полученному результату приписываем нули из обоих множителей.

Вот и все, спасибо, что Вы с нами!

В школе эти действия изучаются от простого к сложному. Поэтому непременно полагается хорошо усвоить алгоритм выполнения названных операций на простых примерах. Чтобы потом не возникло трудностей с делением десятичных дробей в столбик. Ведь это самый сложный вариант подобных заданий.

Этот предмет требует последовательного изучения. Пробелы в знаниях здесь недопустимы. Такой принцип должен усвоить каждый ученик уже в первом классе. Поэтому при пропуске нескольких уроков подряд материал придется освоить самостоятельно. Иначе позже возникнут проблемы не только с математикой, но и другими предметами, связанными с ней.

Второе обязательное условие успешного изучения математики — переходить к примерам на деление в столбик только после того, как освоены сложение, вычитание и умножение.

Ребенку будет трудно делить, если он не выучил таблицу умножения. Кстати, ее лучше учить по таблице Пифагора. Там нет ничего лишнего, да и усваивается умножение в таком случае проще.

Как умножаются в столбик натуральные числа?

Если возникает затруднение в решении примеров в столбик на деление и умножение, то начинать устранять проблему полагается с умножения. Поскольку деление является обратной операцией умножению:

  1. До того как перемножать два числа, на них нужно внимательно посмотреть. Выбрать то, в котором больше разрядов (длиннее), записать его первым. Под ним разместить второе. Причем цифры соответствующего разряда должны оказаться под тем же разрядом. То есть самая правая цифра первого числа должна быть над самой правой второго.
  2. Умножьте крайнюю правую цифру нижнего числа на каждую цифру верхнего, начиная справа. Запишите ответ под чертой так, чтобы его последняя цифра была под той на которую умножали.
  3. То же повторите с другой цифой нижнего числа. Но результат от умножения при этом нужно сместить на одну цифру влево. При этом его последняя цифра окажется под той, на которую умножали.

Продолжать такое умножение в столбик до тех пор, пока не закончатся цифры во втором множителе. Теперь их нужно сложить. Это и будет искомый ответ.

Алгоритм умножения в столбик десятичных дробей

Сначала полагается представить, что даны не десятичные дроби, а натуральные. То есть убрать из них запятые и далее действовать так, как описано в предыдущем случае.

Отличие начинается, когда записывается ответ. В этот момент необходимо сосчитать все цифры, которые стоят после запятых в обеих дробях. Именно столько их нужно отсчитать от конца ответа и там поставить запятую.

Удобно проиллюстрировать этот алгоритм на примере: 0,25 х 0,33:

С чего начать обучение делению?

До того как решать примеры на деление в столбик, полагается запомнить названия чисел, которые стоят в примере на деление. Первое из них (то, которое делится) — делимое. Второе (на него делят) — делитель. Ответ — частное.

После этого на простом бытовом примере объясним суть этой математической операции. Например, если взять 10 конфет, то поделить их поровну между мамой и папой легко. А как быть, если нужно раздать их родителям и брату?

После этого можно знакомиться с правилами деления и осваивать их на конкретных примерах. Сначала простых, а потом переходить ко все более сложным.

Алгоритм деления чисел в столбик

Вначале представим порядок действий для натуральных чисел, делящихся на однозначное число. Они будут основой и для многозначных делителей или десятичных дробей. Только тогда полагается внести небольшие изменения, но об этом позже:

  • До того как делать деление в столбик, нужно выяснить, где делимое и делитель.
  • Записать делимое. Справа от него - делитель.
  • Прочертить слева и снизу около последнего уголок.
  • Определить неполное делимое, то есть число, которое будет минимальным для деления. Обычно оно состоит из одной цифры, максимум из двух.
  • Подобрать число, которое будет первым записано в ответ. Оно должно быть таким, сколько раз делитель помещается в делимом.
  • Записать результат от умножения этого числа на делитель.
  • Написать его под неполным делимом. Выполнить вычитание.
  • Снести к остатку первую цифру после той части, которая уже разделена.
  • Снова подобрать число для ответа.
  • Повторить умножение и вычитание. Если остаток равен нулю и делимое закончилось, то пример сделан. В противном случае повторить действия: снести цифру, подобрать число, умножить, вычесть.

Как решать деление в столбик, если в делителе больше одной цифры?

Сам алгоритм полностью совпадает с тем, что был описан выше. Отличием будет количество цифр в неполном делимом. Их теперь минимум должно быть две, но если они оказываются меньше делителя, то работать полагается с первыми тремя цифрами.

Существует еще один нюанс в таком делении. Дело в том, что остаток и снесенная к нему цифра иногда не делятся на делитель. Тогда полагается приписать еще одну цифру по порядку. Но при этом в ответ необходимо поставить ноль. Если осуществляется деление трехзначных чисел в столбик, то может потребоваться снести больше двух цифр. Тогда вводится правило: нолей в ответе должно быть на один меньше, чем количество снесенных цифр.

Рассмотреть такое деление можно на примере - 12082: 863.

  • Неполным делимым в нем оказывается число 1208. В него число 863 помещается только один раз. Поэтому в ответ полагается поставить 1, а под 1208 записать 863.
  • После вычитания получается остаток 345.
  • К нему нужно снести цифру 2.
  • В числе 3452 четыре раза умещается 863.
  • Четверку необходимо записать в ответ. Причем при умножении на 4 получается именно это число.
  • Остаток после вычитания равен нулю. То есть деление закончено.

Ответом в примере будет число 14.

Как быть, если делимое заканчивается на ноль?

Или несколько нолей? В этом случае нулевой остаток получается, а в делимом еще стоят нули. Отчаиваться не стоит, все проще, чем может показаться. Достаточно просто приписать к ответу все нули, которые остались не разделенными.

Например, нужно поделить 400 на 5. Неполное делимое 40. В него 8 раз помещается пятерка. Значит, в ответ полагается записать 8. При вычитании остатка не остается. То есть деление закончено, но в делимом остался ноль. Его придется приписать к ответу. Таким образом, при делении 400 на 5 получается 80.

Что делать, если разделить нужно десятичную дробь?

Опять же, это число похоже на натуральное, если бы не запятая, отделяющая целую часть от дробной. Это наводит на мысль о том, что деление десятичных дробей в столбик подобно тому, которое было описано выше.

Единственным отличием будет пункт с запятой. Ее полагается поставить в ответ сразу, как только снесена первая цифра из дробной части. По-другому это можно сказать так: закончилось деление целой части — поставь запятую и продолжай решение дальше.

Во время решения примеров на деление в столбик с десятичными дробями нужно помнить, что в части после запятой можно приписать любое количество нолей. Иногда это нужно для того, чтобы доделить числа до конца.

Деление двух десятичных дробей

Оно может показаться сложным. Но только вначале. Ведь то, как выполнить деление в столбик дробей на натуральное число, уже понятно. Значит, нужно свести этот пример к уже привычному виду.

Сделать это легко. Нужно умножить обе дроби на 10, 100, 1 000 или 10 000, а может быть, на миллион, если этого требует задача. Множитель полагается выбирать исходя из того, сколько нолей стоит в десятичной части делителя. То есть в результате получится, что делить придется дробь на натуральное число.

Причем это будет в худшем случае. Ведь может получиться так, что делимое от этой операции станет целым числом. Тогда решение примера с делением в столбик дробей сведется к самому простому варианту: операции с натуральными числами.

В качестве примера: 28,4 делим на 3,2:

  • Сначала их необходимо умножить на 10, поскольку во втором числе после запятой стоит только одна цифра. Умножение даст 284 и 32.
  • Их полагается разделить. Причем сразу все число 284 на 32.
  • Первым подобранным числом для ответа является 8. От его умножения получается 256. Остатком будет 28.
  • Деление целой части закончилось, и в ответ полагается поставить запятую.
  • Снести к остатку 0.
  • Снова взять по 8.
  • Остаток: 24. К нему приписать еще один 0.
  • Теперь брать нужно 7.
  • Результат умножения - 224, остаток - 16.
  • Снести еще один 0. Взять по 5 и получится как раз 160. Остаток — 0.

Деление закончено. Результат примера 28,4:3,2 равен 8,875.

Что делать, если делитель равен 10, 100, 0,1, или 0,01?

Так же как и с умножением, деление в столбик здесь не понадобится. Достаточно просто переносить запятую в нужную сторону на определенное количество цифр. Причем по этому принципу можно решать примеры как с целыми числами, так и с десятичными дробями.

Итак, если нужно делить на 10, 100 или 1 000, то запятая переносится влево на такое количество цифр, сколько нулей в делителе. То есть, когда число делится на 100, запятая должна сместиться влево на две цифры. Если делимое — натуральное число, то подразумевается, что запятая стоит в его конце.

Это действие дает такой же результат, как если бы число было необходимо умножить на 0,1, 0,01 или 0,001. В этих примерах запятая тоже переносится влево на количество цифр, равное длине дробной части.

При делении на 0,1 (и т. д.) или умножении на 10 (и т. д.) запятая должна переместиться вправо на одну цифру (или две, три, в зависимости от количества нулей или длины дробной части).

Стоит отметить, что количества цифр, данных в делимом, может быть недостаточным. Тогда слева (в целой части) или справа (после запятой) можно приписать недостающие нули.

Деление периодических дробей

В этом случае не удастся получить точный ответ при делении в столбик. Как решать пример, если встретилась дробь с периодом? Здесь полагается переходить к обыкновенным дробям. А потом выполнять их деление по изученным ранее правилам.

Например разделить нужно 0,(3) на 0,6. Первая дробь — периодическая. Она преобразуется в дробь 3/9, которая после сокращения даст 1/3. Вторая дробь — конечная десятичная. Ее записать обыкновенной еще проще: 6/10, что равно 3/5. Правило деления обыкновенных дробей предписывает заменять деление умножением и делитель — обратным числом. То есть пример сводится к умножению 1/3 на 5/3. Ответом будет 5/9.

Если в примере разные дроби...

Тогда возможны несколько вариантов решения. Во-первых, обыкновенную дробь можно попытаться перевести в десятичную. Потом делить уже две десятичные по указанному выше алгоритму.

Во-вторых, каждая конечная десятичная дробь может быть записана в виде обыкновенной. Только это не всегда удобно. Чаще всего такие дроби оказываются огромными. Да и ответы получаются громоздкими. Поэтому первый подход считается более предпочтительным.

И умножение. Как раз об операции умножения и пойдет речь в этой статье.

Умножение чисел

Умножение чисел осваивается детьми во втором классе, и ничего в этом сложного нет. Сейчас мы рассмотрим умножение на примерах.

Пример 2*5 . Это значит либо 2+2+2+2+2, либо 5+5. Берем 5 два раза или 2 пять раз. Ответ, соответственно, 10.

Пример 4*3 . Аналогично, 4+4+4 или 3+3+3+3. Три раза по 4 или четыре раза по 3. Ответ 12.

Пример 5*3 . Делаем так же как и предыдущие примеры. 5+5+5 или 3+3+3+3+3. Ответ 15.

Формулы умножения

Умножение – это сумма одинаковых чисел, например, 2 * 5 = 2 + 2 + 2 + 2 + 2 или 2 * 5 = 5 + 5. Формула умножения:

Где, а – любое число, n – число слагаемых а. Допустим, а=2, тогда 2+2+2=6, тогда n=3 умножая 3 на 2, получаем 6.Рассмотрим в обратном порядке. Например, дано: 3 * 3, то есть. 3 умножить на 3 – это значит, что тройку надо взять 3 раза: 3 + 3 + 3 = 9. 3 * 3=9.

Сокращенное умножение

Сокращенное умножение – сокращение операции умножения в определенных случаях, и специально для этого выведены формулы сокращенного умножения. Которые помогут сделать вычисления наиболее рациональными и быстрыми:

Формулы сокращенного умножения

Пусть a, b принадлежат R, тогда:

    Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого выражения на второе плюс квадрат второго выражения. Формула: (a+b)^2 = a^2 + 2ab + b^2

    Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого выражения на второе плюс квадрат второго выражения. Формула: (a-b)^2 = a^2 - 2ab + b^2

    Разность квадратов двух выражений равна произведению разности этих выражений и их суммы. Формула: a^2 - b^2 = (a - b)(a + b)

    Куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго плюс куб второго выражения. Формула: (a + b)^3 = a^3 + 3a(^2)b + 3ab^2 + b^3

    Куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго минус куб второго выражения. Формула: (a-b)^3 = a^3 - 3a(^2)b + 3ab^2 - b^3

    Сумма кубов a^3 + b^3 = (a + b)(a^2 - ab + b^2)

    Разность кубов двух выражений равна произведению суммы первого и второго выражения на неполный квадрат разности этих выражений. Формула: a^3 - b^3 = (a - b)(a^2 + ab + b^2)

Запишитесь на курс "Ускоряем устный счет, НЕ ментальная арифметика", чтобы научиться быстро и правильно складывать, вычитать, умножать, делить, возводить числа в квадрат и даже извлекать корни. За 30 дней вы научитесь использовать легкие приемы для упрощения арифметических операций. В каждом уроке новые приемы, понятные примеры и полезные задания.

Умножение дробей

Рассматривая сложение и вычитание дробей, прозвучало правило, приведения дробей к общему знаменателю, чтобы выполнить расчет. При умножении этого делать не надо ! При умножении двух дробей, умножается знаменатель на знаменатель, а числитель на числитель.

Например, (2/5) * (3 * 4). Умножим две трети на одну четверть. Умножаем знаменатель на знаменатель, а числитель на числитель: (2 * 3)/(5 * 4), тогда 6/20, совершаем сокращение, получаем 3/10.

Умножение 2 класс

Второй класс – это только начала изучения умножения, поэтому второклассники решают простейшие задачки на замену сложения умножением, умножают числа, учат таблицу умножения.Давайте рассмотрим задачи на умножение уровня второго класса:

    Олег живет в пяти этажном доме, на самом верхнем этаже. Высота одного этажа равняется 2 метрам. Какова высота дома?

    В коробке находятся 10 упаковок с печеньем. В каждой упаковке их 7 штук. Сколько печенья в коробке?

    Миша расставил свои игрушечные машинки в ряд. В каждом ряду их 7, а рядов всего 8. Сколько у Миши машинок?

    В столовой стоят 6 столов, а за каждым столом задвинуты 5 стульев. Сколько стульев в столовой?

    Мама с магазина принесла 3 пакета с апельсинами. В пакетах находятся по 22 апельсина. Сколько апельсиновпринесла мама?

    В саду растет 9 кустов клубники, а на каждом кустике растет 11 ягод. Сколько ягод растет на всех кустиках?

    Рома положил друг за другом 8 деталей трубы, одинакового размера по 2 метра. Какова длина полной трубы?

    В школу родители на первое сентября привезли детей. Приехало 12 машин, в каждой было по 2 ребенка. Сколькодетей привезли родители на этих машинах?

Умножение 3 класс

В третьем классе даются уже более серьезные задания. Помимо умножения будет так же проходиться Деление .

Среди заданий на умножение будет: умножение двузначных чисел, умножение столбиком, замена сложения умножением и наоборот.

Умножение столбиком:

Умножение столбиком – самый простой способ перемножить большие числа. Рассмотрим данный метод на примередвух чисел 427 * 36.

1 шаг . Запишем числа друг под другом, так чтобы 427 было на верху, а 36 внизу, то есть 6 под 7, 3 под 2.

2 шаг . Умножение начинаем с крайней правой цифры нижнего числа. То есть порядок умножения таков: 6 * 7, 6 * 2, 6 * 4, затем так же с тройкой: 3 * 7, 3 * 2, 3 * 4.

Итак, умножаем сначала 6 на 7, ответ:42. Записываем так: так как получилось 42, то 4 – десятки, а 2 – единицы, запись происходит аналогично сложению, а значит 2 записываем под шестеркой, а 4 прибавляем к двойке числа 427.

3 шаг . Затем аналогично делаем с 6 * 2. Ответ: 12. Первый десяток, который прибавляется к четверке числа 427, а второй – единицы. Складываем полученную двойку с четверкой от предыдущего умножения.

4 шаг . Умножаем 6 на 4. Ответа 24 и прибавляем 1 от предыдущего умножения. Получаем 25.

Итак, умножив 427 на 6, получился ответ 2562

ЗАПОМНИТЕ! Результат второго умножения нужно начать записывать под ВТОРОЙ цифрой первого результата!

5 шаг . Совершаем аналогичные действия с цифрой 3. Получаем ответ умножения 427 * 3=1281

6 шаг . Затем полученные ответы при умножении складываем и получаем итоговый ответ умножения 427 * 36. Ответ: 15372.

Умножение 4 класс

Четвертый класс – это уже умножение только больших чисел. Вычисление выполняются методом умножения в столбик. Метод описан выше доступным языком.

Например, найти произведение следующих пар чисел:

  1. 988 * 98 =
  2. 99 * 114 =
  3. 17 * 174 =
  4. 164 * 19 =

Презентация на умножение

Скачайте презентацию на умножение с простейшими заданиями для второклассников. Презентация поможет детям лучше ориентироваться в этой операции, потому что она составлена красочно и в игровом стиле – в лучшем варианте для обучения ребенка!

Таблица умножения

Таблица умножения учится каждым школьником во втором классе. Ее обязан знать каждый!

Запишитесь на курс "Ускоряем устный счет, НЕ ментальная арифметика", чтобы научиться быстро и правильно складывать, вычитать, умножать, делить, возводить числа в квадрат и даже извлекать корни. За 30 дней вы научитесь использовать легкие приемы для упрощения арифметических операций. В каждом уроке новые приемы, понятные примеры и полезные задания.

Примеры на умножение

Умножение на однозначное

  1. 9 * 5 =
  2. 9 * 8 =
  3. 8 * 4 =
  4. 3 * 9 =
  5. 7 * 4 =
  6. 9 * 5 =
  7. 8 * 8 =
  8. 6 * 9 =
  9. 6 * 7 =
  10. 9 * 2 =
  11. 8 * 5 =
  12. 3 * 6 =

Умножение на двузначное

  1. 4 * 16 =
  2. 11 * 6 =
  3. 24 * 3 =
  4. 9 * 19 =
  5. 16 * 8 =
  6. 27 * 5 =
  7. 4 * 31 =
  8. 17 * 5 =
  9. 28 * 2 =
  10. 12 * 9 =

Умножение двузначное на двузначное

  1. 24 * 16 =
  2. 14 * 17 =
  3. 19 * 31 =
  4. 18 * 18 =
  5. 10 * 15 =
  6. 15 * 40 =
  7. 31 * 27 =
  8. 23 * 25 =
  9. 17 * 13 =

Умножение трехзначных чисел

  1. 630 * 50 =
  2. 123 * 8 =
  3. 201 * 18 =
  4. 282 * 72 =
  5. 96 * 660 =
  6. 910 * 7 =
  7. 428 * 37 =
  8. 920 * 14 =

Игры на развитие устного счета

Специальные развивающие игры разработанные при участии российских ученых из Сколково помогут улучшить навыки устного счета в интересной игровой форме.

Игра "Быстрый счет"

Игра «быстрый счет» поможет вам усовершенствовать свое мышление . Суть игры в том, что на представленной вам картинке, потребуется выбрать ответ «да» или «нет» на вопрос «есть ли 5 одинаковых фруктов?». Идите за своей целью, а поможет вам в этом данная игра.

Игра "Математические матрицы"

«Математические матрицы» великолепное упражнение для мозга детей , которое поможет вам развить его мыслительную работу, устный счет, быстрый поиск нужных компонентов, внимательность. Суть игры заключается в том, что игроку предстоит из предложенных 16 чисел найти такую пару, которая в сумме даст данное число, например на картинке ниже данное число «29», а искомая пара «5» и «24».

Игра "Числовой охват"

Игра «числовой охват» нагрузит вашу память во время занятий с данным упражнением.

Суть игры – запомнить цифру, на запоминание которой отводится около трех секунд. Затем нужно ее воспроизвести. По мере прохождения этапов игры, количество цифр растет, начинаете с двух и далее.

Игра "Угадай операцию"

Игра «Угадай операцию» развивает мышление и память. Главная суть игры надо выбрать математический знак, чтобы равенство было верным. На экране даны примеры, посмотрите внимательно и поставьте нужный знак «+» или «-», так чтобы равенство было верным. Знак «+» и «-» расположены внизу на картинке, выберите нужный знак и нажмите на нужную кнопку. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Игра "Упрощение"

Игра «Упрощение» развивает мышление и память. Главная суть игры надо быстро выполнить математическую операцию. На экране нарисован ученик у доски, и дано математическое действие, ученику надо посчитать этот пример и написать ответ. Внизу даны три ответа, посчитайте и нажмите нужное вам число с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Игра "Быстрое сложение"

Игра «Быстрое сложение» развивает мышление и память. Главная суть игры выбирать цифры, сумма которых равна заданной цифре. В этой игре дана матрица от одного до шестнадцати. Над матрицей написано заданное число, надо выбрать цифры в матрице так, чтобы сумма этих цифр была равна заданной цифре. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Игра "Визуальная геометрия"

Игра «Визуальная геометрия» развивает мышление и память. Главная суть игры быстро считать количество закрашенных объектов и выбрать его из списка ответов. В этой игре на экране на несколько секунд показываются синие квадратики, их надо быстро посчитать, потом они закрываются. Снизу под таблицей написаны четыре числа, надо выбрать одно правильное число и нажать на него с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Игра "Математические сравнения"

Игра «Математические сравнения» развивает мышление и память. Главная суть игры сравнить числа и математические операции. В этой игре надо сравнить два числа. На верху, написан вопрос, прочитайте его и ответьте правильно на поставленный вопрос. Ответить можно при помощи кнопок расположенных внизу. Там нарисованы три кнопки «левое», «равно» и «правое». Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Развитие феноменального устного счета

Мы рассмотрели лишь верхушку айсберга, чтобы понять математику лучше - записывайтесь на наш курс: Ускоряем устный счет.

Из курса вы не просто узнаете десятки приемов для упрощенного и быстрого умножения, сложения, умножения, деления, высчитывания процентов, но и отработаете их в специальных заданиях и развивающих играх! Устный счет тоже требует много внимания и концентрации, которые активно тренируются при решении интересных задач.

Скорочтение за 30 дней

Увеличьте скорость чтения в 2-3 раза за 30 дней. Со 150-200 до 300-600 слов в минуту или с 400 до 800-1200 слов в минуту. В курсе используются традиционные упражнения для развития скорочтения, техники ускоряющие работу мозга, методика прогрессивного увеличения скорости чтения, разбирается психология скорочтения и вопросы участников курса. Подходит детям и взрослым, читающим до 5000 слов в минуту.

Развитие памяти и внимания у ребенка 5-10 лет

В курс входит 30 уроков с полезными советами и упражнениями для развития детей. В каждом уроке полезный совет, несколько интересных упражнений, задание к уроку и дополнительный бонус в конце: развивающая мини-игра от нашего партнера. Длительность курса: 30 дней. Курс полезно проходить не только детям, но и их родителям.

Супер-память за 30 дней

Запоминайте нужную информацию быстро и надолго. Задумываетесь, как открывать дверь или помыть голову? Уверен, что нет, ведь это часть нашей жизни. Легкие и простые упражнения для тренировки памяти можно сделать частью жизни и выполнять понемногу среди дня. Если съесть суточную норму еды за раз, а можно есть порциями в течение дня.

Секреты фитнеса мозга, тренируем память, внимание, мышление, счет

Мозгу, как и телу нужен фитнес. Физические упражнения укрепляют тело, умственные развивают мозг. 30 дней полезных упражнений и развивающих игр на развитие памяти, концентрации внимания, сообразительности и скорочтения укрепят мозг, превратив его в крепкий орешек.

Деньги и мышление миллионера

Почему бывают проблемы с деньгами? В этом курсе мы подробно ответим на этот вопрос, заглянем вглубь проблемы, рассмотрим наши взаимоотношения с деньгами с психологической, экономической и эмоциональных точек зрения. Из курса Вы узнаете, что нужно делать, чтобы решить все свои финансовые проблемы, начать накапливать деньги и в дальнейшем инвестировать их.

Знание психологии денег и способов работы с ними делает человека миллионером. 80% людей при увеличении доходов берут больше кредитов, становясь еще беднее. С другой стороны миллионеры, которые всего добились сами, снова заработают миллионы через 3-5 лет, если начнут с нуля. Этот курс учит грамотному распределению доходов и уменьшению расходов, мотивирует учиться и добиваться целей, учит вкладывать деньги и распознавать лохотрон.

Ребята, давайте повторим, что такое однозначное, двузначное и трехзначное число.

Однозначное число - это число, для записи которого нужен один знак.
Например: 1, 3, 5, 4, ...
Наверное, вы уже догадались, что однозначным числом являются цифры, когда они записаны, как число. Они состоят из единиц.

Двузначное число - это число, для записи которого, нужно два знака. Например, все числа от 10 до 99 являются двузначными числами. Они состоят из десятков и единиц.

Когда дети начинают разбивать номера?

Разделение проводится в ключевой стадии 1, чтобы дети знали, что двузначное число состоит из десятков и единиц. Идея состоит в том, что ребенок соединяет стрелки вместе, чтобы цифры соответствовали. Это два часто используемых метода для добавления больших чисел.

Учитель может начать обучать детей добавлять двузначные и трехзначные числа в году 3 путем разбиения на разделы. Причиной этого является то, что он помогает детям мысленно добавлять кратные десять и кратные 100. Дети в 3-м году должны добавить также научиться добавлять трехзначные числа с помощью, поэтому ваш ребенок, вероятно, столкнется с обоими из этих методов.

Трехзначное число - это число, для записи которых, нужны три знака. Вы уже догадались, что все числа от 100 до 999 являются трехзначными. Они содержат единицы, десятки и сотни.
Ребята, ответьте на вопрос: сколько существует трехзначных чисел?

Давайте на примере разберём, как нужно выполнить операцию умножения многозначного числа на однозначное число .

Прежде всего запомните правило умножение на ноль и единицу.
Это правило гласит:
Число * 0 = 0
Число * 1 = Число

Разделение в умножении

Детям 3-го года также необходимо умножить двузначные числа на одноразрядное число. Их обычно обучают этому разбиению, например. Как только учителя очень уверены, что ребенок знает, как умножить кратные десять и сто, они часто позволят ребенку перейти на более быстрый метод столбцов.

В 6-й год дети должны начать вычислять. Чтобы это стало проще, учитель может показать им, как разделять десятичные числа. Это читается так, как четыре раза шесть равно двадцать четыре или просто четыре раза шесть - двадцать четыре. Знание умножения очень важно. Итак, если вы слабы в умножении, вы должны попытаться достичь уровня владения следующим «таблицей времени».

Примеры.
5 * 0 = 0;
18 * 0 = 0;
4506 * 0 = 0
1 * 34 = 34;
2384 * 1 = 2384;
1 * 47586 = 47586

Для умножения многозначных чисел часто применяют метод умножения столбиком, который мы будем применять в наших примерах.

Умножим многозначное число на число, отличное от 0 или 1.
Рассмотрим примеры.
Возьмем числа 348 и 4. Для нашего удобства запишем их в столбик. Начнем умножение с крайнего правого столбца и перемножим числа 4 и 8. Получим число 32. Число 2 записываем строго под числами 8 и 4. А число 30 переводим в соседний разряд (разряд десяток). При переносе числа в более старший разряд, например, из единиц в десятки, это число теряет 0. Теперь умножаем 4 и 4 и получим 16. Прибавим 3 от предыдущего умножения. В итоге, у нас получим 19. Число 9 пишем под числом 4 (левее цифры 2), а 1 переводим в соседний разряд (разряд сотен). Затем перемножаем числа 3 и 4 и к результату приплюсуем 1 от предыдущего действия. В итоге, получаем 13. Записываем его полностью, т.к. это наше последнее действие. В итоге, мы получаем произведение чисел 348 на 4, которое равно 1392.

Умножение больших чисел

Ваша уверенность и умение учиться математике будет во многом зависеть от ваших знаний о размножении. Итак, вы должны стремиться справиться с вышеуказанным «таблицей времени».

  • Продукт является результатом умножения двух чисел.
  • Чтобы вычислить 8 Ч 9, напомним «таблицу восьми раз».
Чтобы умножить большое число на другое число, мы можем использовать короткое умножение или длительное умножение.

Чтобы умножить большое число на одноразрядное число, введите цифры по вертикали, а большее число будет умножено на меньшее число. Чтобы вычислить 89 Ч 7, установите его вертикально с меньшим числом, помещенным под большим числом, как показано ниже. Теперь, вычислите 7 Ч 8 и добавьте 6, чтобы получить Это написано, как показано ниже.

Примеры умножения многозначного числа на двузначное число

В этом примере рассмотрим умножение трехзначного числа на двузначное. Возьмем числа 925 и 38.
Весь процесс умножение делится на несколько частей.
Первая часть - умножение числа 925 на число 8. Для удобства запишем их в столбик.
Как обычно, при умножении в столбик мы начнем свои действия с крайнего правого столбца. Там записаны числа 5 и 8, перемножив, которые получим число 40. Записываем число 0 под числамии 5 и 8. Не забываем 40 перенести в следующий разряд (разряд десяток). Теперь перемножаем числа 2 и 8. Получаем 16. Не забываем прибавить число 4, которое осталось после выполнения предыдущего действия (при перемножении 8 и 5). Получим число 20. Число 0 записываем под числом 3 рядом с предыдущим числом 0, а 20 переносим в следующий разряд (разряд сотен). И последнее действие первой части - это перемножение чисел 9 и 8. Произведение этих чисел равно 72. Добавим к произведению число 2 и получим число 74. Запишем его полностью.
Вторая часть - умножение числа 925 на число 3. Не будем рассматривать эту часть так же подробно, как и предыдущую, а просто запишем результат произведения этих чисел. При записи произведения чисел второй части нужно помнить, что запись надо начинать не с крайнего правого столбца, а со смещением на единицу. В нашем примере первое число надо записать строго под числами 2, 3,0. Смотрите рисунок.
Третья часть - получение суммы чисел. Это заключительный этап, на котором нам нужно получить сумму от первого произведения - 7400 и от второго произведения - 2775. Суммируем, соблюдая правила, которые используются при сложении в столбик. На последнем рисунке представлен результат умножения двузначного числа 38 на трехзначное число 925.

Самое главное правило, с которого мы начинаем изучать умножение в столбик:

Мы часто излагаем решение следующим образом. Умножение 38 на 60 быстрее, чем умножение на 60 на 38, поскольку 60 содержит нуль. Умножение на 385 на 500 быстрее, чем умножение на 500 на 385, поскольку 500 содержит два нуля. Чтобы умножить два больших числа , напишите числа по вертикали, а большее число будет умножено на меньшее число, которое называется множителем. Мы используем таблицу раз, чтобы найти произведение большего числа с каждой цифрой в множителе, добавляя результаты. Например, если умножающая цифра находится в столбце сотен, добавьте два нуля для столбца десятков и столбца единиц.

  • Итак, разместите 3 в столбце единиц и несите 6.
  • Затем вычислите 7 Ч 8 и добавьте 6, чтобы получить 62.
  • В столбце единиц помещается нуль.
  • Затем мы вычисляем 6 Ч 38, как показано выше.
  • В столбце единиц помещается нуль, а также столбец десятков.
  • Затем мы вычисляем 5 Ч 385, как показано выше.
  • Не забывайте добавлять нуль для каждого значения места после умножающей цифры.
  • Чтобы умножить 269 на 78, место 78 ниже.
  • Затем вычислим 8 Ч 269 и 70 Ч 269, как показано выше.
Это известно как Коммутативный закон для умножения.

Умножение в столбик на двузначное число

Пример: 46 умножить на 73

Под числом 46 записываем число 73 по правилу:

Единицы записываем под единицами, а десятки под десятками

1 Умножать начинаем с единиц.

3 умножим на 6. Получится 18.

  • 18 единиц – это 1 десяток и 8 единиц.
  • 8 единиц пишем под единицами, а 1 десяток запоминаем и прибавим к десяткам.

Теперь 3 умножим на 4 десятка. Получится 12.

Ярлык №1: Квадратирование номеров в 50-х годах

Любой может хорошо разбираться в математике с ярлыками Майка Бистера. Теперь, если число с шага 2 меньше 10, вы должны поставить перед ним ноль.

Ярлык 2: Умножение двух чисел в 90-х годах вместе

Когда вы умножаете два числа в 90-х вместе, в круглых скобках рядом с каждым номером указывается, как далеко это число находится далеко от.

Умножим трехзначное число на двухзначное

Это один из моих любимых трюков, потому что он прост и поражает любого, кто его видит. Попросите кого-нибудь выбрать два числа ниже 10 и написать один поверх другого. Попросите человека добавить их и поставить ответ прямо под двумя номерами. Попросите человека продолжить добавление нижних двух чисел в столбец и продолжайте суммирование итоговой суммы до тех пор, пока у вас не будет всего десять чисел. Затем добавьте ему весь столбец. Пример: кто-то выбирает числа 4 и 7 и записывает 4 сверху. Следующее число в серии будет потому, что 4 7 = Затем, добавив нижние два числа в столбец, следующее число будет 18, потому что 7 11 = Он должен продолжать делать это, пока у него не будет всего десять чисел, а затем он добавит всю колонку.

12 десятков, да ещё 1, всего 13 десятков.

Сотен в этом примере нет, поэтому сразу на месте сотен пишем 1.

138 - это первое неполное произведение.

2 Умножаем десятки.

7 десятков умножить на 6 единиц получится 42 десятка.

  • 42 десятка это 4 сотни и 2 десятка.
  • 2 десятка пишем под десятками. 4 запомним и прибавим к сотням.

7 десятков умножить на 4 десятка получится 28 сотен. 28 сотен, да ещё 4 получится 32 сотни.

Столбец может выглядеть примерно так. Вы быстро взглянете на цифры и скажете ему, что все десять цифр добавляют. Все, что вам нужно сделать, это посмотреть на 76 и добавить десятки цифра к нему, 76 7 = Затем наложите на одну цифру 76 на конец. Если человек выбрал два больших числа, таких как 8 и 9, седьмое число может быть трехзначным числом. Столбец будет выглядеть так.

Какие ошибки при умножении можно сделать и как их избежать

Седьмой номер в этом случае. Здесь мы рассмотрим, как умножать двузначные числа. Сначала использовал метод, названный Прямым методом Яковом Трахтенбергом, а второй - методом «двух пальцев». Оба эти метода будут работать для любых комбинаций двухзначных чисел.

  • 32 сотни – это 3 тысячи и 2 сотни.
  • 2 сотни пишем под сотнями, а 3 тысячи запомним и прибавим к тысячам.

Тысяч в этом примере нет, поэтому сразу на месте тысяч пишу 3.

3220 – это второе неполное произведение.

3 Складываем первое и второе неполные произведения по правилу сложения в столбик.

138 плюс 3220 получится 3358.

Если вы заинтересованы в том, чтобы умножить цифры до двенадцати, взгляните на них. Прямой метод редко преподается в школах, но известен на протяжении веков. В школе вас обычно учат записывать результат умножения каждой цифры множителя на отдельную строку , а затем суммирование общей суммы.

Умножение многозначного числа на многозначное

Вместо этого вы пишете только ответ. Для этого вы делаете пару вычислений на каждом шаге. Пары, которые приравниваются ни к чему, игнорируются. Эти пары называются внешними и внутренними парами. Внешняя пара всегда соединяет единичную цифру множителя с цифрой, в которой мы сейчас смотрим. Внутренняя пара всегда соединяет десятки цифр с цифрой справа от цифры, над которой мы работаем в мультипликаторе.

Читаем ответ: 46 умножить на 73 получится 3358

(Кликните по картинке)

Компоненты действия умножения

(Кликните по картинке)

Образец рассуждения
во время записи
умножения в столбик

Деление периодических дробей

Этот метод по существу тот же, что и в Ведической математике, когда они используют «вертикальную и поперечную» сутру при умножении двухзначных чисел. Стиль уравнения - единственная реальная разница. В Ведической математике уравнение записывается на двух строках, как показано ниже. Для прямого метода уравнение находится на одной линии с ответом под мультипликацией.

Вы можете посмотреть видео о прямом умножении с использованием двухзначных множителей или продолжить чтение следующих примеров. Количество начальных нулей всегда совпадает с числом цифр в множителе, поэтому при умножении на 2-значные числа мы всегда добавляем 2 старших нуля. Следующее: мы умножаем две единичные цифры вместе.

Внимательно просмотрите и примените в своих действиях!

Какие ошибки при умножении
можно сделать и
как их избежать

Внимательно просмотрите,

чтобы не совершать ошибок!

Правила для других случаев умножения

Умножение в столбик на однозначное число

Этот шаг включает в себя умножение десятков цифр одного числа на цифру единиц другой. При написании уравнения на одной строке, если мы рисуем изогнутые соединительные линии между умноженными цифрами, мы получаем внешнюю пару и внутреннюю пару. При написании уравнения на двух строках мы получаем крест, когда рисуем прямые соединительные линии между умноженными цифрами.

Умножение в столбик двух многозначных натуральных чисел

Добавляя результаты этих двух уравнений, получим 14, поэтому мы пишем 4 и переносим. На этом шаге мы умножаем десятки цифр каждого числа. При написании уравнения на одной строке внешняя пара на этом шаге соединяется с нулем, поэтому результат этой пары равен нулю и может быть проигнорирован. В этом примере умственные вычисления, которые нам нужно сделать, относительно просты, и поскольку мы делаем меньше шагов, чем традиционный метод умножения, это происходит быстрее. Однако есть недостаток такого подхода, особенно когда участвующие цифры больше.

Этот пример можно записать в столбик.

Под числом 34 записываем число 2 по правилу:

Под числом 68 записываем число 2 по правилу:

Мы умножаем две единичные цифры вместе. Итак, мы пишем 2 и нести. Это то, где это становится жестким, особенно если вы пытаетесь мысленно выполнить расчет. Итак, мы пишем 4 и нести. У нас есть 63, к которым мы добавляем перенос 14, чтобы дать нам. Запишем 7 и нести.

Как умножать в столбик: основные правила

Следуя оригинальному методу и причине ведущих нулей, у нас есть дополнительный шаг из-за переноса. Итак, мы имеем нуль плюс перенос 7, который мы записываем 7, который дает нам наш ответ. Этот шаг может показаться излишним, и мы могли бы просто записать перенос на последнем шаге, но по мере изучения метода лучше следовать всему уравнению до тех пор, пока вы не будете достаточно знакомы с методом, чтобы взять небольшие ярлыки.

Единицы записываем под единицами, а десятки, если они будут под десятками

1 Умножать начинаем с единиц.

2 умножим на 8. Получится 16.

  • 16 единиц – это 1 десяток и 6 единиц.
  • 6 единиц пишем под единицами. А 1 десяток запомним и прибавим к десяткам.

Теперь 2 умножим на 6 десятков. Получится 12.

12 десятков да ещё 1 всего 13 десятков.

Как вы можете видеть, когда цифры содержат цифры 7, 8 и 9, математика становится более сложной, особенно если вы пытаетесь сделать это мысленно. Яков также понял это, и он поставил себе задачу найти более простой способ добиться этого. Введите метод «двух пальцев», как он это называл, что упрощает вычисления, которые вам нужно выполнить. Прежде чем перейти к методу с двумя пальцами, нам нужно получить дополнительную справочную информацию для одноразрядного умножения.

Примеры умножения многозначного числа на однозначное число

При умножении двух цифр на одну цифру результат может быть только одним или двумя цифрами. Если мы ставим нуль перед результатом любой цифры, мы можем обрабатывать все результаты умножения двух чисел с одной цифрой в виде двухзначных результатов, цифры единиц и десятки цифр.

  • 13 десятков – это 1 сотня да ещё 3 десятка.
  • 3 десятка пишу под десятками. А 1 сотню запомним и прибавим к сотням.

Сотен в этом примере нет, поэтому сразу на месте сотен напишем 1.

Читаем ответ : 68 умножить на 2 получится 136.