Главная / Освещение

Как решать дробные пропорции. Составить пропорцию

Для решения большинства задач в математике средней школы необходимо знание по составлению пропорций. Это несложное умение поможет не только выполнять сложные упражнения из учебника, но и углубиться в саму суть математической науки. Как составить пропорцию? Сейчас разберем.

Самым простым примером является задача, где известны три параметра, а четвертый необходимо найти. Пропорции бывают, конечно, разные, но часто требуется найти по процентам какое-нибудь число. Например, всего у мальчика было десять яблок. Четвертую часть он подарил своей маме. Сколько осталось яблок у мальчика? Это самый простой пример, который позволит составить пропорцию. Главное это сделать. Изначально было десять яблок. Пусть это 100%. Это мы обозначили все его яблоки. Он отдал одну четвертую часть. 1/4=25/100. Значит, у него осталось: 100% (было изначально) - 25% (он отдал) = 75%. Эта цифра показывает процентное отношение количества оставшихся фруктов к количеству имевшихся сначала. Теперь у нас есть три числа, по которым уже можно решить пропорцию. 10 яблок - 100%, х яблок - 75%, где х - искомое количество фруктов. Как составить пропорцию? Необходимо понимать, что это такое. Математически это выглядит так. Знак равно поставлен для вашего понимания.

10 яблок = 100%;

x яблок = 75%.

Оказывается, что 10/x = 100%/75. Это и есть основное свойство пропорций. Ведь чем больше x, тем больше процентов составляет это число от исходного. Решаем эту пропорцию и получаем, что x=7,5 яблок. Почему мальчик решил отдать нецелое количество, нам неизвестно. Теперь вы знаете, как составить пропорцию. Главное, найти два соотношения, в одном из которых есть искомое неизвестное.

Решение пропорции часто сводится к простому умножению, а потом к делению. В школах детям не объясняют, почему это именно так. Хотя важно понимать, что пропорциональные отношения есть математическая классика, сама суть науки. Для решения пропорций необходимо уметь обращаться с дробями. Например, часто приходится переводить проценты в обыкновенные дроби. То есть запись 95% не подойдет. А если сразу написать 95/100, то можно провести солидные сокращения, не начиная основного подсчета. Сразу стоит сказать, что если ваша пропорция получилась с двумя неизвестными, то ее не решить. Никакой профессор вам здесь не поможет. А ваша задача, скорее всего, имеет более сложный алгоритм правильных действий.

Рассмотрим еще один пример, где нет процентов. Автомобилист купил 5 литров бензина за 150 рублей. Он подумал о том, сколько он бы заплатил за 30 литров топлива. Для решения этой задачи обозначим за x искомое количество денег. Можете самостоятельно решить эту задачу и потом проверить ответ. Если вы еще не поняли, как составить пропорцию, то смотрите. 5 литров бензина - это 150 рублей. Как и в первом примере, запишем 5л - 150р. Теперь найдем третье число. Конечно, это 30 литров. Согласитесь, что пара 30 л - х рублей уместна в данной ситуации. Перейдем на математический язык.

5 литров - 150 рублей;

30 литров - х рублей;

Решаем эту пропорцию:

x = 900 рублей.

Вот и решили. В своей задаче не забудьте проверить на адекватность ответ. Бывает, что при неправильном решении автомобили достигают нереальных скоростей в 5000 километров в час и так далее. Теперь вы знаете, как составить пропорцию. Также вы сможете ее решить. Как видите, в этом нет ничего сложного.

Решение задачи с помощью пропорции сводится к тому, чтобы сделать неизвестное значение x членом этой пропорции. Затем используя основное свойство пропорции получить линейное уравнение и решить его.

Предварительные навыки Содержание урока

Как решить задачу с помощью пропорции

Рассмотрим простейший пример. Трем группам нужно выплатить стипендию по 1600 рублей каждому. В первой группе 20 студентов. Значит первой группе будет выплачено 1600 × 20, то есть 32 тыс. рублей.

Во второй группе 17 человек. Значит второй группе будет выплачено 1600 × 17, то есть 27,200 тыс. руб.

Ну и выплатим стипендию третьей группе. В ней 15 человек. На них нужно затратить 1600 × 15, то есть 24 тыс. руб.

В результате имеем следующее решение:

Для подобных задач решение можно записывать с помощью пропорции.

Пропорция по определению есть равенство двух отношений. К примеру, равенство является пропорцией. Эту пропорцию можно прочесть следующим образом:

a так относится к b , как c относится d

Аналогично можно соотнести стипендию и студентов, так чтобы каждому досталось по 1600 рублей.

Итак, запишем первое отношение, а именно отношение тысячи шестисот рублей на одного человека:

Мы выяснили, что для выплаты 20 студентам по 1600 рублей, нам потребуется 32 тыс. рублей. Значит второе отношение будет отношением тридцати двух тысяч к двадцати студентам:

Теперь соединим полученные отношения знаком равенства:

Мы получили пропорцию. Её можно прочесть следующим образом:

Тысяча шестьсот рублей так относятся к одному студенту, как тридцать две тысячи рублей относятся к двадцати студентам .

Понимай по 1600 рублей каждому. Если выполнить деление в обеих частях равенства , то обнаружим, что одному студенту, как и двадцати студентам достанется по 1600 рублей.

Теперь представим, что сумма денег, необходимых для выплаты стипендии двадцати студентам, была бы неизвестной. Скажем, если бы вопрос стоял так: в группе 20 студентов и каждому нужно выплатить по 1600 рублей. Сколько всего рублей требуется для выплаты стипендии?

В таком случае пропорция приняла бы вид . То есть, сумма денег, необходимая для выплаты стипендии, стала неизвестным членом пропорции. Эту пропорцию можно прочесть так:

Тысяча шестьсот рублей так относятся к одному студенту, как неизвестное число рублей относится к двадцати студентам

Теперь воспользуемся основным свойством пропорции. Оно гласит, что произведение крайних членов пропорции равно произведению средних:

Перемножив члены пропорции «крест-накрест», получим равенство 1600 × 20 = 1 × x . Вычислив обе части равенства, получим 32000 = x или x = 32000 . Иными словами, мы найдём значение неизвестной величины, которую искали.

Аналогично можно было определить общую сумму и для остального количества студентов — для 17 и 15. Эти пропорции выглядели как и . Воспользовавшись основным свойством пропорции, можно найти значение x

Задача 2 . Расстояние равное 100 км автобус проехал за 2 часа. Сколько времени потребуется автобусу, чтобы проехать 300 км, если будет ехать с той же скоростью?

Можно сначала определить расстояние, которое автобус проезжает за один час. Затем определить сколько раз это расстояние содержится в 300 километрах:

100: 2 = 50 км на каждый час движения

300 км: 50 = 6 часов

Либо можно составить пропорцию «сто километров так относятся к одному часу, как триста километров к неизвестному числу часов»:

Отношение одноименных величин

Если крайние или средние члены пропорции поменять местами, то пропорция не нарушится.

Так, в пропорции можно поменять местами крайние члены. Тогда получится пропорция .

Пропорция также не нарушится, если её перевернуть, то есть использовать обратные отношения в обеих частях.

Перевернем пропорцию . Тогда получим пропорцию . Взаимосвязь при этом не нарушается. Отношение между студентами равно отношению между суммами денег, предназначенных для этих студентов. Такую пропорцию часто составляют в школе, когда для решения задачи составляются таблицы

Этот способ записи очень удобен, поскольку позволяет перевести условие задачи в более понятный вид. Решим задачу в которой требовалось определить сколько рублей нужно для выплаты стипендии двадцати студентам.

Условие задачи запишем следующим образом:

Составим таблицу на основе этого условия:

Составим пропорцию, используя данные таблицы:

Используя основное свойство пропорции, получим линейное уравнение и найдем его корень:

Изначально, мы имели дело с пропорцией , которая составлена из отношений величин разной природы. В числителях отношений располагались суммы денег, а в знаменателях количество студентов:

Поменяв местами крайние члены, мы получили пропорцию . Эта пропорция составлена из отношений величин одной природы. В первом отношении содержатся количества студентов, а во втором — суммы денег:

Если отношение составлено из величин одной природы, то мы будем называть его отношением одноименных величин . Например, отношения между фруктами, деньгами, физическими величинами, явлениями, действиями.

Отношение может быть составлено, как из одноименных величин, так и из величин разной природы. Примерами последних являются отношение расстояния ко времени, отношения стоимости товара к его количеству, отношение общей суммы стипендии к количеству студентов.

Пример 2 . В школьном саду посажены сосны и березы, причём на каждую сосну приходится 2 березы. Сколько посадили сосен в саду, если берез посадили 240?

Определим сколько сосен было посажено в саду. Для этого составим пропорцию. В условии сказано, что на каждую сосну приходится 2 березы. Напишем отношение, показывающее что на одну сосну приходится две березы:

Теперь напишем второе отношение, показывающее что на x сосен приходится 240 берез

Соединим эти отношения знаком равенства, получим следующую пропорцию:

«2 березы так относятся к одной сосне,
как 240 берез относятся к x соснам»

Используя основное свойство пропорции, находим значение x

Либо пропорцию можно составить, предварительно записав условие, как в прошлом примере:

Получится та же пропорция, но в этот раз она будет составлена из отношений одноименных величин:

Значит в саду посадили 120 сосен.

Пример 3 . Из 225 кг руды получили 34,2 кг меди. Каково процентное содержание меди в руде?

Можно разделить 34,2 на 225 и полученный результат выразить в процентах:

Либо составить пропорцию 225 килограммам руды так приходятся на 100%, как 34,2 кг меди приходятся на неизвестное число процентов:

Либо составить пропорцию в которой отношения составлены из одноименных величин:

Задачи на прямую пропорциональность

Понимание отношений одноименных величин приводит к пониманию решения задач на прямую и обратную пропорциональность. Начнем с задач на прямую пропорциональность.

Для начала вспомним, что такое прямая пропорциональность. Это взаимосвязь между двумя величинами при которой увеличение одной из них влечет за собой увеличение другой во столько же раз.

Если расстояние в 50 км автобус прошел за 1 час, то для прохождения расстояния в 100 км (при той же скорости) автобусу потребуется 2 часа. Во сколько раз увеличилось расстояние, во столько же раз увеличилось время движения. Как показать это с помощью пропорции?

Одно из предназначений отношения заключается в том, чтобы показать во сколько раз первая величина больше второй. А значит и мы c помощью пропорции можем показать, что расстояние и время увеличились в два раза. Для этого воспользуемся отношением одноименных величин.

Покажем, что расстояние увеличилось в два раза:

Аналогично покажем, что время увеличилось во столько же раз

«100 километров так относятся к 50 километрам, как 2 часа относятся к 1 часу»

Если выполнить деление в обеих частях равенства , то обнаружим что расстояние и время были увеличены в одинаковое число раз.

2 = 2

Задача 2 . За 3 ч на мельнице смололи 27 т пшеничной муки. Сколько тонн пшеничной муки можно смолоть за 9 ч, если темп работы не изменится?

Решение

Время работы мельницы и масса перемолотой муки — прямо пропорциональные величины. При увеличении времени работы в несколько раз, количество перемолотой муки увеличится во столько же раз. Покажем это с помощью пропорции.

В задаче дано 3 ч. Эти 3 ч увеличились до 9 ч. Запишем отношение 9 ч к 3 ч. Это отношение будет показывать во сколько раз увеличилось время работы мельницы:

Теперь запишем второе отношение. Это будет отношение x тонн пшеничной муки к 27 тоннам. Данное отношение будет показывать, что количество перемолотой муки увеличилось во столько же раз, сколько и время работы мельницы

Соединим эти отношения знаком равенства, получим пропорцию .

Воспользуемся основным свойством пропорции и найдем x

Значит за 9 ч можно смолоть 81 т пшеничной муки.

Вообще, если взять две прямо пропорциональные величины и увеличить их в одинаковое число раз, то отношение нового значения к старому значению первой величины будет равно отношению нового значения к старому значению второй величины.

Так и в предыдущей задаче старые значения были 3 ч и 27 т. Эти значения были увеличены в одинаковое число раз (в три раза). Новыми значениями стали 9 ч и 81 ч. Тогда отношение нового значения времени работы мельницы к старому значению равно отношению нового значения массы перемолотой муки к старому значению

Если выполнить деление в обеих частях равенства, то обнаружим, что время работы мельницы и количество смолотой муки увеличилось в одинаковое число раз:

3 = 3

Пропорцию, которую составляют к задачам на прямую пропорциональность, можно описать с помощью выражения:

Где впоследствии стало равно 81.

Задача 2 . Для 8 коров в зимнее время доярка ежедневно заготовляет 80 кг сена, 96 кг корнеплодов, 120 кг силоса и 12 кг концентратов. Определить ежедневный расход этих кормов для 18 коров.

Решение

Количество коров и масса каждого из кормов — прямо пропорциональные величины. При увеличении количества коров в несколько раз, масса каждого из кормов увеличится во столько же раз.

Составим несколько пропорций, вычисляющих массу каждого из кормов для 18 коров.

Начнем с сена. Ежедневно для 8 коров его заготовляют 80 кг. Тогда для 18 коров будет заготовлено x кг сена.

Запишем отношение, показывающее во сколько раз увеличилось количество коров:

Теперь запишем отношение, показывающее во сколько раз увеличилась масса сена:

Соединим эти отношения знаком равенства, получим пропорцию:

Отсюда находим x

Значит для 18 коров нужно заготовить 180 кг сена. Аналогично определяем массу корнеплодов, силоса и концентратов.

Для 8 коров ежедневно заготовляют 96 кг корнеплодов. Тогда для 18 коров будет заготовлено x кг корнеплодов. Составим пропорцию из отношений и , затем вычислим значение x

Определим сколько силоса и концентратов нужно заготовить для 18 коров:

Значит для 18 коров ежедневно нужно заготавливать 180 кг сена, 216 кг корнеплодов, 270 кг силоса и 27 кг концентратов.

Задача 3 . Хозяйка варит вишнёвое варенье, причём на 3 стакана вишни кладёт 2 стакана сахара. Сколько сахара нужно положить на 12 стаканов вишни? на 10 стаканов вишни? на стакана вишни?

Решение

Количество стаканов вишни и количество стаканов сахарного песка — прямо пропорциональные величины. При увеличении количества стаканов вишни в несколько раз, количество стаканов сахара увеличится во столько же раз.

Запишем отношение, показывающее во сколько раз увеличилось количество стаканов вишни:

Теперь запишем отношение, показывающее во сколько раз увеличилось количество стаканов сахара:

Соединим эти отношения знаком равенства, получим пропорцию и найдем значение x

Значит на 12 стаканов вишни нужно положить 8 стаканов сахара.

Определим количество стаканов сахара для 10 стаканов вишни и стакана вишни

Задачи на обратную пропорциональность

Для решения задач на обратную пропорциональность опять же можно использовать пропорцию, составленнаю из отношений одноименных величин.

В отличие от прямой пропорциональности, где величины увеличиваются или уменьшаются в одну и ту же сторону, в обратной пропорциональности величины изменяются обратно друг другу.

Если одна величина увеличивается в несколько раз, то другая уменьшается во столько же раз. И наоборот, если одна величина уменьшается в несколько раз, то другая увеличивается во столько же раз.

Допустим, что нужно покрасить забор, состоящий из 8 листов

Один маляр будет красить все 8 листов сам

Если маляров будет 2, то каждый покрасит по 4 листа.

Это конечно же при условии, что маляры будут честными между собой и справедливо разделят эту работу поровну на двоих.

Если маляров будет 4, то каждый покрасит по 2 листа

Замечаем, что при увеличении количества маляров в несколько раз, количество листов которые приходятся на одного маляра уменьшаются во столько же раз.

Итак, мы увеличили количество маляров с 1 до 4. Другими словами, увеличили количество маляров в четыре раза. Запишем это с помощью отношения:

В результате количество листов забора, которые приходятся на одного маляра уменьшилось в четыре раза. Запишем это с помощью отношения:

Соединим эти отношения знаком равенства, получим пропорцию

«4 маляра так относятся к 1 маляру, как 8 листов относятся к 2 листам»

Задача 2 . 15 рабочих закончили отделку квартир в новом доме за 24 дня. За сколько дней выполнили бы эту работу 18 рабочих?

Решение

Количество рабочих и количество дней, затраченных на работу — обратно пропорциональные величины. При увеличении количества рабочих в несколько раз, количество дней, необходимых для выполнения этой работы, уменьшится во столько же раз.

Запишем отношение 18 рабочих к 15 рабочим. Это отношение будет показывать во сколько раз увеличилось количество рабочих

Теперь запишем второе отношение, показывающее во сколько раз уменьшилось количество дней. Поскольку количество дней уменьшится с 24 дней до x дней, то второе отношение будет отношением старого количества дней (24 дня) к новому количеству дней (x дней)

Соединим полученные отношения знаком равенства, получим пропорцию:

Отсюда находим x

Значит 18 рабочих выполнят необходимую работу за 20 дней.

Вообще, если взять две обратно пропорциональные величины и увеличить одну из них в определенное число раз, то другая уменьшится во столько же раз. Тогда отношение нового значения к старому значению первой величины будет равно отношению старого значения к новому значению второй величины.

Так и в предыдущей задаче старые значения были 15 рабочих и 24 дня. Количество рабочих было увеличено с 15 до 18 (т.е. было увеличено в раза). В результате количество дней, необходимых для выполнения работы, уменьшилось во столько же раз. Новыми значениями стали 18 рабочих и 20 дней. Тогда отношение нового количества рабочих к старому количеству равно отношению старого количества дней к новому количеству

Для составления пропорции к задачам на обратную пропорциональность можно пользоваться формулой:

Применительно к нашей задаче значения переменных будут следующими:

Где впоследствии стало равно 20.

Задача 2 . Скорость парохода относится к скорости течения реки, как 36: 5. Пароход двигался вниз по течению 5 ч 10 мин. Сколько времени потребуется ему, чтобы вернуться обратно?

Решение

Собственная скорость парохода составляет 36 км/ч. Скорость течения реки реки 5 км/ч. Поскольку пароход двигался по течению руки, то скорость его движения составила 36 + 5 = 41 км/ч. Время пути составила 5 ч 10 мин. Для удобства выразим время в минутах:

5 ч 10 мин = 300 мин + 10 мин = 310 мин

Поскольку на обратном пути пароход двигался против течения реки, то его скорость составила 36 − 5 = 31 км/ч.

Скорость парохода и время его движения — обратно пропорциональные величины. При уменьшении скорости в несколько раз, время его движения увеличится во столько же раз.

Запишем отношение, показывающее во сколько раз уменьшилась скорость движения:

Теперь запишем второе отношение, показывающее во сколько раз увеличилось время движения. Поскольку новое время x будет больше старого времени, в числителе отношения запишем время x , а в знаменателе старое время, равное трёхсот десяти минутам

Соединим полученные отношения знаком равенства, получим пропорцию . Отсюда найдём значение x

410 минут это 6 часов и 50 минут. Значит пароходу потребуется 6 часов и 50 минут, чтобы вернуться обратно.

Задача 3 . На ремонте дороги работало 15 человек, и они должны были закончить работу за 12 дней. На пятый день утром подошли еще несколько рабочих, и оставшаяся работа была выполнена за 6 дней. Сколько рабочих прибыло дополнительно?

Решение

Вычтем из 12 дней 4 отработанных дня. Так мы определим сколько ещё дней осталось работать пятнадцати рабочим

12 дней − 4 дня = 8 дней

На пятый день дополнительно прибыло x рабочих. Тогда всего рабочих стало 15 + x .

Количество рабочих и количество дней, необходимых для выполнения работы — обратно пропорциональные величины. При увеличении количества рабочих в несколько раз, количество дней уменьшится во столько же раз.

Запишем отношение, показывающее во сколько раз увеличилось количество рабочих:

Теперь запишем во сколько раз уменьшилось количество дней, необходимых для выполнения работы:

Соединим эти отношения знаком равенства, получим пропорцию . Отсюда можно вычислить значение x

Значит 5 рабочих прибыло дополнительно.

Масштаб

Масштабом называют отношение длины отрезка на изображении к длине соответствующего отрезка на местности.

Допустим, что расстояние от дома до школы составляет 8 км. Попробуем нарисовать план местности, где будут указаны дом, школа и расстояние между ними. Но изобразить на бумаге расстояние, равное 8 км мы не можем, поскольку оно довольно велико. Но зато мы можем уменьшить это расстояние в несколько раз так, чтобы оно уместилось на бумаге.

Пусть километры на местности на нашем плане будут выражаться в сантиметрах. Переведем 8 километров в сантиметры, получим 800 000 сантиметров.

Уменьшим 800 000 см в сто тысяч раз:

800 000 см: 100 000 см = 8 см

8 см это расстояние от дома до школы, уменьшенное в сто тысяч раз. Теперь без труда можно нарисовать на бумаге дом и школу, расстояние между которыми будет 8 см.

Эти 8 см относятся к реальным 800 000 см. Так и запишем с помощью отношения:

8: 800 000

Одно из свойств отношения гласит, что отношение не меняется если его члены умножить или разделить на одно и то же число.

В целях упрощения отношения 8: 800 000 оба его члена можно разделить на 8. Тогда получим отношение 1: 100 000. Это отношение и назовём масштабом. Данное отношение показывает, что один сантиметр на плане относится (или соответствует) ста тысячам сантиметров на местности.

Поэтому на нашем рисунке необходимо указать, что план составлен в масштабе 1: 100 000

1 см на плане относится к 100 000 см на местности;
2 см на плане относится к 200000 см на местности;
3 см на плане относится к 300000 на местности и т.д.

К любой карте или плану указывается в каком масштабе они сделаны. Этот масштаб позволяет определять реальное расстояние между объектами.

Так, наш план составлен в масштабе 1: 100 000. На этом плане расстояние между домом и школой составляет 8 см. Чтобы вычислить реальное расстояние между домом и школой, нужно 8 см увеличить в 100 000 раз. Иными словами, умножить 8 см на 100 000

8 см × 100 000 = 800 000 см

Получаем 800 000 см или 8 км, если перевести сантиметры в километры.

Допустим, что между домом и школой располагается дерево. На плане расстояние между школой и этим деревом составляет 4 см.

Тогда реальное расстояние между домом и деревом будет 4 см × 100 000 = 400 000 см или 4 км.

Расстояние на местности можно определять с помощью пропорции. В нашем примере расстояние между домом и школой будет вычисляться с помощью следующей пропорции:

1 см на плане так относится к 100000 см на местности, как 8 см на плане относятся к x см на местности.

Из этой пропорции узнаём, что значение x равно 800000 см.

Пример 2 . На карте расстояние между двумя городами составляет 8,5 см. Определить реальное расстояние между городами, если карта составлена в масштабе 1: 1 000 000.

Решение

Масштаб 1: 1 000 000 указывает, что 1 см на карте соответствует 1 000 000 см на местности. Тогда 8,5 см будут соответствовать x см на местности. Составим пропорцию 1 к 1000000 как 8,5 к x

В 1 км содержится 100000 см. Тогда в 8 500 000 см будет

Либо можно рассуждать так. Расстояние на карте и расстояние на местности — прямо пропорциональные величины. При увеличении расстояния на карте в несколько раз, расстояние на местности увеличится во столько же раз. Тогда пропорция примет следующий вид. Первое отношение будет показывать во сколько раз расстояние на местности больше расстояния на карте:

Второе отношение покажет, что расстояние на местности во столько же раз больше, чем 8,5 см на карте:

Отсюда x равен 8 500 000 см или 85 км.

Задача 3 . Длина реки Невы 74 км. Чему равняется ее длина на карте, масштаб которой 1: 2 000 000

Решение

Масштаб 1: 2000000 говорит о том, что 1 см на карте соответствует 2 000 000 см на местности.

А 74 км на это 74 × 100 000 = 7 400 000 см на местности. Уменьшив 7 400 000 в 2 000 000, мы определим длину реки Невы на карте

7 400 000: 2 000 000 = 3,7 см

Значит на карте, масштаб которой 1: 2 000 000 длина реки Невы составляет 3,7 см.

Запишем решение с помощью пропорции. Первое отношение будет показывать сколько раз длина на карте меньше длины на местности:

Второе отношение будет показывать, что 74 км (7 400 000 см) уменьшились во столько же раз:

Отсюда находим x равный 3,7 см

Задачи для самостоятельного решения

Задача 1. Из 21 кг хлопкового семени получили 5,1 кг масла. Сколько масла получится из 7 кг хлопкового семени?

Решение

Пусть x кг масла можно получить из 7 кг хлопкового семени. Масса хлопкового семени и масса получаемого масла — прямо пропорциональные величины. Тогда уменьшение хлопкового семени с 21 кг до 7 кг, приведет к уменьшению получаемого масла во столько же раз.

Ответ: из 7 кг хлопкового семени получится 1,7 кг масла.

Задача 2. На некотором участке железнодорожного пути старые рельсы длиной в 8 м заменили новыми длиной в 12 м. Сколько потребуется новых двенадцатиметровых рельсов, если сняли 360 старых рельсов?

Решение

Длина участка на котором производится замена рельсов равна 8 × 360 = 2880 м.

Пусть x двенадцатиметровых рельсов требуется для замены. Увеличение длины одного рельса с 8 м до 12 м приведет к уменьшению количества рельсов с 360 до x штук. Иными словами, длина рельса и их количество связаны обратно пропорциональной зависимостью

Ответ: для замены старых рельсов потребуется 240 новых.

Задача 3. 60% учеников класса пошли в кино, а остальные 12 человек – на выставку. Сколько учащихся в классе?

Решение

Если 60% учащихся пошли в кино, а остальные 12 человек на выставку, то на 40% учащихся и будут приходиться 12 человек, пошедших на выставку. Тогда можно составить пропорцию в которой 12 учащихся так относятся к 40%, как все x учащихся относятся к 100%

Либо можно составить пропорцию, состоящей из отношений одноименных величин. Количество учащихся и процентная доля изменяются прямо пропорционально. Тогда можно записать, что во сколько раз увеличилось количество участников во столько же раз увеличилась процентная доля

Задача 5. Пешеход затратил на путь 2,5 ч, двигаясь со скоростью 3,6 км/ч. Сколько времени затратит пешеход на тот же путь, если его скорость будет 4,5 км/ч

Решение

Скорость и время — обратно пропорциональные величины. При увеличении скорости в несколько раз, время движения уменьшится во столько же раз.

Запишем отношение, показывающее по сколько раз увеличилась скорость движения пешехода:

Запишем отношение, показывающее что время движения уменьшилось во столько же раз:

Соединим эти отношения знаком равенства, получим пропорцию и найдём значение x

Либо можно воспользоваться отношениями одноименных величин. Количество выпущенных станков и процентная доля, на которые эти станки приходятся, связаны прямо пропорциональной зависимостью. При увеличении количества станков в несколько раз, процентная доля увеличивается во столько же раз. Тогда можно записать, что 230 станков во столько раз больше, чем x станков, во сколько раз больше 115%, чем 100%

Ответ: по плану завод должен был выпустить 200 станков.

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Пропо́рция – равенство двух отношений, т. е. равенство вида a: b = c: d , или, в других обозначениях, равенство

Если a : b = c : d , то a и d называют крайними , а b и c - средними членами пропорции.

От « пропорции» никуда не деться, без нее не обойтись во многих задачах. Выход только один – разобраться с этим отношением и пользоваться пропорцией как палочкой-выручалочкой.

Прежде чем приступать к рассмотрению задач на пропорцию, важно вспомнить основное правило пропорции:

В пропорции

произведение крайних членов равно произведению средних

Если какая-то величина в пропорции неизвестна, ее легко будет найти, опираясь на это правило.

Например,

То есть неизвестная величина пропорции – значении дроби, в знаменателе которой – то число, которое стоит напротив неизвестной величины , в числителе – произведение оставшихся членов пропорции (независимо от того, где эта неизвестная величина стоит ).

Задача 1.

Из 21 кг хлопкового семени получили 5,1 кг масла. Сколько масла получится из 7 кг хлопкового семени?

Решение:

Мы понимаем, что уменьшение веса семени во сколько-то раз, влечет за собой уменьшение веса получаемого масла во столько же раз. То есть величины связаны прямой зависимостью.

Заполним таблицу:

Неизвестная величина – значение дроби , в знаменателе которой – 21 – величина, стоящая напротив неизвестного в таблице, в числителе – произведение оставшихся членов таблицы-пропорции.

Поэтому получаем, что из 7 кг семени выйдет 1,7 кг масла.

Чтобы правильно заполнять таблицу, важно помнить правило:

Одинаковые наименования нужно записывать друг под другом. Проценты записываем под процентами, килограммы под килограммами и т.д

Задача 2.

Перевести в радианы.

Решение:

Мы знаем, что . Заполним таблицу:

Задача 3.

На клетчатой бумаге изображён круг. Какова площадь круга, если площадь заштрихованного сектора равна 27?

Решение:

Хорошо видно, что незаштрихованный сектор соответствует углу в (например, потому, что стороны сектора образованы биссектрисами двух смежных прямых углов). А поскольку вся окружность составляет , то на закрашенный сектор приходится .

Составим таблицу:

Откуда площадь круга – есть .

Задача 4. После того, как было вспахано 82% всего поля, осталось вспахать еще 9 га. Какова площадь всего поля?

Решение:

Все поле составляет 100%, и поскольку вспахано 82%, то осталось вспахать 100%-82%=18% поля.

Заполняем таблицу:

Откуда получаем, что все поле составляет (га).

А следующая задача – с засадой.

Задача 5.

Расстояние между двумя городами пассажирский поезд прошел со скоростью 80км/ч за 3 часа. За сколько часов товарный поезд пройдет то же расстояние со скоростью 60 км/ч ?

Если вы будете решать эту задачу аналогично предыдущей, то получите следующее:

время, которое потребуется товарному поезду, чтобы пройти то же расстояние, что и пассажирским, есть часа. То есть, получается, что идя с меньшей скоростью, он преодолевает (за одно и тоже время) расстояние быстрее, нежели поезд с большей скоростью.

В чем ошибка рассуждений?

До сих пор мы рассматривали задачи, где величины были прямопропорциональны друг другу , то есть рост одной величины во сколько-то раз, дает рост связанной с ней второй величины во столько же раз (аналогично с уменьшением, конечно). А здесь у нас другая ситуация: скорость пассажирского поезда больше скорости товарного во сколько-то раз, а вот время, требуемое на преодоление одного и того же расстояния, требуется пассажирскому поезду меньшее во столько же раз, нежели товарному поезду. То есть величины друг другу обратно пропорциональны .

Схему, которой мы пользовались до сих пор, надо чуть изменить в данном случае.

Решение:

Рассуждаем так:

Пассажирский поезд со скоростью 80 км/ч ехал 3 ч, следовательно, он проехал км. А значит товарный поезд это же расстояние преодолеет за ч.

То есть, если бы мы составляли пропорцию, нам следовало бы поменять местами ячейки правой колонки предварительно. Получили бы: ч.

Поэтому, пожалуйста, будьте внимательны при составлении пропорции. Разберитесь сначала, с какой зависимостью имеете дело – с прямой или обратной.

Пропорция в переводе с латинского языка (proportio) означает соотношение, выравненность частей, то есть равенство двух отношений. Умение вычислять пропорции часто бывает необходимым в бытовых ситуациях.

Спонсор размещения P&G Статьи по теме "Как посчитать пропорцию" Как складывать квадратные корни Как найти диагональ квадрата Как найти координаты вершины параболы

Простой пример, когда необходимо применить знания о решении пропорций: как вычислить 13% от вашей заработной платы – те самые проценты, которые уходят в Пенсионный фонд.

Напишите две строчки пропорции. В первой укажите общую сумму зарплаты, которая представляет собой 100%, то есть, например, 15 000 (рублей) = 100%.

Строчкой ниже обозначьте ту сумму, которую нужно вычислить, знаком «Х», который равен 13%, то есть Х = 13%.

Основное свойство пропорции звучит так: произведение крайних членов пропорции равно произведению её средних членов. Это значит, что если вы помножите 15 000 на 13, то полученное число будет равняться значению Х, помноженному на 100. То есть перемножая члены пропорции крест накрест, вы получите одинаковое значение.

Чтобы вычислить, чему равен в конечном итоге Х, умножьте 15 000 на 13 и разделите на 100. У вас получится, что 13 процентов от вашей зарплаты составляет 1950 рублей, таким образом, на руки вы получаете 15 000 – 1950 = 13 050 рублей чистой зарплаты.

Если вам нужно взять для пирога 100 граммов сахарной пудры, а вы знаете, что в одном граненом стакане помещается 140 граммов, составьте следующую пропорцию:

Подсчитайте, чему равен Х.

Х = 100 х 1 / 140 = 0,7

То есть вам понадобится 0,7 стакана сахарной пудры.

Бывает, что нужно вычислить целое, зная только процентную часть. Например, вы знаете, что 21 человек на предприятии, а это 5% от общего количества сотрудников, имеют среднее специальное образование. Составьте пропорцию, чтобы вычислить общее количество сотрудников: Х (человек) = 100%, 21 = 5%. 21 х 100 / 5 = 420 человек.

Таким образом, записав в две строки имеющиеся данные, значение неизвестного члена нужно находить так: помножьте между собой те члены пропорции, которые оказываются рядом и сверху неизвестного и разделите полученное число на значение, которое находится по диагонали от неизвестного.

А = Б х С / Д; Б = А х Д / С; С = А х Д / Б; Д = С х Б / А

В геометрии существует несколько видов диагоналей. Диагональю называется отрезок, который соединяет две не соседние (не принадлежащие одной стороне или одному ребру) вершины многоугольника или многогранника. Различают так же диагонали граней, рассматриваемых как многоугольники и пространственные

Куб представляет собой частный случай параллелепипеда, в котором каждая из граней образована правильным многоугольником - квадратом. Всего куб обладает шестью гранями. Вычислить площадь не представляет затруднений. Спонсор размещения P&G Статьи по теме "Как вычислить площадь куба" Как складывать

Что представляет собой пропорция? С математической точки зрения, пропорция – это равенство двух отношений. Все части пропорции являются взаимозависимыми, а их результат неизменен. Вам понадобится - Учебник алгебры за 7 класс. Спонсор размещения P&G Статьи по теме "Как вычислить пропорцию" Как

Часто в жизни приходится применять простые математические действия быстро и без помощи электронных вычислителей. К примеру, при подсчете заработной платы надо вычесть от общей денежной суммы тринадцать процентов. Как это сделать? Ведь вычитать разные виды чисел нельзя, без определенного

Всё познается в сравнении. Отношение некоторых величин друг к другу можно выразить в процентах. Например, посчитав, какой процент жидкости от основной массы содержится в 1 кг помидоров и огурцов, вы узнаете, что будет сочнее. Вам понадобится 1) Бумага 2) Ручка 3) Калькулятор Спонсор размещения

Среднее арифметическое - важное понятие, используемое во многих разделах математики и ее приложениях: статистике, теории вероятностей, экономике и.т.д. Среднее арифметическое можно определить как общее понятие средней величины. Спонсор размещения P&G Статьи по теме "Как вычислить среднее

Умение решать пропорции может пригодиться и в повседневной жизни. Допустим, у вас на кухне уксусная эссенция с содержанием 40% уксуса, а вам нужен 6% уксус. Без составления пропорции тут никак не обойтись. Вам понадобится ручка, листок бумаги, аналитическое мышление Спонсор размещения P&G Статьи по

От необходимости сложных математических расчетов у обычного человека кругом идет голова. Попробуйте-ка подсчитать, какова сумма подоходного налога от вашей зарплаты. В этом случае вам поможет простое действие - составление пропорции. Пропорция - это равенство двух частных. Записывается она в виде

В математике пропорцией называют равенство двух отношений. Для всех ее частей характерна взаимозависимость и неизменный результат. Достаточно рассмотреть один пример, чтобы понять принцип решения пропорций. Спонсор размещения P&G Статьи по теме "Как найти пропорцию" Как вычесть процент от суммы Как

Уже с первого класса малыши узнают на уроках математики такие понятия, как равенство, знаки «больше» и «меньше». С годами задания становятся все сложней, но требование составить равенство встречается в них также достаточно часто, поскольку знак «равно» - основа любых преобразований в математике.

Как составить пропорцию? Поймет любой школьник и взрослый

5 литров - 150 рублей;

30 литров - х рублей;

Решаем эту пропорцию:

Как найти процент от числа

Чтобы найти процент от числа, например, 35% от 1000 рублей, нужно оно же Откуда взялась цифра 100? Из самого определения. Процент - это сотая доля числа.

На калькуляторе можно 1000 умножить на 35 и нажать на кнопку %

Как найти 100 процентов

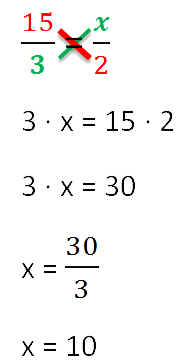
Например, мы знаем, что 350 рублей составляет 35%. Сколько же будет 100%?

Процент между двумя числами

Какую часть одно число составляет от другого. Например, на сколько процентов был выполнен план, если предполагался доход 800 рублей, а в итоге получили 1040 рублей.

Онлайн калькулятор расчёта процентов

Не обязательно в расчёт брать 100%. Например, посещаемость с Яндекса, Гугл, ВКонтакте и т.д. составляет 100%. С Яндекса на сайт приходит 800 посетителей, что составляет 67% от общего числа. А с Гугол - 55 посетителей. Какой процент посетителей приходит с Google?

Как посчитать на сколько процентов одно число меньше другого

Зарплата понизилась с 1040 рублей до 800 рублей. На сколько процентов уменьшилась зарплата? На сколько процентов 800 меньше 1040? Неизвестная 800.

Как узнать на сколько процентов одно число больше другого

Зарплата повысилась с 800 до 1040 рублей. На сколько процентов увеличилась зарплата? На сколько процентов 1040 больше 800? Неизвестная 1040.

Пишем пропорцию можно вывести формулу

Увеличение числа на указанный процент

Число b больше 800 на 30%. Нужно вычислить число b.

Пишем пропорцию можно вывести формулу

Пример: сумма без НДС равна 1000 рублей. Сколько будет общая сумма с НДС 18%

Уменьшение числа на заданный процент

Число a меньше 1040 на 23%. Чему равен a?

Пишем пропорцию можно вывести формулу

Скрипт для веб-разработчиков

JavaScript очень прост (выделила математические действия в теге form): input - поле, куда вводим значения

output - область с результатом

parseFloat(g3.value) или g3.valueAsNumber - преобразует строку в число

235 комментариев:

Ничерта не нужна (есть калькулятор в телефоне), но иногда может случиться так, что придётся делать скрипт расчёта стоимости натяжного потолка. NMitra А как же банковский процент, скажем, на кредит или вклад? Или процент переходов с поиска? Или налоги для ИП?

Итого: 20% Анонимный Мне надо 20% настойка прополиса. Купила в аптеке настойку,но в инструкции и на бутылочке надпись:настойка - 1:10 == Как сделать 20% ? NMitra Не берусь вам дать совет. У меня нет медицинского образования. Анонимный Я еще со школы терпеть не могу все,что связано с цифрами,вычислениями.И как ни странно,учусь на финансиста,а самых элементарных арифметических действий не знаю.И когда я слышу слово "задачи",мне аж не по себе становится. NMitra:)) Анонимный УНС УНС УНС УНС! Анонимный все равно не понятно. или я тупая или. незнаю:(А(мишка)***хД*** Задачу решить не могу:((Анонимный 1:10 это часть взрослой дозы для детей. если во флаконе 25 мл, то умножайте 1 мл - это 25 капель - 25*25 (если разжиженное) и дальше рассчитывайте проценты. а так от многих факторов зависит сколько капель на мл. (состояние густоты, размер пипетки и т.д.). Анонимный Привет, а как узнать разницу между двумя числами в %. Т.е. на сколько одно число больше второго.

например 950000 от 87000

бОльшее брать за 100%? тогда цифра получается 91.58, это получается 8.42%. Правильно я считаю? Спасибо Анонимный Блин не верно написал 95000 и 87000 NMitra Хотя, нет я не правильно поняла вопрос.

NMitra Приятно слышать, что твоя работа оценена, пожалуйста Nasiba Как быть если сумма процента известна а сам процент нет. Например 3000 основная сумма 1400 каким процентом этой суммы является? NMitra 3000 - 100%

NMitra Бывает. Анонимный Вкладчик внес 3500 руб под 15% годовых, какую сумму он получит через 3 года? NMitra Проценты начисляются или причисляются? Если причисляются, то в какой срок (раз в три месяца, раз в шесть месяцев)?

525*3=1575 (за три) Анонимный беру кредит на 5 000 000 рублей под 20% на 12 месяцев, сколько я должна платить в месяц?Напишите расчет пожалуйста. Спасибо. NMitra Проценты годовые или месячные?

* на оплату процентов,

* списание основного долга.

* аннуитетный платеж при котором сумма ежемесячных выплат одинаковая (в вашем случае около 463 172,53 рублей),

* дифференцированный платёж при котором списывается одинаковая сумма основного долга (в вашем случае 5 000 000 / 12 = 416 666,67):

365 - количество дней в году

Проценты: 5 000 000 * 0,2 * 30 / 365 = 82 191,78

Платёж: 416 666,67 + 82 191,78 = 498 858,45

Проценты: 4 583 333,33 * 0,2 * 31 / 365 = 77 853,88

Платёж: 416 666,67 + 77 853,88 = 494 520,55

Проценты: 5 000 000 * 0,2 = 1 000 000

Платёж: 416 666,67 + 1 000 000 = 1 416 666,67

Остаток: 5 000 000 - 416 666,67 = 4 583 333,33

Проценты: 4 583 333,33 * 0,2 = 916 666,66

Платёж: 416 666,67 + 916 666,66 = 1 333 333,33

Остаток: 4 583 333,33 - 416 666,67 = 4 166 666,66

Огромное спасибо! Анонимный скажите пожалуйста.как вычесть процент от выручки.по какой формуле? NMitra Выручка 1000 рублей, процент, который нужно вычесть 35%

1000*0,35=350 рублей (это процент от выручки, см. первая форма)

1000 - 350 = 650 рублей (в выручке осталось 650 рублей) Анонимный Влажность воздуха 97%. Уменьшаем на 1%. Какая сьанет влажность воздуза помле этого? NMitra 96% насколько я понимаю. Анонимный сумма3395 из этой 0,33% в день NMitra 3395*0,33=11.2035 Анонимный вместо 1600 осталось 1200 на сколько процентов сократилось NMitra Пропорция:

С = 2,2*B = 2.2 * A / 0,44 = 5

х% составляет 1000

х = 100000/4600 = 21,73913 (тот, кто дал 1000€)

21,73913 составляет х

х = 14500*21,73913/100 = 3152,17 (тот, кто дал 1000€)

3600*100:9900=37%, но это процент от 1000

100%-37%=63%, это процент от 3600

ваша сумма=63% (это 6237 евро) + вложенное 3600=9837

моя=37% (это 3663 евро) + 1000=4663 евро. Анонимный Как им доказать..что не правы..получается их сумма увеличилась в 4.5 раза..хотя общая сумма-в три с хвостиком. не хочется ругаться из-за денег. NMitra Вы из конечной суммы вычитаете первоначальный капитал. Предположим.

А она (см. комментарий 64):

21,73913% (тот, кто дал 1000€)

78,26087% (тот, кто дал 3600€)

1000 из 4600 - это 1/4,6 от суммы (4600/4,6=1000).

1/4 - это 25%, 1/4,6 - это (100/4,6=21,73913%)

По идее нужно решать через пропорцию 7*100/0, на на 0 делить нельзя. Меня это ставит в тупик! NMitra Согласна с вами, вопрос поставлен не корректно, на ноль делить нельзя, можно лишь на бесконечно малую функцию. Анонимный Так как же пример решить? Вроде простая задачка из начальной школы, но взорвала умы всех моих знакомых, кому в районе тридцати))) NMitra Вопрос имел бы смысл, если бы звучал так: "На сколько в правой руке у него больше яблок, чем в левой?"

7 - 0 = 7 Ответ: на 7 яблок. Может опечатка? Анонимный Ладно. Рассказываю как есть. Мой муж на работе следит за нарушениями. В первом квартале их не было. Во втором зафиксировано 7. Данные нужно подать в виде процентного соотношения: на сколько процентов во втором квартале нарушений больше. Если бы было 4 и 5, соответственно, то решить не сложно.

NMitra Ничего не получается, бесконечность ((

во втором 7 нарушений, что соответствует х

или 1000 * 1,12 = 1120

91 год - 20129,03 тыс.руб

92 год - 39686,42 тыс. руб

абсолютное изменение - 19557,39 тыс.руб

NMitra А что искали? Даже на глаз видно, что 20 меньше 40 на половину (50%), а именно

х=19557,39*100/39686,42=49,28 Анонимный Как вычесляется сумма если: 1000*1.2^12=8916. NMitra ^ - это символ степени https://ru.wikipedia.org/wiki/%C2%EE%E7%E2%E5%E4%E5%ED%E8%E5_%E2_%F1%F2%E5%EF%E5%ED%FC#.D0.97.D0.BD.D0.B0.D1.87.D0.BE.D0.BA_.D1.81.D1.82.D0.B5.D0.BF.D0.B5.D0.BD.D0.B8

8,916100448 * 1000 = 8916,100448

В первом случае у нас на депозите будет 1000*1.2^3=1728, т.е. почти 73% рост за три месяца.

Что же будет со вторым вкладом, а здесь та же формула: 1000*1.2^12=8916руб.

Получаем почти 800% прибыли или рост депозита почти в 9 раз за один год.

Конкретно меня интерисует эта формула, как вообще она работает или как ростет процент прибыли.

То есть проценты причисляются к общей сумме. Анонимный Здравствуйте,

Спасибо за отличный сайт и за вычисления процентов. Только я не смог здесь найти" обратное вычисление". Например есть число: 1045, из него я хочу взять 600 (для дальнейших действий). Вопрос: эти 600, это сколько процентов от 1045 ? И где тот волшебный калькулятор на котором это можно подсчитать? 1045/100=10.45 - это один процент. Затем 10.45*на 600 ? Получается чушь! =6270. Это что? Что это за бяка?

Спасибо. NMitra Анонимный,

х = 100000*5/100 = 5000 Анонимный Здравствуйте, NMitra.

Подскажите пожалуйста как посчитана себестоимость 4,3 млн. руб, а то у меня не сходится ничего:

оборот 6 млн. руб в месяц, средняя наценка составляет 39%, следовательно себестоимость продукции – 4,3 млн.

NMitra 4,3 + 4,3 * 39 / 100 = 6

Себестоимость = О/(1 + Н/100) = 6 / (1 + 39 / 100)

Я думала, что наценка считается таким способом:

Это неправильно же? Тогда что я могла посчитать таким способом? NMitra 6*39/100 - это 39 процентов от 6

6 - 2,34 - это 61 процент от 6

Анонимный Да, мне нужно от оборота было вычесть 39% наценки, чтобы получить себестоимость без наценки.

Спасибо большое еще раз! Анонимный Объясните пожалуйста на сколько меньше если в 2013 году вывезли 2800 товаров, а в 2014 вывезли 2400 товаров, за 100% брать всегда 2014 год.

На 14,3% в 2014 вывезли меньше? NMitra У меня также получается. Анонимный Спасибо Анонимный А в случае увеличения, если суммы те же, то получится также - 14,3% NMitra Нет, цифра будет другая Анонимный А почему? NMitra Чтобы разобраться, сформулируйте задачу и предложите её решение. Без примеров труднее объяснить, а так вы и сами сейчас поймёте в чём разница. Анонимный Подскажите пожалуйста как рассчитать проценты по французской и германской системе начисления процентов,

если дата выдачи кредита 22 апреля 2014 года, а дата возврата 16 сентября, ставка по кредиту 16% годовых.

S = s * (1 + P/100 * d/D)

Процентная ставка (P) = 16

Количество дней в году (D) = 365 дней или 366 (високосный год) дней

Количество дней (d) = 8 апрель + 31 май + 30 июнь + 31 июль + 31 август + 16 сентябрь = 147 дней

Количество дней в году (D) = 360 дней

Количество дней (d) = 8 апрель + 30 май + 30 июнь + 30 июль + 30 август + 16 сентябрь = 144 дней Анонимный NMitra! Спасибо Вам, выручили. Анонимный Здравствуйте! помогите вычислить процент за кредит

В банке хотим взять кредит, дают 440.000 / оплата 11.722 в месяц на 60 месяцев

NMitra Здравствуйте, платёж постоянный на протяжении всего срока или уменьшается с уменьшением основного долга? Проценты месячные или годовые? Я бы ориентировалась не на процент (какое-то число, например 20%), а на конечную сумму, которую вы отдадите банку помимо основного долга со всеми дополнительными комиссиями, в том числе единовременными:

703320 - 440000 = 263320 (из них процентов)

263320/5 = 52664 (процентов в год)

Анонимный Здравствуйте! 40 000 под 9.20% сколько будет начислино проценты через месяц? NMitra 40000*0,092=3680

Но! Проценты у вас скорее всего годовые, поэтому эту сумму вы получите по прошествии года.

А эта сумма за месяц. Но не точно, так как обычно считается не количество месяцев, а количество дней, в течении которого пролежит вклад. В разных месяцах разное количество дней.

ЕСЛИ Я ПРАВИЛЬНО СЧИТАЮ ТО ПОЛУЧАЕТСЯ: 344*100/30984 = 1,11 NMitra Верно думаете. Анонимный Уровень обращаемости населения за медицинской помощью в 2013 году составило 121681 обращение, в 2014-118480

Исходя из данных, как найти процент снижение количество вызовов?

верно будет такое решение 121681-118480=3201*100/121681= NMitra 121681 - 100%

х = 118480*100/121681 = 97,37%

Анонимный 65651651 Анонимный помогите

в 2001 выручка возросла по сравнению 2000 на 2 процента хотя планировали в 2 раза на сколько процентов не довыпольнин план NMitra 2 раза - это 200%

200% - 2% = 198% (на 198% недовыполнен план) Анонимный помогите

в 2 полугодие произвели детали на 0.5 % по сравнению с первым полугодия план производства быль не довыпольнин на 16.5% на сколько %планировались изменит производства уменьшения или повишения Анонимный помогите ответить на вопрос. Арбуз содержит 99% влажность, но после усушки (положить на солнышко на несколько дней) влажность его составляет 98%, НА СКОЛЬКО % ИЗМЕНИТСЯ ВЕС АРБУЗА ПОСЛЕ УСУШКИ? огромное спасибо NMitra Про производство: некорректно сформулирована задача

"в 2 полугодие произвели детали на 0.5 % по сравнению с первым полугодия" - больше или меньше?

х = 40% Анонимный у меня гола лопается, но в реальности он же не может терять половину веса.Это значит что математический расчет не совпадает с реальностью. Летом буду проводить эксперимент с арбузом:)))))) СПасибо NMitra Соотношение влажности и веса может идти по гиперболе (см. графики элементарных функций) Сергей Рыскин Помогите решить задачу, от какого числа отняли 20% чтоб получилось 600

Сергей Рыскин Методом подбора я понял, что это 750, мне нужно чтоб так считало в еxsel ? для этого нужна формула, вопрос в формуле, как она пишется

NMitra 20% = 20/100 = 0,2

итоговая сумма: 12901,00 или

Объясните мне, если можно. NMitra Итоговая сумма неверно рассчитана:)

А если 11740,4 умножить на 130% что мы получим? NMitra Правильно формулируйте вопросы:

Хорошо, все равно Я не понял.

(Пример: Есть прайс-лист- три колонки цен

оптовая-(1006,00), розница+35% к опт (1358,00), интернет+25% к опт (1258,00).

Есть розничная цена - 16772,00

хотим дать скидку -30% от суммы

Почему нельзя разделить на 130% NMitra 1006 (опт)

1006 + 352.1 = 1358,1 (розн 35%)

1358,1 * 0,35 = 475.335

1358,1 - 475,335 = 882,765

Опт = Розн/(1 + процент/100) = 1358,1/(1 + 35/100) = 1358,1 / 1,35 = 1006

х = 50*100/1100 = 4,55% (процент скидки от розн. в перерасчёте на опт.) Анонимный Огромное спасибо! russYliusha Ребята всем привет. очень нужна помощь. Допустим мой друг брал кредит в банк 15000€ на пять лет (60 месяцев) он платит в месяц по 270€ в течение пять лет в итоге выходит 16200€ , Вопрос:

Как узнать Процентную ставку банка, то есть сколько процентов берет банк.

СПАСИБО. NMitra 16200 - 15000 = 1200 (за 5 лет)

1200 / 5 = 240 (за год)

х% = 240*100/15000 = 1,6% (годовая ставка)

15000 / 60 = 250 (основной долг в месяц)

А вы не могли бы мне сказать формулу в excel ! Или как это все считать в excel!!Спасибо большое!! NMitra У меня не более знаний, чем давали в школе в моё время. Подставляйте известные

Ребята как узнать сколько мне платят в час?

Работал 80 часов а получил 1000 € ,

За ранее спасибо!! NMitra 1 - x

x = 1000 / 80 = 12,5 € (в час) maksimovgenya Доброго времени суток.

из них испорченных книг 4.

х = 100*4/113 = 3,54% Анонимный Нужно найти,сколько процентов составляет 500 000 от 32 000 000,заранее благодарю Анонимный На счету есть 2500 евро, которые положили на 3 месяца под 4%. По истечению 3х месяцев на счету оказалось 2570 евро. Правильно ли я считаю, что 4 % от 2500 это 100 евро, т.е. окончательная сумма по истечению срока должна быть 2600 евро. Но оператор сказала что так "тупо" проценты считать нельзя. Как в этом случае происходит расчет? NMitra 32 000 000 - 100%

x = 500 000 * 100 / 32 000 000 = 50 / 32 = 1.5625% (полтора процента) NMitra Комментарий 158: проценты во всех случаях рассчитываются одинаково. Оператор обязана объяснить вам как именно происходит расчёт (какое количество дней, какие берутся комиссии и т.д.)!

Указанных вами данных мне не хватает:

1) как правило, процент указывается годовой (так процент выглядит более внушительно), а у вас сразу за три месяца?

2) прошло полных три месяца после открытия счёта?

3) банк не берёт разовых комиссий при открытии/закрытии счёта?

Понятие "маржа" имеет разное значение, у коллег по цеху поинтересуйтесь, что именно они имеют ввиду. NMitra Маржа в % — отношение разницы между ценой и себестоимостью к цене = (Цена - Себестоимость) * 100 / Цена

Полная себестоимость = 900

х - 600 = 400 / 100 * 600 = 2400

х = 2400 + 600 = 3000

0.5 куб. камеры ___ X ?? watt

1.0 куб. камеры ___ 2948 watt NMitra 0,5 - это половина, но в задаче какая-то другая закономерность, не проценты

2552,18 + 382.827 = 2935

z1 - конечное значение диапазона

х = (37-22)*100/(63-22) = 1500 / 41 = 37%

2 3 4 5 6 7 8 9 10 11 12 Evgeniya Nikolskaya Помогите пожалуйста) к закупочной цене прибавили 15% получилась продажная цена. Сколько отнять процентов от продажной цены, чтобы получилась закупочная цена. NMitra См. комментарий 95

NMitra 500 * 0,05 = 25 Анонимный подскажите пожалуйста общий транспортный расход 3700 привезли на одной машине два товара стоимостью один товар 2200 а второй 27800 как считать их транспортный расход NMitra всего 2200+27800=30000 (это 100%)

х = 2200*3700/30000 = 271

х = 27800*3700/30000 = 3429 Анонимный NMitra

А как же банковский процент, скажем, на кредит или вклад? Или процент переходов с поиска? Или налоги для ИП?

x = (568 - 1,2y)/0,8 = 710 - 1,5y

y = 650 - 710 + 1,5y = -60 + 1,5y

х = 42*23/94 = 10 Артур Нечипурук О-о, вы уже отписались.

Благо голова ещё не насколько отупела, чтобы не решить это самостоятельно, вспомнил, достал тетрадь и вывел самостоятельно нужную здесь пропорцию.. (надо хоть изредка упражняться)

NMitra Умножить число на 10101:) Артур Нечипурук Вчера ещё разобрался, читал объяснения:) Анонимный было 165 стало 230 на сколько % увелчился объем продаж? NMitra 230-165=65

х = 65*100/165=39 (на 39%) Анонимный Вопрос на автостоянке стояле легковые и грузовые машины легковые машины больше на 1,15 раза на сколько процентов легковых машин больше чем грузовых

Процентный калькулятор: 7 основных операций с процентами

Результат расчета

Результат расчета

Результат расчета

Результат расчета

Результат расчета

Результат расчета

Результат расчета

Результат расчета

Результат расчета

Один процент - это сотая часть от числа. Данное понятие используется, когда нужно обозначить отношение доли к целому. Кроме этого, в процентах можно сравнивать несколько величин, при этом обязательно указывая, относительного какого целого проценты вычисляются. Например, расходы выше доходов на 10 % или цена на железнодорожные билеты возросла на 15 % в сравнении с тарифами прошлого года. Число процентов выше 100 означает, что доля превышает целое, как часто бывает при статистических расчетах.

Процент как финансовое понятие - плата, заемщика кредитору за предоставление денег во временное пользование. В бизнесе встречается выражение «работать за проценты». В данном случае подразумевается, что размер вознаграждения зависит от прибыли или оборота (комиссионные). Обойтись без вычисления процентов невозможно в бухгалтерии, бизнесе, банковском деле. Чтобы упростить расчеты, разработан онлайн-калькулятор процентов.

Калькулятор позволяет вычислить:

Процент от заданного значения.
Процент из суммы (налог по фактической зарплате).
Процент от разницы (НДС из суммы с НДС).

При решении задач на калькуляторе процентов нужно оперировать тремя значениями, одно из которых неизвестно (по заданным параметрам вычисляется переменная). Сценарий расчета следует выбирать, исходя из заданных условий.

Примеры расчетов

1. Вычисление процента от числа

Чтобы найти число, составляющее 25 % от 1 000 руб., нужно:

Для расчета на обычном калькуляторе, нужно 1 000 умножить на 25 и нажать кнопку %.

2. Определение целого числа (100 %)

Мы знаем, что 250 руб. составляет 25 % от какого-то числа. Как его вычислить?

Составим простую пропорцию:

3. Процент между двумя числами

Допустим, предполагалась прибыль 800 руб., а получили 1 040 руб. Каков процент превышения?

Пропорция будет такой:

Перевыполнения плана по прибыли - 30 %, то есть выполнение - 130 %.

4. Расчет не из 100 %

Например, в магазин, состоящий из трех отделов, приходят 100 % покупателей. В продуктовый отдел - 800 человек (67 %), в отдел бытовой химии - 55. Какой процент покупателей приходит в отдел бытовой химии?

5. На сколько процентов одно число меньше другого

Цена товара упала с 2 000 до 1 200 руб. На сколько процентов подешевел товар или на сколько процентов 1 200 меньше 2 000?

2 000 - 100 %
1 200 – Y %
Y = 1 200 × 100 / 2 000 = 60 % (60 % к цифре 1 200 от 2 000)
100 % − 60 % = 40 % (число 1 200 меньше 2 000 на 40 %)

6. На сколько процентов одно число больше другого

Зарплата выросла с 5 000 до 7 500 рублей. На сколько процентов увеличилась зарплата? На сколько процентов 7 500 больше 5 000?

5 000 руб. - 100 %
7 500 руб. - Y %
Y = 7 500 × 100 / 5 000 = 150 % (в цифре 7 500 150 % от 5 000)
150 % − 100 % = 50 % (число 7 500 больше 5 000 на 50 %)

7. Увеличение числа на определенный процент

Цена товара S выше 1 000 руб. на 27 %. Какова цена товара?

Онлайн-калькулятор делает вычисления намного проще: вам нужно выбрать вид расчета, ввести число и процент (в случае вычисления процентного соотношения - второе число), указать точность расчета и дать команду о начале действий.

Как посчитать (высчитать) процент от суммы?

Как посчитать процент от суммы , требуется знать во многих случаях (при расчете госпошлины, кредита и т. п.). Мы расскажем, как посчитать проценты от суммы с помощью калькулятора, пропорций и известных соотношений.

Как узнать процент от суммы в общем случае?

После этого есть два варианта:

Если нужно узнать, сколько процентов составляет другая сумма от первоначальной, нужно просто разделить ее на размер 1%, полученный ранее.
Если же нужен размер суммы, которая составляет, скажем, 27,5% от первоначальной, нужно размер 1% умножить на требуемое количество процентов.

Как высчитать процент из суммы с помощью пропорции?

Но можно поступить и иначе. Для этого придется использовать знания о методе пропорций, который проходят в рамках школьного курса математики. Это будет выглядеть так.

Пусть у нас есть А — основная сумма, равная 100%, и В — сумма, соотношение которой с А в процентах нам нужно узнать. Записываем пропорцию:

(Х в данном случае — число процентов).

По правилам расчета пропорций мы получаем следующую формулу:

Если же нужно узнать, сколько будет составлять сумма В при уже известном числе процентов от суммы А, формула будет выглядеть по-другому:

Теперь остается подставить в формулу известные числа — и можно производить расчет.

Как рассчитать процент от суммы с помощью известных соотношений?

Наконец, можно воспользоваться и более простым способом. Для этого достаточно помнить, что 1% в виде десятичной дроби — это 0,01. Соответственно, 20% — это 0,2; 48% — 0,48; 37,5% — это 0,375 и т. д. Достаточно умножить исходную сумму на соответствующее число — и результат будет означать размер процентов.

Кроме того, иногда можно воспользоваться и простыми дробями. Например, 10% — это 0,1, то есть 1/10 следовательно, узнать, сколько составят 10%, просто: нужно всего лишь разделить исходную сумму на 10.

Другими примерами таких соотношений будут:

12,5% — 1/8, то есть нужно делить на 8;
20% — 1/5, то есть нужно разделить на 5;
25% — 1/4, то есть делим на 4;
50% — 1/2, то есть нужно разделить пополам;
75% — 3/4, то есть нужно разделить на 4 и умножить на 3.

Правда, не все простые дроби удобны для расчета процентов. К примеру, 1/3 близка по размерам к 33%, но не равна точно: 1/3 — это 33,(3)% (то есть дробь с бесконечными тройками после запятой).

Как вычесть процент от суммы без помощи калькулятора

Если же требуется от уже известной суммы отнять неизвестное число, составляющее какое-то количество процентов, можно воспользоваться следующими методами:

Вычислить неизвестное число с помощью одного из приведенных выше способов, после чего отнять его от исходного.
Сразу рассчитать остающуюся сумму. Для этого от 100% отнимаем то число процентов, которое нужно вычесть, и полученный результат переводим из процентов в число любым из описанных выше способов.

Второй пример удобнее, поэтому проиллюстрируем его. Допустим, надо узнать, сколько останется, если от 4779 отнять 16%. Расчет будет таким:

Отнимаем от 100 (общее количество процентов) 16. Получаем 84.
Считаем, сколько составит 84% от 4779. Получаем 4014,36.

Как высчитать (отнять) из суммы процент с калькулятором в руках

Все вышеприведенные вычисления проще делать, используя калькулятор. Он может быть как в виде отдельного устройства, так и в виде специальной программы на компьютере, смартфоне или обычном мобильнике (даже самые старые из ныне используемых устройств обычно имеют эту функцию). С их помощью вопрос, как высчитать процент из суммы, решается очень просто:

Набирается исходная сумма.
Нажимается знак «-».
Вводится число процентов, которое требуется вычесть.
Нажимается знак «%».
Нажимается знак «=».

В итоге на экране высвечивается искомое число.

Как отнять от суммы процент с помощью онлайн-калькулятора

Наконец, сейчас в сети достаточно сайтов, где реализована функция онлайн-калькулятора. В этом случае даже не требуется знания того, как посчитать процент от суммы : все операции пользователя сводятся к вводу в окошки нужных цифр (или передвижению ползунков для их получения), после чего результат сразу высвечивается на экране.

Особенно эта функция удобна тем, кто рассчитывает не просто абстрактный процент, а конкретный размер налогового вычета или сумму госпошлины. Дело в том, что в этом случае вычисления сложнее: требуется не только найти проценты, но и прибавить к ним постоянную часть суммы. Онлайн-калькулятор позволяет избежать подобных добавочных вычислений. Главное — выбрать сайт, пользующийся данными, которые соответствуют действующему закону.

С точки зрения математики, пропорцией является равенство двух отношений. Взаимозависимость характерна для всех частей пропорции, также как и их неизменный результат. Понять, как составить пропорцию можно, ознакомившись со свойствами и формулой пропорции. Чтобы разобраться с принципом решения пропорции, достаточным будет рассмотреть один пример. Только непосредственно решая пропорции, можно легко и быстро обучиться этим навыкам. А данная статья поможет читателю в этом.

Свойства пропорции и формула

Обращение пропорции. В случае, когда заданное равенство выглядит как 1a: 2b =3c: 4d, записывают 2b: 1a = 4d: 3c. (Причем 1a, 2b, 3c и 4d являются простыми числами, отличными от 0).
Перемножение заданных членов пропорции крест-накрест. В буквенном выражении это имеет такой вид: 1a: 2b = 3c: 4d, а запись 1a4d = 2b3c будет ему равносильна. Таким образом, произведение крайних частей любой пропорции (числа по краям равенства) всегда является равным произведению средних частей (чисел, расположенных посредине равенства).
При составлении пропорции может пригодиться и такое её свойство, как перестановка крайних и средних членов. Формулу равенства 1a: 2b = 3c: 4d, можно отобразить такими вариантами:
- 1a: 3c = 2b: 4d (когда переставляют средние члены пропорции).
- 4d: 2b = 3c: 1a (когда переставляют крайние члены пропорции).
Прекрасно помогает в решении пропорции её свойство увеличения и уменьшения. При 1a: 2b = 3c: 4d, записывают:
- (1a + 2b) : 2b = (3c + 4d) : 4d (равенство по увеличению пропорции).
- (1a – 2b) : 2b = (3c – 4d) : 4d (равенство по уменьшению пропорции).
Составить пропорцию можно сложением и вычитанием. Когда пропорция записана как 1a: 2b = 3c: 4d, тогда:
- (1a + 3с) : (2b + 4d) = 1a: 2b = 3c: 4d (пропорция составлена сложением).
- (1a – 3с) : (2b – 4d) = 1a: 2b = 3c: 4d (пропорция составлена вычитанием).
Также, при решении пропорции, содержащей дробные или большие числа, можно разделить или умножить оба её члена на одинаковое число. К примеру, составные части пропорции 70:40=320:60, можно записать так: 10*(7:4=32:6).
Вариант решения пропорции с процентами выглядит так. К примеру, записывают, 30=100%, 12=x. Теперь следует перемножить средние члены (12*100) и разделить на известный крайний (30). Таким образом, получается ответ: x=40%. Подобным способом можно при необходимости совершать перемножение известных крайних членов и делить их на заданное среднее число, получая искомый результат.

Если Вас интересует конкретная формула пропорции, то в самом простом и распространенном варианте пропорция представляет собой такое равенство (формулу): a/b = c/d, в нем a, b, c и d являются отличными от нуля четырьмя числами.