Методы кластерного анализа. Задачи кластеризации в Data Mining

Кластерный анализ

Большинство исследователей склоняются к тому, что впервые термин «кластерный анализ» (англ. cluster - гроздь, сгусток, пучок) был предложен математиком Р.Трионом . Впоследствии возник ряд терминов, которые в настоящее время принято считать синонимами термина «кластерный анализ»: автоматическая классификация; ботриология.

Кластерный анализ - это многомерная статистическая процедура, выполняющая сбор данных, содержащих информацию о выборке объектов, и затем упорядочивающая объекты в сравнительно однородные группы (кластеры)(Q-кластеризация, или Q-техника, собственно кластерный анализ). Кластер - группа элементов, характеризуемых общим свойством, главная цель кластерного анализа - нахождение групп схожих объектов в выборке. Спектр применений кластерного анализа очень широк: его используют в археологии, медицине, психологии, химии, биологии, государственном управлении, филологии, антропологии, маркетинге, социологии и других дисциплинах. Однако универсальность применения привела к появлению большого количества несовместимых терминов, методов и подходов, затрудняющих однозначное использование и непротиворечивую интерпретацию кластерного анализа. Орлов А. И. предлагает различать следующим образом:

Задачи и условия

Кластерный анализ выполняет следующие основные задачи :

• Разработка типологии или классификации.
• Исследование полезных концептуальных схем группирования объектов.
• Порождение гипотез на основе исследования данных.
• Проверка гипотез или исследования для определения, действительно ли типы (группы), выделенные тем или иным способом, присутствуют в имеющихся данных.

Независимо от предмета изучения применение кластерного анализа предполагает следующие этапы :

• Отбор выборки для кластеризации. Подразумевается, что имеет смысл кластеризовать только количественные данные.
• Определение множества переменных, по которым будут оцениваться объекты в выборке, то есть признакового пространства.
• Вычисление значений той или иной меры сходства (или различия) между объектами.
• Применение метода кластерного анализа для создания групп сходных объектов.
• Проверка достоверности результатов кластерного решения.

Кластерный анализ предъявляет следующие требования к данным :

1. показатели не должны коррелировать между собой;
2. показатели не должны противоречить теории измерений;
3. распределение показателей должно быть близко к нормальному;
4. показатели должны отвечать требованию «устойчивости», под которой понимается отсутствие влияния на их значения случайных факторов;
5. выборка должна быть однородна, не содержать «выбросов».

Можно встретить описание двух фундаментальных требований предъявляемых к данным - однородность и полнота:

Однородность требует, чтобы все сущности, представленные в таблице, были одной природы. Требование полноты состоит в том, чтобы множества I и J представляли полную опись проявлений рассматриваемого явления. Если рассматривается таблица в которой I - совокупность, а J - множество переменных, описывающих эту совокупность, то должно должно быть представительной выборкой из изучаемой совокупности, а система характеристик J должна давать удовлетворительное векторное представление индивидов i с точки зрения исследователя .

Если кластерному анализу предшествует факторный анализ , то выборка не нуждается в «ремонте» - изложенные требования выполняются автоматически самой процедурой факторного моделирования (есть ещё одно достоинство - z-стандартизация без негативных последствий для выборки; если её проводить непосредственно для кластерного анализа, она может повлечь за собой уменьшение чёткости разделения групп). В противном случае выборку нужно корректировать.

Типология задач кластеризации

Типы входных данных

В современной науке применяется несколько алгоритмов обработки входных данных. Анализ путём сравнения объектов, исходя из признаков, (наиболее распространённый в биологических науках) называется Q -типом анализа, а в случае сравнения признаков, на основе объектов - R -типом анализа. Существуют попытки использования гибридных типов анализа (например, RQ -анализ), но данная методология ещё должным образом не разработана.

Цели кластеризации

• Понимание данных путём выявления кластерной структуры. Разбиение выборки на группы схожих объектов позволяет упростить дальнейшую обработку данных и принятия решений, применяя к каждому кластеру свой метод анализа (стратегия «разделяй и властвуй »).
• Сжатие данных . Если исходная выборка избыточно большая, то можно сократить её, оставив по одному наиболее типичному представителю от каждого кластера.
• Обнаружение новизны (англ. novelty detection ). Выделяются нетипичные объекты, которые не удаётся присоединить ни к одному из кластеров.

В первом случае число кластеров стараются сделать поменьше. Во втором случае важнее обеспечить высокую степень сходства объектов внутри каждого кластера, а кластеров может быть сколько угодно. В третьем случае наибольший интерес представляют отдельные объекты, не вписывающиеся ни в один из кластеров.

Во всех этих случаях может применяться иерархическая кластеризация , когда крупные кластеры дробятся на более мелкие, те в свою очередь дробятся ещё мельче, и т. д. Такие задачи называются задачами таксономии . Результатом таксономии является древообразная иерархическая структура. При этом каждый объект характеризуется перечислением всех кластеров, которым он принадлежит, обычно от крупного к мелкому.

Методы кластеризации

Общепринятой классификации методов кластеризации не существует, но можно отметить солидную попытку В. С. Берикова и Г. С. Лбова . Если обобщить различные классификации методов кластеризации, то можно выделить ряд групп (некоторые методы можно отнести сразу к нескольким группам и потому предлагается рассматривать данную типизацию как некоторое приближение к реальной классификации методов кластеризации):

1. Вероятностный подход . Предполагается, что каждый рассматриваемый объект относится к одному из k классов. Некоторые авторы (например, А. И. Орлов) считают, что данная группа вовсе не относится к кластеризации и противопоставляют её под названием «дискриминация», то есть выбор отнесения объектов к одной из известных групп (обучающих выборок).
2. Подходы на основе систем искусственного интеллекта . Весьма условная группа, так как методов AI очень много и методически они весьма различны.
3. Логический подход . Построение дендрограммы осуществляется с помощью дерева решений.
4. Теоретико-графовый подход .
   • Графовые алгоритмы кластеризации
5. Иерархический подход . Предполагается наличие вложенных групп (кластеров различного порядка). Алгоритмы в свою очередь подразделяются на агломеративные (объединительные) и дивизивные (разделяющие). По количеству признаков иногда выделяют монотетические и политетические методы классификации.
   • Иерархическая дивизивная кластеризация или таксономия. Задачи кластеризации рассматриваются в количественной таксономии.
6. Другие методы . Не вошедшие в предыдущие группы.
   • Статистические алгоритмы кластеризации
   • Ансамбль кластеризаторов
   • Алгоритмы семейства KRAB
   • Алгоритм, основанный на методе просеивания
   • DBSCAN и др.

Подходы 4 и 5 иногда объединяют под названием структурного или геометрического подхода, обладающего большей формализованностью понятия близости . Несмотря на значительные различия между перечисленными методами все они опираются на исходную «гипотезу компактности »: в пространстве объектов все близкие объекты должны относиться к одному кластеру, а все различные объекты соответственно должны находиться в различных кластерах.

Формальная постановка задачи кластеризации

Пусть - множество объектов, - множество номеров (имён, меток) кластеров. Задана функция расстояния между объектами . Имеется конечная обучающая выборка объектов . Требуется разбить выборку на непересекающиеся подмножества, называемые кластерами , так, чтобы каждый кластер состоял из объектов, близких по метрике , а объекты разных кластеров существенно отличались. При этом каждому объекту приписывается номер кластера .

Алгоритм кластеризации - это функция , которая любому объекту ставит в соответствие номер кластера . Множество в некоторых случаях известно заранее, однако чаще ставится задача определить оптимальное число кластеров, с точки зрения того или иного критерия качества кластеризации.

Кластеризация (обучение без учителя) отличается от классификации (обучения с учителем) тем, что метки исходных объектов изначально не заданы, и даже может быть неизвестно само множество .

Решение задачи кластеризации принципиально неоднозначно, и тому есть несколько причин (как считает ряд авторов):

• не существует однозначно наилучшего критерия качества кластеризации. Известен целый ряд эвристических критериев, а также ряд алгоритмов, не имеющих чётко выраженного критерия, но осуществляющих достаточно разумную кластеризацию «по построению». Все они могут давать разные результаты. Следовательно, для определения качества кластеризации требуется эксперт предметной области, который бы мог оценить осмысленность выделения кластеров.
• число кластеров, как правило, неизвестно заранее и устанавливается в соответствии с некоторым субъективным критерием. Это справедливо только для методов дискриминации, так как в методах кластеризации выделение кластеров идёт за счёт формализованного подхода на основе мер близости.
• результат кластеризации существенно зависит от метрики, выбор которой, как правило, также субъективен и определяется экспертом. Но стоит отметить, что есть ряд рекомендаций к выбору мер близости для различных задач.

Применение

В биологии

В биологии кластеризация имеет множество приложений в самых разных областях. Например, в биоинформатике с помощью нее анализируются сложные сети взаимодействующих генов, состоящие порой из сотен или даже тысяч элементов. Кластерный анализ позволяет выделить подсети, узкие места, концентраторы и другие скрытые свойства изучаемой системы, что позволяет в конечном счете узнать вклад каждого гена в формирование изучаемого феномена.

В области экологии широко применяется для выделения пространственно однородных групп организмов, сообществ и т. п. Реже методы кластерного анализа применяются для исследования сообществ во времени. Гетерогенность структуры сообществ приводит к возникновению нетривиальных методов кластерного анализа (например, метод Чекановского).

В общем стоит отметить, что исторически сложилось так, что в качестве мер близости в биологии чаще используются меры сходства , а не меры различия (расстояния).

В социологии

При анализе результатов социологических исследований рекомендуется осуществлять анализ методами иерархического агломеративного семейства, а именно методом Уорда, при котором внутри кластеров оптимизируется минимальная дисперсия, в итоге создаются кластеры приблизительно равных размеров. Метод Уорда наиболее удачен для анализа социологических данных. В качестве меры различия лучше квадратичное евклидово расстояние, которое способствует увеличению контрастности кластеров. Главным итогом иерархического кластерного анализа является дендрограмма или «сосульчатая диаграмма». При её интерпретации исследователи сталкиваются с проблемой того же рода, что и толкование результатов факторного анализа - отсутствием однозначных критериев выделения кластеров. В качестве главных рекомендуется использовать два способа - визуальный анализ дендрограммы и сравнение результатов кластеризации, выполненной различными методами.

Визуальный анализ дендрограммы предполагает «обрезание» дерева на оптимальном уровне сходства элементов выборки. «Виноградную ветвь» (терминология Олдендерфера М. С. и Блэшфилда Р. К. ) целесообразно «обрезать» на отметке 5 шкалы Rescaled Distance Cluster Combine, таким образом будет достигнут 80 % уровень сходства. Если выделение кластеров по этой метке затруднено (на ней происходит слияние нескольких мелких кластеров в один крупный), то можно выбрать другую метку. Такая методика предлагается Олдендерфером и Блэшфилдом.

Теперь возникает вопрос устойчивости принятого кластерного решения. По сути, проверка устойчивости кластеризации сводится к проверке её достоверности. Здесь существует эмпирическое правило - устойчивая типология сохраняется при изменении методов кластеризации. Результаты иерархического кластерного анализа можно проверять итеративным кластерным анализом по методу k-средних. Если сравниваемые классификации групп респондентов имеют долю совпадений более 70 % (более 2/3 совпадений), то кластерное решение принимается.

Проверить адекватность решения, не прибегая к помощи другого вида анализа, нельзя. По крайней мере, в теоретическом плане эта проблема не решена. В классической работе Олдендерфера и Блэшфилда «Кластерный анализ» подробно рассматриваются и в итоге отвергаются дополнительные пять методов проверки устойчивости:

В информатике

• Кластеризация результатов поиска - используется для «интеллектуальной» группировки результатов при поиске файлов , веб-сайтов , других объектов , предоставляя пользователю возможность быстрой навигации, выбора заведомо более релевантного подмножества и исключения заведомо менее релевантного - что может повысить юзабилити интерфейса по сравнению с выводом в виде простого сортированного по релевантности списка .
  • Clusty - кластеризующая поисковая машина компании Vivísimo
  • Nigma - российская поисковая система с автоматической кластеризацией результатов
  • Quintura - визуальная кластеризация в виде облака ключевых слов
• Сегментация изображений (англ. image segmentation ) - Кластеризация может быть использована для разбиения цифрового изображения на отдельные области с целью обнаружения границ (англ. edge detection ) или распознавания объектов .
• Интеллектуальный анализ данных (англ. data mining) - Кластеризация в Data Mining приобретает ценность тогда, когда она выступает одним из этапов анализа данных, построения законченного аналитического решения. Аналитику часто легче выделить группы схожих объектов, изучить их особенности и построить для каждой группы отдельную модель, чем создавать одну общую модель для всех данных. Таким приемом постоянно пользуются в маркетинге, выделяя группы клиентов, покупателей, товаров и разрабатывая для каждой из них отдельную стратегию.

См. также

Примечания

Ссылки

На русском языке

• www.MachineLearning.ru - профессиональный вики-ресурс, посвященный машинному обучению и интеллектуальному анализу данных

На английском языке

• COMPACT - Comparative Package for Clustering Assessment . A free Matlab package, 2006.
• P. Berkhin, Survey of Clustering Data Mining Techniques , Accrue Software, 2002.
• Jain, Murty and Flynn: Data Clustering: A Review , ACM Comp. Surv., 1999.
• for another presentation of hierarchical, k-means and fuzzy c-means see this introduction to clustering . Also has an explanation on mixture of Gaussians.
• David Dowe, Mixture Modelling page - other clustering and mixture model links.
• a tutorial on clustering
• The on-line textbook: Information Theory, Inference, and Learning Algorithms , by David J.C. MacKay includes chapters on k-means clustering, soft k-means clustering, and derivations including the E-M algorithm and the variational view of the E-M algorithm.
• «The Self-Organized Gene» , tutorial explaining clustering through competitive learning and self-organizing maps.
• kernlab - R package for kernel based machine learning (includes spectral clustering implementation)
• Tutorial - Tutorial with introduction of Clustering Algorithms (k-means, fuzzy-c-means, hierarchical, mixture of gaussians) + some interactive demos (java applets)
• Data Mining Software - Data mining software frequently utilizes clustering techniques.
• Java Competitve Learning Application A suite of Unsupervised Neural Networks for clustering. Written in Java. Complete with all source code.
• Machine Learning Software - Also contains much clustering software.

10.1.1 Основные понятия.

Пусть исследуется совокупность объектов, каждый из которых характеризуется измеренными признаками. Требуется разбить эту совокупность на однородные в некотором смысле группы. При этом практически отсутствует априорная информация о характере распределения -мерного вектора
внутри классов. Полученные в результате разбиения группы обычно называются кластерами (таксонами, образами) , методы их нахождения - кластер-анализом (численной таксономией или распознаванием образов с самообучением).

Решение задачи заключается в определении естественного расслоения результатов наблюдений на четко выраженные кластеры, лежащие друг от друга на некотором расстоянии. (Может оказаться, что множество наблюдений не обнаруживает естественного расслоения на кластеры, т.е. образует один кластер).

Обычной формой представления исходных данных в задачах кластерного анализа служит матрица

,

каждая строка которой представляет результаты измерений рассматриваемых признаков у одного из объектов.

Кластеризация предназначена для разбиения совокупности объектов на однородные группы (кластеры или классы). Если данные выборки представить как точки в признаковом пространстве, то задача кластеризации сводится к определению "сгущений точек".

Переводится понятие кластер (cluster) как "скопление", "гроздь". Синонимами термина " кластеризация " являются "автоматическая классификация ", "обучение без учителя" и "таксономия".

Цель кластеризации - поиск существующих структур. Кластеризация является описательной процедурой, она не делает никаких статистических выводов, но дает возможность провести разведочный анализ и изучить "структуру данных". Классы заранее не определены, осуществляется поиск наиболее похожих, однородных групп. Кластер можно охарактеризовать как группу объектов, имеющих общие свойства.

Характеристиками кластера можно назвать два признака:

внутренняя однородность;

внешняя изолированность.

Кластеры могут быть непересекающимися, или эксклюзивными (non-overlapping, exclusive), и пересекающимися (overlapping). Схематическое изображение непересекающихся и пересекающихся кластеров дано на рис. 10.1.

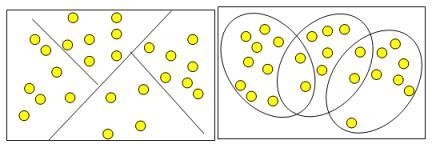
Рис. 10.1 Непересекающиеся и пересекающиеся кластеры

Термин «кластерный анализ», впервые введенный Трионом (Tryon) в 1939 году, объединяет более 100 различных алгоритмов.

В отличие от задач классификации, кластерный анализ не требует априорных предположений о наборе данных, не накладывает ограничения на представление исследуемых объектов, позволяет анализировать показатели различных типов данных (интервальные данные, частоты, бинарные данные). При этом необходимо помнить, что переменные должны измеряться в сравнимых шкалах.

10.1.2 Характеристики кластера

Кластер имеет следующие математические характеристики: центр, радиус, среднеквадратическое отклонение, размер кластера.

Каждый объект совокупности в кластерном анализе рассматривается как точка в заданном признаковом пространстве. Значение каждого из признаков у данной единицы служит ее координатой в этом пространстве.

Центр кластера - это среднее геометрическое место точек в пространстве переменных.

Радиус кластера - максимальное расстояние расположения точек от центра кластера.

Если невозможно при помощи математических процедур однозначно отнести объект к одному из двух кластеров, то такие объекты называют спорными, и обнаруживается перекрытие кластеров. Спорный объект - это объект, который по мере сходства может быть отнесен к нескольким кластерам.

Размер кластера может быть определен либо по радиусу кластера, либо по среднеквадратичному отклонению объектов для этого кластера. Объект относится к кластеру, если расстояние от объекта до центра кластера меньше радиуса кластера. Если это условие выполняется для двух и более кластеров, объект является спорным. Неоднозначность данной задачи может быть устранена экспертом или аналитиком.

Задачи кластеризации в Data Mining

Введение в кластерный анализ

Из всей обширной области применения кластерного анализа,например, задачи социально-экономического прогнозирования.

При анализе и прогнозировании социально-экономических явлений исследователь довольно часто сталкивается с многомерностью их описания. Этопроисходит при решении задачи сегментирования рынка, построении типологии стран по достаточно большому числу показателей, прогнозирования конъюнктуры рынка отдельных товаров, изучении и прогнозировании экономической депрессии и многих других проблем.

Методы многомерного анализа - наиболее действенный количественный инструмент исследования социально-экономических процессов, описываемых большимчислом характеристик. К ним относятся кластерный анализ, таксономия, распознавание образов, факторный анализ.

Кластерный анализ наиболее ярко отражает черты многомерного анализа в классификации, факторный анализ – в исследовании связи.

Иногда подход кластерного анализа называют в литературе численной таксономией, численной классификацией, распознаванием с самообучением и т.д.

Первое применение кластерный анализ нашел в социологии. Название кластерный анализ происходит от английского слова cluster – гроздь, скопление. Впервые в 1939 был определен предмет кластерного анализа и сделано его описание исследователем Трионом. Главное назначение кластерного анализа – разбиение множества исследуемых объектов и признаков на однородные в соответствующем понимании группы или кластеры. Это означает, что решается задача классификации данных и выявления соответствующей структуры в ней. Методы кластерного анализа можно применять в самых различных случаях, даже в тех случаях, когда речь идет о простой группировке, в которой все сводится к образованию групп по количественному сходству.

Большое достоинство кластерного анализа в том, что он позволяет производить разбиение объектов не по одному параметру, а по целому набору признаков. Кроме того, кластерный анализ в отличие от большинства математико-статистических методов не накладывает никаких ограничений на вид рассматриваемых объектов, и позволяет рассматривать множество исходных данных практически произвольной природы. Это имеет большое значение, например, для прогнозирования конъюнктуры, когда показатели имеют разнообразный вид, затрудняющий применение традиционных эконометрических подходов.

Кластерный анализ позволяет рассматривать достаточно большой объем информации и резко сокращать, сжимать большие массивы социально-экономической информации, делать ихкомпактными и наглядными.

Важное значение кластерный анализ имеет применительно к совокупностям временных рядов, характеризующих экономическое развитие (например, общехозяйственной и товарной конъюнктуры). Здесь можно выделять периоды, когда значения соответствующих показателей были достаточно близкими, а также определять группы временных рядов, динамика которых наиболее схожа.

Кластерный анализ можно использовать циклически. В этом случае исследование производится до тех пор, пока не будут достигнуты необходимые результаты. При этом каждый цикл здесь может давать информацию, которая способна сильно изменить направленность и подходы дальнейшего применения кластерного анализа. Этот процесс можно представить системой с обратной связью.

В задачахсоциально-экономического прогнозирования весьма перспективно сочетание кластерного анализас другими количественными методами (например, с регрессионным анализом).

Как и любой другой метод, кластерный анализ имеет определенные недостаткии ограничения : В частности, состави количество кластеров зависит отвыбираемых критериев разбиения. При сведении исходного массива данных к более компактному виду могут возникать определенные искажения, а также могут теряться индивидуальные черты отдельных объектов за счетзамены их характеристиками обобщенных значений параметров кластера. При проведении классификации объектов игнорируется очень часто возможность отсутствия в рассматриваемойсовокупности каких-либо значений кластеров.

В кластерном анализе считается, что:

а) выбранные характеристики допускают в принципе желательное разбиение на кластеры;

б) единицы измерения (масштаб) выбраны правильно.

Выбор масштаба играет большую роль. Как правило, данные нормализуют вычитанием среднего и делением на стандартное отклоненение, так что дисперсия оказывается равной единице.

1.Задача кластеризации

Задача кластеризации заключается в том, чтобы на основании данных, содержащихся во множестве Х , разбить множество объектов G на m (m – целое) кластеров (подмножеств) Q 1 , Q 2 , …, Q m , так, чтобы каждый объект G j принадлежал одному и только одному подмножеству разбиения и чтобы объекты, принадлежащие одному и тому же кластеру, были сходными, в то время, как объекты, принадлежащие разным кластерам были разнородными.

Например, пусть G включает n стран, любая из которых характеризуется ВНП на душу населения (F 1 ), числом М автомашин на 1 тысячу человек (F 2 ), душевым потреблением электроэнергии (F 3 ), душевым потреблением стали (F 4 ) и т.д. Тогда Х 1 (вектор измерений) представляет собой набор указанных характеристик для первой страны, Х 2 - для второй, Х 3 для третьей, и т.д. Задача заключается в том, чтобы разбить страны по уровню развития.

Решением задачи кластерного анализа являются разбиения, удовлетворяющие некоторому критерию оптимальности. Этот критерий может представлять собой некоторый функционал, выражающий уровни желательности различных разбиений и группировок, который называют целевой функцией. Например, в качестве целевой функции может быть взята внутригрупповая сумма квадратов отклонения:

где x j - представляет собой измерения j -го объекта.

Для решениязадачи кластерного анализа необходимо определить понятие сходства и разнородности.

Понятно то, что объекты i -ый и j -ый попадали бы в один кластер, когда расстояние (отдаленность) между точками Х i и Х j было бы достаточно маленьким и попадали бы в разные кластеры, когда это расстояние было бы достаточно большим. Таким образом, попадание в один или разные кластеры объектов определяется понятием расстояния между Х i и Х j из Ер , где Ер - р -мерное евклидово пространство. Неотрицательная функция d(Х i , Х j) называется функцией расстояния (метрикой), если:

а) d(Х i , Х j) ³ 0 , для всех Х i и Х j из Ер

б) d(Х i , Х j) = 0 , тогда и только тогда, когда Х i = Х j

в) d(Х i , Х j) = d(Х j , Х i )

г) d(Х i , Х j) £ d(Х i , Х k) + d(Х k , Х j), где Х j ; Х i и Х k - любые три вектора из Ер .

Значение d(Х i , Х j) для Х i и Х j называется расстоянием между Х i и Х j и эквивалентно расстоянию между G i и G j соответственно выбранным характеристикам (F 1 , F 2 , F 3 , ..., F р).

Наиболее часто употребляются следующие функции расстояний:

1. Евклидово расстояние d 2 (Х i , Х j) =

2. l 1 - нормаd 1 (Х i , Х j) =

3. Супремум - норма d ¥ (Х i , Х j) = sup

k = 1, 2, ..., р

4. l p - норма d р (Х i , Х j) =

Евклидова метрика является наиболее популярной. Метрика l 1 наиболее легкая для вычислений. Супремум-норма легко считается и включает в себя процедуру упорядочения, а l p - норма охватывает функции расстояний 1, 2, 3,.

Пусть n измерений Х 1 , Х 2 ,..., Х n представлены в виде матрицы данных размером p ´ n :

Тогда расстояние между парами векторов d(Х i , Х j) могут быть представлены в виде симметричной матрицы расстояний:

Понятием, противоположным расстоянию, является понятие сходства между объектами G i . и G j . Неотрицательная вещественная функция S(Х i ; Х j) = S i j называется мерой сходства, если:

1) 0 £ S(Х i , Х j) < 1 для Х i ¹ Х j

2) S( Х i , Х i ) = 1

3) S( Х i , Х j ) = S(Х j , Х i )

Пары значений мер сходства можно объединить в матрицу сходства:

Величину S ij называют коэффициентом сходства.

2. Методы кластеризации

Сегодня существует достаточно много методов кластерного анализа. Остановимся на некоторых из них (ниже приводимые методы принято называть методами минимальной дисперсии).

Пусть Х - матрица наблюдений: Х = (Х 1 , Х 2 ,..., Х u) и квадрат евклидова расстояния между Х i и Х j определяется по формуле:

1) Метод полных связей.

Суть данного метода в том, что два объекта, принадлежащих одной и той же группе (кластеру), имеют коэффициент сходства, который меньше некоторого порогового значения S . В терминах евклидова расстояния d это означает, что расстояние между двумя точками (объектами) кластера не должно превышать некоторого порогового значения h . Таким образом, h определяет максимально допустимый диаметр подмножества, образующего кластер.

2) Метод максимального локального расстояния.

Каждый объект рассматривается как одноточечный кластер. Объекты группируются по следующему правилу: два кластера объединяются, если максимальное расстояние между точками одного кластера и точками другого минимально. Процедура состоит из n - 1 шагов и результатом являются разбиения, которые совпадают со всевозможными разбиениями в предыдущем методе для любых пороговых значений.

3) Метод Ворда .

В этом методе в качестве целевой функции применяют внутригрупповую сумму квадратов отклонений, которая есть ни что иное, как сумма квадратов расстояний между каждой точкой (объектом) и средней по кластеру, содержащему этот объект. На каждом шаге объединяются такие два кластера, которые приводят к минимальному увеличению целевой функции, т.е. внутригрупповой суммы квадратов. Этот метод направлен на объединение близко расположенных кластеров.

4) Центроидный метод.

Расстояние между двумя кластерами определяется как евклидово расстояние между центрами (средними) этих кластеров:

d 2 ij =(` X – ` Y) Т (` X – ` Y) Кластеризация идет поэтапно на каждом из n–1 шагов объединяют два кластера G и p , имеющие минимальное значение d 2 ij Если n 1 много больше n 2 , то центры объединения двух кластеров близки друг к другу и характеристикивторого кластера при объединении кластеров практически игнорируются. Иногда этот метод иногда называют еще методом взвешенных групп.

3. Алгоритм последовательной кластеризации

Рассмотрим Ι = (Ι 1 , Ι 2 , … Ι n ) как множество кластеров {Ι 1 } , {Ι 2 },…{Ι n } . Выберем два из них, например, Ι i и Ι j , которые в некотором смысле более близки друг к другу и объединим их в один кластер. Новое множество кластеров, состоящее уже из n -1 кластеров, будет:

{Ι 1 }, {Ι 2 }…, {Ι i , Ι j }, …, {Ι n } .

Повторяя процесс, получим последовательные множества кластеров, состоящие из (n -2), (n -3), (n –4) и т.д. кластеров. В конце процедуры можно получить кластер, состоящий из n объектов и совпадающий с первоначальным множеством Ι = (Ι 1 , Ι 2 , … Ι n ) .

В качестве меры расстояния возьмем квадрат евклидовой метрикиd i j 2 . и вычислим матрицу D = {d i j 2 }, где d i j 2 - квадрат расстояния между

Ι i и Ι j:

				….	Ι n
		d 12 2	d 13 2	….	d 1n 2
			d 23 2	….	d 2n 2
				….	d 3n 2
….				….	….
Ι n

Пусть расстояние между Ι i и Ι j будет минимальным:

d i j 2 = min {d i j 2 , i ¹ j}. Образуем с помощью Ι i и Ι j новый кластер

{Ι i , Ι j } . Построим новую ((n-1), (n-1)) матрицу расстояния

	{ Ι i , Ι j }				….	Ι n
{ Ι i ; Ι j }		d i j 2 1	d i j 2 2		….	d i j 2 n
			d 12 2	d 1 3	….	d 1 2 n
					….	d 2 n
					….	d 3n

(n -2) строки для последней матрицы взяты из предыдущей, а первая строка вычислена заново. Вычисления могут быть сведенык минимуму, если удастся выразить d i j 2 k ,k = 1, 2,…, n ; (k ¹ i ¹ j) через элементы первоначальной матрицы.

Исходно определено расстояние лишь между одноэлементными кластерами, но надо определять расстояния и между кластерами, содержащими более чем один элемент. Это можно сделать различными способами, и в зависимости от выбранного способа мы получают алгоритмы кластер анализа с различными свойствами. Можно, например, положить расстояние между кластером i + j и некоторым другим кластером k , равным среднему арифметическому из расстояний между кластерами i и k и кластерами j и k :

d i+j,k = ½ (d i k + d j k).

Но можно также определить d i+j,k как минимальное из этих двух расстояний:

d i+j,k = min (d i k + d j k).

Таким образом, описан первый шаг работы агломеративного иерархического алгоритма. Последующие шаги аналогичны.

Довольно широкий класс алгоритмов может быть получен, если для перерасчета расстояний использовать следующую общую формулу:

d i+j,k = A(w) min(d ik d jk) + B(w) max(d ik d jk), где

A(w) = , если d ik £ d jk

A(w) = , если d ik > d jk

B(w) = , если d i k £ d jk

B (w ) = , если d ik > d jk

где n i и n j - число элементов в кластерах i и j , а w – свободный параметр, выбор которого определяет конкретный алгоритм. Например, при w = 1 мы получаем, так называемый, алгоритм «средней связи», для которого формула перерасчета расстояний принимает вид:

d i+j,k =

В данном случае расстояние между двумя кластерами на каждом шаге работы алгоритма оказывается равным среднему арифметическому из расстояний между всеми такими парами элементов, что один элемент пары принадлежитк одному кластеру, другой - к другому.

Наглядный смысл параметра w становится понятным, если положить w ® ¥ . Формула пересчета расстояний принимает вид:

d i+j,k = min (d i ,k d jk)

Это будеттак называемый алгоритм «ближайшего соседа», позволяющий выделять кластеры сколь угодно сложной формы при условии, что различные части таких кластеров соединены цепочками близких друг к другу элементов. В данном случае расстояние между двумя кластерами на каждом шаге работы алгоритма оказывается равным расстоянию между двумя самыми близкими элементами, принадлежащими к этим двум кластерам.

Довольно часто предполагают, что первоначальные расстояния (различия) между группируемыми элементамизаданы. В некоторыхзадачах это действительно так. Однако, задаются только объекты и их характеристики и матрицу расстояний строят исходя из этих данных. В зависимости от того, вычисляются ли расстояния между объектами или между характеристиками объектов, используются разные способы.

В случае кластер анализа объектов наиболее часто мерой различия служит либо квадрат евклидова расстояния

(где x ih , x jh - значения h -го признака для i -го и j -го объектов, а m - число характеристик), либо само евклидово расстояние. Если признакам приписывается разный вес, то эти веса можно учесть при вычислении расстояния

Иногда в качестве меры различияиспользуется расстояние, вычисляемое по формуле:

которые называют: "хэмминговым", "манхэттенским" или "сити-блок" расстоянием.

Естественноймерой сходства характеристик объектов во многих задачах является коэффициент корреляции между ними

где m i ,m j , d i , d j - соответственно средние и среднеквадратичные отклонения для характеристик i и j . Мерой различия между характеристиками может служить величина1 - r . В некоторых задачахзнак коэффициента корреляции несуществен и зависит лишь отвыбора единицы измерения. В этом случае в качестве меры различиямежду характеристиками используется ô 1 - r i j ô

4. Число кластеров

Очень важным вопросом является проблема выбора необходимого числа кластеров. Иногда можно m число кластеров выбирать априорно. Однако в общем случае это число определяется в процессе разбиениямножества на кластеры.

Проводились исследования Фортьером и Соломоном, и было установлено, что число кластеров должно быть принято для достижения вероятности a того, что найдено наилучшее разбиение. Таким образом, оптимальное число разбиений является функцией заданной доли b наилучших или в некотором смысле допустимых разбиений во множествевсех возможных. Общее рассеяние будет тем больше, чем выше доля b допустимых разбиений. Фортьер и Соломон разработали таблицу, по которой можно найти число необходимых разбиений. S(a , b ) в зависимости от a и b (где a - вероятность того, что найдено наилучшее разбиение, b - доля наилучших разбиений в общем числе разбиений) Причем в качестве меры разнородности используется не мера рассеяния, а мера принадлежности, введенная Хользенгером и Харманом. Таблица значений S( a , b ) приводится ниже.

Таблица значений S( a , b )

b \ a	0.20	0.10	0.05	0.01	0.001	0.0001
0.20	8	11	14	21	31	42
0.10	16	22	29	44	66	88
0.05	32	45	59	90	135	180
0.01	161	230	299	459	689	918
0.001	1626	2326	3026	4652	6977	9303
0.0001	17475	25000	32526	55000	75000	100000

Довольно часто критерием объединения (числа кластеров) становится изменение соответствующей функции. Например, суммы квадратов отклонений:

Процессу группировки должно соответствовать здесь последовательное минимальное возрастание значения критерия E . Наличие резкого скачка в значении E можно интерпретировать как характеристику числа кластеров, объективно существующих в исследуемой совокупности.

Итак, второй способ определения наилучшего числа кластеров сводится к выявлению скачков, определяемых фазовым переходом от сильно связанного к слабосвязанному состоянию объектов.

5. Дендограммы

Наиболее известный метод представления матрицы расстояний или сходства основан на идее дендограммы или диаграммы дерева. Дендограмму можно определить как графическое изображение результатов процессапоследовательной кластеризации, которая осуществляется в терминах матрицы расстояний. С помощью дендограммы можно графически или геометрически изобразить процедуру кластеризации при условии, что эта процедура оперирует толькос элементами матрицы расстояний или сходства.

Существуетмного способов построения дендограмм. В дендограмме объектырасполагаются вертикально слева, результатыкластеризации – справа. Значения расстояний или сходства, отвечающие строению новых кластеров, изображаются по горизонтальной прямой поверх дендограмм.

Рис1

На рисунке 1 показан один из примеровдендограммы. Рис 1 соответствует случаю шести объектов ( n =6) и k характеристик (признаков). Объекты А и С наиболее близки и поэтому объединяются в один кластер на уровне близости, равном 0,9. Объекты D и Е объединяютсяпри уровне 0,8. Теперь имеем 4 кластера:

(А, С), ( F ), ( D , E ), ( B ) .

Далее образуются кластеры (А, С, F ) и ( E , D , B ) , соответствующие уровню близости, равному 0,7 и 0,6. Окончательно все объекты группируются в один кластер при уровне 0,5.

Вид дендограммы зависит от выбора меры сходстваили расстояния между объектоми кластером и метода кластеризации. Наиболее важным моментом является выбор меры сходства или меры расстояния между объектом и кластером.

Число алгоритмов кластерного анализа слишком велико. Все их можноподразделить на иерархическиеи неиерархические.

Иерархические алгоритмы связаны с построением дендограмм и делятся на:

а) агломеративные, характеризуемые последовательным объединениемисходных элементов и соответствующим уменьшением числа кластеров;

б) дивизимные (делимые), в которых число кластеров возрастает, начиная с одного, в результате чего образуется последовательностьрасщепляющих групп.

Алгоритмы кластерного анализа имеют сегодня хорошую программную реализацию, которая позволяет решить задачи самой большой размерности.

6. Данные

Кластерный анализ можно применять к интервальным данным, частотам, бинарным данным. Важно, чтобы переменные изменялись в сравнимых шкалах.

Неоднородность единиц измерения и вытекающая отсюда невозможность обоснованного выражения значений различных показателей в одном масштабе приводит к тому, что величина расстояний между точками, отражающими положение объектов в пространстве их свойств, оказывается зависящей от произвольно избираемого масштаба. Чтобы устранить неоднородность измерения исходных данных, все их значения предварительно нормируются, т.е. выражаются через отношение этих значенийк некоторой величине, отражающей определенные свойства данного показателя. Нормирование исходных данных для кластерного анализа иногда проводится посредством деления исходных величин на среднеквадратичное отклонение соответствующих показателей. Другой способ сводиться к вычислению, так называемого, стандартизованного вклада. Его еще называют Z -вкладом.

Z -вклад показывает, сколько стандартных отклонений отделяет данное наблюдение от среднего значения:

Где x i – значение данного наблюдения, – среднее, S – стандартное отклонение.

Среднее для Z -вкладов является нулевым и стандартное отклонение равно 1.

Стандартизация позволяет сравнивать наблюдения из различных распределений. Если распределение переменной является нормальным (или близким к нормальному), и средняя и дисперсия известны или оцениваются по большим выборным, то Z -вклад для наблюдения обеспечивает более специфическую информацию о его расположении.

Заметим, что методы нормирования означают признание всех признаков равноценными с точки зрения выяснения сходства рассматриваемых объектов. Уже отмечалось, что применительно к экономике признание равноценности различных показателей кажется оправданным отнюдь не всегда. Было бы, желательным наряду с нормированием придать каждому из показателей вес, отражающий его значимость в ходе установления сходств и различий объектов.

В этой ситуации приходится прибегать к способу определения весов отдельных показателей – опросу экспертов. Например, при решении задачи о классификации стран по уровню экономического развития использовались результаты опроса 40 ведущих московских специалистов по проблемам развитых стран по десятибалльной шкале:

обобщенные показатели социально-экономического развития – 9 баллов;

показатели отраслевого распределения занятого населения – 7 баллов;

показатели распространенности наемного труда – 6 баллов;

показатели, характеризующие человеческий элемент производительных сил – 6 баллов;

показатели развития материальных производительных сил – 8 баллов;

показатель государственных расходов – 4балла;

«военно-экономические» показатели – 3 балла;

социально-демографические показатели – 4 балла.

Оценки экспертов отличались сравнительно высокой устойчивостью.

Экспертные оценки дают известное основание для определения важности индикаторов, входящих в ту или иную группу показателей. Умножение нормированных значений показателей на коэффициент, соответствующий среднему баллу оценки, позволяет рассчитывать расстояния между точками, отражающими положение стран в многомерном пространстве, с учетом неодинакового веса их признаков.

Довольно часто при решенииподобных задач используют не один, а два расчета: первый, в котором все признаки считаются равнозначными, второй, где им придаются различные веса в соответствии со средними значениями экспертных оценок.

7. Применение кластерного анализа

Рассмотрим некоторые приложения кластерного анализа.

1. Деление стран на группы по уровню развития.

Изучались 65 стран по 31 показателю (национальный доход на душу населения, доля населения занятого в промышленности в %, накопления на душу населения, доля населения, занятого в сельском хозяйстве в %, средняя продолжительность жизни, число автомашин на 1 тыс. жителей, численность вооруженных сил на 1 млн. жителей, доля ВВП промышленности в %, доля ВВП сельского хозяйства в %, и т.д.)

Каждая из стран выступает в данном рассмотрении как объект, характеризуемый определенными значениями 31 показателя. Соответственно они могут быть представлены в качестве точек в 31-мерном пространстве. Такое пространство обычно называется пространством свойств изучаемых объектов. Сравнениерасстояния между этими точками будет отражать степень близости рассматриваемых стран, их сходство друг с другом. Социально-экономический смысл подобного понимания сходства означает, что страны считаются тем более похожими, чем меньше различия между одноименными показателями, с помощью которых они описываются.

Первый шаг подобного анализа заключается в выявлении пары народных хозяйств, учтенных в матрице сходства, расстояние между которыми является наименьшим. Это, очевидно, будут наиболее сходные, похожие экономики. В последующем рассмотрении обе эти страны считаются единой группой, единым кластером. Соответственно исходная матрица преобразуется так, что ее элементами становятся расстояния между всеми возможными парами уже не 65, а 64 объектами – 63 экономики и вновь преобразованного кластера – условного объединения двух наиболее похожих стран. Из исходной матрицы сходства выбрасываются строки и столбцы, соответствующие расстояниям от пары стран, вошедших в объедение, до всех остальных, но зато добавляются строка и столбец, содержащие расстояние между кластером, полученным при объединении и прочими странами.

Расстояние между вновь полученным кластером и странами полагается равным среднему из расстояний между последними и двумя странами, которые составляют новый кластер. Иными словами, объединенная группа стран рассматривается как целоес характеристиками, примерно равными средним из характеристик входящих в него стран.

Второй шаг анализа заключается в рассмотрении преобразованной таким путем матрицы с 64 строками и столбцами. Снова выявляется пара экономик, расстояние между которыми имеет наименьшее значение, и они, так же как в первом случае, сводятся воедино. При этом наименьшее расстояниеможет оказаться как между парой стран, таки между какой-либо странойи объединением стран, полученным на предыдущем этапе.

Дальнейшие процедуры аналогичны описанным выше: на каждом этапе матрица преобразуется так, что из нее исключаются два столбца и две строки, содержащие расстояние до объектов (пар стран или объединений – кластеров), сведенных воедино на предыдущей стадии; исключенные строки и столбцы заменяются столбцоми строкой, содержащими расстояния от новых объединений до остальных объектов; далее в измененной матрице выявляется пара наиболее близких объектов. Анализ продолжается до полного исчерпания матрицы (т. е. до тех пор, пока все страны не окажутся сведенными в одно целое). Обобщенные результаты анализа матрицы можно представить в виде дерева сходства (дендограммы), подобного описанному выше, с той лишь разницей, что дерево сходства, отражающее относительную близость всех рассматриваемых нами 65 стран, много сложнее схемы, в которой фигурирует только пять народных хозяйств. Это дерево в соответствиис числом сопоставляемых объектов включает 65 уровней. Первый (нижний) уровень содержит точки, соответствующие каждых стране в отдельности. Соединение двух этих точек на втором уровне показывает пару стран, наиболее близких по общему типу народных хозяйств. На третьем уровне отмечается следующее по сходству парное соотношение стран (как уже упоминалось, в таком соотношении может находиться либо новая пара стран, либо новая странаи уже выявленная пара сходных стран). И так далее до последнего уровня, на котором все изучаемые страны выступают как единая совокупность.

В результате применения кластерного анализа были получены следующие пять групп стран:

· афро-азиатская группа;

· латино-азиатская группа;

· латино-среднеземнаморская группа;

· группа развитых капиталистических стран (без США)

· США

Введение новых индикаторов сверх используемого здесь 31 показателя или замена их другими, естественно, приводят к изменению результатов классификации стран.

2. Деление стран по критерию близости культуры.

Как известно маркетинг должен учитывать культуру стран (обычаи, традиции, и т.д.).

Посредством кластеризации были получены следующие группы стран:

· арабские;

· ближневосточные;

· скандинавские;

· германоязычные;

· англоязычные;

· романские европейские;

· латиноамериканские;

· дальневосточные.

3. Разработка прогноза конъюнктуры рынка цинка.

Кластерный анализ играет важную рольна этапе редукции экономико-математической модели товарной конъюнктуры, способствуя облегчению и упрощению вычислительных процедур, обеспечению большей компактности получаемых результатов при одновременном сохранении необходимой точности. Применение кластерного анализа дает возможность разбить всю исходную совокупность показателей конъюнктуры на группы (кластеры) по соответствующим критериям, облегчая тем самым выбор наиболее репрезентативных показателей.

Кластерный анализ широко используется для моделирования рыночной конъюнктуры. Практически основное большинство задач прогнозирования опирается наиспользование кластерного анализа.

Например, задача разработки прогноза конъюнктуры рынка цинка.

Первоначально было отобрано 30 основных показателей мирового рынка цинка:

Х 1 - время

Показатели производства:

Х 2 - в мире

Х 4 - Европе

Х 5 - Канаде

Х 6 - Японии

Х 7 - Австралии

Показатели потребления:

Х 8 - в мире

Х 10 - Европе

Х 11 - Канаде

Х 12 - Японии

Х 13 - Австралии

Запасы цинка у производителей:

Х 14 - в мире

Х 16 - Европе

Х 17 - других странах

Запасы цинка у потребителей:

Х 18 - в США

Х 19 - в Англии

Х 10 - в Японии

Импорт цинковых руд и концентратов (тыс. тонн)

Х 21 - в США

Х 22 - в Японии

Х 23 - в ФРГ

Экспорт цинковых руд и концентратов (тыс. тонн)

Х 24 - из Канады

Х 25 - из Австралии

Импорт цинка (тыс. тонн)

Х 26 - в США

Х 27 - в Англию

Х 28 - в ФРГ

Экспорт цинка (тыс. Тонн)

Х 29 -из Канады

Х 30 - из Австралии

Для определения конкретныхзависимостей был использован аппарат корреляционно-регрессионногоанализа. Анализ связей производился на основе матрицы парных коэффициентов корреляции. Здесь принималась гипотеза о нормальном распределении анализируемых показателей конъюнктуры.Ясно, что r ij являются не единственно возможным показателем связи используемых показателей. Необходимость использования кластерного анализа связано в этой задачес тем, что число показателей влияющих нацену цинка очень велико. Возникает необходимость их сократить по целому ряду следующих причин:

а) отсутствие полных статистических данных по всем переменным;

б) резкое усложнение вычислительных процедур при введении в модель большого числа переменных;

в) оптимальное использование методов регрессионного анализа требует превышения числа наблюдаемых значений над числом переменных не менее, чем в 6-8 раз;

г) стремление к использованию в модели статистически независимых переменных и пр.

Проводить такой анализ непосредственно на сравнительно громоздкой матрице коэффициентов корреляции весьма затруднительно. С помощью кластерного анализа всю совокупность конъюнктурных переменных можно разбить на группы таким образом, чтобы элементы каждого кластера сильно коррелировали между собой, а представители разных групп характеризовались слабой коррелированностью.

Для решения этой задачи был применен один из агломеративных иерархических алгоритмов кластерного анализа. На каждом шаге число кластеров уменьшается на один за счет оптимального, в определенном смысле, объединения двух групп. Критерием объединения является изменение соответствующей функции. В качестве функции такой были использованы значения сумм квадратов отклонений вычисляемые по следующим формулам:

(j = 1, 2, …, m ),

где j - номер кластера, n - число элементов в кластере.

r ij -коэффициент парной корреляции.

Таким образом, процессу группировки должно соответствовать последовательное минимальное возрастание значения критерия E .

На первом этапе первоначальный массив данных представляется в виде множества, состоящего из кластеров, включающих в себя по одному элементу. Процесс группировки начинается с объединения такой пары кластеров, которое приводит к минимальному возрастанию суммы квадратов отклонений. Это требует оценки значений суммы квадратов отклонений для каждогоиз возможных объединений кластеров. На следующем этапе рассматриваются значения сумм квадратов отклонений уже для кластеров и т.д. Этот процесс будет остановлен на некотором шаге. Для этого нужно следить за величиной суммы квадратов отклонений. Рассматривая последовательность возрастающих величин, можно уловить скачок (один или несколько) в ее динамике, который можно интерпретировать как характеристику числа групп «объективно» существующих в исследуемойсовокупности. В приведенном примере скачки имели место при числе кластеров равном 7 и 5. Далее снижать число групп не следует, т.к. это приводит к снижению качества модели. После получения кластеров происходит выбор переменных наиболее важных в экономическом смысле и наиболее тесно связанных с выбранным критерием конъюнктуры - в данном случае с котировками Лондонской биржи металлов на цинк. Этот подход позволяет сохранить значительную часть информации, содержащейся в первоначальном наборе исходных показателей конъюнктуры.

Часто в самых различных областях деятельности нам приходится иметь дело с огромным количеством каких-либо предметов, в отношении которых требуется принять меры.

А мы не можем даже осознать весь этот объем, а не то что разобраться в нем.

Какой же выход? Ну, конечно, «разложить все по полочкам». В данном случае народная мудрость обретает вполне определенную научную формулировку.

Кластерный анализ – это исследование объектов путем объединения их по однородным группам со схожими признаками. Его методы применимы буквально во всех сферах: от медицины до торговли на Форекс, от автострахования до археологии. А для маркетологов и спецов по кадрам он просто незаменим.

Об этом подробнее – в статье.

Что такое кластер

Кластерный анализ предназначен для разбиения совокупности объектов на однородные группы (кластеры или классы). Это задача многомерной классификации данных.

Существует около 100 разных алгоритмов кластеризации, однако, наиболее часто используемые:

1. иерархический кластерный анализ,
2. кластеризация методом k-средних.

Где применяется кластерный анализ:

• В маркетинге это сегментация конкурентов и потребителей.
• В менеджменте:
  1. разбиение персонала на различные по уровню мотивации группы,
  2. классификация поставщиков,
  3. выявление схожих производственных ситуаций, при которых возникает брак.
• В медицине - классификация симптомов, пациентов, препаратов.
• В социологии - разбиение респондентов на однородные группы.

По сути кластерный анализ хорошо зарекомендовал себя во всех сферах жизнедеятельности человека. Прелесть данного метода - он работает даже тогда, когда данных мало и не выполняются требования нормальности распределений случайных величин и другие требования классических методов статистического анализа.

Поясним суть кластерного анализа, не прибегая к строгой терминологии.

Допустим, Вы провели анкетирование сотрудников и хотите определить, каким образом можно наиболее эффективно управлять персоналом. То есть Вы хотите разделить сотрудников на группы и для каждой из них выделить наиболее эффективные рычаги управления. При этом различия между группами должны быть очевидными, а внутри группы респонденты должны быть максимально похожи.

Для решения задачи предлагается использовать иерархический кластерный анализ. В результате мы получим дерево, глядя на которое мы должны определиться, на сколько классов (кластеров) мы хотим разбить персонал. Предположим, что мы решили разбить персонал на три группы, тогда для изучения респондентов, попавших в каждый кластер получим табличку примерно следующего содержания:

Поясним, как сформирована приведенная выше таблица. В первом столбце расположен номер кластера - группы, данные по которой отражены в строке. Например, первый кластер на 80% составляют мужчины. 90% первого кластера попадают в возрастную категорию от 30 до 50 лет, а 12% респондентов считает, что льготы очень важны. И так далее.

Попытаемся составить портреты респондентов каждого кластера:

1. Первая группа — в основном мужчины зрелого возраста, занимающие руководящие позиции. Соцпакет (MED, LGOTI, TIME-свободное время) их не интересует. Они предпочитают получать хорошую зарплату, а не помощь от работодателя.
2. Группа два — наоборот, отдает предпочтение соцпакету. Состоит она, в основном, из людей «в возрасте», занимающих невысокие посты. Зарплата для них безусловно важна, но есть и другие приоритеты.
3. Третья группа — наиболее «молодая». В отличие от предыдущих двух, очевиден интерес к возможностям обучения и профессионального роста. У этой категории сотрудников есть хороший шанс в скором времени пополнить первую группу.

Таким образом, планируя кампанию по внедрению эффективных методов управления персоналом, очевидно, что в нашей ситуации можно увеличить соцпакет у второй группы в ущерб, к примеру, зарплате. Если говорить о том, каких специалистов следует направлять на обучение, то можно однозначно рекомендовать обратить внимание на третью группу.

Источник: "nickart.spb.ru"

Кластерный анализ — это ключ к пониманию рынка

Кластер - это цена актива в определенный промежуток времени, на котором совершались сделки. Результирующий объем покупок и продаж указан цифрой внутри кластера. Бар любого ТФ вмещает в себя, как правило, несколько кластеров. Это позволяет детально видеть объемы покупок, продаж и их баланс в каждом отдельном баре, по каждому ценовому уровню.

Построение кластерного графика

Изменение цены одного актива неизбежно влечет за собой цепочку ценовых движений и на других инструментах. В большинстве случаев понимание трендового движения происходит уже в тот момент, когда оно бурно развивается, и вход в рынок по тренду чреват попаданием в коррекционную волну.

Для успешных сделок необходимо понимать текущую ситуацию и уметь предвидеть будущие ценовые движения. Этому можно научиться, анализируя график кластеров. С помощью кластерного анализа можно видеть активность участников рынка внутри даже самого маленького ценового бара.

Это наиболее точный и детальный анализ, так как показывает точечное распределение объемов сделок по каждому ценовому уровню актива. На рынке постоянно идет противоборство интересов продавцов и покупателей. И каждое самое маленькое движение цены (тик), является тем ходом к компромиссу – ценовому уровню - который в данный момент устраивает обе стороны.

Но рынок динамичен, количество продавцов и покупателей непрерывно изменяется. Если в один момент времени на рынке доминировали продавцы, то в следующий момент, вероятнее всего, будут покупатели. Не одинаковым оказывается и количество совершенных сделок на соседних ценовых уровнях.

И все же сначала рыночная ситуация отражается на суммарных объемах сделок, а уж затем на цене. Если видеть действия доминирующих участников рынка (продавцов или покупателей), то можно предсказывать и само движение цены.

Для успешного применения кластерного анализа прежде всего следует понять, что такое кластер и дельта:

• Кластером называют ценовое движение, которое разбито на уровни, на которых совершались сделки с известными объемами.
• Дельта показывает разницу между покупками и продажами, происходящими в каждом кластере.

Кластерный график

Каждый кластер, или группа дельт, позволяет разобраться в том, покупатели или продавцы преобладают на рынке в данный момент времени. Достаточно лишь подсчитать общую дельту, просуммировав продажи и покупки. Если дельта отрицательна, то рынок перепродан, на нем избыточными являются сделки на продажу. Когда же дельта положительна, то на рынке явно доминируют покупатели.

Сама дельта может принимать нормальное или критическое значение. Значение объема дельты сверх нормального в кластере выделяют красным цветом. Если дельта умеренна, то это характеризует флетовое состояние на рынке. При нормальном значении дельты на рынке наблюдается трендовое движение, а вот критическое значение всегда является предвестником разворота цены.

Торговля на Форекс с помощью КА

Для получения максимальной прибыли нужно уметь определить переход дельты из умеренного уровня в нормальный. Ведь в этом случае можно заметить само начало перехода от флета к трендовому движению и суметь получить наибольшую прибыль.

Более наглядным является кластерный график, на нем можно увидеть значимые уровни накопления и распределения объемов, построить уровни поддержки и сопротивления.

Это позволяет трейдеру найти точный вход в сделку. Используя дельту, можно судить о преобладании на рынке продаж или покупок. Кластерный анализ позволяет наблюдать сделки и отслеживать их объемы внутри бара любого ТФ. Особо это важно при подходе к значимым уровням поддержки или сопротивления. Суждения по кластерам - ключ к пониманию рынка.

Источник: "orderflowtrading.ru"

Области и особенности применения анализа кластеров

Термин кластерный анализ (впервые ввел Tryon, 1939) в действительности включает в себя набор различных алгоритмов классификации. Общий вопрос, задаваемый исследователями во многих областях, состоит в том, как организовать наблюдаемые данные в наглядные структуры, т.е. развернуть таксономии.

Например, биологи ставят цель разбить животных на различные виды, чтобы содержательно описать различия между ними. В соответствии с современной системой, принятой в биологии, человек принадлежит к приматам, млекопитающим, амниотам, позвоночным и животным.

Заметьте, что в этой классификации чем выше уровень агрегации, тем меньше сходства между членами в соответствующем классе. Человек имеет больше сходства с другими приматами (т.е. с обезьянами), чем с «отдаленными» членами семейства млекопитающих (например, собаками) и т.д.

Заметим, что предыдущие рассуждения ссылаются на алгоритмы кластеризации, но ничего не упоминают о проверке статистической значимости. Фактически, кластерный анализ является не столько обычным статистическим методом, сколько «набором» различных алгоритмов «распределения объектов по кластерам».

Существует точка зрения, что в отличие от многих других статистических процедур, методы кластерного анализа используются в большинстве случаев тогда, когда вы не имеете каких-либо априорных гипотез относительно классов, но все еще находитесь в описательной стадии исследования. Следует понимать, что кластерный анализ определяет «наиболее возможно значимое решение».

Поэтому проверка статистической значимости в действительности здесь неприменима, даже в случаях, когда известны p-уровни (как, например, в методе K средних).

Техника кластеризации применяется в самых разнообразных областях. Хартиган (Hartigan, 1975) дал прекрасный обзор многих опубликованных исследований, содержащих результаты, полученные методами кластерного анализа. Например, в области медицины кластеризация заболеваний, лечения заболеваний или симптомов заболеваний приводит к широко используемым таксономиям.

В области психиатрии правильная диагностика кластеров симптомов, таких как паранойя, шизофрения и т.д., является решающей для успешной терапии. В археологии с помощью кластерного анализа исследователи пытаются установить таксономии каменных орудий, похоронных объектов и т.д.

Известны широкие применения кластерного анализа в маркетинговых исследованиях. В общем, всякий раз, когда необходимо классифицировать «горы» информации к пригодным для дальнейшей обработки группам, кластерный анализ оказывается весьма полезным и эффективным.

Древовидная кластеризация

Назначение алгоритма объединения (древовидной кластеризации) состоит в объединении объектов (например, животных) в достаточно большие кластеры, используя некоторую меру сходства или расстояние между объектами. Типичным результатом такой кластеризации является иерархическое дерево.

Рассмотрим горизонтальную древовидную диаграмму. Диаграмма начинается с каждого объекта в классе (в левой части диаграммы). Теперь представим себе, что постепенно (очень малыми шагами) вы «ослабляете» ваш критерий о том, какие объекты являются уникальными, а какие нет. Другими словами, вы понижаете порог, относящийся к решению об объединении двух или более объектов в один кластер.

В результате, вы связываете вместе все большее и большее число объектов и агрегируете (объединяете) все больше и больше кластеров, состоящих из все сильнее различающихся элементов. Окончательно, на последнем шаге все объекты объединяются вместе.

На этих диаграммах горизонтальные оси представляют расстояние объединения (в вертикальных древовидных диаграммах вертикальные оси представляют расстояние объединения). Так, для каждого узла в графе (там, где формируется новый кластер) вы можете видеть величину расстояния, для которого соответствующие элементы связываются в новый единственный кластер.

Когда данные имеют ясную «структуру» в терминах кластеров объектов, сходных между собой, тогда эта структура, скорее всего, должна быть отражена в иерархическом дереве различными ветвями. В результате успешного анализа методом объединения появляется возможность обнаружить кластеры (ветви) и интерпретировать их.

Меры расстояния

Объединение или метод древовидной кластеризации используется при формировании кластеров несходства или расстояния между объектами. Эти расстояния могут определяться в одномерном или многомерном пространстве. Например, если вы должны кластеризовать типы еды в кафе, то можете принять во внимание количество содержащихся в ней калорий, цену, субъективную оценку вкуса и т.д.

Наиболее прямой путь вычисления расстояний между объектами в многомерном пространстве состоит в вычислении евклидовых расстояний. Если вы имеете двух- или трехмерное пространство, то эта мера является реальным геометрическим расстоянием между объектами в пространстве (как будто расстояния между объектами измерены рулеткой).

Однако алгоритм объединения не «заботится» о том, являются ли «предоставленные» для этого расстояния настоящими или некоторыми другими производными мерами расстояния, что более значимо для исследователя; и задачей исследователей является подобрать правильный метод для специфических применений.

1. Евклидово расстояние.

Это, по-видимому, наиболее общий тип расстояния. Оно попросту является геометрическим расстоянием в многомерном пространстве и вычисляется следующим образом:

Заметим, что евклидово расстояние (и его квадрат) вычисляется по исходным, а не по стандартизованным данным. Это обычный способ его вычисления, который имеет определенные преимущества (например, расстояние между двумя объектами не изменяется при введении в анализ нового объекта, который может оказаться выбросом).

Тем не менее, на расстояния могут сильно влиять различия между осями, по координатам которых вычисляются эти расстояния.

К примеру, если одна из осей измерена в сантиметрах, а вы потом переведете ее в миллиметры (умножая значения на 10), то окончательное евклидово расстояние (или квадрат евклидова расстояния), вычисляемое по координатам, сильно изменится, и, как следствие, результаты кластерного анализа могут сильно отличаться от предыдущих.

2. Квадрат евклидова расстояния.

Иногда может возникнуть желание возвести в квадрат стандартное евклидово расстояние, чтобы придать большие веса более отдаленным друг от друга объектам. Это расстояние вычисляется следующим образом:

3. Расстояние городских кварталов (манхэттенское расстояние).

Это расстояние является просто средним разностей по координатам. В большинстве случаев эта мера расстояния приводит к таким же результатам, как и для обычного расстояния Евклида.

Однако отметим, что для этой меры влияние отдельных больших разностей (выбросов) уменьшается (так как они не возводятся в квадрат). Манхэттенское расстояние вычисляется по формуле:

4. Расстояние Чебышева.

Это расстояние может оказаться полезным, когда желают определить два объекта как «различные», если они различаются по какой-либо одной координате (каким-либо одним измерением). Расстояние Чебышева вычисляется по формуле:

5. Степенное расстояние.

   Иногда желают прогрессивно увеличить или уменьшить вес, относящийся к размерности, для которой соответствующие объекты сильно отличаются. Это может быть достигнуто с использованием степенного расстояния. Степенное расстояние вычисляется по формуле:

   где r и p - параметры, определяемые пользователем.

   Несколько примеров вычислений могут показать, как «работает» эта мера:

   • Параметр p ответственен за постепенное взвешивание разностей по отдельным координатам.
   • Параметр r ответственен за прогрессивное взвешивание больших расстояний между объектами.
   • Если оба параметра - r и p, равны двум, то это расстояние совпадает с расстоянием Евклида.
6. Процент несогласия.

Эта мера используется в тех случаях, когда данные являются категориальными. Это расстояние вычисляется по формуле:

Правила объединения или связи

На первом шаге, когда каждый объект представляет собой отдельный кластер, расстояния между этими объектами определяются выбранной мерой. Однако когда связываются вместе несколько объектов, возникает вопрос, как следует определить расстояния между кластерами?

Другими словами, необходимо правило объединения или связи для двух кластеров. Здесь имеются различные возможности: например, вы можете связать два кластера вместе, когда любые два объекта в двух кластерах ближе друг к другу, чем соответствующее расстояние связи.

Другими словами, вы используете «правило ближайшего соседа» для определения расстояния между кластерами; этот метод называется методом одиночной связи. Это правило строит «волокнистые» кластеры, т.е. кластеры, «сцепленные вместе» только отдельными элементами, случайно оказавшимися ближе остальных друг к другу.

Как альтернативу вы можете использовать соседей в кластерах, которые находятся дальше всех остальных пар объектов друг от друга. Этот метод называется метод полной связи. Существует также множество других методов объединения кластеров, подобных тем, что были рассмотрены.

• Одиночная связь (метод ближайшего соседа).

Как было описано выше, в этом методе расстояние между двумя кластерами определяется расстоянием между двумя наиболее близкими объектами (ближайшими соседями) в различных кластерах.

Это правило должно, в известном смысле, нанизывать объекты вместе для формирования кластеров, и результирующие кластеры имеют тенденцию быть представленными длинными «цепочками».

• Полная связь (метод наиболее удаленных соседей).

В этом методе расстояния между кластерами определяются наибольшим расстоянием между любыми двумя объектами в различных кластерах (т.е. «наиболее удаленными соседями»).

Этот метод обычно работает очень хорошо, когда объекты происходят на самом деле из реально различных «рощ».

Если же кластеры имеют в некотором роде удлиненную форму или их естественный тип является «цепочечным», то этот метод непригоден.

• Невзвешенное попарное среднее.

В этом методе расстояние между двумя различными кластерами вычисляется как среднее расстояние между всеми парами объектов в них. Метод эффективен, когда объекты в действительности формируют различные «рощи», однако он работает одинаково хорошо и в случаях протяженных («цепочного» типа) кластеров.

Отметим, что в своей книге Снит и Сокэл (Sneath, Sokal, 1973) вводят аббревиатуру UPGMA для ссылки на этот метод, как на метод невзвешенного попарного арифметического среднего - unweighted pair-group method using arithmetic averages.

• Взвешенное попарное среднее.
Метод идентичен методу невзвешенного попарного среднего, за исключением того, что при вычислениях размер соответствующих кластеров (т.е. число объектов, содержащихся в них) используется в качестве весового коэффициента. Поэтому предлагаемый метод должен быть использован, когда предполагаются неравные размеры кластеров.


В книге Снита и Сокэла (Sneath, Sokal, 1973) вводится аббревиатура WPGMA для ссылки на этот метод, как на метод взвешенного попарного арифметического среднего - weighted pair-group method using arithmetic averages.

• Невзвешенный центроидный метод.

В этом методе расстояние между двумя кластерами определяется как расстояние между их центрами тяжести.

Снит и Сокэл (Sneath and Sokal (1973)) используют аббревиатуру UPGMC для ссылки на этот метод, как на метод невзвешенного попарного центроидного усреднения - unweighted pair-group method using the centroid average.

• Взвешенный центроидный метод (медиана).

Этот метод идентичен предыдущему, за исключением того, что при вычислениях используются веса для учета разницы между размерами кластеров (т.е. числами объектов в них).

Поэтому, если имеются (или подозреваются) значительные отличия в размерах кластеров, этот метод оказывается предпочтительнее предыдущего.

Снит и Сокэл (Sneath, Sokal 1973) использовали аббревиатуру WPGMC для ссылок на него, как на метод невзвешенного попарного центроидного усреднения - weighted pair-group method using the centroid average.

• Метод Варда.

Этот метод отличается от всех других методов, поскольку он использует методы дисперсионного анализа для оценки расстояний между кластерами. Метод минимизирует сумму квадратов (SS) для любых двух (гипотетических) кластеров, которые могут быть сформированы на каждом шаге.

Подробности можно найти в работе Варда (Ward, 1963). В целом метод представляется очень эффективным, однако он стремится создавать кластеры малого размера.

Двувходовое объединение

Ранее этот метод обсуждался в терминах «объектов», которые должны быть кластеризованы. Во всех других видах анализа интересующий исследователя вопрос обычно выражается в терминах наблюдений или переменных. Оказывается, что кластеризация, как по наблюдениям, так и по переменным может привести к достаточно интересным результатам.

Например, представьте, что медицинский исследователь собирает данные о различных характеристиках (переменные) состояний пациентов (наблюдений), страдающих сердечными заболеваниями. Исследователь может захотеть кластеризовать наблюдения (пациентов) для определения кластеров пациентов со сходными симптомами.

В то же самое время исследователь может захотеть кластеризовать переменные для определения кластеров переменных, которые связаны со сходным физическим состоянием. После этого обсуждения, относящегося к тому, кластеризовать наблюдения или переменные, можно задать вопрос, а почему бы не проводить кластеризацию в обоих направлениях?

Модуль Кластерный анализ содержит эффективную двувходовую процедуру объединения, позволяющую сделать именно это. Однако двувходовое объединение используется (относительно редко) в обстоятельствах, когда ожидается, что и наблюдения и переменные одновременно вносят вклад в обнаружение осмысленных кластеров.

Так, возвращаясь к предыдущему примеру, можно предположить, что медицинскому исследователю требуется выделить кластеры пациентов, сходных по отношению к определенным кластерам характеристик физического состояния.

Трудность с интерпретацией полученных результатов возникает вследствие того, что сходства между различными кластерами могут происходить из (или быть причиной) некоторого различия подмножеств переменных. Поэтому получающиеся кластеры являются по своей природе неоднородными.

Возможно это кажется вначале немного туманным; в самом деле, в сравнении с другими описанными методами кластерного анализа, двувходовое объединение является, вероятно, наименее часто используемым методом. Однако некоторые исследователи полагают, что он предлагает мощное средство разведочного анализа данных (за более подробной информацией вы можете обратиться к описанию этого метода у Хартигана (Hartigan, 1975)).

Метод K средних

Этот метод кластеризации существенно отличается от таких агломеративных методов, как Объединение (древовидная кластеризация) и Двувходовое объединение. Предположим, вы уже имеете гипотезы относительно числа кластеров (по наблюдениям или по переменным).

Вы можете указать системе образовать ровно три кластера так, чтобы они были настолько различны, насколько это возможно. Это именно тот тип задач, которые решает алгоритм метода K средних. В общем случае метод K средних строит ровно K различных кластеров, расположенных на возможно больших расстояниях друг от друга.

В примере с физическим состоянием, медицинский исследователь может иметь «подозрение» из своего клинического опыта, что его пациенты в основном попадают в три различные категории. Далее он может захотеть узнать, может ли его интуиция быть подтверждена численно, то есть, в самом ли деле кластерный анализ K средних даст три кластера пациентов, как ожидалось?

Если это так, то средние различных мер физических параметров для каждого кластера будут давать количественный способ представления гипотез исследователя (например, пациенты в кластере 1 имеют высокий параметр 1, меньший параметр 2 и т.д.).

С вычислительной точки зрения вы можете рассматривать этот метод, как дисперсионный анализ «наоборот».

Программа начинает с K случайно выбранных кластеров, а затем изменяет принадлежность объектов к ним, чтобы:

1. минимизировать изменчивость внутри кластеров,
2. максимизировать изменчивость между кластерами.

Данный способ аналогичен методу «дисперсионный анализ (ANOVA) наоборот» в том смысле, что критерий значимости в дисперсионном анализе сравнивает межгрупповую изменчивость с внутригрупповой при проверке гипотезы о том, что средние в группах отличаются друг от друга.

В кластеризации методом K средних программа перемещает объекты (т.е. наблюдения) из одних групп (кластеров) в другие для того, чтобы получить наиболее значимый результат при проведении дисперсионного анализа (ANOVA). Обычно, когда результаты кластерного анализа методом K средних получены, можно рассчитать средние для каждого кластера по каждому измерению, чтобы оценить, насколько кластеры различаются друг от друга.

В идеале вы должны получить сильно различающиеся средние для большинства, если не для всех измерений, используемых в анализе. Значения F-статистики, полученные для каждого измерения, являются другим индикатором того, насколько хорошо соответствующее измерение дискриминирует кластеры.

Источник: "biometrica.tomsk.ru"

Классификация объектов по характеризующим их признакам

Кластерный анализ (cluster analysis) – совокупность многомерных статистических методов классификации объектов по характеризующим их признакам, разделение совокупности объектов на однородные группы, близкие по определяющим критериям, выделение объектов определенной группы.

Кластер – это группы объектов, выделенные в результате кластерного анализа на основе заданной меры сходства или различий между объектами. Объект – это конкретные предметы исследования, которые необходимо классифицировать. Объектами при классификации выступают, как правило, наблюдения. Например, потребители продукции, страны или регионы, товары и т.п.

Хотя можно проводить кластерный анализ и по переменным. Классификация объектов в многомерном кластерном анализе происходит по нескольким признакам одновременно.Это могут быть как количественные, так и категориальные переменные в зависимости от метода кластерного анализа. Итак, главная цель кластерного анализа – нахождение групп схожих объектов в выборке.

Совокупность многомерных статистических методов кластерного анализа можно разделить на иерархические методы (агломеративные и дивизимные) и неиерархические (метод k-средних, двухэтапный кластерный анализ).

Однако общепринятой классификации методов не существует, и к методам кластерного анализа иногда относят также методы построения деревьев решений, нейронных сетей, дискриминантного анализа, логистической регрессии.

Сфера использования кластерного анализа, из-за его универсальности, очень широка. Кластерный анализ применяют в экономике, маркетинге, археологии, медицине, психологии, химии, биологии, государственном управлении, филологии, антропологии, социологии и других областях.

Вот несколько примеров применения кластерного анализа:

• медицина – классификация заболеваний, их симптомов, способов лечения, классификация групп пациентов;
• маркетинг – задачи оптимизации ассортиментной линейки компании, сегментация рынка по группам товаров или потребителей, определение потенциального потребителя;
• социология – разбиение респондентов на однородные группы;
• психиатрия – корректная диагностика групп симптомов является решающей для успешной терапии;
• биология – классификация организмов по группе;
• экономика – классификация субъектов РФ по инвестиционной привлекательности.

Источник: "statmethods.ru"

Общие сведения о кластерном анализе

Кластерный анализ включает в себя набор различных алгоритмов классификации. Общий вопрос, задаваемый исследователями во многих областях, состоит в том, как организовать наблюдаемые данные в наглядные структуры.

Например, биологи ставят цель разбить животных на различные виды, чтобы содержательно описать различия между ними.

Задача кластерного анализа состоит в разбиении исходной совокупности объектов на группы схожих, близких между собой объектов. Эти группы называют кластерами.

Другими словами, кластерный анализ – это один из способов классификации объектов по их признакам. Желательно, чтобы результаты классификации имели содержательную интерпретацию.

Результаты, полученные методами кластерного анализа, применяют в самых различных областях:

1. В маркетинге – это сегментация конкурентов и потребителей.
2. В психиатрии для успешной терапии является решающей правильная диагностика симптомов, таких как паранойя, шизофрения и т.д.
3. В менеджменте важна классификация поставщиков, выявление схожих производственных ситуаций, при которых возникает брак.
4. В социологии – разбиение респондентов на однородные группы.
5. В портфельном инвестировании важно сгруппировать ценные бумаги по сходству в тенденции доходности, чтобы составить на основе полученных сведений о фондовом рынке оптимального инвестиционного портфеля, позволяющего максимизировать прибыль от вложений при заданной степени риска.

По сути, кластерный анализ хорошо зарекомендовал себя во всех сферах жизнедеятельности человека. В общем, всякий раз, когда необходимо классифицировать большое количество информации такого рода и представлять ее в виде, пригодном для дальнейшей обработки, кластерный анализ оказывается весьма полезным и эффективным.

Кластерный анализ позволяет рассматривать достаточно большой объем информации и сильно сжимать большие массивы социально-экономической информации, делать их компактными и наглядными.

Большое значение кластерный анализ имеет применительно к совокупностям временных рядов, характеризующих экономическое развитие (например, общехозяйственной и товарной конъюнктуры).

Здесь можно выделять периоды, когда значения соответствующих показателей были достаточно близкими, а также определять группы временных рядов, динамика которых наиболее схожа. В задачах социально-экономического прогнозирования весьма перспективно сочетание кластерного анализа с другими количественными методами (например, с регрессионным анализом).

Преимущества и недостатки

Кластерный анализ позволяет провести объективную классификацию любых объектов, которые охарактеризованы рядом признаков. Из этого можно извлечь ряд преимуществ:

• Полученные кластеры можно интерпретировать, то есть описывать, какие же собственно группы существуют.
• Отдельные кластеры можно выбраковывать. Это полезно в тех случаях, когда при наборе данных допущены определенные ошибки, в результате которых значения показателей у отдельных объектов резко отклоняются. При применении кластерного анализа такие объекты попадают в отдельный кластер.
• Для дальнейшего анализа могут быть выбраны только те кластеры, которые обладают интересующими характеристиками.

Как и любой другой метод, кластерный анализ имеет определенные недостатки и ограничения. В частности:

1. состав и количество кластеров зависит от выбираемых критериев разбиения,
2. при сведении исходного массива данных к более компактному виду могут возникать определенные искажения,
3. могут теряться индивидуальные черты отдельных объектов за счет замены их характеристиками обобщенных значений параметров кластера.

Методы

В настоящее время известно более сотни разных алгоритмов кластеризации. Их разнообразие объясняется не только разными вычислительными методами, но и различными концепциями, лежащими в основе кластеризации. Дать рекомендации для выбора того или иного метода кластеризации можно только в общих чертах, а основной критерий выбора – практическая полезность результата.

В пакете Statistica реализуются следующие методы кластеризации:

• Иерархические алгоритмы – древовидная кластеризация. В основе иерархических алгоритмов лежит идея последовательной кластеризации. На начальном шаге каждый объект рассматривается как отдельный кластер. На следующем шаге некоторые из ближайших друг к другу кластеров будут объединяться в отдельный кластер.
• Метод К-средних. Этот метод используется наиболее часто. Он относится к группе так называемых эталонных методов кластерного анализа. Число кластеров К задается пользователем.
• Двухвходовое объединение. При использовании этого метода кластеризация проводится одновременно как по переменным (столбцам), так и по результатам наблюдений (строкам).

Процедура двухвходового объединения производится в тех случаях, когда можно ожидать, что одновременная кластеризация по переменным и наблюдениям даст возможность получить осмысленные результаты.

Результатами процедуры являются описательные статистики по переменным и наблюдениям, а также двумерная цветная диаграмма, на которой цветом отмечаются значения данных. По распределению цвета можно составить представление об однородных группах.

Нормирование переменных

Разбиение исходной совокупности объектов на кластеры связано с вычислением расстояний между объектами и выбора объектов, расстояние между которыми наименьшее из всех возможных. Наиболее часто используется привычное всем нам евклидово (геометрическое) расстояние. Эта метрика отвечает интуитивным представлениям о близости объектов в пространстве (как будто расстояния между объектами измерены рулеткой).

Но для данной метрики на расстояние между объектами могут сильно влиять изменения масштабов (единиц измерения). Например, если один из признаков измерен в миллиметрах, а затем его значение переведены в сантиметры, евклидово расстояние между объектами сильно изменится. Это приведет к тому, что результаты кластерного анализа могут значительно отличаться от предыдущих.

Если переменные измерены в разных единицах измерения, то требуется их предварительная нормировка, то есть преобразование исходных данных, которое переводит их в безразмерные величины.

Нормировка сильно искажает геометрию исходного пространства, что может изменить результаты кластеризации. В пакете Statistica нормировка любой переменной x выполняется по формуле:

Для этого нужно щелкнуть правой кнопкой мыши по имени переменной и в открывшемся меню выбрать последовательность команд: Fill/ Standardize Block/ Standardize Columns. Значения нормированной переменной станут равными нулю, а дисперсии – единице.

Метод К-средних в программе Statistica

Метод K-средних (K-means) разбивает множество объектов на заданное число K различных кластеров, расположенных на возможно больших расстояниях друг от друга. Обычно, когда результаты кластерного анализа методом K-средних получены, можно рассчитать средние для каждого кластера по каждому измерению, чтобы оценить, насколько кластеры различаются друг от друга.

В идеале вы должны получить сильно различающиеся средние для большинства измерений, используемых в анализе. Значения F-статистики, полученные для каждого измерения, являются другим индикатором того, насколько хорошо соответствующее измерение дискриминирует кластеры.

В качестве примера рассмотрим результаты опроса 17-ти сотрудников предприятия по удовлетворенности показателями качества служебной карьеры. В таблице даны ответы на вопросы анкеты по десятибалльной шкале (1 – минимальный балл, 10 – максимальный).

Имена переменных соответствуют ответам на следующие вопросы:

1. СЛЦ – сочетание личных целей и целей организации;
2. ОСО – ощущение справедливости в оплате труда;
3. ТБД – территориальная близость к дому;
4. ОЭБ – ощущение экономического благосостояния;
5. КР – карьерный рост;
6. ЖСР – желание сменить работу;
7. ОСБ – ощущение социального благополучия.

Используя эти данные, необходимо разделить сотрудников на группы и для каждой из них выделить наиболее эффективные рычаги управления. При этом различия между группами должны быть очевидными, а внутри группы респонденты должны быть максимально похожи.

На сегодняшний день большинство социологических опросов дает лишь процентное соотношение голосов: считается основное количество положительно ответивших, либо процент неудовлетворенных, но системно этот вопрос не рассматривают. Чаще всего опрос не показывает тенденции изменения ситуации.

Для выявления на основе данных опроса некоторых реально существующих взаимосвязей признаков и порождения на этой основе их типологии можно использовать процедуры кластерного анализа. Наличие каких-либо априорных гипотез социолога при работе процедур кластерного анализа не является необходимым условием.

В программе Statistica кластерный анализ выполняется следующим образом.

1. Создать файл данных.
2. Выбрать модуль Statistics/ Multivariable Exploratory Techniques/ Cluster Analysis. Нажать ОК, в результате чего появится диалоговое окно:

   

3. В появившемся окне выбрать метод кластеризации K-means clustering и нажать ОК.
4. В появившемся диалоговом окне необходимо установить следующие настройки:

   
   

   • Выбрать переменные кнопкой Variables.
   • Выбрать объекты кластеризации: это могут быть переменные – столбцы (Variables сolumns)), либо наблюдения – строки (Cases (Rows)). Сначала проведем кластеризацию по строкам (Cases(rows)).
   • Выбрать число кластеров.
     Этот выбор делает пользователь, исходя из собственных предположений о числе групп схожих объектов.

     При выборе количества кластеров руководствуйтесь следующим:

     1. Количество кластеров, по возможности, не должно быть слишком большим.
     2. Расстояние, на котором объединялись объекты данного кластера, должно быть, по возможности, гораздо меньше расстояния, на котором к этому кластеру присоединяется еще что-либо.
     При выборе количества кластеров чаще всего есть одновременно несколько правильных решений. Нас интересует, например, как соотносятся ответы на вопросы анкеты у рядовых сотрудников и руководства предприятия. Поэтому выбираем K=2. Для дальнейшей сегментации можно увеличивать число кластеров.
     
   • Далее необходимо выбрать начальное разбиение объектов по кластерам (Initial cluster centers). Пакет Statistica предлагает:
     1. выбрать наблюдения с максимальным расстоянием между центрами кластеров;
     2. рассортировать расстояния и выбрать наблюдения с постоянными интервалами (установка по умолчанию);
     3. взять первые наблюдения за центры и присоединять остальные объекты к ним.

     Для наших целей подходит первый вариант.

Многие алгоритмы кластеризации часто «навязывают» данным не присущую им структуру и дезориентируют исследователя. Поэтому крайне необходимо применять несколько алгоритмов кластерного анализа и делать выводы на основании общей оценки результатов работы алгоритмов

Результаты анализа можно посмотреть в появившемся диалоговом окне:

Если выбрать вкладку Graph of means, будет построен график координат центров кластеров:

Каждая ломаная линия на этом графике соответствует одному из кластеров:

• Каждое деление горизонтальной оси графика соответствует одной из переменных, включенных в анализ.
• Вертикальная ось соответствует средним значениям переменных для объектов, входящих в каждый из кластеров.

Можно отметить, что просматриваются существенные отличия в отношении двух групп людей к служебной карьере почти по все вопросам. Лишь в одном вопросе наблюдается полное единодушие – в ощущении социального благополучия (ОСБ), вернее, отсутствии такового (2,5 балла из 10).

Можно предположить, что:

1. кластер 1 отображает рабочих,
2. кластер 2 – руководство:
   • Руководители больше удовлетворены карьерным ростом (КР), сочетанием личных целей и целей организации (СЛЦ).
   • У них выше уровень ощущения экономического благосостояния (ОЭБ) и ощущения справедливости в оплате труда (ОСО).
   • Территориальная близость к дому (ТБД) волнует их меньше, чем рабочих, вероятно, из-за меньших проблем с транспортом.
   • Также у руководителей меньше желания сменить работу (ЖСР).

Несмотря на то, что работники делятся на две категории, они относительно одинаково отвечают на большинство вопросов. Другими словами, если что-то не устраивает общую группу работников, то же самое не устраивает и высшее руководство, и наоборот.

Согласование графиков позволяет сделать выводы о том, что благосостояние одной группы отражается на благосостоянии другой.

Кластер 1 не доволен территориальной близостью к дому. Данной группой является основная часть работников, которые в основном приходят на предприятие с разных сторон города. Следовательно, можно предложить главному руководству направить часть прибыли на строительство жилья для сотрудников предприятия.

Просматриваются существенные отличия в отношении двух групп людей к служебной карьере:

1. Те сотрудники, которых устраивает карьерный рост, у которых высоко совпадение личных целей и целей организации, не имеют желание сменить работу и ощущают удовлетворенность результатами труда.
2. И наоборот, сотрудников, желающих сменить работу и неудовлетворенных результатами труда, не устраивают изложенные показатели.

Высшему руководству следует обратить особое внимание на сложившуюся ситуацию.

Результаты дисперсионного анализа по каждому признаку выводятся по нажатию кнопки Analysis of variance:

Выводятся:

• суммы квадратов отклонения объектов от центров кластеров (SS Within),
• суммы квадратов отклонений между центрами кластеров (SS Between),
• значения F-статистики,
• уровни значимости р.

Для нашего примера уровни значимости для двух переменных довольно велики, что объясняется малым числом наблюдений. В полном варианте исследования, с которым можно ознакомиться в работе, гипотезы о равенстве средних для центров кластеров отклоняются на уровнях значимости меньше 0,01.

Кнопка Save classifications and distances выводит номера объектов, входящих в каждый кластер и расстояния объектов до центра каждого кластера.

Состав каждого кластера и расстояния объектов от центра

В таблице показаны номера наблюдений (CASE_NO), составляющие кластеры с номерами CLUSTER и расстояния от центра каждого кластера (DISTANCE).

Информация о принадлежности объектов к кластерам может быть записана в файл и использоваться в дальнейшем анализе. В данном примере сравнение полученных результатов с анкетами показало, что кластер 1 состоит, в основном, из рядовых работников, а кластер 2 – из менеджеров.

Таким образом, можно заметить, что при обработке результатов анкетирования кластерный анализ оказался мощным методом, позволяющим сделать выводы, к которым невозможно прийти, построив гистограмму средних или посчитав процентное соотношение удовлетворенных различными показателями качества трудовой жизни.

Древовидная кластеризация – это пример иерархического алгоритма, принцип работы которого состоит в последовательном объединении в кластер сначала самых близких, а затем и все более отдаленных друг от друга элементов. Большинство из этих алгоритмов исходит из матрицы сходства (расстояний), и каждый отдельный элемент рассматривается вначале как отдельный кластер.

После загрузки модуля кластерного анализа и выбора Joining (tree clustering), в окне ввода параметров кластеризации можно изменить следующие параметры:

1. Исходные данные (Input). Они могут быть в виде матрицы исследуемых данных (Raw data) и в виде матрицы расстояний (Distance matrix).
2. Кластеризацию (Cluster) наблюдений (Cases (raw)) или переменных (Variable (columns)), описывающих состояние объекта.
3. Меры расстояния (Distance measure). Здесь возможен выбор следующих мер:
   • евклидово расстояние (Euclidean distances),
   • квадрат Евклидова расстояния (Squared Euclidean distances),
   • расстояние городских кварталов (манхэттенское расстояние, City-block (Manhattan) distance), расстояние Чебышева (Chebychev distance metric),
   • степенное расстояние (Power…;),
   • процент несогласия (Percent disagreement).
4. Метод кластеризации (Amalgamation (linkage) rule).
   Здесь возможны следующие варианты:
   • одиночная связь (метод ближайшего соседа) (Single Linkage),
   • полная связь (метод наиболее удаленных соседей) (Complete Linkage),
   • невзвешенное попарное среднее (Unweighted pair-group average),
   • взвешенное попарное среднее (Weighted pair-group average),
   • невзвешенный центроидный метод (Unweighted pair-group centroid),
   • взвешенный центроидный метод (медиана) (Weighted pair-group centroid (median)),
   • метод Уорда (Ward’s method).

В результате кластеризации строится горизонтальная или вертикальная дендрограмма – график, на котором определены расстояния между объектами и кластерами при их последовательном объединении.

Древовидная структура графика позволяет определить кластеры в зависимости от выбранного порога – заданного расстояния между кластерами.

Кроме того, выводится матрица расстояний между исходными объектами (Distance matrix); средние и среднеквадратичные отклонения для каждого исходного объекта (Distiptive statistics). Для рассмотренного примера проведем кластерный анализ переменных с установками по умолчанию. Результирующая дендрограмма изображена на рисунке:

На вертикальной оси дендрограммы откладываются расстояния между объектами и между объектами и кластерами. Так, расстояние между переменными ОЭБ и ОСО равно пяти. Эти переменные на первом шаге объединяются в один кластер.

Горизонтальные отрезки дендрограммы проводятся на уровнях, соответствующих пороговым значениям расстояний, выбираемым для данного шага кластеризации.

Из графика видно, что вопрос «желание сменить работу» (ЖСР) образует отдельный кластер. Вообще, желание свалить куда угодно посещает всех в равной степени. Далее отдельный кластер составляет вопрос о территориальной близости к дому (ТБД).

По степени важности он стоит на втором месте, что подтверждает вывод о необходимости строительства жилья, сделанный по результатам исследования методом K-средних.

Ощущение экономического благосостояния (ОЭБ) и справедливости в оплате труда (ОСО) объединены - это блок экономических вопросов. Карьерный рост (КР) и сочетание личных целей и целей организации (СЛЦ) также объединены.

Другие методы кластеризации, а также выбор других видов расстояний не приводит к существенному изменению дендрограммы.

Результаты

1. Кластерный анализ является мощным средством разведочного анализа данных и статистических исследований в любой предметной области.
2. В программе Statistica реализованы как иерархические, так и структурные методы кластерного анализа. Преимущества этого статистического пакета обусловлены их графическими возможностями. Предусмотрены двумерные и трехмерные графические отображения полученных кластеров в пространстве исследуемых переменных, а также результаты работы иерархической процедуры группирования объектов.
3. Необходимо применять несколько алгоритмов кластерного анализа и делать выводы на основании общей оценки результатов работы алгоритмов.
4. Кластерный анализ можно считать успешным, если он выполнен разными способами, проведено сравнение результатов и найдены общие закономерности, а также найдены стабильные кластеры независимо от способа кластеризации.
5. Кластерный анализ позволяет выявить проблемные ситуации и наметить пути их решения. Следовательно, этот метод непараметрической статистики можно рассматривать как составную часть системного анализа.

На сегодняшний день разработано более сотни различных алгоритмов кластеризации. В результате применения различных методов кластеризации могут быть получены неодинаковые результаты: кластеры различной формы, различное количество или состав кластеров. Это нормально и является особенностью работы того или иного алгоритма.

Например, возможны кластеры "цепочного" типа, когда кластеры представлены длинными "цепочками", кластеры удлиненной формы и т.д., а некоторые методы могут создавать кластеры произвольной формы.

Различные методы могут стремиться создавать кластеры определенных размеров (например, малых или крупных) либо предполагать в наборе данных наличие кластеров различного размера.

Некоторые методы кластерного анализа особенно чувствительны к шумам или выбросам, другие - менее.

Полученные результаты требуют дальнейшей интерпретации, исследования и изучения свойств и характеристик объектов для возможности точного описания сформированных кластеров.

Процесс кластеризации и ее результат зависит от выбранного метода и способа определения меры расстояния.

Методы кластерного анализа можно разделить на две группы:

иерархические;

неиерархические.

Каждая из этих групп включает множество подходов и алгоритмов.

10.5.1 Иерархические методы кластерного анализа

Суть иерархической кластеризации состоит в последовательном объединении меньших кластеров в большие (агломеративные методы) или разделении больших кластеров на меньшие (дивизимные методы).

Иерархические агломеративные методы (Agglomerative Nesting, AGNES) характеризуется последовательным объединением исходных элементов и соответствующим уменьшением числа кластеров. В начале работы алгоритма все объекты являются отдельными кластерами. На первом шаге два наиболее похожих объекта объединяются в кластер. На последующих шагах объединение продолжается до тех пор, пока все объекты не будут составлять один кластер.

Иерархические дивизимные (делимые) методы (DIvisive ANAlysis, DIANA) являются логической противоположностью агломеративным методам. В начале работы алгоритма все объекты принадлежат одному кластеру, который на последующих шагах делится на меньшие кластеры, в результате образуется последовательность расщепляющих групп.

Сущность этих методов при помощи дендрограммы иллюстрирована рис. 10.4.

Рис. 10.4 Дендрограмма агломеративных и дивизимных методов

Программная реализация алгоритмов кластерного анализа широко представлена в различных инструментах Data Mining, которые позволяют решать задачи достаточно большой размерности. Например, агломеративные методы реализованы в пакете SPSS, дивизимные методы - в пакете Statgraf.

Преимуществом иерархических методов кластеризации является их наглядность. Однако иерархические методы кластерного анализа используются при небольших объемах наборов данных.

Иерархические алгоритмы связаны с построением дендрограмм (от греческого dendron - "дерево"), которые являются результатом иерархического кластерного анализа. Дендрограмма описывает близость отдельных точек и кластеров друг к другу, представляет в графическом виде последовательность объединения (разделения) кластеров.

Дендрограмма (dendrogram) - древовидная диаграмма, содержащая уровней, каждый из которых соответствует одному из шагов процесса последовательного укрупнения кластеров.Дендрограмму также называют древовидной схемой, деревом объединения кластеров, деревом иерархической структуры. Дендрограмма представляет собой вложенную группировку объектов, которая изменяется на различных уровнях иерархии.

Существует много способов построения дендрограмм. В дендрограмме объекты могут располагаться вертикально или горизонтально. Пример горизонтальной дендрограммы приведен на рис. 10.4, вертикальной дендрограммы - на рис. 10.5.

Рис. 10.5. Вертикальная дендрограмма

На рис 10.5 на первом шаге каждое наблюдение представляет один кластер (вертикальная линия), на втором шаге наблюдаем объединение таких наблюдений: 11 и 10; 3, 4 и 5; 8 и 9; 2 и 6. На втором шаге продолжается объединение в кластеры: наблюдения 11, 10, 3, 4, 5 и 7, 8, 9. Данный процесс продолжается до тех пор, пока все наблюдения не объединятся в один кластер.

Объединение осуществляется с использованием одного из методов, рассмотренных в п.10.4: метод ближнего соседа, метод удаленного соседа, метод Варда, метод попарного среднего, центроидный метод и пр.