Doğrusal olarak bağımlı ve doğrusal olarak bağımsız vektörler

Görev 1. Vektör sisteminin doğrusal bağımsız olup olmadığını öğrenin. Vektör sistemi, sütunları vektörlerin koordinatlarından oluşan sistemin matrisi tarafından belirlenecektir.

.

Çözüm. Doğrusal kombinasyona izin verin sıfıra eşittir. Bu eşitliği koordinatlarda yazdıktan sonra aşağıdaki denklem sistemini elde ederiz:

.

Böyle bir denklem sistemine üçgen denir. Onun tek karar . Bu nedenle vektörler Doğrusal bağımsız.

Görev 2. Vektör sisteminin doğrusal bağımsız olup olmadığını öğrenin.

.

Çözüm. Vektörler doğrusal bağımsız (bkz. problem 1). Vektörün, vektörlerin doğrusal birleşimi olduğunu kanıtlayalım. . Vektör genişleme katsayıları denklem sisteminden belirlenir

.

Bu sistemin üçgen gibi benzersiz bir çözümü var.

Bu nedenle vektör sistemi doğrusal bağımlı.

Yorum. Problem 1'deki ile aynı tipteki matrislere denir. üçgensel ve problem 2'de – kademeli üçgen . Bir vektör sisteminin doğrusal bağımlılığı sorunu, bu vektörlerin koordinatlarından oluşan matris adım üçgen ise kolayca çözülür. Matrisin özel bir formu yoksa, o zaman kullanılır. temel dize dönüşümleri Sütunlar arasındaki doğrusal ilişkiler korunarak basamaklı üçgen forma indirgenebilir.

Temel dize dönüşümleri Matrisler (EPS) Bir matris üzerinde aşağıdaki işlemlere denir:

1) dizelerin yeniden düzenlenmesi;

2) bir dizgiyi sıfır olmayan bir sayıyla çarpmak;

3) bir dizeye rastgele bir sayıyla çarpılarak başka bir dize eklemek.

Görev 3. Maksimum doğrusal bağımsız alt sistemi bulun ve vektörler sisteminin sıralamasını hesaplayın

.

Çözüm. Sistemin matrisini EPS kullanarak basamaklı üçgen forma indirgeyelim. Prosedürü açıklamak için dönüştürülecek matrisin numarasının bulunduğu satırı sembolüyle belirtiyoruz. Oktan sonraki sütun, yeni matrisin satırlarını elde etmek için dönüştürülmekte olan matrisin satırları üzerindeki eylemleri gösterir.

.

Açıkçası, ortaya çıkan matrisin ilk iki sütunu doğrusal olarak bağımsızdır, üçüncü sütun bunların doğrusal birleşimidir ve dördüncüsü ilk ikisine bağlı değildir. Vektörler temel denir. Sistemin maksimum doğrusal olarak bağımsız bir alt sistemini oluştururlar. ve sistemin rütbesi üçtür.

Temel, koordinatlar

Görev 4. Koordinatları koşulu karşılayan geometrik vektörler kümesinde bu tabandaki vektörlerin tabanını ve koordinatlarını bulun. .

Çözüm. Küme orijinden geçen bir düzlemdir. Bir düzlemdeki keyfi bir temel, doğrusal olmayan iki vektörden oluşur. Seçilen bazdaki vektörlerin koordinatları, karşılık gelen doğrusal denklem sisteminin çözülmesiyle belirlenir.

Koordinatları kullanarak temeli bulabileceğinizde bu sorunu çözmenin başka bir yolu var.

Koordinatlar uzaylar düzlemdeki koordinatlar değildir, çünkü bunlar ilişkiyle ilişkilidir yani bağımsız değillerdir. Bağımsız değişkenler (serbest olarak adlandırılırlar) düzlemdeki bir vektörü benzersiz bir şekilde tanımlarlar ve bu nedenle de koordinatlar olarak seçilebilirler. Daha sonra temel serbest değişken kümelerinin içinde yer alan ve bunlara karşılık gelen vektörlerden oluşur Ve , yani .

Görev 5. Tek koordinatları birbirine eşit olan uzaydaki tüm vektörler kümesinde bu tabandaki vektörlerin tabanını ve koordinatlarını bulun.

Çözüm. Önceki problemde olduğu gibi uzaydaki koordinatları seçelim.

Çünkü , ardından serbest değişkenler vektörü benzersiz bir şekilde belirler ve bu nedenle koordinatlardır. Karşılık gelen taban vektörlerden oluşur.

Görev 6. Formun tüm matrisleri kümesinde bu temelde vektörlerin temelini ve koordinatlarını bulun , Nerede – keyfi sayılar.

Çözüm. Her matris aşağıdaki biçimde benzersiz bir şekilde temsil edilebilir:

Bu ilişki vektörün tabana göre açılımıdır.
koordinatlarla .

Görev 7. Bir vektör sisteminin doğrusal gövdesinin boyutunu ve tabanını bulun

.

Çözüm. EPS'yi kullanarak matrisi sistem vektörlerinin koordinatlarından adım üçgen formuna dönüştürüyoruz.

.

Sütunlar son matrisler doğrusal olarak bağımsızdır ve sütunlar bunlar aracılığıyla doğrusal olarak ifade edilir. Bu nedenle vektörler bir temel oluşturmak , Ve .

Yorum. Temel belirsiz bir şekilde seçilmiştir. Örneğin, vektörler aynı zamanda bir temel oluşturur .

Bir vektörler sisteminin doğrusal olarak bağımlı olup olmadığını kontrol etmek için, bu vektörlerin doğrusal bir kombinasyonunu oluşturmak ve en az bir katsayı sıfıra eşitse sıfır olup olamayacağını kontrol etmek gerekir.

Durum 1. Bir vektör sistemi vektörlerle verilmektedir

Doğrusal bir kombinasyon oluşturma

Homojen bir denklem sistemi elde ettik. Sıfırdan farklı bir çözümü varsa determinantın sıfıra eşit olması gerekir. Bir determinant oluşturup değerini bulalım.

Determinant sıfır olduğundan vektörler doğrusal olarak bağımlıdır.

Durum 2. Vektör sistemi analitik fonksiyonlarla tanımlanır:

A)
Eğer özdeşlik doğruysa sistem doğrusal bağımlıdır.

Doğrusal bir kombinasyon yapalım.

Bu ifadenin sıfıra eşit olduğu a, b, c (en az biri sıfıra eşit olmayan) olup olmadığını kontrol etmek gerekir.

Hiperbolik fonksiyonları yazalım

,
, Daha sonra

o zaman vektörlerin doğrusal kombinasyonu şu şekli alacaktır:

Nerede
örneğin, doğrusal kombinasyonun sıfır olduğunu, dolayısıyla sistemin doğrusal olarak bağımlı olduğunu ele alalım.

Cevap: Sistem doğrusal bağımlıdır.

B)
, doğrusal bir kombinasyon yapalım

Vektörlerin doğrusal birleşimi, x'in herhangi bir değeri için sıfıra eşit olmalıdır.

Özel durumları kontrol edelim.

Vektörlerin doğrusal bir kombinasyonu, yalnızca tüm katsayıların sıfıra eşit olması durumunda sıfıra eşittir.

Bu nedenle sistem doğrusal olarak bağımsızdır.

Cevap: Sistem doğrusal bağımsızdır.

5.3. Bir temel bulun ve doğrusal çözüm uzayının boyutunu belirleyin.

Genişletilmiş bir matris oluşturalım ve onu Gauss yöntemini kullanarak yamuk formuna indirgeyelim.

Biraz temel oluşturmak için keyfi değerleri değiştirelim:

Geri kalan koordinatları alalım

Cevap:

5.4. Temelde verilmişse, X vektörünün koordinatlarını bulun.

Vektör koordinatlarını yeni bir temelde bulmak, denklem sistemini çözmek anlamına gelir

Yöntem 1. Geçiş matrisini kullanarak bulma

Bir geçiş matrisi oluşturalım

Formülü kullanarak vektörü yeni temelde bulalım.

Ters matrisi bulalım ve çarpma işlemini yapalım

,

Yöntem 2. Bir denklem sistemi oluşturarak bulma.

Temel katsayılardan temel vektörleri oluşturalım

,
,

Vektörü yeni temelde bulma şu şekildedir:

, Nerede D bu verilen bir vektör X.

Ortaya çıkan denklem herhangi bir şekilde çözülebilir, cevap benzer olacaktır.

Cevap: yeni bir temelde vektör
.

5.5. x = olsun (X 1 , X 2 , X 3 ) . Aşağıdaki dönüşümler doğrusal mıdır?

Verilen vektörlerin katsayılarından doğrusal operatörlerin matrislerini oluşturalım.

Her doğrusal operatör matrisi için doğrusal işlem özelliğini kontrol edelim.

Matrisi çarparak sol tarafı buluruz A vektöre

Verilen vektörü bir skalerle çarparak sağ tarafı buluruz
.

Bunu görüyoruz
Bu, dönüşümün doğrusal olmadığı anlamına gelir.

Diğer vektörleri kontrol edelim.

dönüşüm doğrusal değildir.

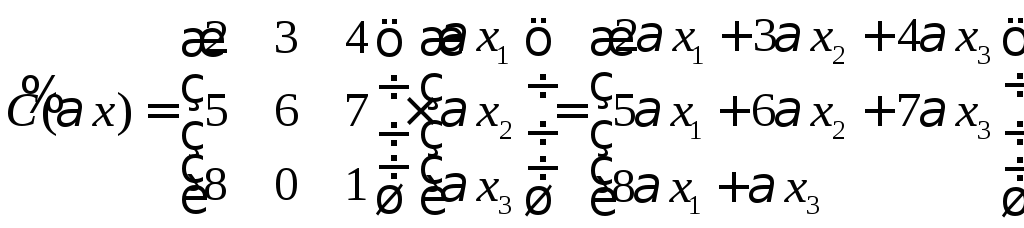
dönüşüm doğrusaldır.

Cevap: Ah– doğrusal bir dönüşüm değil, İçinde– doğrusal değil, Cx- doğrusal.

Not. Verilen vektörlere dikkatlice bakarak bu görevi çok daha kolay tamamlayabilirsiniz. İÇİNDE Ah eleman içermeyen terimlerin olduğunu görüyoruz X doğrusal bir işlem sonucunda elde edilemeyen. İÇİNDE İçinde bir unsur var X bir vektörle çarpılarak da elde edilemeyen üçüncü kuvvete X.

5.6. Verilen X = { X 1 , X 2 , X 3 } , Balta = { X 2 – X 3 , X 1 , X 1 + X 3 } , Bx = { X 2 , 2 X 3 , X 1 } . Belirtilen işlemi gerçekleştirin: ( A ( B – A )) X .

Doğrusal operatörlerin matrislerini yazalım.

Matrisler üzerinde bir işlem yapalım

Ortaya çıkan matrisi X ile çarptığımızda şunu elde ederiz:

Cevap:

Tanım. Vektörlerin doğrusal kombinasyonu a 1 , ..., katsayıları x 1 , ..., x n olan bir n'ye vektör denir

x 1 a 1 + ... + x n a n .

önemsiz, eğer tüm katsayılar x 1 , ..., x n sıfıra eşitse.

Tanım. x 1 a 1 + ... + x n an n doğrusal kombinasyonuna denir önemsiz değil, x 1, ..., x n katsayılarından en az biri sıfıra eşit değilse.

Doğrusal bağımsız, eğer bu vektörlerin sıfır vektörüne eşit önemsiz olmayan bir kombinasyonu yoksa.

Yani, a 1, ..., a n vektörleri eğer x 1 a 1 + ... + x n a n = 0 ise ancak ve ancak x 1 = 0, ..., x n = 0 ise doğrusal olarak bağımsızdır.

Tanım. a 1, ..., a n vektörlerine denir doğrusal bağımlı, eğer bu vektörlerin sıfır vektörüne eşit önemsiz olmayan bir kombinasyonu varsa.

Doğrusal bağımlı vektörlerin özellikleri:

2 ve 3 boyutlu vektörler için.

Doğrusal olarak bağımlı iki vektör eşdoğrusaldır. (Doğrusal vektörler doğrusal olarak bağımlıdır.)

3 boyutlu vektörler için.

Doğrusal olarak bağımlı üç vektör aynı düzlemdedir. (Üç eş düzlemli vektör doğrusal olarak bağımlıdır.)

• N boyutlu vektörler için.

  n + 1 vektör her zaman doğrusal olarak bağımlıdır.

Vektörlerin doğrusal bağımlılığı ve doğrusal bağımsızlığı ile ilgili problem örnekleri:

Örnek 1. a = (3; 4; 5), b = (-3; 0; 5), c = (4; 4; 4), d = (3; 4; 0) vektörlerinin doğrusal olarak bağımsız olup olmadığını kontrol edin. .

Çözüm:

Vektörlerin boyutu vektör sayısından az olduğundan vektörler doğrusal olarak bağımlı olacaktır.

Örnek 2. a = (1; 1; 1), b = (1; 2; 0), c = (0; -1; 1) vektörlerinin doğrusal olarak bağımsız olup olmadığını kontrol edin.

Çözüm:

	x 1 + x 2 = 0
	x 1 + 2x 2 - x 3 = 0
	x 1 + x 3 = 0

	1	1	0	0		~
	1	2	-1	0
	1	0	1	0

~		1	1	0	0		~		1	1	0	0		~
		1 - 1	2 - 1	-1 - 0	0 - 0				0	1	-1	0
		1 - 1	0 - 1	1 - 0	0 - 0				0	-1	1	0

ikinciyi birinci satırdan çıkarın; üçüncü satıra ikinci satırı ekleyin:

~		1 - 0	1 - 1	0 - (-1)	0 - 0		~		1	0	1	0
		0	1	-1	0				0	1	-1	0
		0 + 0	-1 + 1	1 + (-1)	0 + 0				0	0	0	0

Bu çözüm, sistemin birçok çözümü olduğunu, yani a, b, c vektörlerinin doğrusal kombinasyonunun eşit olacağı şekilde x 1, x 2, x 3 sayılarının değerlerinin sıfır olmayan bir kombinasyonunun olduğunu gösterir. sıfır vektörü, örneğin:

bir + b + c = 0

bu, a, b, c vektörlerinin doğrusal olarak bağımlı olduğu anlamına gelir.

Cevap: a, b, c vektörleri doğrusal olarak bağımlıdır.

Örnek 3. a = (1; 1; 1), b = (1; 2; 0), c = (0; -1; 2) vektörlerinin doğrusal olarak bağımsız olup olmadığını kontrol edin.

Çözüm: Bu vektörlerin doğrusal birleşiminin sıfır vektörüne eşit olacağı katsayıların değerlerini bulalım.

x 1 a + x 2 b + x 3 c 1 = 0

Bu vektör denklemi bir doğrusal denklem sistemi olarak yazılabilir.

	x 1 + x 2 = 0
	x 1 + 2x 2 - x 3 = 0
	x 1 + 2x 3 = 0

Bu sistemi Gauss yöntemini kullanarak çözelim

	1	1	0	0		~
	1	2	-1	0
	1	0	2	0

birincisini ikinci satırdan çıkarın; birincisini üçüncü satırdan çıkarın:

~		1	1	0	0		~		1	1	0	0		~
		1 - 1	2 - 1	-1 - 0	0 - 0				0	1	-1	0
		1 - 1	0 - 1	2 - 0	0 - 0				0	-1	2	0

ikinciyi birinci satırdan çıkarın; üçüncü satıra bir saniye ekleyin.

Doğrusal bağımlılık Ve doğrusal bağımsızlık vektörler.
Vektörlerin temeli. Afin koordinat sistemi

Oditoryumda çikolatalarla dolu bir araba var ve bugün her ziyaretçi tatlı bir çiftle karşılaşacak: analitik geometri ve doğrusal cebir. Bu makale yüksek matematiğin iki bölümüne aynı anda değinecek ve bunların tek bir pakette nasıl bir arada var olduklarını göreceğiz. Biraz ara verin, bir Twix yiyin! ...kahretsin, ne kadar saçmalık. Her ne kadar tamam, puan vermeyeceğim, sonuçta çalışmaya karşı olumlu bir tutuma sahip olmalısınız.

Vektörlerin doğrusal bağımlılığı, doğrusal vektör bağımsızlığı, vektör temeli ve diğer terimlerin yalnızca geometrik bir yorumu değil, her şeyden önce cebirsel bir anlamı vardır. Doğrusal cebir açısından "vektör" kavramı her zaman bir düzlemde veya uzayda tasvir edebileceğimiz "sıradan" bir vektör değildir. Kanıt için çok uzaklara bakmanıza gerek yok, beş boyutlu uzayın vektörünü çizmeyi deneyin . Veya az önce Gismeteo'ya gittiğim hava durumu vektörü: – sıcaklık ve Atmosfer basıncı sırasıyla. Örnek, elbette, vektör uzayının özellikleri açısından yanlıştır, ancak yine de hiç kimse bu parametrelerin bir vektör olarak resmileştirilmesini yasaklamaz. Sonbaharın nefesi...

Hayır, sizi teoriyle, doğrusal vektör uzaylarıyla sıkmayacağım. anlamak Tanımlar ve teoremler. Yeni terimler (doğrusal bağımlılık, bağımsızlık, doğrusal kombinasyon, temel vb.) cebirsel açıdan tüm vektörler için geçerlidir ancak geometrik örnekler verilecektir. Böylece her şey basit, erişilebilir ve anlaşılır. Analitik geometri problemlerine ek olarak bazı tipik cebir problemlerini de ele alacağız. Materyalde ustalaşmak için derslere aşina olmanız tavsiye edilir. Aptallar için vektörler Ve Determinant nasıl hesaplanır?

Düzlem vektörlerin doğrusal bağımlılığı ve bağımsızlığı.
Düzlem temeli ve afin koordinat sistemi

Uçağınızı düşünün bilgisayar masası(sadece bir masa, komodin, zemin, tavan, ne istersen). Görev aşağıdaki eylemlerden oluşacaktır:

1) Düzlem tabanını seçin. Kabaca söylemek gerekirse, bir masa tablasının uzunluğu ve genişliği vardır, dolayısıyla temeli oluşturmak için iki vektörün gerekli olacağı sezgiseldir. Bir vektör kesinlikle yeterli değil, üç vektör çok fazla.

2) Seçilen esasa göre koordinat sistemini ayarla(koordinat ızgarası) tablodaki tüm nesnelere koordinatlar atamak için kullanılır.

Şaşırmayın, ilk başta açıklamalar parmaklarda kalacak. Üstelik seninkinde. Lütfen yerleştirin sol işaret parmağı monitöre bakması için masanın kenarına. Bu bir vektör olacak. Şimdi yer Serçe parmak sağ el aynı şekilde masanın kenarında - monitör ekranına doğru yönlendirilecek şekilde. Bu bir vektör olacak. Gülümse, harika görünüyorsun! Vektörler hakkında ne söyleyebiliriz? Veri vektörleri doğrusal, yani doğrusal birbirleriyle ifade edilir:
, peki, ya da tam tersi: burada sıfırdan farklı bir sayı var.

Bu eylemin bir resmini sınıfta görebilirsiniz. Aptallar için vektörler Burada bir vektörü bir sayıyla çarpma kuralını açıkladım.

Parmaklarınız bilgisayar masasının düzlemine temel oluşturacak mı? Belli ki değil. Doğrusal vektörler ileri geri hareket eder yalnız yönü vardır ve bir düzlemin uzunluğu ve genişliği vardır.

Bu tür vektörlere denir doğrusal bağımlı.

Referans: “Doğrusal”, “doğrusal” kelimeleri, matematiksel denklemlerde ve ifadelerde kare, küp, diğer kuvvetler, logaritma, sinüs vb. bulunmadığını ifade eder. Yalnızca doğrusal (1. derece) ifadeler ve bağımlılıklar vardır.

İki düzlem vektörü doğrusal bağımlı ancak ve ancak eşdoğrusal olmaları durumunda.

Parmaklarınızı masanın üzerinde aralarında 0 veya 180 derece dışında herhangi bir açı olacak şekilde çaprazlayın. İki düzlem vektörüdoğrusal Olumsuz bağımlı ancak ve ancak eşdoğrusal değillerse. Böylece temel elde edilmiş olur. Temelin farklı uzunluklarda dik olmayan vektörlerle “çarpık” olduğu ortaya çıkmasından utanmanıza gerek yok. Çok yakında, yapımı için yalnızca 90 derecelik bir açının uygun olmadığını ve yalnızca eşit uzunluktaki birim vektörlerin uygun olmadığını göreceğiz.

Herhangi düzlem vektör tek yol esasına göre genişletilir:
, gerçek sayılar nerede. Numaralar denir vektör koordinatları bu temelde.

Ayrıca söyleniyor ki vektörolarak sunuldu doğrusal kombinasyon temel vektörleri. Yani ifade denir vektör ayrışmasıtemelde veya doğrusal kombinasyon temel vektörler.

Örneğin, vektörün düzlemin ortonormal bazında ayrıştırıldığını veya vektörlerin doğrusal bir birleşimi olarak temsil edildiğini söyleyebiliriz.

Hadi formüle edelim temelin tanımı resmi olarak: Uçağın temeli doğrusal olarak bağımsız (doğrusal olmayan) vektör çifti olarak adlandırılır, , burada herhangi bir düzlem vektörü temel vektörlerin doğrusal bir birleşimidir.

Tanımın önemli bir noktası, vektörlerin alınmış olmasıdır. belli bir sırayla. Üsler – bunlar tamamen farklı iki temel! Dedikleri gibi, sağ elinizin küçük parmağının yerine sol elinizin küçük parmağını koyamazsınız.

Temelini çözdük ama bilgisayar masanızdaki her öğeye bir koordinat ızgarası ayarlamak ve koordinatları atamak yeterli değil. Neden yeterli değil? Vektörler serbesttir ve tüm düzlem boyunca dolaşırlar. Peki, çılgın bir hafta sonundan kalan masadaki o küçük kirli noktalara koordinatları nasıl atarsınız? Bir başlangıç ​​noktasına ihtiyaç var. Ve böyle bir dönüm noktası, herkesin bildiği bir noktadır - koordinatların kökeni. Koordinat sistemini anlayalım:

“Okul” sistemiyle başlayacağım. Zaten giriş dersinde Aptallar için vektörler Dikdörtgen koordinat sistemi ile ortonormal taban arasındaki bazı farklılıkların altını çizdim. İşte standart resim:

Onlar hakkında konuştuklarında dikdörtgen koordinat sistemi, o zaman çoğu zaman orijin, koordinat eksenleri ve eksenler boyunca ölçek anlamına gelir. Bir arama motoruna “dikdörtgen koordinat sistemi” yazmayı deneyin; birçok kaynağın size 5-6. Sınıflardan aşina olduğunuz koordinat eksenlerini ve düzlemdeki noktaların nasıl çizileceğini anlatacağını göreceksiniz.

Öte yandan, dikdörtgen bir koordinat sisteminin tamamen ortonormal bir temele göre tanımlanabileceği görülmektedir. Ve bu neredeyse doğru. İfade şu şekildedir:

Menşei, Ve ortonormal temel belirlendi Kartezyen dikdörtgen düzlem koordinat sistemi . Yani dikdörtgen koordinat sistemi kesinlikle tek bir nokta ve iki birim dik vektörlerle tanımlanır. Bu yüzden yukarıda verdiğim çizimi görüyorsunuz - geometrik problemlerde hem vektörler hem de koordinat eksenleri sıklıkla (ancak her zaman değil) çizilir.

Sanırım herkes bir nokta (köken) ve ortonormal temel kullanmanın bunu anladığını düşünüyorum. Düzlemdeki HERHANGİ BİR NOKTA ve düzlemdeki HERHANGİ BİR VEKTÖR koordinatlar atanabilir. Mecazi anlamda konuşursak, "bir düzlemdeki her şey numaralandırılabilir."

Koordinat vektörlerinin birim olması gerekiyor mu? Hayır, sıfır olmayan isteğe bağlı bir uzunluğa sahip olabilirler. Sıfır olmayan uzunlukta keyfi bir nokta ve iki dik vektör düşünün:

Böyle bir temel denir dikey. Vektörlerle koordinatların kökeni bir koordinat ızgarası ile tanımlanır ve düzlemdeki herhangi bir noktanın, herhangi bir vektörün belirli bir temelde koordinatları vardır. Örneğin veya. Bariz rahatsızlık, koordinat vektörlerinin Genel olarak birlik dışında farklı uzunluklara sahiptir. Uzunluklar bire eşitse olağan ortonormal taban elde edilir.

! Not : ortogonal temelde ve düzlem ve uzayın afin tabanlarında eksenler boyunca birimler dikkate alınır ŞARTLI. Örneğin, x ekseni boyunca bir birim 4 cm, ordinat ekseni boyunca bir birim 2 cm içerir. Bu bilgi, gerekirse "standart olmayan" koordinatları "her zamanki santimetremize" dönüştürmek için yeterlidir.

Aslında zaten yanıtlanmış olan ikinci soru ise temel vektörler arasındaki açının 90 dereceye eşit olup olmaması gerektiğidir. HAYIR! Tanımda belirtildiği gibi temel vektörler şu şekilde olmalıdır: yalnızca doğrusal olmayan. Buna göre açı 0 ile 180 derece dışında herhangi bir değer olabilir.

Uçakta adı verilen bir nokta Menşei, Ve doğrusal olmayan vektörler, , ayarlamak afin düzlem koordinat sistemi :

Bazen böyle bir koordinat sistemine denir eğik sistem. Örnek olarak çizimde noktalar ve vektörler gösterilmektedir:

Anladığınız gibi afin koordinat sistemi daha da az kullanışlıdır; dersin ikinci bölümünde tartıştığımız vektörlerin ve bölümlerin uzunluklarına ilişkin formüller bu sistemde çalışmıyor. Aptallar için vektörler ile ilgili birçok lezzetli formül vektörlerin skaler çarpımı. Ancak vektörleri toplama ve bir vektörü bir sayıyla çarpma kuralları, bu ilişkide bir parçayı bölme formülleri ve yakında ele alacağımız diğer bazı problem türleri geçerlidir.

Ve sonuç şu ki, afin koordinat sisteminin en uygun özel durumu Kartezyen dikdörtgen sistemdir. Bu yüzden onu sık sık görmen gerekiyor canım. ...Ancak, bu hayatta her şey görecelidir; eğik bir açının (ya da örneğin başka bir açının) olduğu pek çok durum vardır. kutupsal) koordinat sistemi. Ve insansılar bu tür sistemleri sevebilir =)

Pratik kısma geçelim. Bu dersteki tüm problemler hem dikdörtgen koordinat sistemi hem de genel afin durum için geçerlidir. Burada karmaşık bir şey yok; tüm materyallere bir okul çocuğu bile erişebilir.

Düzlem vektörlerin doğrusallığı nasıl belirlenir?

Tipik bir şey. İki düzlem vektörü için eşdoğrusal olsaydı, karşılık gelen koordinatlarının orantılı olması gerekli ve yeterliydi Aslında bu, bariz ilişkinin koordinat bazında detaylandırılmasıdır.

örnek 1

a) Vektörlerin doğrusal olup olmadığını kontrol edin .
b) Vektörler bir taban oluşturuyor mu? ?

Çözüm:
a) Vektörler için var olup olmadığını bulalım. eşitlikler sağlanacak şekilde orantı katsayısı:

Pratikte oldukça işe yarayan bu kuralı uygulamanın “züppece” versiyonunu size mutlaka anlatacağım. Buradaki fikir, hemen oranı telafi etmek ve doğru olup olmadığına bakmaktır:

Vektörlerin karşılık gelen koordinatlarının oranlarından bir orantı kuralım:

Kısaltalım:
dolayısıyla karşılık gelen koordinatlar orantılıdır, bu nedenle,

İlişki tam tersi şekilde de yapılabilir; bu da eşdeğer bir seçenektir:

Kendi kendini test etmek için eşdoğrusal vektörlerin birbirleri aracılığıyla doğrusal olarak ifade edildiği gerçeğini kullanabilirsiniz. İÇİNDE bu durumda eşitlikler var . Geçerlilikleri, vektörlerle yapılan temel işlemlerle kolayca doğrulanabilir:

b) İki düzlem vektörü eşdoğrusal (doğrusal olarak bağımsız) değillerse bir temel oluştururlar. Doğrusallık açısından vektörleri inceliyoruz . Bir sistem oluşturalım:

İlk denklemden şu çıkıyor, ikinci denklemden şu çıkıyor, yani sistem tutarsız(çözüm yok). Dolayısıyla vektörlerin karşılık gelen koordinatları orantılı değildir.

Çözüm: vektörler doğrusal olarak bağımsızdır ve bir temel oluşturur.

Çözümün basitleştirilmiş bir versiyonu şuna benzer:

Vektörlerin karşılık gelen koordinatlarından bir orantı kuralım :
Bu, bu vektörlerin doğrusal olarak bağımsız olduğu ve bir temel oluşturduğu anlamına gelir.

Genellikle bu seçenek incelemeciler tarafından reddedilmez, ancak bazı koordinatların sıfıra eşit olduğu durumlarda sorun ortaya çıkar. Bunun gibi: . Veya bunun gibi: . Veya bunun gibi: . Burada orantı nasıl çalışılır? (aslında sıfıra bölemezsiniz). Bu nedenle basitleştirilmiş çözüme "züppe" adını verdim.

Cevap: a) , b) şeklinde.

Küçük bir yaratıcı örnek bağımsız karar:

Örnek 2

Vektörler parametrenin hangi değerindedir? doğrusal olacaklar mı?

Örnek çözümde parametre orantı yoluyla bulunur.

Vektörleri doğrusallık açısından kontrol etmenin zarif bir cebirsel yolu var. Bilgimizi sistematize edelim ve bunu beşinci nokta olarak ekleyelim:

İki düzlem vektör için aşağıdaki ifadeler eşdeğerdir:

2) vektörler bir temel oluşturur;
3) vektörler eşdoğrusal değildir;

+ 5) Bu vektörlerin koordinatlarından oluşan determinant sıfırdan farklıdır.

Sırasıyla, aşağıdaki zıt ifadeler eşdeğerdir:
1) vektörler doğrusal olarak bağımlıdır;
2) vektörler bir temel oluşturmaz;
3) vektörler doğrusaldır;
4) vektörler birbirleri aracılığıyla doğrusal olarak ifade edilebilir;
+ 5) Bu vektörlerin koordinatlarından oluşan determinant sıfıra eşittir.

Gerçekten, gerçekten bunu umuyorum şu an Karşılaştığınız tüm terimleri ve ifadeleri zaten anlıyorsunuz.

Yeni beşinci noktaya daha yakından bakalım: iki düzlem vektörleri ancak ve ancak verilen vektörlerin koordinatlarından oluşan determinantın sıfıra eşit olması durumunda eşdoğrusaldırlar:. Bu özelliği uygulamak için elbette şunları yapabilmeniz gerekir: belirleyicileri bul.

Haydi karar verelimÖrnek 1 ikinci şekilde:

a) Vektörlerin koordinatlarından oluşan determinantı hesaplayalım. :
Bu, bu vektörlerin doğrusal olduğu anlamına gelir.

b) İki düzlem vektörü eşdoğrusal (doğrusal olarak bağımsız) değillerse bir temel oluştururlar. Vektör koordinatlarından oluşan determinantı hesaplayalım :
Bu, vektörlerin doğrusal olarak bağımsız olduğu ve bir temel oluşturduğu anlamına gelir.

Cevap: a) , b) şeklinde.

Orantılı bir çözümden çok daha kompakt ve daha güzel görünüyor.

Ele alınan malzemenin yardımıyla, yalnızca vektörlerin eşdoğrusallığını oluşturmak değil, aynı zamanda parçaların ve düz çizgilerin paralelliğini de kanıtlamak mümkündür. Belirli geometrik şekillerle ilgili birkaç problemi ele alalım.

Örnek 3

Bir dörtgenin köşeleri verilmiştir. Dörtgenin paralelkenar olduğunu kanıtlayın.

Kanıt: Çözüm tamamen analitik olacağından problemde çizim oluşturmaya gerek yoktur. Paralelkenarın tanımını hatırlayalım:
Paralelkenar Karşılıklı kenarları paralel olan çiftlere dörtgen denir.

Bu nedenle aşağıdakileri kanıtlamak gerekir:
1) karşıt tarafların paralelliği ve;
2) karşıt tarafların paralelliği ve.

Kanıtlıyoruz:

1) Vektörleri bulun:

2) Vektörleri bulun:

Sonuç aynı vektördür (“okula göre” - eşit vektörler). Eşdoğrusallık oldukça açıktır, ancak kararı düzenlemeyle net bir şekilde resmileştirmek daha iyidir. Vektör koordinatlarından oluşan determinantı hesaplayalım:
, bu, bu vektörlerin eşdoğrusal olduğu anlamına gelir ve .

Çözüm: Bir dörtgenin karşılıklı kenarları çiftler halinde paraleldir, bu da tanımı gereği bir paralelkenar olduğu anlamına gelir. Q.E.D.

Daha iyi ve farklı rakamlar:

Örnek 4

Bir dörtgenin köşeleri verilmiştir. Dörtgenin yamuk olduğunu kanıtlayın.

Kanıtın daha titiz bir formülasyonu için, elbette yamuğun tanımını almak daha iyidir, ancak neye benzediğini hatırlamak yeterlidir.

Bu sizin kendi başınıza çözmeniz gereken bir görevdir. Tam çözüm dersin sonunda.

Ve şimdi yavaş yavaş uçaktan uzaya geçme zamanı:

Uzay vektörlerinin doğrusallığı nasıl belirlenir?

Kural çok benzer. İki uzay vektörünün eşdoğrusal olabilmesi için karşılık gelen koordinatlarının orantılı olması gerekli ve yeterlidir..

Örnek 5

Aşağıdaki uzay vektörlerinin eşdoğrusal olup olmadığını öğrenin:

A) ;
B)
V)

Çözüm:
a) Vektörlerin karşılık gelen koordinatları için bir orantı katsayısı olup olmadığını kontrol edelim:

Sistemin çözümü yoktur, bu da vektörlerin doğrusal olmadığı anlamına gelir.

Oran kontrol edilerek “Basitleştirilmiş” resmileştirilir. Bu durumda:
– karşılık gelen koordinatlar orantılı değildir; bu, vektörlerin eşdoğrusal olmadığı anlamına gelir.

Cevap: vektörler eşdoğrusal değildir.

b-c) Bunlar bağımsız karar verme noktalarıdır. İki şekilde deneyin.

Üçüncü dereceden bir determinant aracılığıyla uzaysal vektörlerin eşdoğrusallık açısından kontrol edilmesi için bir yöntem vardır, Bu method makalede ele alınan Vektörlerin vektör çarpımı.

Düzlem durumuna benzer şekilde, dikkate alınan araçlar, uzaysal bölümlerin ve düz çizgilerin paralelliğini incelemek için kullanılabilir.

İkinci bölüme hoş geldiniz:

Üç boyutlu uzayda vektörlerin doğrusal bağımlılığı ve bağımsızlığı.
Uzamsal temel ve afin koordinat sistemi

Uçakta incelediğimiz desenlerin birçoğu uzay için de geçerli olacak. Bilgideki aslan payı zaten çiğnendiğinden teori notlarını en aza indirmeye çalıştım. Ancak yeni terim ve kavramlar çıkacağı için giriş kısmını dikkatli okumanızı tavsiye ederim.

Artık bilgisayar masasının düzlemi yerine üç boyutlu uzayı keşfediyoruz. Öncelikle temelini oluşturalım. Birileri artık içeride, birileri dışarıda ama her halükarda üç boyuttan kaçamıyoruz: genişlik, uzunluk ve yükseklik. Bu nedenle, bir temel oluşturmak için üç uzaysal vektör gerekli olacaktır. Bir veya iki vektör yeterli değildir, dördüncüsü gereksizdir.

Ve yine parmaklarımızda ısınıyoruz. Lütfen elinizi kaldırın ve yayın farklı taraflar başparmak, işaret parmağı ve orta parmak . Bunlar vektörler olacak, farklı yönlere bakıyorlar, farklı uzunluklara sahipler ve kendi aralarında farklı açılara sahipler. Tebrikler, üç boyutlu uzayın temeli hazır! Bu arada parmaklarınızı ne kadar çevirseniz de bunu öğretmenlere göstermenize gerek yok ama tanımlardan kaçış yok =)

Sonra kendimize önemli bir soru soralım: herhangi üç vektör üç boyutlu uzayın temelini oluşturur mu?? Lütfen üç parmağınızı bilgisayar masasının üstüne sıkıca bastırın. Ne oldu? Üç vektör aynı düzlemde yer alıyor ve kabaca konuşursak boyutlardan birini kaybettik - yükseklik. Bu tür vektörler aynı düzlemde ve üç boyutlu uzayın temelinin yaratılmadığı çok açıktır.

Eş düzlemli vektörlerin aynı düzlemde olması gerekmediğine dikkat edilmelidir, paralel düzlemlerde olabilirler (bunu parmaklarınızla yapmayın, bunu yalnızca Salvador Dali yaptı =)).

Tanım: vektörlere denir aynı düzlemde, eğer paralel oldukları bir düzlem varsa. Buraya şunu eklemek mantıklıdır: Böyle bir düzlem yoksa vektörler aynı düzlemde olmayacaktır.

Üç eş düzlemli vektör her zaman doğrusal olarak bağımlıdır yani birbirleri aracılığıyla doğrusal olarak ifade edilirler. Basitleştirmek için, yine aynı düzlemde olduklarını hayal edelim. İlk olarak, vektörler sadece eş düzlemli değildir, aynı zamanda doğrusal da olabilirler, bu durumda herhangi bir vektör herhangi bir vektör aracılığıyla ifade edilebilir. İkinci durumda, örneğin vektörler eşdoğrusal değilse, üçüncü vektör bunlar aracılığıyla benzersiz bir şekilde ifade edilir: (ve önceki bölümdeki materyallerden nedenini tahmin etmek kolaydır).

Bunun tersi de doğrudur: eş düzlemli olmayan üç vektör her zaman doğrusal olarak bağımsızdır yani hiçbir şekilde birbirleri aracılığıyla ifade edilmezler. Ve açıkçası, yalnızca bu tür vektörler üç boyutlu uzayın temelini oluşturabilir.

Tanım: Üç boyutlu uzayın temeli doğrusal olarak bağımsız (eş düzlemli olmayan) vektörlerin üçlüsü olarak adlandırılır, belli bir sıraya göre alınır ve uzayın herhangi bir vektörü tek yol belirli bir temele göre ayrıştırılır; bu temeldeki vektörün koordinatları nerededir?

Vektörün formda temsil edildiğini de söyleyebileceğimizi hatırlatmama izin verin. doğrusal kombinasyon temel vektörler.

Koordinat sistemi kavramı, düzlem durumundakiyle tamamen aynı şekilde tanıtılmıştır; bir nokta ve herhangi üç doğrusal bağımsız vektör yeterlidir:

Menşei, Ve eş düzlemli olmayan vektörler, belli bir sıraya göre alınır, ayarlamak üç boyutlu uzayın afin koordinat sistemi :

Elbette koordinat ızgarası "eğik" ve elverişsizdir, ancak yine de oluşturulan koordinat sistemi bize izin verir kesinlikle herhangi bir vektörün koordinatlarını ve uzaydaki herhangi bir noktanın koordinatlarını belirler. Daha önce bahsettiğim bazı formüller tıpkı düzlem gibi uzayın afin koordinat sisteminde çalışmayacaktır.

Herkesin tahmin ettiği gibi, afin koordinat sisteminin en tanıdık ve kullanışlı özel durumu şudur: dikdörtgen uzay koordinat sistemi:

Uzayda bir noktaya denir Menşei, Ve ortonormal temel belirlendi Kartezyen dikdörtgen uzay koordinat sistemi . Tanıdık resim:

Pratik görevlere geçmeden önce bilgileri tekrar sistematize edelim:

Üç uzay vektörü için aşağıdaki ifadeler eşdeğerdir:
1) vektörler doğrusal olarak bağımsızdır;
2) vektörler bir temel oluşturur;
3) vektörler eş düzlemli değildir;
4) vektörler birbirleri aracılığıyla doğrusal olarak ifade edilemez;
5) Bu vektörlerin koordinatlarından oluşan determinant sıfırdan farklıdır.

Zıt ifadelerin anlaşılır olduğunu düşünüyorum.

Uzay vektörlerinin doğrusal bağımlılığı/bağımsızlığı geleneksel olarak bir determinant (nokta 5) kullanılarak kontrol edilir. Geri kalan pratik görevler belirgin bir cebirsel nitelikte olacaktır. Geometri çubuğunu bir kenara bırakıp doğrusal cebir beyzbol sopasını kullanmanın zamanı geldi:

Uzayın üç vektörü ancak ve ancak verilen vektörlerin koordinatlarından oluşan determinantın sıfıra eşit olması durumunda eş düzlemlidir: .

Dikkatinizi küçük bir noktaya çekiyorum teknik nüans: Vektörlerin koordinatları yalnızca sütunlarda değil satırlarda da yazılabilir (determinantın değeri bundan değişmeyecektir - bkz. determinantların özellikleri). Ancak bazı pratik sorunların çözümünde daha faydalı olduğu için sütunlarda çok daha iyidir.

Belirleyicileri hesaplama yöntemlerini biraz unutmuş veya belki de hiç anlamayan okuyuculara en eski derslerimden birini öneriyorum: Determinant nasıl hesaplanır?

Örnek 6

Aşağıdaki vektörlerin üç boyutlu uzayın temelini oluşturup oluşturmadığını kontrol edin:

Çözüm: Aslında tüm çözüm determinantın hesaplanmasından ibarettir.

a) Vektör koordinatlarından oluşan determinantı hesaplayalım (determinant ilk satırda ortaya çıkıyor):

Bu, vektörlerin doğrusal olarak bağımsız olduğu (eş düzlemli olmadığı) ve üç boyutlu uzayın temelini oluşturduğu anlamına gelir.

Cevap: bu vektörler bir temel oluşturur

b) Bu bağımsız karar verilmesi gereken bir noktadır. Dersin sonunda tam çözüm ve cevap.

Ayrıca yaratıcı görevler de vardır:

Örnek 7

Parametrenin hangi değerinde vektörler eş düzlemli olacaktır?

Çözüm: Vektörler ancak ve ancak bu vektörlerin koordinatlarından oluşan determinantın sıfıra eşit olması durumunda eş düzlemlidir:

Temel olarak determinantı olan bir denklemi çözmeniz gerekir. Jerboalardaki uçurtmalar gibi sıfırlara saldırıyoruz - ikinci satırdaki determinantı açmak ve eksilerden hemen kurtulmak en iyisidir:

Daha fazla basitleştirmeler yapıyoruz ve konuyu en basitine indiriyoruz Doğrusal Denklem:

Cevap: saat

Burada kontrol etmek kolaydır; bunu yapmak için, elde edilen değeri orijinal determinantın yerine koymanız ve şu şekilde olduğundan emin olmanız gerekir: , tekrar açıyorum.

Sonuç olarak bir tanesine daha bakalım tipik görev doğası gereği daha cebirsel olan ve geleneksel olarak doğrusal cebir dersine dahil edilen. O kadar yaygındır ki kendi konusunu hak etmektedir:

3 vektörün üç boyutlu uzayın temelini oluşturduğunu kanıtlayın
ve bu temelde 4. vektörün koordinatlarını bulun

Örnek 8

Vektörler verilmiştir. Vektörlerin üç boyutlu uzayda bir taban oluşturduğunu gösterin ve bu tabandaki vektörün koordinatlarını bulun.

Çözüm: Öncelikle durumu ele alalım. Koşula göre dört vektör verilmiştir ve görebileceğiniz gibi bunların bazı temellerde koordinatları zaten vardır. Bu temelin ne olduğu bizi ilgilendirmiyor. Ve şu şey ilgi çekicidir: Üç vektör pekala yeni bir temel oluşturabilir. Ve ilk aşama, Örnek 6'nın çözümüyle tamamen örtüşmektedir; vektörlerin gerçekten doğrusal olarak bağımsız olup olmadığının kontrol edilmesi gerekmektedir:

Vektör koordinatlarından oluşan determinantı hesaplayalım:

Bu, vektörlerin doğrusal olarak bağımsız olduğu ve üç boyutlu uzayın temelini oluşturduğu anlamına gelir.

! Önemli : vektör koordinatları mutlaka yaz sütunlara determinant, dizelerde değil. Aksi takdirde ilerideki çözüm algoritmasında karışıklık yaşanacaktır.

Vektörler, özellikleri ve bunlarla ilgili eylemler

Vektörler, vektörlerle eylemler, doğrusal vektör uzayı.

Vektörler sonlu sayıda gerçek sayıların sıralı bir koleksiyonudur.

Hareketler: 1.Bir vektörü bir sayıyla çarpmak: lambda*vektör x=(lamda*x 1, lambda*x 2 ... lambda*x n).(3.4, 0, 7)*3=(9, 12,0.21)

2. Vektörlerin toplamı (aynı vektör uzayına ait) vektör x + vektör y = (x 1 + y 1, x 2 + y 2, ... x n + y n,)

3. Vektör 0=(0,0…0)---n E n – n boyutlu (doğrusal uzay) vektör x + vektör 0 = vektör x

Teorem. n boyutlu bir doğrusal uzay olan n vektörden oluşan bir sistemin doğrusal bağımlı olabilmesi için, vektörlerden birinin diğerlerinin doğrusal birleşimi olması gerekli ve yeterlidir.

Teorem. Olayların n boyutlu doğrusal uzayının n+ 1. vektörlerinin herhangi bir kümesi. doğrusal bağımlı.

Vektörlerin toplanması, vektörlerin sayılarla çarpılması. Vektörlerin çıkarılması.

İki vektörün toplamı, başlangıcın vektörün sonu ile çakışması koşuluyla, vektörün başlangıcından vektörün sonuna doğru yönlendirilmiş bir vektördür. Vektörler temel birim vektörlerdeki açılımları ile veriliyorsa, vektörleri toplarken karşılık gelen koordinatları da eklenir.

Bunu Kartezyen koordinat sistemi örneğini kullanarak ele alalım. İzin vermek

Hadi bunu gösterelim

Şekil 3'ten açıkça görülüyor ki

Herhangi bir sonlu sayıda vektörün toplamı, çokgen kuralı kullanılarak bulunabilir (Şekil 4): sonlu sayıda vektörün toplamını oluşturmak için, sonraki her vektörün başlangıcını bir öncekinin sonuyla birleştirmek yeterlidir. ve ilk vektörün başlangıcını sonuncunun sonuna bağlayan bir vektör oluşturun.

Vektör toplama işleminin özellikleri:

Bu ifadelerde m, n sayılardır.

Vektörler arasındaki farka vektör denir. İkinci terim, vektörün yönüne zıt fakat uzunluğu ona eşit olan bir vektördür.

Böylece vektörleri çıkarma işleminin yerini toplama işlemi alır

Başlangıcı orijinde ve sonu A noktasında (x1, y1, z1) olan bir vektöre A noktasının yarıçap vektörü denir ve basitçe gösterilir. Koordinatları A noktasının koordinatlarıyla çakıştığı için birim vektörlerdeki açılımı şu şekildedir:

A(x1, y1, z1) noktasında başlayıp B(x2, y2, z2) noktasında biten bir vektör şu şekilde yazılabilir:

burada r2, B noktasının yarıçap vektörüdür; r 1 - A noktasının yarıçap vektörü.

Bu nedenle, vektörün birim vektörlerdeki açılımı şu şekildedir:

Uzunluğu A ve B noktaları arasındaki mesafeye eşittir

ÇARPMA İŞLEMİ

Yani bir düzlem problemi durumunda, bir vektörün a = (ax; ay) ile b sayısının çarpımı formülle bulunur

a b = (ax b; ay b)

Örnek 1. a = (1; 2) vektörünün 3'e çarpımını bulun.

3 bir = (3 1; 3 2) = (3; 6)

Yani uzaysal bir problem durumunda a = (ax; ay; az) vektörünün b sayısıyla çarpımı formülle bulunur.

a b = (ax b; ay b; az b)

Örnek 1. a = (1; 2; -5) vektörünün 2'ye çarpımını bulun.

2 a = (2 1; 2 2; 2 (-5)) = (2; 4; -10)

Vektörlerin nokta çarpımı ve ve vektörleri arasındaki açı nerede; eğer öyleyse, o zaman

Skaler çarpımın tanımından şu sonuç çıkar:

örneğin vektörün vektör yönüne izdüşümünün büyüklüğü buradadır.

Skaler kare vektör:

Nokta çarpımın özellikleri:

Koordinatlarda nokta çarpımı

Eğer O

Vektörler arasındaki açı

Vektörler arasındaki açı - bu vektörlerin yönleri arasındaki açı (en küçük açı).

Çapraz çarpım (İki vektörün çapraz çarpımı.) - bu, üç boyutlu Öklid uzayındaki vektörler üzerinde "vektör çarpımı" ikili işleminin sonucu olan, iki faktörden oluşturulmuş bir düzleme dik bir sözde vektördür. Çarpım ne değişmeli ne de birleşmeli (anti-değişmeli) ve vektörlerin nokta çarpımından farklıdır. Birçok mühendislik ve fizik probleminde, mevcut iki vektöre dik bir vektör oluşturabilmeniz gerekir; vektör çarpımı bu fırsatı sağlar. Çapraz çarpım, vektörlerin dikliğini "ölçmek" için kullanışlıdır - iki vektörün çapraz çarpımının uzunluğu, bunlar dikse uzunluklarının çarpımına eşittir ve vektörler paralel veya antiparalelse sıfıra düşer.

Çapraz çarpım yalnızca üç boyutlu ve yedi boyutlu uzaylarda tanımlanır. Bir vektör çarpımının sonucu, tıpkı bir skaler çarpım gibi, Öklid uzayının metriğine bağlıdır.

Üç boyutlu dikdörtgen koordinat sistemindeki koordinatlardan skaler çarpım vektörlerini hesaplama formülünün aksine, çapraz çarpım formülü dikdörtgen koordinat sisteminin yönüne veya başka bir deyişle "kiralliğine" bağlıdır.

Vektörlerin doğrusallığı.

Sıfır olmayan (0'a eşit olmayan) iki vektör, paralel çizgiler üzerinde veya aynı çizgide yer alıyorsa eşdoğrusal olarak adlandırılır. Kabul edilebilir ancak tavsiye edilmeyen bir eşanlamlı "paralel" vektörlerdir. Doğrusal vektörler aynı şekilde yönlendirilmiş ("eş-yönlü") veya zıt yönlü olabilir (ikinci durumda bunlara bazen "antikoldoğrusal" veya "antiparalel" denir).

Vektörlerin karışık çarpımı( a, b, c)- a vektörünün skaler çarpımı ile b ve c vektörlerinin vektör çarpımı:

(a,b,c)=a ⋅(b ×c)

bazen üçlü denir skaler çarpım vektörler, büyük olasılıkla sonucun bir skaler (daha kesin olarak bir sözde skaler) olması nedeniyle.

Geometrik anlam: Karışık çarpımın modülü sayısal olarak vektörlerin oluşturduğu paralelyüzün hacmine eşittir (ABC) .

Özellikler

Karışık parça tüm argümanlarına göre çarpık simetrik: yani. e. herhangi iki faktörün yeniden düzenlenmesi çarpımın işaretini değiştirir. Sağdaki karışık ürünün Kartezyen sistem koordinatlar (ortonormal temelde), vektörlerden oluşan bir matrisin determinantına eşittir ve:

Sol Kartezyen koordinat sistemindeki (ortonormal temelde) karışık çarpım, vektörlerden oluşan matrisin determinantına eşittir ve eksi işaretiyle alınır:

Özellikle,

Herhangi iki vektör paralelse, herhangi bir üçüncü vektörle sıfıra eşit bir karma çarpım oluştururlar.

Üç vektör doğrusal olarak bağımlıysa (yani aynı düzlemde yer alıyorsa), bunların karışık çarpımı sıfıra eşittir.

Geometrik anlam - Karışık ürün, mutlak değer olarak vektörlerin oluşturduğu paralel borunun (şekle bakınız) hacmine eşittir ve; işaret, bu vektör üçlüsünün sağ el veya solak olmasına bağlıdır.

Vektörlerin eş düzlemliliği.

Üç vektör (veya daha büyük sayı) ortak bir kökene indirgenerek aynı düzlemde yer alıyorlarsa eş düzlemli olarak adlandırılırlar.

Eş düzlemliliğin özellikleri

Üç vektörden en az biri sıfır ise, bu durumda üç vektör de aynı düzlemde kabul edilir.

Bir çift doğrusal vektör içeren üçlü bir vektör aynı düzlemlidir.

Eş düzlemli vektörlerin karışık çarpımı. Bu, üç vektörün eş düzlemliliği için bir kriterdir.

Eş düzlemli vektörler doğrusal olarak bağımlıdır. Bu aynı zamanda eş düzlemlilik için de bir kriterdir.

3 boyutlu uzayda aynı düzlemde olmayan 3 vektör bir temel oluşturur

Doğrusal bağımlı ve doğrusal bağımsız vektörler.

Doğrusal bağımlı ve bağımsız vektör sistemleri.Tanım. Vektör sistemi denir doğrusal bağımlı, eğer bu vektörlerin sıfır vektörüne eşit en az bir önemsiz olmayan doğrusal kombinasyonu varsa. Aksi takdirde, yani Verilen vektörlerin yalnızca önemsiz bir doğrusal kombinasyonu boş vektöre eşitse, vektörlere denir. Doğrusal bağımsız.

Teorem (doğrusal bağımlılık kriteri). Doğrusal uzaydaki bir vektörler sisteminin doğrusal bağımlı olabilmesi için bu vektörlerden en az birinin diğerlerinin doğrusal birleşimi olması gerekli ve yeterlidir.

1) Vektörler arasında en az bir sıfır vektör varsa, o zaman tüm vektör sistemi doğrusal olarak bağımlıdır.

Aslında, örneğin , varsayalım ki, önemsiz olmayan bir doğrusal birleşimimiz var.▲

2) Vektörlerden bazıları doğrusal bağımlı bir sistem oluşturuyorsa, sistemin tamamı doğrusal bağımlıdır.

Aslında, vektörlerin doğrusal olarak bağımlı olmasına izin verin. Bu, sıfır vektörüne eşit önemsiz olmayan bir doğrusal kombinasyonun olduğu anlamına gelir. Ama sonra varsayarsak Ayrıca sıfır vektörüne eşit önemsiz bir doğrusal kombinasyon da elde ederiz.

2. Temel ve boyut. Tanım. Doğrusal bağımsız vektörler sistemi vektör uzayı denir temel Bu uzayın herhangi bir vektörü bu sistemin vektörlerinin doğrusal bir kombinasyonu olarak temsil edilebiliyorsa, yani her vektör için gerçek sayılar vardır eşitliği sağlayacak şekildedir. Bu eşitliğe denir. vektör ayrışması esasa ve sayılara göre arandı vektörün tabana göre koordinatları(veya temelde) .

Teorem (tabana göre genişlemenin benzersizliği üzerine). Uzaydaki her vektör bir tabana genişletilebilir tek şekilde, yani tabandaki her vektörün koordinatları açık bir şekilde belirlenir.