Умножение сотых в столбик. Умножение натуральных чисел столбиком: примеры, решения

Если нам по ходу решения задачи требуется перемножить натуральные числа, удобно использовать для этого готовый способ, который называется "умножение в столбик" (или "умножение столбиком"). Это очень удобно, поскольку с его помощью можно свести умножение многозначных чисел к последовательному перемножению однозначных.

Основы умножения столбиком

Для ведения вычисления в столбик нам будет нужна таблица умножения. Важно помнить ее наизусть, чтобы считать быстро и эффективно.

Также потребуется вспомнить, какой результат мы получим при умножении натурального числа на нуль. Это часто встречается в примерах. Нам потребуется свойство умножения, которое в буквенном виде записывается как a · 0 = 0 (a – любое натуральное число).

Чтобы лучше понять, как умножать столбиком, рекомендуем вам повторить аналогичный метод сложения. Один из этапов подсчетов будет представлять собой именно сложение промежуточных результатов, и знание этого метода при складывании чисел нам пригодится.

Также важно, чтобы вы умели сравнивать натуральные числа и помнили, что такое разряд.

Как всегда, начнем с того, как правильно записать исходные числа. Нам нужно взять два множителя и записать их один под другим так, чтобы все цифры, отличные от нуля, были расположены друг под другом. Проведем под ними горизонтальную линию, отделяющую ответ, и добавим знак умножения с левой стороны.

Пример 1

Например, чтобы вычислить и 71 , 550 · 45 002 и 534 000 · 4 300 , запишем такие столбики:

Далее нам нужно разобраться с процессом умножения. Для начала посмотрим, как правильно умножать многозначное натуральное число на однозначное, а потом посмотрим, как перемножать между собой многозначные числа.

Если нам для решения задачи требуется выполнить умножение двух натуральных чисел, одно из которых однозначное, а второе многозначное, то мы можем использовать способ столбика. Для этого выполняем последовательность шагов, которую будем объяснять сразу на примере. Сначала возьмем задачу, в которой многозначное число имеет в конце цифру, отличную от нуля.

Пример 2

Условие: вычислить 45 027 · 3 .

Решение

Запишем множители так, как это предполагает метод умножения столбиком. Поместим однозначный множитель под последним знаком многозначного. Мы получили такую запись:

Далее нам надо выполнить последовательное перемножение разрядов многозначного числа на указанный множитель. Если у нас получается число, которое меньше десяти, мы сразу вносим его в поле ответа под горизонтальной чертой, строго под вычисляемым разрядом. Если же результат составил 10 и больше, то указываем под нужным разрядом только значение единиц из полученного числа, а десятки запоминаем и добавляем на следующем шаге к более старшему разряду.

На конкретных числах процесс будет выглядеть так:

1. Умножаем 7 на 3 (семерку мы взяли из разряда единиц первого многозначного множителя): 7 · 3 = 21 . Мы получили число больше десяти, значит, записываем с правого края число 1 (значение единичного разряда числа 21), а двойку запоминаем. Наша запись принимает вид:

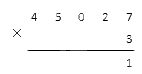
2. После этого мы перемножаем значения десятков первого множителя на второй и прибавляем к результату двойку, оставшуюся от предыдущего этапа. Если после этого получается меньше 10 , то вносим значения под соответствующий разряд, если больше – вносим значение единицы и переносим десятки дальше. В нашем примере нужно умножить 2 · 3 , это будет 6 . Добавляем оставшиеся с прошлого умножения десятки (от числа 21 , как мы помним): 6 + 2 = 8 . Восьмерка меньше десятки, значит, в следующий разряд переносить ничего не надо. Записываем 8 на нужное место и получаем:

3. Дальше действуем аналогично. Теперь нам надо умножить значения разряда сотен в первом многозначном множителе на исходный однозначный. Порядок действий тот же: если запоминали число на предыдущем этапе, плюсуем его к результату, сравниваем с десяткой и записываем в правильное место.

Здесь нужно умножить 3 на 0 . Согласно правилам умножения, результат будет равен 0 . Прибавлять ничего не будем, так как на предыдущем этапе число было меньше 10 . Получившийся нуль также меньше десятки, поэтому пишем его на место под горизонтальную черту:

4. Переходим к следующему разряду – умножаем тысячи. Продолжаем подсчеты по алгоритму до тех пора, пока не кончатся цифры в многозначном множителе.

Осталось умножить 5 · 3 и получить 15 . Результат больше 10 , пишем пятерку и запоминаем десяток:

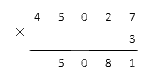
Нам осталось только перемножить 4 · 3 , это будет 12 . Добавляем к результату единицу, взятую из предыдущего подсчета. 13 больше 10 , пишем 3 на нужное место и сохраняем единицу.

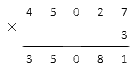
У нас больше не осталось разрядов, которые надо перемножить, однако единица в запасе все еще есть. Мы просто запишем ее под горизонтальную черту с левой стороны от всех уже имеющихся там цифр:

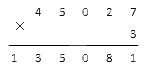
Процесс подсчета с помощью столбика на этом завершен. Мы получили шестизначное число, которое и является верным решением нашей задачи.

Ответ: 45 027 · 3 = 135 081 .

Чтобы было более понятно, мы представили алгоритм умножения многозначного натурального числа на однозначное в виде схемы. Здесь верно отражена самая суть процесса подсчета, однако не учтены некоторые нюансы:

Как быть, если в условии задачи стоит многозначное число, которое заканчивается нулем (или несколькими нулями подряд)? Рассмотрим на примере пошагово. Чтобы было проще, позаимствуем цифры из предыдущей задачи и просто допишем к исходному многозначному множителю пару нулей.

Решение

Cначала запишем числа нужным способом.

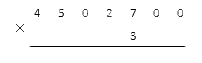
После этого проводим подсчеты, не обращая внимания на нули справа. Возьмем результаты из предыдущей задачи, чтобы не считать еще раз:

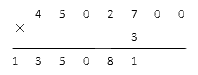
Финальный шаг решения – переписать имеющиеся в многозначном числе нули под горизонтальную черту в область результата. У нас нужно внести 2 дополнительных нуля:

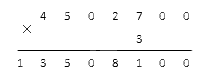
Это число и будет ответом нашей задачи. На этом умножение столбиком завершено.

Ответ: 4 502 700 · 3 = 13 508 100 .

Этот способ вполне подходит и для тех случаев, когда оба множителя представляют собой многозначные натуральные числа. Разберем процесс сразу на примере, как и раньше. Сначала возьмем числа без нулей в конце, а потом рассмотрим и записи с нулями.

Пример 4

Условие: вычислить, сколько будет 207 · 8 063 .

Решение

Начнем, как всегда, с правильной записи множителей. Более удобным является способ записи, при котором множитель с большим количеством знаков стоит сверху. Так что запишем сначала 8 063 , а под ним 207 . Если число знаков в множителях совпадает, то порядок записи не имеет значения. В нашей задаче нам надо разместить цифры первого множителя под цифрами второго справа налево:

Начинаем последовательно перемножать значения разрядов. При этом у нас будут получаться результаты, которые называются неполными произведениями.

1. Первый шаг состоит в том, что нам надо перемножить между собой значения единиц в первом и втором множителе. В нашем случае это 3 и 7 . Все делаем так же, как мы уже объясняли в предыдущем пункте (если нужно, прочитайте его еще раз). В итоге у нас получится первое неполное произведение, которое является промежуточным результатом:

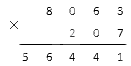
2. Второй шаг заключается в перемножении значений десятков. Умножаем столбиком первый множитель на значение разряда десятков второго множителя (при условии, что он не равен 0). Записываем результат под чертой под разрядом десятков. Если же во втором множителе на месте десятков стоит 0 , то сразу переходим к следующему этапу.

3. Последующие шаги выполняем аналогично, перемножая по очереди значения нужных разрядов (если они не равны 0). Вносим результаты под черту.

Итак, нам надо умножить 8 063 на значения сотен в 207 (т.е. на два). Мы получили второе неполное произведение, запишем его так:

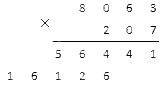
У нас получились все нужные нам неполные произведения. Их количество равно числу разрядов во втором множителе (кроме 0). Последнее, что нам осталось сделать, – это сложить два произведения в столбик, используя ту же запись. Мы никуда не переписываем цифры: они остаются с тем же сдвигом влево. Подчеркнем их дополнительной горизонтальной чертой и поставим слева плюс. Складываем согласно уже изученным правилам сложения в столбик (запоминаем десятки, если число получилось больше 10 , и прибавляем их на следующем этапе). В нашей задаче получится:

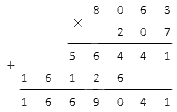
Получившееся под чертой семизначное число – это и есть нужный нам результат умножения исходных натуральных чисел.

Ответ: 8 063 · 207 = 1 669 041 .

Процесс умножения двух многозначных чисел столбиков также можно представить в виде наглядной схемы:

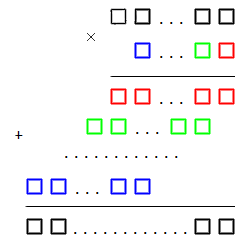
Чтобы лучше закрепить материал, приведем решение еще одного примера.

Пример 5

Условие: умножьте 297 на 321 .

Решение

Начинаем с правильной записи множителей. Количество знаков в них одинаковое, так что порядок записи особого значения не имеет:

1. Первый этап – умножаем 297 на 1 , которая стоит в разряде единиц второго множителя.

2. Потом умножаем таким же образом первый множитель на 2 , что стоит в десятках второго множителя. Получаем второе неполное произведение.

Если вы уже запамятовали, как умножать цифры в столбик, то прочитайте статью. Тут вы найдете всю информацию об этом математическом действии.

Даже некоторые взрослые не освоили в школе, как можно умножать числа в столбик. А ведь это умение может и пригодиться в жизни, если не будет под рукой калькулятора или мобильного телефона.

Тем более, что это совсем не трудно, если вы знаете таблицу умножения и поняли, как правильно располагать цифры при данном процессе. Умножение в столбик всегда начинают изучать с умножения многозначного числа на однозначное, чтобы понять правила данного действия. Далее подробней.

Правила и алгоритм умножения в столбик

Математические занятия многим детям даются не с первого раза. Это непростая наука, требующая особого внимания, понимания. И ученикам в начальных классах в обязательном порядке необходима помощь мамы и папы в решении сложных примеров, задач. В частности нельзя все оставлять на самотеке, если ваше чадо не поняло, что такое умножение, деление чисел и т.п. Надо помочь разобраться в теме и выучить таблицу умножения, чтобы потом не получать плохие оценки, и не расстраиваться.

Освоить умножение в столбик будет легко, если:

• Школьник отлично знает таблицу умножения. Не путается в значениях произведения.
• Уяснил, в какой последовательности следует перемножать цифры многозначного числа.
• Ребенок понял, где их правильно писать. И умеет производить сложение многочленов в столбик.

Нужно знать, правило, что от перемены мест множителей произведение не меняется. Точнее, если умножить 56 ⋅ 2 = 112 и 2 ⋅ 56 = 112 — произведение будет 112.

ВАЖНО : Когда перемножают цифры в столбик. Под низом пишут то число, которое имеет меньше цифр в своем составе.

Как правильно умножать в столбик трехзначные числа на однозначные, двузначные, трехзначные

Любое умножение — это сложение одинаковых цифр необходимое количество раз. Точнее 725 ⋅ 2 = 725 + 725 = 1450. Но такой пример можно сделать устно, если второе число — 2,3,4. А если это — 8, то перемножать уже лучше в столбик. Для этого:

1. Вверху нужно написать цифру 725 , а внизу под цифрой — 5 написать число — 8 .
2. Теперь нужно поочередно, начиная с 5 , все значения трёхзначного числа перемножить на 8 .
3. Точнее: 5 ⋅ 8 = 40 (ноль пишем ниже под восьмеркой и пятеркой, а — 4 запоминаем ).
4. Далее умножаем: 2 ⋅ 8 = 16 (к 16 прибавляем — 4 = 20, опять 0 пишем, только уже под двойкой, а — 2 запоминаем ).
5. Остается умножить: 7 ⋅ 8 = 56 (к 56 прибавляем — 2 = 58, восьмерку пишем под семеркой, а пять впереди ).
6. В результате такого умножения (725 ⋅ 8 ) получатся — 5800 . И этот расчет получен вручную, без каких-либо машинок, калькуляторов.

Умножение в столбик — трехзначное на трехзначное

Умножить многочлен на многочлен несколько сложнее. Однако, если вы уже в первом примере уяснили, как происходит процесс, то вам не составит труда перемножить и трехзначные числа, а потом сложить в столбик, получившиеся значения.

Рассмотрим в подробностях, как умножить 125 на 32

1. Вверху на листке напишите трехзначное число 125, под ним 32, причем расположите его следующим образом: тройку под двойкой первого числа , а двойку второго под пятеркой первого числа — это очень важно.
2. Начните перемножать с конца. То есть: перемножьте все цифры трехзначного числа (125) вначале на двойку .
3. У вас получится 250 , ноль напишите под двойкой , остальные цифры впереди.
4. Далее перемножайте 125 на три . И располагайте на листике значение произведения (375 ), начиная с цифры — 3 .
5. Теперь остается сложить 250 и 375(0) , получится 250 + 3750 = 4000.

ВАЖНО : Как перемножить трёхзначные числа наглядно можно увидеть на рисунке выше. Цифры перемножаются в строгой последовательности, начиная с конца, а потом все получившиеся значения складываются.

Как правильно умножать в столбик числа с нулями?

Уже из математики начальных классов любой ученик знает, что, если умножить любое число на ноль, то произведение будет тоже 0. Именно поэтому, когда производится умножение в столбик, то на цифру ноль умножение не производится, его выносят за рамки, а в произведении приписывают ноль или несколько нулей — смотрите на изображении ниже.

Как объяснить ребенку умножение столбиком?

• Если вы дома решили провести урок по математике, изучить, как производить умножение в столбик, то превратите ваше занятие в игру.
• Постепенно, терпеливо объясняя, как это делается. Отвечайте на все вопросы школьника, чтобы ему было понятно, что и за чем делать.
• Дайте вначале для примеров несложные примеры, а потом уже выбирайте задания потруднее.

ВАЖНО : Уделяйте больше времени своим детям, не игнорируйте их просьбы о помощи. В школе учитель соблюдает программные требования. На закрепление материала дается не много времени. Поэтому не все школьники успевают освоить программу, тем более в таком сложном деле, как умножение, деление в столбик.

Видео: Примеры умножения многозначных чисел в столбик с пояснениями

В школе эти действия изучаются от простого к сложному. Поэтому непременно полагается хорошо усвоить алгоритм выполнения названных операций на простых примерах. Чтобы потом не возникло трудностей с делением десятичных дробей в столбик. Ведь это самый сложный вариант подобных заданий.

Этот предмет требует последовательного изучения. Пробелы в знаниях здесь недопустимы. Такой принцип должен усвоить каждый ученик уже в первом классе. Поэтому при пропуске нескольких уроков подряд материал придется освоить самостоятельно. Иначе позже возникнут проблемы не только с математикой, но и другими предметами, связанными с ней.

Второе обязательное условие успешного изучения математики — переходить к примерам на деление в столбик только после того, как освоены сложение, вычитание и умножение.

Ребенку будет трудно делить, если он не выучил таблицу умножения. Кстати, ее лучше учить по таблице Пифагора. Там нет ничего лишнего, да и усваивается умножение в таком случае проще.

Как умножаются в столбик натуральные числа?

Если возникает затруднение в решении примеров в столбик на деление и умножение, то начинать устранять проблему полагается с умножения. Поскольку деление является обратной операцией умножению:

1. До того как перемножать два числа, на них нужно внимательно посмотреть. Выбрать то, в котором больше разрядов (длиннее), записать его первым. Под ним разместить второе. Причем цифры соответствующего разряда должны оказаться под тем же разрядом. То есть самая правая цифра первого числа должна быть над самой правой второго.
2. Умножьте крайнюю правую цифру нижнего числа на каждую цифру верхнего, начиная справа. Запишите ответ под чертой так, чтобы его последняя цифра была под той на которую умножали.
3. То же повторите с другой цифой нижнего числа. Но результат от умножения при этом нужно сместить на одну цифру влево. При этом его последняя цифра окажется под той, на которую умножали.

Продолжать такое умножение в столбик до тех пор, пока не закончатся цифры во втором множителе. Теперь их нужно сложить. Это и будет искомый ответ.

Алгоритм умножения в столбик десятичных дробей

Сначала полагается представить, что даны не десятичные дроби, а натуральные. То есть убрать из них запятые и далее действовать так, как описано в предыдущем случае.

Отличие начинается, когда записывается ответ. В этот момент необходимо сосчитать все цифры, которые стоят после запятых в обеих дробях. Именно столько их нужно отсчитать от конца ответа и там поставить запятую.

Удобно проиллюстрировать этот алгоритм на примере: 0,25 х 0,33:

С чего начать обучение делению?

До того как решать примеры на деление в столбик, полагается запомнить названия чисел, которые стоят в примере на деление. Первое из них (то, которое делится) — делимое. Второе (на него делят) — делитель. Ответ — частное.

После этого на простом бытовом примере объясним суть этой математической операции. Например, если взять 10 конфет, то поделить их поровну между мамой и папой легко. А как быть, если нужно раздать их родителям и брату?

После этого можно знакомиться с правилами деления и осваивать их на конкретных примерах. Сначала простых, а потом переходить ко все более сложным.

Алгоритм деления чисел в столбик

Вначале представим порядок действий для натуральных чисел, делящихся на однозначное число. Они будут основой и для многозначных делителей или десятичных дробей. Только тогда полагается внести небольшие изменения, но об этом позже:

• До того как делать деление в столбик, нужно выяснить, где делимое и делитель.
• Записать делимое. Справа от него - делитель.
• Прочертить слева и снизу около последнего уголок.
• Определить неполное делимое, то есть число, которое будет минимальным для деления. Обычно оно состоит из одной цифры, максимум из двух.
• Подобрать число, которое будет первым записано в ответ. Оно должно быть таким, сколько раз делитель помещается в делимом.
• Записать результат от умножения этого числа на делитель.
• Написать его под неполным делимом. Выполнить вычитание.
• Снести к остатку первую цифру после той части, которая уже разделена.
• Снова подобрать число для ответа.
• Повторить умножение и вычитание. Если остаток равен нулю и делимое закончилось, то пример сделан. В противном случае повторить действия: снести цифру, подобрать число, умножить, вычесть.

Как решать деление в столбик, если в делителе больше одной цифры?

Сам алгоритм полностью совпадает с тем, что был описан выше. Отличием будет количество цифр в неполном делимом. Их теперь минимум должно быть две, но если они оказываются меньше делителя, то работать полагается с первыми тремя цифрами.

Существует еще один нюанс в таком делении. Дело в том, что остаток и снесенная к нему цифра иногда не делятся на делитель. Тогда полагается приписать еще одну цифру по порядку. Но при этом в ответ необходимо поставить ноль. Если осуществляется деление трехзначных чисел в столбик, то может потребоваться снести больше двух цифр. Тогда вводится правило: нолей в ответе должно быть на один меньше, чем количество снесенных цифр.

Рассмотреть такое деление можно на примере - 12082: 863.

• Неполным делимым в нем оказывается число 1208. В него число 863 помещается только один раз. Поэтому в ответ полагается поставить 1, а под 1208 записать 863.
• После вычитания получается остаток 345.
• К нему нужно снести цифру 2.
• В числе 3452 четыре раза умещается 863.
• Четверку необходимо записать в ответ. Причем при умножении на 4 получается именно это число.
• Остаток после вычитания равен нулю. То есть деление закончено.

Ответом в примере будет число 14.

Как быть, если делимое заканчивается на ноль?

Или несколько нолей? В этом случае нулевой остаток получается, а в делимом еще стоят нули. Отчаиваться не стоит, все проще, чем может показаться. Достаточно просто приписать к ответу все нули, которые остались не разделенными.

Например, нужно поделить 400 на 5. Неполное делимое 40. В него 8 раз помещается пятерка. Значит, в ответ полагается записать 8. При вычитании остатка не остается. То есть деление закончено, но в делимом остался ноль. Его придется приписать к ответу. Таким образом, при делении 400 на 5 получается 80.

Что делать, если разделить нужно десятичную дробь?

Опять же, это число похоже на натуральное, если бы не запятая, отделяющая целую часть от дробной. Это наводит на мысль о том, что деление десятичных дробей в столбик подобно тому, которое было описано выше.

Единственным отличием будет пункт с запятой. Ее полагается поставить в ответ сразу, как только снесена первая цифра из дробной части. По-другому это можно сказать так: закончилось деление целой части — поставь запятую и продолжай решение дальше.

Во время решения примеров на деление в столбик с десятичными дробями нужно помнить, что в части после запятой можно приписать любое количество нолей. Иногда это нужно для того, чтобы доделить числа до конца.

Деление двух десятичных дробей

Оно может показаться сложным. Но только вначале. Ведь то, как выполнить деление в столбик дробей на натуральное число, уже понятно. Значит, нужно свести этот пример к уже привычному виду.

Сделать это легко. Нужно умножить обе дроби на 10, 100, 1 000 или 10 000, а может быть, на миллион, если этого требует задача. Множитель полагается выбирать исходя из того, сколько нолей стоит в десятичной части делителя. То есть в результате получится, что делить придется дробь на натуральное число.

Причем это будет в худшем случае. Ведь может получиться так, что делимое от этой операции станет целым числом. Тогда решение примера с делением в столбик дробей сведется к самому простому варианту: операции с натуральными числами.

В качестве примера: 28,4 делим на 3,2:

• Сначала их необходимо умножить на 10, поскольку во втором числе после запятой стоит только одна цифра. Умножение даст 284 и 32.
• Их полагается разделить. Причем сразу все число 284 на 32.
• Первым подобранным числом для ответа является 8. От его умножения получается 256. Остатком будет 28.
• Деление целой части закончилось, и в ответ полагается поставить запятую.
• Снести к остатку 0.
• Снова взять по 8.
• Остаток: 24. К нему приписать еще один 0.
• Теперь брать нужно 7.
• Результат умножения - 224, остаток - 16.
• Снести еще один 0. Взять по 5 и получится как раз 160. Остаток — 0.

Деление закончено. Результат примера 28,4:3,2 равен 8,875.

Что делать, если делитель равен 10, 100, 0,1, или 0,01?

Так же как и с умножением, деление в столбик здесь не понадобится. Достаточно просто переносить запятую в нужную сторону на определенное количество цифр. Причем по этому принципу можно решать примеры как с целыми числами, так и с десятичными дробями.

Итак, если нужно делить на 10, 100 или 1 000, то запятая переносится влево на такое количество цифр, сколько нулей в делителе. То есть, когда число делится на 100, запятая должна сместиться влево на две цифры. Если делимое — натуральное число, то подразумевается, что запятая стоит в его конце.

Это действие дает такой же результат, как если бы число было необходимо умножить на 0,1, 0,01 или 0,001. В этих примерах запятая тоже переносится влево на количество цифр, равное длине дробной части.

При делении на 0,1 (и т. д.) или умножении на 10 (и т. д.) запятая должна переместиться вправо на одну цифру (или две, три, в зависимости от количества нулей или длины дробной части).

Стоит отметить, что количества цифр, данных в делимом, может быть недостаточным. Тогда слева (в целой части) или справа (после запятой) можно приписать недостающие нули.

Деление периодических дробей

В этом случае не удастся получить точный ответ при делении в столбик. Как решать пример, если встретилась дробь с периодом? Здесь полагается переходить к обыкновенным дробям. А потом выполнять их деление по изученным ранее правилам.

Например разделить нужно 0,(3) на 0,6. Первая дробь — периодическая. Она преобразуется в дробь 3/9, которая после сокращения даст 1/3. Вторая дробь — конечная десятичная. Ее записать обыкновенной еще проще: 6/10, что равно 3/5. Правило деления обыкновенных дробей предписывает заменять деление умножением и делитель — обратным числом. То есть пример сводится к умножению 1/3 на 5/3. Ответом будет 5/9.

Если в примере разные дроби...

Тогда возможны несколько вариантов решения. Во-первых, обыкновенную дробь можно попытаться перевести в десятичную. Потом делить уже две десятичные по указанному выше алгоритму.

Во-вторых, каждая конечная десятичная дробь может быть записана в виде обыкновенной. Только это не всегда удобно. Чаще всего такие дроби оказываются огромными. Да и ответы получаются громоздкими. Поэтому первый подход считается более предпочтительным.

Многие родители, чьи дети окончили первый класс, задают себе вопрос: как же помочь ребенку быстро выучить таблицу умножения. На лето детям задают выучить эту таблицу, и не всегда ребенок проявляет желание летом заниматься зубрежкой. Тем более, что если просто механически зазубрить и не закрепить результат, то можно впоследствии и забыть некоторые примеры.

В этой статье читайте способы, как быстро выучить таблицу умножения. Конечно, за 5 минут этого сделать не получиться, но за несколько занятий вполне можно достичь хорошего результата.

Также читайте статью,

В самом начале нужно объяснить ребенку, что такое умножение (если он еще не знает). Покажите смысл умножения на простом примере. К примеру, 3*2 — это значит, что цифру 3 нужно 2 раза сложить. То есть 3*2=3+3. А 3*3 — значит, цифру 3 нужно сложить 3 раза. То есть 3*3=3+3+3. И так далее. Понимая суть таблицы умножения, ребенку легче будет ее выучить.

Детям будет легче воспринимать таблицу умножения не в виде столбиков, а в виде пифагоровой таблицы. Она выглядит вот так:

Объясните, что числа на пересечении столбика и строчки — это результат умножения. Изучать такую таблицу ребенку намного интереснее, ведь тут можно найти определенные закономерности. И, когда посмотришь внимательно на эту таблицу, видно, что числа, выделенные одним цветом, повторяются.

Из этого ребенок даже сам сможет сделать вывод (а это уже будет развитие мозга), что при умножении при перемене множителей местами произведение не меняется. То есть он поймет, что 6*4=24 и 4*6=24 и так далее. То есть учить надо не всю таблицу, а половину! Поверьте, увидев первый раз всю таблицу (ого, сколько надо выучить!), ребенку станет грустно. Но, поняв, что учить надо половину, он заметно повеселеет.

Таблицу Пифагора распечатайте и повесьте на видном месте. Каждый раз, глядя на нее, ребенок будет запоминать и повторять какие-то примеры. Этот момент очень важен.

Начинать изучения таблицы нужно от простого к сложному: вначале выучите умножение на 2, 3, а потом на другие числа.

Для легкого запоминания таблицы используют различные инструменты: стихи, карточки, онлайн-тренажеры, небольшие секреты умножения.

Карточки — один из лучших способов быстро выучить таблицу умножения

Таблицу умножения нужно учить постепенно: в день можно брать для запоминания по одному столбику. Когда будет выучено умножение на какое-либо число, нужно закрепить результат с помощью карточек.

Карточки можете сделать сами, а можете распечатать уже готовые. Скачать карточки можете по ссылке ниже.

Скачать карточки для изучения таблицы умножения.

На одной стороне карточки пишутся умножаемые числа, на другой — ответ. Все карточки складываются ответом вниз. Ученик тянет поочередно карты из колоды, отвечая на заданный пример. Если ответ назван верный, карточка откладывается в сторону, если школьник ошибся — карточка возвращается в общую колоду.

Таким образом тренируется память, и таблица умножения быстрее учится. Ведь, играя, всегда интереснее учиться. В игре с карточками работает и зрительная память, и слуховая (нужно озвучить уравнение). А также учащийся хочет поскорее «расправиться» со всеми карточками.

Когда немного выучили умножение на 2, сыграли в карточки с умножением на 2. Выучили умножение на 3, сыграли в карточки с умножением на 2 и 3. И так далее.

Умножение на 1 и 10

Это самые легкие примеры. Тут даже заучивать ничего не надо, просто понять, как умножаются числа на 1 и на 10. Начните изучение таблицы с умножения на эти числа. Объясните ребенку, что при умножении на 1 получится то же умножаемое число. Умножить на один — означает взять какое-то число один раз. Тут не должно возникнуть сложностей.

Умножить на 10 — означает, что нужно сложить число 10 раз. И всегда получится число в 10 раз больше умножаемого. То есть для получения ответа нужно просто дописать ноль к умножаемому числу! Ребенок с легкостью сможет превратить единицы в десятки, прибавив ноль. Поиграйте с учеником в карточки, чтобы он лучше запомнил все ответы.

Умножение на 2

Умножение на 2 ребенок может выучить за 5 минут. Ведь в школе он уже научился складывать единицы. А умножение на 2 — не что иное, как сложение двух одинаковых чисел. Когда ребенок знает, что 2*2 = 2+2, а 5*2 = 5+5 и так далее, то этот столбик никогда не станет для него камнем преткновения.

Умножение на 4

После того, как выучили умножение на 2, переходите к умножению на 4. Этот столбик ребенку будет легче запомнить, чем умножение на 3. Чтобы легко выучить умножение на 4, распишите ребенку, что умножение на 4 — это умножение на 2, только два раза. То есть сначала умножаем на два, а потом полученный результат еще на 2.

Например, 5*4 = 5*2 *2 = 5+5 (как при умножении на 2 нужно сложить одинаковые числа, получаем 10) + 10 = 20.

Умножение на 3

Если с изучением этого столбика возникнут сложности, можно обратиться за помощью к стихам. Стихи можно взять готовые, а можно придумать самому. У детей хорошо развита ассоциативная память. Если ребенку показать наглядный пример умножения на каких либо предметах из его окружения, то он легче запомнит ответ, который у него будет ассоциироваться с каким-либо предметом.

Например, разложите карандаши в 3 кучки по 4 (или 5, 6, 7, 8, 9 — смотря какой пример ребенок забывает) штук. Придумайте задачку: у тебя есть 4 карандаша, у папы есть 4 карандаша и у мамы есть 4 карандаша. Сколько всего карандашей? Посчитайте карандаши и сделайте вывод, что 3*4 = 12. Иногда такая визуализация очень помогает запомнить «сложный» пример.

Умножение на 5

Помню, для меня этот столбик был самым легким для запоминания. Потому что каждое следующее произведение увеличивается на 5. Если умножать четное число на 5, в ответе получится тоже четное число, заканчивающееся на 0. Дети легко это запоминают: 5*2 = 10, 5*4 = 20, 5*6 = 30 и т.д. Если умножать нечетное число, то в ответе получим нечетное число, заканчивающееся на 5: 5*3 = 15, 5*5 = 25 и т. д.

Умножение на 9

Пишу после 5 сразу 9, потому что в умножении на 9 есть маленький секретик, который поможет быстро выучить этот столбик. Выучить умножение на 9 можно с помощью пальцев!

Для этого положите руки ладонями вверх, пальцы разогните. Мысленно пронумеруйте пальцы слева направо от 1 до 10. Загните тот палец, на какое число нужно умножить 9. Например, нужно 9*5. Загибаете 5 палец. Все пальцы слева (их 4 — это десятки), пальцы справа (их 5) — единицы. Соединяем десятки и единицы, получаем — 45.

Еще один пример. Сколько будет 9*7? Загибаем седьмой палец. Слева остается 6 пальцев, справа — 3. Соединяем, получаем — 63!

Чтобы лучше понять этот простой способ выучить умножение на 9 — посмотрите видео.

Еще один интересный факт об умножении на 9. Посмотрите на картинку ниже. Если записать столбиком умножение на 9 с 1 до 10, то можно заметить, что произведения будут иметь некую закономерность. Первые цифры будут от 0 до 9 сверху вниз, вторые цифры — от 0 до 9 снизу вверх.

Также, если внимательно посмотреть на получившийся столбик, можно заметить, что сумма чисел в произведении равна 9. К примеру, 18 — это 1+8=9, 27 — это 2+7=9, 36 — это 3+6=9 и так далее.

Второе интересное наблюдение такое: первая цифра ответа всегда на 1 меньше, чем число, на которое умножается 9. То есть 9×5 =4 5 — 4 на один меньше, чем 5; 9×9 =8 1 — 8 на один меньше, чем 9. Зная это, легко вспомнить, на какую цифру начинается ответ при умножении на 9. Если вторую цифру забыли, то ее легко можно посчитать, зная, что сумма чисел в ответе равна 9.

Например, сколько будет 9×6 ? Сразу понимаем, что ответ будет начинаться на цифру 5 (на один меньше, чем 6). Вторая цифра: 9-5=4 (потому что сумма чисел 4+5=9). Получается 54!

Умножение на 6,7,8

Когда вы с ребенком приступите к изучению умножения на эти числа, он уже будет знать умножение на 2, 3, 4, 5, 9. С самого начала Вы объяснили ему, что 5×6 — это то же самое, что 6×5. Значит, некоторые ответы он уже знает, их не нужно учить сначала.

Остальные уравнения нужно выучить. Используйте таблицу Пифагора и игру в карточки для лучшего запоминания.

Есть один способ, как посчитать ответ при умножении на 6, 7, 8 на пальцах. Но он более сложный, чем при умножении на 9, потребуется время для подсчета. Но, если какой-то пример никак не хочет запоминаться, попробуйте с ребенком посчитать на пальцах, возможно, ему так будет проще выучить эти самые сложные столбики.

Чтобы легче запомнить самые сложные примеры из таблицы умножения, порешайте с ребенком простые задачки с нужными числами, приведите пример из жизни. Все дети любят ходить в магазин с родителями. Придумайте ему задачку на эту тему. Например, ученик никак не может запомнить, сколько будет 7×8. Тогда смоделируйте ситуацию: у него День рождения. Он пригласил в гости 7 друзей. Каждого друга нужно угостить 8 конфетами. Сколько конфет он купит в магазине для друзей? Ответ 56 он запомнит намного быстрее, зная, что это количество угощений для друзей.

Запоминать таблицу умножения можно не только дома. Если Вы с ребенком на улице, то можно решать задачки, исходя из того, что вы видите. Например, мимо вас пробежало 4 собаки. Спросите ребенка, сколько всего у собак лап, ушей, хвостов?

Также дети очень любят играть на компьютере. Так пусть играют с пользой. Включите ученику онлайн-тренажер для запоминания таблицы умножения.

Занимайтесь изучением таблицы умножения, когда у ребенка хорошее настроение. Если он устал, начал капризничать, то лучше оставьте дальнейшее обучение на другой раз.

Используйте те методы, которые больше подходят Вашему ребенку, и все получится!

Желаю легкого и быстрого запоминания таблицы умножения!

Математический-Калькулятор-Онлайн v.1.0

Калькулятор выполняет следующие операции: сложение, вычитание, умножение, деление, работа с десятичными, извлечение корня, возведение в степень, вычисление процентов и др. операции.

Решение:

Как работать с математическим калькулятором

Клавиша	Обозначение	Пояснение
5	цифры 0-9	Арабские цифры. Ввод натуральных целых чисел, нуля. Для получения отрицательного целого числа необходимо нажать клавишу +/-
.	точка (запятая)	Разделитель для обозначения десятичной дроби. При отсутствии цифры перед точкой (запятой) калькулятор автоматически подставит ноль перед точкой. Например: .5 - будет записано 0.5
+	знак плюс	Сложение чисел (целые, десятичные дроби)
-	знак минус	Вычитание чисел (целые, десятичные дроби)
÷	знак деления	Деление чисел (целые, десятичные дроби)
х	знак умножения	Умножение чисел (целые, десятичные дроби)
√	корень	Извлечение корня из числа. При повторном нажатие на кнопку "корня" производится вычисление корня из результата. Например: корень из 16 = 4; корень из 4 = 2
x 2	возведение в квадрат	Возведение числа в квадрат. При повторном нажатие на кнопку "возведение в квадрат" производится возведение в квадрат результата Например: квадрат 2 = 4; квадрат 4 = 16
1 / x	дробь	Вывод в десятичные дроби. В числителе 1, в знаменателе вводимое число
%	процент	Получение процента от числа. Для работы необходимо ввести: число из которого будет высчитываться процент, знак (плюс, минус, делить, умножить), сколько процентов в численном виде, кнопка "%"
(	открытая скобка	Открытая скобка для задания приоритета вычисления. Обязательно наличие закрытой скобки. Пример: (2+3)*2=10
)	закрытая скобка	Закрытая скобка для задания приоритета вычисления. Обязательно наличие открытой скобки
±	плюс минус	Меняет знак на противоположный
=	равно	Выводит результат решения. Также над калькулятором в поле "Решение" выводится промежуточные вычисления и результат.
←	удаление символа	Удаляет последний символ
С	сброс	Кнопка сброса. Полностью сбрасывает калькулятор в положение "0"

Алгоритм работы онлайн-калькулятора на примерах

Сложение.

Сложение целых натуральных чисел { 5 + 7 = 12 }

Сложение целых натуральных и отрицательных чисел { 5 + (-2) = 3 }

Сложение десятичных дробных чисел { 0,3 + 5,2 = 5,5 }

Вычитание.

Вычитание целых натуральных чисел { 7 - 5 = 2 }

Вычитание целых натуральных и отрицательных чисел { 5 - (-2) = 7 }

Вычитание десятичных дробных чисел { 6,5 - 1,2 = 4,3 }

Умножение.

Произведение целых натуральных чисел { 3 * 7 = 21 }

Произведение целых натуральных и отрицательных чисел { 5 * (-3) = -15 }

Произведение десятичных дробных чисел { 0,5 * 0,6 = 0,3 }

Деление.

Деление целых натуральных чисел { 27 / 3 = 9 }

Деление целых натуральных и отрицательных чисел { 15 / (-3) = -5 }

Деление десятичных дробных чисел { 6,2 / 2 = 3,1 }

Извлечение корня из числа.

Извлечение корня из целого числа { корень(9) = 3 }

Извлечение корня из десятичных дробей { корень(2,5) = 1,58 }

Извлечение корня из суммы чисел { корень(56 + 25) = 9 }

Извлечение корня из разницы чисел { корень (32 – 7) = 5 }

Возведение числа в квадрат.

Возведение в квадрат целого числа { (3) 2 = 9 }

Возведение в квадрат десятичных дробей { (2,2) 2 = 4,84 }

Перевод в десятичные дроби.

Вычисление процентов от числа

Увеличить на 15% число 230 { 230 + 230 * 0,15 = 264,5 }

Уменьшить на 35% число 510 { 510 – 510 * 0,35 =331,5 }

18% от числа 140 это { 140 * 0,18 = 25,2 }