Главная / Натяжные потолки

Ускорение формула. Ускорение

Как изменяются показания спидометра в начале движения и при торможении автомобиля?
Какая физическая величина характеризует изменение скорости?

При движении тел их скорости обычно меняются либо по модулю, либо по направлению, либо жеодновременно как по модулю, так и по направлению.

Скорость шайбы, скользящей по льду, уменьшается с течением времени до полной остановки. Если взять в руки камень и разжать пальцы, то при падении камня его скорость постепенно нарастает. Скорость любой точки окружности точильного круга при неизменном числе оборотов в единицу времени меняется только по направлению, оставаясь постоянной по модулю (рис 1.26). Если бросить камень под углом к горизонту, то его скорость будет меняться и по модулю, и по направлению.

Изменение скорости тела может происходить как очень быстро (движение пули в канале ствола при выстреле из винтовки), так и сравнительно медленно (движение поезда при его отправлении).

Физическая величина, характеризующая быстроту изменения скорости, называется ускорением .

Рассмотрим случай криволинейного и неравномерного движения точки. В этом случае её скорость с течением времени изменяется как по модулю, так и по направлению. Пусть в некоторый момент времени t точка занимает положение М и имеет скорость (рис. 1.27). Спустя промежуток времени Δt точка займёт положение М 1 и будет иметь скорость 1 . Изменение скорости за время Δt 1 равно Δ 1 = 1 - . Вычитание вектора можно произвести путём прибавления к вектору 1 вектора (-):

Δ 1 = 1 - = 1 + (-).

Согласно правилу сложения векторов вектор изменения скорости Δ 1 направлен из начала вектора 1 в конец вектора (-), как это показано на рисунке 1.28.

Поделив вектор Δ 1 на промежуток времени Δt 1 получим вектор, направленный так же, как и вектор изменения скорости Δ 1 . Этот вектор называют средним ускорением точки за промежуток времени Δt 1 . Обозначив его через cр1 , запишем:

По аналогии с определением мгновенной скорости определим мгновенное ускорение . Для этого найдём теперь средние ускорения точки за всё меньшие и меньшие промежутки времени:

При уменьшении промежутка времени Δt вектор Δ уменьшается по модулю и меняется по направлению (рис. 1.29). Соответственно средние ускорения также меняются по модулю и направлению. Но при стремлении промежутка времени Δt к нулю отношение изменения скорости к изменению времени стремится к определённому вектору как к своему предельному значению. В механике эту величину называют ускорением точки в данный момент времени или просто ускорением и обозначают .

Ускорение точки - это предел отношения изменения скорости Δ к промежутку времени Δt, в течение которого это изменение произошло, при стремлении Δt к нулю.

Ускорение направлено так, как направлен вектор изменения скорости Δ при стремлении промежутка времени Δt к нулю. В отличие от направления скорости, направление вектора ускорения нельзя определить, зная траекторию точки и направление движения точки по траектории. В дальнейшем на простых примерах мы увидим, как можно определить направление ускорения точки при прямолинейном и криволинейном движениях.

В общем случае ускорение направлено под углом к вектору скорости (рис. 1.30). Полное ускорение характеризует изменение скорости и по модулю, и по направлению. Часто полное ускорение считается равным векторной сумме двух ускорений - касательного ( к) и центростремительного ( цс). Касательное ускорение к характеризует изменение скорости по модулю и направлено по касательной к траектории движения. Центростремительное ускорение цс характеризует изменение скорости по направлению и перпендикулярно касательной, т. е. направлено к центру кривизны траектории в данной точке. В дальнейшем мы рассмотрим два частных случая: точка движется по прямой и скорость изменяется только по модулю; точка движется равномерно по окружности и скорость изменяется только по направлению.

Единица ускорения.

Движение точки может происходить как с переменным, так и с постоянным ускорением. Если ускорение точки постоянно, то отношение изменения скорости к промежутку времени, за которое это изменение произошло, будет одним и тем же для любого интервала времени. Поэтому обозначив через Δt некоторый произвольный промежуток времени, а через Δ - изменение скорости за этот промежуток, можно записать:

Так как промежуток времени Δt - величина положительная, то из этой формулы следует, что если ускорение точки с течением времени не изменяется, то оно направлено так же, как и вектор изменения скорости. Таким образом, если ускорение постоянно, то его можно истолковать как изменение скорости в единицу времени. Это позволяет установить единицы модуля ускорения и его проекций.

Запишем выражение для модуля ускорения:

Отсюда следует, что:
модуль ускорения численно равен единице, если за единицу времени модуль вектора изменения скорости изменяется на единицу.
Если время измерено в секундах, а скорость - в метрах в секунду, то единица ускорения - м/с 2 (метр на секунду в квадрате).

При прямолинейном равноускоренном движении тело

двигается вдоль условной прямой линии,
его скорость постепенно увеличивается или уменьшается,
за равные промежутки времени скорость меняется на равную величину.

Например, автомобиль из состояния покоя начинает двигаться по прямой дороге, и до скорости, скажем, в 72 км/ч он двигается равноускоренно. Когда заданная скорость достигнута, то авто движется без изменения скорости, т. е. равномерно. При равноускоренном движении его скорость возрастала от 0 до 72 км/ч. И пусть за каждую секунду движения скорость увеличивалась на 3,6 км/ч. Тогда время равноускоренного движения авто будет равно 20 секундам. Поскольку ускорение в СИ измеряется в метрах на секунду в квадрате, то надо ускорение 3,6 км/ч за секунду перевести в соответствующие единицы измерения. Оно будет равно (3,6 * 1000 м) / (3600 с * 1 с) = 1 м/с 2 .

Допустим, через какое-то время езды с постоянной скоростью автомобиль начал тормозить, чтобы остановиться. Движение при торможении тоже было равноускоренным (за равные промежутки времени скорость уменьшалась на одинаковую величину). В данном случае вектор ускорения будет противоположен вектору скорости. Можно сказать, что ускорение отрицательно.

Итак, если начальная скорость тела нулевая, то его скорость через время в t секунд будет равно произведению ускорения на это время:

При падении тела «работает» ускорение свободного падения, и скорость тела у самой поверхности земли будет определяться по формуле:

Если известна текущая скорость тела и время, которое понадобилось, чтобы развить такую скорость из состояния покоя, то можно определить ускорение (т. е. как быстро менялась скорость), разделив скорость на время:

Однако тело могло начать равноускоренное движение не из состояния покоя, а уже обладая какой-то скоростью (или ему придали начальную скорость). Допустим, вы бросаете камень с башни вертикально вниз с приложением силы. На такое тело действует ускорение свободного падения, равное 9,8 м/с 2 . Однако ваша сила придала камню еще скорости. Таким образом, конечная скорость (в момент касания земли) будет складываться из скорости, развившийся в результате ускорения и начальной скорости. Таким образом, конечная скорость будет находиться по формуле:

Однако, если камень бросали вверх. То начальная его скорость направлена вверх, а ускорение свободного падения вниз. То есть вектора скоростей направлены в противоположные стороны. В этом случае (а также при торможении) произведение ускорения на время надо вычитать из начальной скорости:

Получим из этих формул формулы ускорения. В случае ускорения:

at = v – v 0
a = (v – v 0)/t

В случае торможения:

at = v 0 – v
a = (v 0 – v)/t

В случае, когда тело равноускоренно останавливается, то в момент остановки его скорость равна 0. Тогда формула сокращается до такого вида:

Зная начальную скорость тела и ускорение торможения, определяется время, через которое тело остановится:

Теперь выведем формулы для пути, которое тело проходит при прямолинейном равноускоренном движении . Графиком зависимость скорости от времени при прямолинейном равномерном движении является отрезок, параллельный оси времени (обычно берется ось x). Путь при этом вычисляется как площадь прямоугольника под отрезком. То есть умножением скорости на время (s = vt). При прямолинейном равноускоренном движении графиком является прямая, но не параллельная оси времени. Эта прямая либо возрастает в случае ускорения, либо убывает в случае торможения. Однако путь также определяется как площадь фигуры под графиком.

При прямолинейном равноускоренном движении эта фигура представляет собой трапецию. Ее основаниями являются отрезок на оси y (скорость) и отрезок, соединяющий точку конца графика с ее проекцией на ось x. Боковыми сторонами являются сам график зависимости скорости от времени и его проекция на ось x (ось времени). Проекция на ось x - это не только боковая сторона, но еще и высота трапеции, т. к. перпендикулярна его основаниям.

Как известно, площадь трапеции равна полусумме оснований на высоту. Длина первого основания равна начальной скорости (v 0), длина второго основания равна конечной скорости (v), высота равна времени. Таким образом получаем:

s = ½ * (v 0 + v) * t

Выше была дана формула зависимости конечной скорости от начальной и ускорения (v = v 0 + at). Поэтому в формуле пути мы можем заменить v:

s = ½ * (v 0 + v 0 + at) * t = ½ * (2v 0 + at) * t = ½ * t * 2v 0 + ½ * t * at = v 0 t + 1/2at 2

Итак, пройденный путь определяется по формуле:

s = v 0 t + at 2 /2

(К данной формуле можно прийти, рассматривая не площадь трапеции, а суммируя площади прямоугольника и прямоугольного треугольника, на которые разбивается трапеция.)

Если тело начало двигаться равноускоренно из состояния покоя (v 0 = 0), то формула пути упрощается до s = at 2 /2.

Если вектор ускорения был противоположен скорости, то произведение at 2 /2 надо вычитать. Понятно, что при этом разность v 0 t и at 2 /2 не должна стать отрицательной. Когда она станет равной нулю, тело остановится. Будет найден путь торможения. Выше была приведена формула времени до полной остановки (t = v 0 /a). Если подставить в формулу пути значение t, то путь торможения приводится к такой формуле.

Однако тело могло начать равноускоренное движение не из состояния покоя, а уже обладая какой-то скоростью (или ему придали начальную скорость). Допустим, вы бросаете камень с башни вертикально вниз с приложением силы. На такое тело действует ускорение свободного падения, равное 9,8 м/с2. Однако ваша сила придала камню еще скорости. Таким образом, конечная скорость (в момент касания земли) будет складываться из скорости, развившийся в результате ускорения и начальной скорости. Таким образом, конечная скорость будет находиться по формуле:

at = v – v0
a = (v – v0)/t

В случае торможения:

at = v0 – v
a = (v0 – v)/t

Теперь выведем

s = ½ * (v0 + v) * t

§ 5. Ускорение

Следующий шаг на пути к уравнениям движения - это введение величины, которая связана с изменением скорости движения. Естественно спросить: а как изменяется скорость движения? В предыдущих главах мы рассматривали случай, когда действующая сила приводила к изменению скорости. Бывают легковые машины, которые набирают с места за скорость . Зная это, мы можем определить, как изменяется скорость, но только в среднем. Займемся следующим более сложным вопросом: как узнать быстроту изменения скорости. Другими словами, на сколько метров в секунду изменяется скорость за . Мы уже установили, что скорость падающего тела изменяется со временем по формуле (см. табл. 8.4), а теперь хотим выяснить, насколько она изменяется за . Эта величина называется ускорением.

Таким образом, ускорение определяется как быстрота изменения скорости. Всем сказанным ранее мы уже достаточно подготовлены к тому, чтобы сразу записать ускорение в виде производной от скорости, точно так же как скорость записывается в виде производной от расстояния. Если теперь продифференцировать формулу , то получим ускорение падающего тела

(При дифференцировании этого выражения использовался результат, полученный нами раньше. Мы видели, что производная от равна просто (постоянной). Если же выбрать эту постоянную равной 9,8, то сразу находим, что производная от равна 9,8.) Это означает, что скорость падающего тела постоянно возрастает на за каждую секунду. Этот же результат можно получить и из табл. 8.4. Как видите, в случае падающего тела все получается довольно просто, но ускорение, вообще говоря, непостоянно. Оно получилось постоянным только потому, что постоянна сила, действующая на падающее тело, а по закону Ньютона ускорение должно быть пропорционально силе.

В качестве следующего примера найдем ускорение в той задаче, с которой мы уже имели дело при изучении скорости:

Для скорости мы получили формулу

Так как ускорение - это производная скорости по времени, то для того, чтобы найти его значение, нужно продифференцировать эту формулу. Вспомним теперь одно из правил табл. 8.3, а именно что производная суммы равна сумме производных. Чтобы продифференцировать первый из этих членов, мы но будем проделывать всю длинную процедуру, которую делали раньше, а просто напомним, что такой квадратичный член встречался нам при дифференцировании функции , причем в результате коэффициент удваивался, а превращалось в . Вы можете сами убедиться в том, что то же самое произойдет и сейчас. Таким образом, производная от будет равна . Перейдем теперь к дифференцированию второго слагаемого. По одному из правил табл. 8.3 производная от постоянной будет нулем, следовательно, этот член не даст в ускорение никакого вклада. Окончательный результат: .

Выведем еще две полезные формулы, которые получаются интегрированием. Если тело из состояния покоя движется с постоянным ускорением , то его скорость в любой момент времени будет равна

а расстояние, пройденное им к этому моменту времени,

Заметим еще, что поскольку скорость - это , а ускорение - производная скорости по времени, то можно написать

. (8.10)

Так что теперь мы знаем, как записывается вторая производная.

Существует, конечно, и обратная связь между ускорением и расстоянием, которая просто следует из того, что . Поскольку расстояние является интегралом от скорости, то оно может быть найдено двойным интегрированием ускорения. Все предыдущее рассмотрение было посвящено движению в одном измерении, а теперь мы коротко остановимся на движении в пространстве трех измерений. Рассмотрим движение частицы в трехмерном пространстве. Эта глава началась с обсуждения одномерного движения легковой машины, а именно с вопроса, на каком расстоянии от начала движения находится машина в различные моменты времени. Затем мы обсуждали связь между скоростью и изменением расстояния со временем и связь между ускорением и изменением скорости. Давайте в той же последовательности разберем движение в трех измерениях. Проще, однако, начать с более наглядного двумерного случая, а уж потом обобщить его на случай трех измерений. Нарисуем две пересекающиеся под прямым углом линии (оси координат) и будем задавать положение частицы в любой момент времени расстояниями от нее до каждой из осей. Таким образом, положение частицы задается двумя числами (координатами) и , каждое из которых является соответственно расстоянием до оси и до оси (фиг. 8.3). Теперь мы можем описать движение, составляя, например, таблицу, в которой эти две координаты заданы как функции времени. (Обобщение на трехмерный случай требует введения еще одной оси, перпендикулярной двум первым, и измерения еще одной координаты . Однако теперь расстояния берутся не до осей, а до координатных плоскостей.) Как определить скорость частицы? Для этого мы сначала найдем составляющие скорости по каждому направлению, или ее компоненты. Горизонтальная составляющая скорости, или -компонента, будет равна производной по времени от координаты , т. е.

а вертикальная составляющая, или -компонента, равна

В случае трех измерений необходимо еще добавить

Фигура 8.3. Описание движения тела на плоскости и вычисление его скорости.

Как, зная компоненты скорости, определить полную скорость в направлении движения? Рассмотрим в двумерном случае два последовательных положения частицы, разделенных коротким интервалом времени и расстоянием . Из фиг. 8.3 видно, что

(8.14)

(Значок соответствует выражению «приблизительно равно».) Средняя скорость в течение интервала получается простым делением: . Чтобы найти точную скорость в момент , нужно, как это уже делалось в начале главы, устремить к нулю. В результате оказывается, что

. (8.15)

В трехмерном случае точно таким же способом можно получить

(8.16)

Фигура 8.4. Парабола, которую описывает падающее тело, брошенное с горизонтальной начальной скоростью.

Ускорения мы определяем таким же образом, как и скорости: -компонента ускорения определяется как производная от -компоненты скорости (т. е. - вторая производная по времени) и т. д.

Давайте рассмотрим еще один интересный пример смешанного движения на плоскости. Пусть шарик движется в горизонтальном направлении с постоянной скоростью и в то же время падает вертикально вниз с постоянным ускорением . Что это за движение? Так как и, следовательно, скорость постоянна, то

а поскольку ускорение движения вниз постоянно и равно - , то координата падающего шара дается формулой

Какую же кривую описывает наш шарик, т. е. какая связь между координатами и ? Из уравнения (8.18), согласно (8.17), можно исключить время, поскольку 1=*х/и% после чего находим

Равномерно ускоренное движение без начальной скорости

Эту связь между координатами и можно рассматривать как уравнение траектории движения шарика. Вели изобразить ее графически, то получим кривую, которая называется параболой (фиг. 8.4). Так что любое свободно падающее тело, будучи брошенным в некотором направлении, движется по параболе.

При прямолинейном равноускоренном движении тело

двигается вдоль условной прямой линии,
его скорость постепенно увеличивается или уменьшается,
за равные промежутки времени скорость меняется на равную величину.

Однако тело могло начать равноускоренное движение не из состояния покоя, а уже обладая какой-то скоростью (или ему придали начальную скорость).

Допустим, вы бросаете камень с башни вертикально вниз с приложением силы. На такое тело действует ускорение свободного падения, равное 9,8 м/с2. Однако ваша сила придала камню еще скорости. Таким образом, конечная скорость (в момент касания земли) будет складываться из скорости, развившийся в результате ускорения и начальной скорости. Таким образом, конечная скорость будет находиться по формуле:

Получим из этих формул формулы ускорения. В случае ускорения:

at = v – v0
a = (v – v0)/t

В случае торможения:

at = v0 – v
a = (v0 – v)/t

Зная начальную скорость тела и ускорение торможения, определяется время, через которое тело остановится:

Как найти ускорение, зная путь и время?

То есть умножением скорости на время (s = vt). При прямолинейном равноускоренном движении графиком является прямая, но не параллельная оси времени. Эта прямая либо возрастает в случае ускорения, либо убывает в случае торможения. Однако путь также определяется как площадь фигуры под графиком.

Как известно, площадь трапеции равна полусумме оснований на высоту. Длина первого основания равна начальной скорости (v0), длина второго основания равна конечной скорости (v), высота равна времени. Таким образом получаем:

s = ½ * (v0 + v) * t

Выше была дана формула зависимости конечной скорости от начальной и ускорения (v = v0 + at). Поэтому в формуле пути мы можем заменить v:

s = ½ * (v0 + v0 + at) * t = ½ * (2v0 + at) * t = ½ * t * 2v0 + ½ * t * at = v0t + 1/2at2

Итак, пройденный путь определяется по формуле:

Если тело начало двигаться равноускоренно из состояния покоя (v0 = 0), то формула пути упрощается до s = at2/2.

Если вектор ускорения был противоположен скорости, то произведение at2/2 надо вычитать. Понятно, что при этом разность v0t и at2/2 не должна стать отрицательной. Когда она станет равной нулю, тело остановится. Будет найден путь торможения. Выше была приведена формула времени до полной остановки (t = v0/a). Если подставить в формулу пути значение t, то путь торможения приводится к такой формуле:

I. Механика

Физика->Кинематика->равноускоренное движение->

Тестирование онлайн

Равноускоренное движение

В этой теме мы рассмотрим очень особенный вид неравномерного движения. Исходя из противопоставления равномерному движению, неравномерное движение — это движение с неодинаковой скоростью, по любой траектории. В чем особенность равноускоренного движения? Это неравномерное движение, но которое "равно ускоряется" . Ускорение у нас ассоциируется с увеличением скорости. Вспомним про слово "равно", получим равное увеличение скорости. А как понимать "равное увеличение скорости", как оценить скорость равно увеличивается или нет? Для этого нам потребуется засечь время, оценить скорость через один и тот же интервал времени. Например, машина начинает двигаться, за первые две секунды она развивает скорость до 10 м/с, за следующие две секунды 20 м/с, еще через две секунды она уже двигается со скоростью 30 м/с. Каждые две секунды скорость увеличивается и каждый раз на 10 м/с. Это и есть равноускоренное движение.

Физическая величина, характеризующая то, на сколько каждый раз увеличивается скорость называется ускорением.

Можно ли движение велосипедиста считать равноускоренным, если после остановки в первую минуту его скорость 7км/ч, во вторую — 9км/ч, в третью 12км/ч? Нельзя! Велосипедист ускоряется, но не одинаково, сначала ускорился на 7км/ч (7-0), потом на 2 км/ч (9-7), затем на 3 км/ч (12-9).

Обычно движение с возрастающей по модулю скоростью называют ускоренным движением. Движение же с убывающей скоростью — замедленным движением. Но физики любое движение с изменяющейся скоростью называют ускоренным движением. Трогается ли автомобиль с места (скорость растет!), или тормозит (скорость уменьшается!), в любом случае он движется с ускорением.

Равноускоренное движение — это такое движение тела, при котором его скорость за любые равные промежутки времени изменяется (может увеличиваться или уменьшаться) одинаково

Ускорение тела

Ускорение характеризует быстроту изменения скорости. Это число, на которое изменяется скорость за каждую секунду. Если ускорение тела по модулю велико, это значит, что тело быстро набирает скорость (когда оно разгоняется) или быстро теряет ее (при торможении). Ускорение — это физическая векторная величина, численно равная отношению изменения скорости к промежутку времени, в течение которого это изменение произошло.

Определим ускорение в следующей задаче. В начальный момент времени скорость теплохода была 3 м/с, в конце первой секунды скорость теплохода стала 5 м/с, в конце второй — 7м/с, в конце третьей 9 м/с и т.д. Очевидно, . Но как мы определили? Мы рассматриваем разницу скоростей за одну секунду. В первую секунду 5-3=2, во вторую секунду 7-5=2, в третью 9-7=2. А как быть, если скорости даны не за каждую секунду? Такая задача: начальная скорость теплохода 3 м/с, в конце второй секунды — 7 м/с, в конце четвертой 11 м/с.В этом случае необходимо 11-7= 4, затем 4/2=2. Разницу скоростей мы делим на промежуток времени.

Эту формулу чаще всего при решении задач применяют в видоизмененном виде:

Формула записана не в векторном виде, поэтому знак "+" пишем, когда тело ускоряется, знак "-" — когда замедляется.

Направление вектора ускорения

Направление вектора ускорения изображено на рисунках

На этом рисунке машина движется в положительном направлении вдоль оси Ox, вектор скорости всегда совпадает с направлением движения (направлен вправо).

Как найти ускорение зная начальную и конечную скорость и путь?

Когда вектор ускорение совпадает с направлением скорости, это означает, что машина разгоняется. Ускорение положительное.

При разгоне направление ускорения совпадает с направлением скорости. Ускорение положительное.

На этом рисунке машина движется в положительном направлении по оси Ox, вектор скорости совпадает с направлением движения (направлен вправо), ускорение НЕ совпадает с направлением скорости, это означает, что машина тормозит. Ускорение отрицательное.

При торможении направление ускорения противоположно направлению скорости. Ускорение отрицательное.

Разберемся, почему при торможении ускорение отрицательное. Например, теплоход за первую секунду сбросил скорость с 9м/с до 7м/с, за вторую секунду до 5м/с, за третью до 3м/с. Скорость изменяется на "-2м/с". 3-5=-2; 5-7=-2; 7-9=-2м/с. Вот откуда появляется отрицательное значение ускорения.

При решении задач, если тело замедляется, ускорение в формулы подставляется со знаком "минус"!!!

Перемещение при равноускоренном движении

Дополнительная формула, которую называют безвременной

Формула в координатах

Связь со средней скоростью

При равноускоренном движении среднюю скорость можно рассчитывать как среднеарифметическое начальной и конечной скорости

Из этого правила следует формула, которую очень удобно использовать при решении многих задач

Соотношение путей

Если тело движется равноускоренно, начальная скорость нулевая, то пути, проходимые в последовательные равные промежутки времени, относятся как последовательный ряд нечетных чисел.

Главное запомнить

1) Что такое равноускоренное движение;
2) Что характеризует ускорение;
3) Ускорение — вектор. Если тело разгоняется ускорение положительное, если замедляется — ускорение отрицательное;
3) Направление вектора ускорения;
4) Формулы, единицы измерения в СИ

Упражнения

Два поезда идут навстречу друг другу: один — ускоренно на север, другой — замедленно на юг. Как направлены ускорения поездов?

Одинаково на север. Потому что у первого поезда ускорение совпадает по направлению с движением, а у второго — противоположное движению (он замедляется).

Поезд движется равноускоренно с ускорением a (a>0). Известно, что к концу четвертой секунды скорость поезда равна 6м/с. Что можно сказать о величине пути, пройденном за четвертую секунду? Будет ли этот путь больше, меньше или равен 6м?

Так как поезд движется с ускорением, то скорость его все время возрастает (a>0). Если к концу четвертой секунды скорость равна 6м/с, то в начале четвертой секунды она была меньше 6м/с. Следовательно, путь, пройденный поездом за четвертую секунду, меньше 6м.

Какие из приведенных зависимостей описывают равноускоренное движение?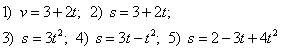

Уравнение скорости движущегося тела . Каково соответствующее уравнение пути?

* Автомобиль прошел за первую секунду 1м, за вторую секунду 2м, за третью секунду 3м, за четвертую секунду 4м и т.д. Можно ли считать такое движение равноускоренным?

В равноускоренном движении пути, проходимые в последовательные равные промежутки времени, относятся как последовательный ряд нечетных чисел. Следовательно, описанное движение не равноускоренное.

К примеру, автомобиль, который трогается с места, движется ускоренно, так как наращивает скорость движения. В точке начала движения скорость автомобиля равняется нулю. Начав движение, автомобиль разгоняется до некоторой скорости. При необходимости затормозить, автомобиль не сможет остановиться мгновенно, а за какое-то время. То есть скорость автомобиля будет стремиться к нулю - автомобиль начнет двигаться замедленно до тех пор, пока не остановится полностью. Но физика не имеет термина «замедление». Если тело двигается, уменьшая скорость, этот процесс тоже называется ускорением , но со знаком «-».

Средним ускорением называется отношение изменения скорости к промежутку времени, за который это изменении произошло. Вычисляют среднее ускорение при помощи формулы:

где - это . Направление вектора ускорения такое же, как у направления изменения скорости Δ = - 0

где 0 является начальной скоростью. В момент времени t 1 (см. рис. ниже) у тела 0 . В момент времени t 2 тело имеет скорость . Исходя из правила вычитания векторов, определим вектор изменения скорости Δ = - 0 . Отсюда вычисляем ускорение:

В системе СИ единицей ускорения называется 1 метр в секунду за секунду (либо метр на секунду в квадрате):

Метр на секунду в квадрате - это ускорение прямолинейно движущейся точки, при котором за 1 с скорость этой точки растет на 1 м/с. Другими словами, ускорение определяет степень изменения скорости тела за 1 с. К примеру, если ускорение составляет 5 м/с 2 , значит, скорость тела ежесекундно растет на 5 м/с.

Мгновенное ускорение тела (материальной точки) в данный момент времени - это физическая величина , которая равна пределу, к которому стремится среднее ускорение при стремлении промежутка времени к 0. Другими словами - это ускорение, развиваемое телом за очень маленький отрезок времени:

Ускорение имеет такое же направление, как и изменение скорости Δ в крайне маленьких промежутках времени, за которые скорость изменяется. Вектор ускорения можно задать при помощи проекций на соответствующие оси координат в заданной системе отсчета (проекциями а Х, a Y , a Z).

При ускоренном прямолинейном движении скорость тела увеличивается по модулю, т.е. v 2 > v 1 , а вектор ускорения имеет такое же направление, как и у вектора скорости 2 .

Если скорость тела по модулю уменьшается (v 2 < v 1), значит, у вектора ускорения направление противоположно направлению вектора скорости 2 . Другими словами, в таком случае наблюдаем замедление движения (ускорение отрицательно, а < 0). На рисунке ниже изображено направление векторов ускорения при прямолинейном движении тела для случая ускорения и замедления.

Если происходит движение по криволинейной траектории, то изменяется модуль и направление скорости. Значит, вектор ускорения изображают в виде 2х составляющих.

Тангенциальным (касательным) ускорением называют ту составляющую вектора ускорения, которая направлена по касательной к траектории в данной точке траектории движения. Тангенциальное ускорение описывает степень изменения скорости по модулю при совершении криволинейного движения.

У вектора тангенциального ускорения τ (см. рис. выше) направление такое же, как и у линейной скорости либо противоположно ему. Т.е. вектор тангенциального ускорения находится в одной оси с касательной окружности, являющейся траекторией движения тела.

Содержимое:

Ускорение характеризует быстроту изменения скорости движущегося тела. Если скорость тела остается постоянной, то оно не ускоряется. Ускорение имеет место только в том случае, когда скорость тела меняется. Если скорость тела увеличивается или уменьшается на некоторую постоянную величину, то такое тело движется с постоянным ускорением. Ускорение измеряется в метрах в секунду за секунду (м/с 2) и вычисляется по значениям двух скоростей и времени или по значению силы, приложенной к телу.

Шаги

1 Вычисление среднего ускорения по двум скоростям

1 Формула для вычисления среднего ускорения. Среднее ускорение тела вычисляется по его начальной и конечной скоростям (скорость – это быстрота передвижения в определенном направлении) и времени, которое необходимо телу для достижения конечной скорости. Формула для вычисления ускорения: a = Δv / Δt , где а – ускорение, Δv – изменение скорости, Δt – время, необходимое для достижения конечной скорости.
- Единицами измерения ускорения являются метры в секунду за секунду, то есть м/с 2 .
- Ускорение является векторной величиной, то есть задается как значением, так и направлением. Значение – это числовая характеристика ускорения, а направление – это направление движения тела. Если тело замедляется, то ускорение будет отрицательным.
2 Определение переменных. Вы можете вычислить Δv и Δt следующим образом: Δv = v к - v н и Δt = t к - t н , где v к – конечная скорость, v н – начальная скорость, t к – конечное время, t н – начальное время.
- Так как ускорение имеет направление, всегда вычитайте начальную скорость из конечной скорости; в противно случае направление вычисленного ускорения будет неверным.
- Если в задаче начальное время не дано, то подразумевается, что t н = 0.
3 Найдите ускорение при помощи формулы. Для начала напишите формулу и данные вам переменные. Формула: . Вычтите начальную скорость из конечной скорости, а затем разделите результат на промежуток времени (изменение времени). Вы получите среднее ускорение за данный промежуток времени.
- Если конечная скорость меньше начальной, то ускорение имеет отрицательное значение, то есть тело замедляется.
- Пример 1: автомобиль разгоняется с 18,5 м/с до 46,1 м/с за 2,47 с. Найдите среднее ускорение.
  - Напишите формулу: a = Δv / Δt = (v к - v н)/(t к - t н)
  - Напишите переменные: v к = 46,1 м/с, v н = 18,5 м/с, t к = 2,47 с, t н = 0 с.
  - Вычисление: a = (46,1 - 18,5)/2,47 = 11,17 м/с 2 .
- Пример 2: мотоцикл начинает торможение при скорости 22,4 м/с и останавливается через 2,55 с. Найдите среднее ускорение.
  - Напишите формулу: a = Δv / Δt = (v к - v н)/(t к - t н)
  - Напишите переменные: v к = 0 м/с, v н = 22,4 м/с, t к = 2,55 с, t н = 0 с.
  - Вычисление: а = (0 - 22,4)/2,55 = -8,78 м/с 2 .

2 Вычисление ускорения по силе

1 Второй закон Ньютона. Согласно второму закону Ньютона тело будет ускоряться, если силы, действующие на него, не уравновешивают друг друга. Такое ускорение зависит от результирующей силы, действующей на тело. Используя второй закон Ньютона, вы можете найти ускорение тела, если вам известна его масса и сила, действующая на это тело.
- Второй закон Ньютона описывается формулой: F рез = m x a , где F рез – результирующая сила, действующая на тело, m – масса тела, a – ускорение тела.
- Работая с этой формулой, используйте единицы измерения метрической системы, в которой масса измеряется в килограммах (кг), сила в ньютонах (Н), а ускорение в метрах в секунду за секунду (м/с 2).
2 Найдите массу тела. Для этого положите тело на весы и найдите его массу в граммах. Если вы рассматриваете очень большое тело, поищите его массу в справочниках или в интернете. Масса больших тел измеряется в килограммах.
- Для вычисления ускорения по приведенной формуле необходимо преобразовать граммы в килограммы. Разделите массу в граммах на 1000, чтобы получить массу в килограммах.
3 Найдите результирующую силу, действующую на тело. Результирующая сила не уравновешивается другими силами. Если на тело действуют две разнонаправленные силы, причем одна из них больше другой, то направление результирующей силы совпадает с направлением большей силы. Ускорение возникает тогда, когда на тело действует сила, которая не уравновешена другими силами и которая приводит к изменению скорости тела в направлении действия этой силы.
- Например, вы с братом перетягиваете канат. Вы тянете канат с силой 5 Н, а ваш брат тянет канат (в противоположном направлении) с силой 7 Н. Результирующая сила равна 2 Н и направлена в сторону вашего брата.
- Помните, что 1 Н = 1 кг∙м/с 2 .
4 Преобразуйте формулу F = ma так, чтобы вычислить ускорение. Для этого разделите обе стороны этой формулы на m (массу) и получите: a = F/m. Таким образом, для нахождения ускорения разделите силу на массу ускоряющегося тела.
- Сила прямо пропорциональна ускорению, то есть чем больше сила, действующая на тело, тем быстрее оно ускоряется.
- Масса обратно пропорциональна ускорению, то есть чем больше масса тела, тем медленнее оно ускоряется.
5 Вычислите ускорение по полученной формуле. Ускорение равно частному от деления результирующей силы, действующей на тело, на его массу. Подставьте данные вам значения в эту формулу, чтобы вычислить ускорение тела.
- Например: сила, равная 10 Н, действует на тело массой 2 кг. Найдите ускорение тела.
- a = F/m = 10/2 = 5 м/с 2

3 Проверка ваших знаний

1 Направление ускорения. Научная концепция ускорения не всегда совпадает с использованием этой величины в повседневной жизни. Помните, что у ускорения есть направление; ускорение имеет положительное значение, если оно направлено вверх или вправо; ускорение имеет отрицательное значение, если оно направлено вниз или влево. Проверьте правильность вашего решения, основываясь на следующей таблице:
2 Направление силы. Помните, что ускорение всегда сонаправлено силе, действующей на тело. В некоторых задачах даются данные, цель которых заключается в том, чтобы ввести вас в заблуждение.
- Пример: игрушечная лодка массой 10 кг движется на север с ускорением 2 м/с 2 . Ветер, дующий в западном направлении, действует на лодку с силой 100 Н. Найдите ускорение лодки в северном направлении.
- Решение: так как сила перпендикулярна направлению движения, то она не влияет на движение в этом направлении. Поэтому ускорение лодки в северном направлении не изменится и будет равно 2 м/с 2 .
3 Результирующая сила. Если на тело действуют сразу несколько сил, найдите результирующую силу, а затем приступайте к вычислению ускорения. Рассмотрим следующую задачу (в двумерном пространстве):
- Владимир тянет (справа) контейнер массой 400 кг с силой 150 Н. Дмитрий толкает (слева) контейнер с силой 200 Н. Ветер дует справа налево и действует на контейнер с силой 10 Н. Найдите ускорение контейнера.
- Решение: условие этой задачи составлено так, чтобы запутать вас. На самом деле все очень просто. Нарисуйте схему направления сил, так вы увидите, что сила в 150 Н направлена вправо, сила в 200 Н тоже направлена вправо, а вот сила в 10 Н направлена влево. Таким образом, результирующая сила равна: 150 + 200 - 10 = 340 Н. Ускорение равно: a = F/m = 340/400 = 0,85 м/с 2 .