Обыкновенные и десятичные дроби и действия над ними. Десятичные дроби и действия с ними. Деление и умножение десятичных дробей
§ 31. Задачи и примеры на все действия с десятичными дробями.
Выполнить указанные действия:

767. Найти частное от деления:

772. Вычислить:
Найти х , если:

776. Неизвестное число умножили на разность чисел 1 и 0,57 и в произведении получили 3,44. Найти неизвестное число.
777. Сумму неизвестного числа и 0,9 умножили на разность между 1 и 0,4 и в произведении получили 2,412. Найти неизвестное число.
778. По данным диаграммы о выплавке чугуна в РСФСР (рис. 36) составить задачу, для решения которой надо применить действия сложения, вычитания и деления.

779. 1) Длина Суэцкого канала 165,8 км, длина Панамского канала меньше Суэцкого на 84,7 км, а длина Беломорско-Балтийского канала на 145,9 км больше длины Панамского. Какова длина Беломорско-Балтийского канала?
2) Московское метро (к 1959 г.) было построено в 5 очередей. Длина первой очереди метро 11,6 км, второй -14,9 км, длина третьей на 1,1 км меньше длины второй очереди, длина четвёртой очереди на 9,6 км больше третьей очереди, а длина пятой очереди на 11,5 км меньше четвёртой. Чему равна длина Московского метро к началу 1959 г.?
780. 1) Наибольшая глубина Атлантического океана 8,5 км, наибольшая глубина Тихого ркеана на 2,3 км больше глубины Атлантического океана, а наибольшая глубина Северного Ледовитого океана в 2 раза меньше наибольшей глубины Тихого океана. Какова наибольшая глубина Северного Ледовитого океана?
2) Автомобиль «Москвич» на 100 км пути расходует 9 л бензина, автомобиль «Победа» на 4,5 л больше, чем расходует «Москвич», а «Волга» в 1,1 раза больше «Победы». Сколько бензина расходует автомобиль «Волга» на 1 км пути? (Ответ округлить с точностью до 0,01 л.)
781. 1) Ученик во время каникул поехал к дедушке. По железной дороге он ехал 8,5 часа, а от станции на лошадях 1,5 часа. Всего он проехал 440 км. С какой скоростью ученик ехал по железной дороге, если на лошадях он ехал со скоростью 10 км в час?
2) Колхознику надо было быть в пункте, находящемся на расстоянии 134,7 км от его дома. 2,4 часа он ехал на автобусе со средней скоростью 55 км в час, а остальную часть пути он прошёл пешком со скоростью 4,5 км в час. Сколько времени он шёл пешком?
782. 1) За лето один суслик уничтожает около 0,12 ц хлеба. Пионеры весной истребили на 37,5 га 1 250 сусликов. Сколько хлеба сохранили школьники для колхоза? Сколько сбережённого хлеба приходится на 1 га?
2) Колхоз подсчитал, что, уничтожив сусликов на площади в 15 га пашни, школьники сберегли 3,6 т зерна. Сколько сусликов в среднем уничтожено на 1 га земли, если один суслик за лето уничтожает 0,012 т зерна?
783. 1) При размоле пшеницы на муку теряется 0,1 её веса, а при выпечке получается припёк, равный 0,4 веса муки. Сколько печёного хлеба получится из 2,5 т пшеницы?
2) Колхоз собрал 560 т семян подсолнуха. Сколько подсолнечного масла изготовят из собранного зерна, если вес зерна составляет 0,7 веса семян подсолнуха, а вес полученного масла составляет 0,25 веса зерна?
784. 1) Выход сливок из молока составляет 0,16 веса молока, а выход масла из сливок составляет 0,25 веса сливок. Сколько требуется молока (по весу) для получения 1 ц масла?
2) Сколько килограммов белых грибов надо собрать для получения 1 кг сушёных, если при подготовке к сушке остаётся 0,5 веса, а при сушке остаётся 0,1 веса обработанного гриба?
785. 1) Земля, отведённая колхозу, использована так: 55% её занято пашней, 35% -лугом, а вся остальная земля в количестве 330,2 га отведена под колхозный сад и под усадьбы колхозников. Сколько всего земли в колхозе?
2) Колхоз засеял 75% всей посевной площади зерновыми культурами, 20% -овощными, а остальную площадь кормовыми травами. Сколько посевной площади имел колхоз, если кормовыми травами он засеял 60 га?
786. 1) Сколько центнеров семян потребуется для засева поля, имеющего форму прямоугольника длиной 875 м и шириной 640 м, если на 1 га высевать 1,5 ц семян?
2) Сколько центнеров семян потребуется для засева поля, имеющего форму прямоугольника, если его периметр равен 1,6 км? Ширина поля 300 м. На засев 1 га требуется 1,5 ц семян.
787. Сколько пластинок квадратной формы со стороной в 0,2 дм поместится в прямоугольнике размером 0,4 дм х 10 дм?
788. Читальный зал имеет размеры 9,6 м х 5м х 4,5 м. На сколько мест рассчитан читальный зал, если на каждого человека необходимо 3 куб. м воздуха?
789. 1) Какую площадь луга скосит трактор с прицепом четырёх косилок за 8 час, если ширина захвата каждой косилки 1,56 м и скорость трактора 4,5 км в час? (Время на остановки не учитывается.) (Ответ округлить с точностью до 0,1 га.)
2) Ширина захвата тракторной овощной сеялки равна 2,8 м. Какую площадь можно засеять этой сеялкой за 8 час. работы при скорости 5 км в час?
790. 1) Найти выработку трёхкорпусного тракторного плуга за 10 час. работы, если скорость трактора 5 км в час, захват одного корпуса 35 см, а непроизводительная трата времени составила 0,1 всего затраченного времени. (Ответ округлить с точностью до 0,1 га.)
2) Найти выработку пятикорпусного тракторного плуга за 6 час. работы, если скорость трактора 4,5 км в час, захват одного корпуса 30 см, а непроизводительная трата времени составила 0,1 всего затраченного времени. (Ответ округлить с точностью до 0,1 га.)
791. Расход воды на 5 км пробега для паровоза пассажирского поезда равен 0,75 т. Водяной бак тендера вмещает 16,5 т воды. На сколько километров пути хватит воды поезду, если бак был наполнен на 0,9 своей вместимости?
792. На запасном пути могут поместиться только 120 товарных вагонов при средней длине вагона в 7,6 м. Сколько поместится на этом пути четырёхосных пассажирских вагонов длиной в 19,2 м каждый, если на этом пути будут помещены ещё 24 товарных вагона?
793. Для прочности железнодорожной насыпи рекомендуется производить укрепление откосов посредством посева полевых трав. На каждый квадратный метр насыпи требуется 2,8 г семян стоимостью 0,25 руб. за 1 кг. Сколько будет стоить засев 1,02 га откосов, если стоимость работ составит 0,4 от стоимости семян? (Ответ округлить с точностью до 1 руб.)
794. Кирпичный завод доставил на станцию железной дороги кирпичи. На перевозке кирпичей работали 25 лошадей и 10 грузовых машин. Каждая лошадь перевозила 0,7 т за одну поездку и в день совершала 4 поездки. Каждая машина перевозила за одну поездку 2,5 т и в день совершала 15 поездок. Перевозка продолжалась 4 дня. Сколько штук кирпичей было доставлено на станцию, если средний вес одного кирпича 3,75 кг? (Ответ округлить с точностью до 1 тыс. штук.)
795. Запас муки был распределён между тремя пекарнями: первая получила 0,4 всего запаса, вторая 0,4 остатка, а третья пекарня получила муки на 1,6 т меньше, чем первая. Сколько всего муки было распределено?
796. На втором курсе института 176 студентов, на третьем 0,875 этого числа, а на первом в полтора раза больше того, что было на третьем курсе. Число студентов на первом, втором и третьем курсах составляло 0,75 всего числа студентов этого института. Сколько студентов было в институте?
___________
797. Найти среднее арифметическое:
1) двух чисел: 56,8 и 53,4; 705,3 и 707,5;
2) трёх чисел: 46,5; 37,8 и 36; 0,84; 0,69 и 0,81;
3) четырёх чисел: 5,48; 1,36; 3,24 и 2,04.
798. 1) Утром температура была 13,6°, в полдень 25,5°, а вечером 15,2°. Вычислить среднюю температуру за этот день.
2) Какова средняя температура за неделю, если в течение недели термометр показал: 21°; 20,3°; 22,2°; 23,5°; 21,1°; 22,1°; 20,8°?
799. 1) Школьная бригада в первый день прополола 4,2 га свёклы, во второй день 3,9 га, а в третий 4,5 га. Определять среднюю выработку бригады за день.
2) Для установления нормы времени на изготовление новой детали были поставлены 3 токаря. Первый изготовил деталь за 3,2 мин., второй за 3,8 мин., а третий за 4,1 мин. Вычислить норму времени, которая была установлена на изготовление детали.
800. 1) Среднее арифметическое двух чисел 36,4. Одно из этих чисел 36,8. Найти другое.
2) Температуру воздуха измеряли три раза в день: утром, в полдень и вечером. Найти температуру воздуха утром, если в полдень было 28,4°, вечером 18,2° тепла, а средняя температура дня 20,4°.
801. 1) Автомобиль проехал за первые два часа 98,5 км, а за последующие три часа 138 км. Сколько километров в среднем проезжал автомобиль в час?
2) Пробный улов и взвешивание карпов-годовичков показал, что из 10 карпов 4 имели вес по 0,6 кг, 3 по 0,65 кг, 2 по 0,7 кг и 1 весил 0,8 кг. Каков в среднем вес карпа-годовичка?
802. 1) К 2 л сиропа стоимостью 1,05 руб. за 1 л добавили 8 л воды. Сколько стоит 1 л полученной воды с сиропом?
2) Хозяйка купила банку консервированного борща объёмом 0,5 л за 36 коп. и прокипятила с 1,5 л воды. Во что обошлась тарелка борща, если её объём равен 0,5 л?
803. Лабораторная работа «Измерение расстояния между двумя точками»,
1-й приём. Измерение рулеткой (мерной лентой). Класс разбивается на звенья по три человека в каждом. Принадлежности: 5-6 вех и 8-10 бирок.
Ход выполнения работы: 1) отмечаются точки А и Б и между ними провешивают прямую (см. задачу 178); 2) укладывают рулетку, вдоль провешенной прямой и каждый раз отмечают биркой конец рулетки. 2-й приём. Измерение, шагами. Класс разбивается на звенья по три человека в каждом. Каждый учащийся проходит расстояние от А до Б, считая число своих шагов. Умножив среднюю длину своего шага на полученное число шагов, находят расстояние от А до Б.
3-й приём. Измерение "на глаз" . Каждый из учащихся вытягивает левую руку с поднятым большим пальцем (рис. 37) и направляет большой палец на веху в точку Б (на рисунке - дерево) так, чтобы левый глаз (точка А), большой палец и точка Б находились на одной прямой. Не изменяя положения, закрывают левый глаз и смотрят правым на большой палец. Измеряют на глаз полученное смещение и увеличивают его в 10 раз. Это и есть расстояние от А до Б.

_________________
804. 1) По переписи 1959 г. население СССР составляло 208,8 млн. человек, причем сельского населения было на 9,2 млн. человек больше, чем городского. Сколько было городского и сколько сельского населения в СССР в 1959 г.?
2) По переписи 1913 г. население России составляло 159,2 млн. человек, причём городского населения было на 103,0 млн. человек меньше, чем сельского. Сколько было городского и сельского населения в России в 1913 г.?
805. 1) Длина проволоки 24,5 м. Эту проволоку разрезали на две части так, что первая часть получилась на 6,8 м длиннее, чем вторая. Сколько метров длины имеет каждая часть?
2) Сумма двух чисел 100,05. Одно число на 97,06 больше другого. Найти эти числа.
806. 1) На трёх угольных складах 8656,2 т угля, на втором складе на 247,3 т угля больше, чем на первом, а на третьем на 50,8 т больше, чем на втором. Сколько тонн угля на каждом складе?
2) Сумма трёх чисел 446,73. Первое число меньше второго на 73,17 и больше третьего на 32,22. Найти эти числа.
807. 1) Катер по течению реки шёл со скоростью 14,5 км в час, а против течения со скоростью 9,5 км в час. Какова скорость катера в стоячей воде и какова скорость течения реки?
2) Пароход прошёл за 4 часа по течениию реки 85,6 км, а против течения за 3 часа 46,2 км. Какова скорость парохода в стоячей воде и какова скорость течения реки?
_________
808. 1) Два парохода доставили 3 500 т груза, причём один пароход доставил в 1,5 раза груза больше, чем другой. Сколько груза доставил каждый пароход?
2) Площадь двух комнат 37,2 кв. м. Площадь одной комнаты в 2 раза больше другой. Чему равна площадь каждой комнаты?
809. 1) Из двух населённых пунктом, расстояние между которыми 32,4 км одновременно выехали навстречу друг другу мотоциклист и велосипедист. Сколько километров проедет каждый из них до встречи, если скорость мотоциклиста в 4 раза больше скорости велосипедиста?
2) Найти два числа, сумма которых 26,35, а частное от деления одного числа на другое равно 7,5.
810. 1) Завод отправил три вида груза общим весом в 19,2 т. Вес груза первого вида был втрое больше веса груза второго вида, а вес груза третьего вида был вдвое меньше, чем вес груза первого и второго видов вместе. Каков вес груза каждого вида?
2) За три месяца бригада горняков добыла 52,5 тыс. т железной руды. За март добыто в 1,3, за февраль в 1,2 раза больше, чем за январь. Сколько руды добывала бригада ежемесячно?
811. 1) Газопровод Саратов - Москва на 672 км длиннее канала имени Москвы. Найти длину того и другого сооружения, если длина газопровода в 6,25 раза больше длины канала имени Москвы.
2) Длина реки Дона в 3,934 раза больше длины реки Москвы. Найти длину каждой реки, если длина реки Дона больше длины реки Москвы на 1 467 км.
812. 1) Разность двух чисел 5,2, а частное от деления одного числа на другое 5. Найти эти числа.
2) Разность двух чисел 0,96, а их частное 1,2. Найти эти числа.
813. 1) Одно число на 0,3 меньше другого и составляет 0,75 его. Найти эти числа.
2) Одно число на 3,9 больше другого числа. Если меньшее число увеличить в 2 раза, то оно составит 0,5 от большего. Найти эти числа.
814. 1) Колхоз засеял пшеницей и рожью 2600 га земли. Сколько гектаров земли было засеяно пшеницей и сколько рожью, если 0,8 площади, засеянной пшеницей, равны 0,5 площади, засеянной рожью?
2) Коллекция двух мальчиков вместе составляет 660 марок. Из скольких марок состоит коллекция каждого мальчика, если 0,5 числа марок первого мальчика равны 0,6 числа марок коллекции второго мальчика?
815. Два ученика вместе имели 5,4 руб. После того как первый истратил 0,75 своих денег, а второй 0,8 своих денег, у них осталось денег поровну. Сколько денег было у каждого ученика?
816. 1) Два парохода вышли навстречу друг другу из двух портов, расстояние между которыми 501,9 км. Через сколько времени они встретятся, если скорость первого парохода 25,5 км в час, а скорость второго 22,3 км в час?
2) Два поезда вышли навстречу друг другу из двух пунктов, расстояние между которыми 382,2 км. Через сколько времени они встретятся, если средняя скорость первого поезда была 52,8 км в час, а второго 56,4 км в час?
817. 1) Из двух городов, расстояние между которыми 462 км, одновременно выехали два автомобиля и встретились через 3,5 часа. Найти скорость каждого автомобиля, если скорость первого была на 12 км в час больше скорости второго автомобиля.
2) Из двух населённых пунктов, расстояние между которыми 63 км, одновременно выехали навстречу друг другу мотоциклист и велосипедист и встретились через 1,2 часа. Найти скорость мотоциклиста, если велосипедист ехал со скоростью на 27,5 км в час меньшей скорости мотоциклиста.
818. Ученик заметил, что поезд, состоящий из паровоза и 40 вагонов, проходил мимо него 35 сек. Определить скорость поезда в час, если длина паровоза 18,5 м, а длина вагона 6,2 м. (Ответ дать с точностью до 1 км в час.)
819. 1) Из А в Б выехал велосипедист со средней скоростью 12,4 км в час. Спустя 3 часа 15 мин. из Б навстречу ему выехал другой велосипедист со средней скоростью 10,8 км в час. Через сколько часов и на каком расстоянии от А они встретятся, если 0,32 расстояния между А и Б равны 76 км?
2) Из городов А и Б, расстояние между которыми 164,7 км, выехали навстречу друг другу грузовая машина из города А и легковая - из города Б. Скорость грузовой машины 36 км, а легковой в 1,25 раза больше. Легковая машина вышла на 1,2 часа позже грузовой. Через сколько времени и на каком расстоянии от города Б легковая машина встретит грузовую?
820. Два парохода вышли одновременно из одного порта и идут в одном направлении. Первый пароход в каждые 1,5 часа проходит 37,5 км, а второй в каждые 2 часа проходит 45 км. Через сколько времени первый пароход будет находиться от второго на расстоянии 10 км?
821. Из одного пункта вначале вышел пешеход, а через 1,5 часа после его выхода выехал в том же направлении велосипедист. На каком расстоянии от пункта велосипедист догнал пешехода, если пешеход шёл со скоростью 4,25 км в час, а велосипедист ехал со скоростью 17 км в час?
822. Поезд вышел из Москвы в Ленинград в 6 час. 10 мин. утра и шёл со средней скоростью 50 км п час. Позднее из Москвы в Ленинград вылетел пассажирский самолет и прилетел в Ленинград одновременно с прибытием поезда. Средняя скорость самолёта была 325 км в час, а расстояние между Москвой и Ленинградом 650 км. Когда самолёт вылетел из Москвы?
823. Пароход по течению реки шёл 5 час, а против течения 3 часа и прошёл всего 165 км. Сколько километров он прошёл по течению и сколько против течении, если скорость течения реки 2,5 км в час?
824. Поезд вышел из А и должен прибыть в Б в определённое время; пройдя половину пути и делая по 0,8 км в 1 мин., поезд был остановлен на 0,25 часа; увеличив далее скорость на 100 м в 1 млн., поезд прибыл в Б вовремя. Найти расстояние между А и Б.
825. От колхоза до города 23 км. Из города в колхоз выехал на велосипеде почтальон со скоростью 12,5 км в час. Через 0,4 часа после этого ИВ колхоза в город выехал на лошади колхозник со скоростью, ранной 0,6 скорости почтальона. Через сколько времени после своего выезда колхозник встретит почтальона?
826. Из города А в город Б, отстоящий от А на 234 км, выехал автомобиль со скоростью 32 км в час. Через 1,75 часа после этого из города Б выехал навстречу первому второй автомобиль, скорость которого в 1,225 раза больше скорости первого. Через сколько часов после своего выезда второй автомобиль встретит первы
827. 1) Одна машинистка может перепечатать рукопись за 1,6 часа, а другая за 2,5 часа. За сколько времени обе машинистки перепечатают эту рукопись, работая совместно? (Ответ округлить с точностью до 0,1 часа.)
2) Бассейн наполняется двумя насосами различной мощности. Первый насос, работая один, может наполнить бассейн за 3,2 часа, а второй за 4 часа. За сколько времени наполнится бассейн при одновременной работе этих насосов? (Ответ округлить с точностью до 0,1.)
828. 1) Одна бригада может выполнить некоторый заказ за 8 дней. Другой на выполнение этого заказа требуется 0,5 времени первой. Третья бригада может выполнить этот заказ за 5 дней. За сколько дней будет выполнен весь заказ при совместной работе трёх бригад? (Ответ округлить с точностью до 0,1 дня.)
2) Первый рабочий может выполнить заказ за 4 часа, второй в 1,25 раза быстрее, а третий за 5 час. За сколько часов будет выполнен заказ при совместной работе трёх рабочих? (Ответ округлить с точностью до 0,1 часа.)
829. На уборке улицы работают две машины. Первая из них может убрать всю улицу за 40 мин., второй для этого требуется 75% времени первой. Обе машины начали работу одновременно. После совместной рвботы в течение 0,25 часа вторая машина прекратила работу. Во сколько времени после этого первая машина закончила работу по уборке улицы?
830. 1) Одна из сторон треугольника 2,25 см, вторая на 3,5 см больше первой, а третья на 1,25 см меньше второй. Найти периметр треугольника.
2) Одна из сторон треугольника 4,5 см, вторая на 1,4 см меньше первой, а третья сторона равна полусумме двух первых сторон. Чему равен периметр треугольника?
831 . 1) Основание треугольника 4,5 см, а высота его на 1,5 см меньше. Найти площадь треугольника.
2) Высота треугольника 4,25 см, а его основание в 3 раза больше. Найти площадь треугольника. (Ответ округлить с точностью до 0,1.)
832. Найти площади заштрихованных фигур (рис. 38).

833. Какая площадь больше: прямоугольника со сторонами 5 см и 4 см, квадрата со стороной 4,5 см или треугольника, основание и высота которого равны по 6 см?
834. Комната имеет длину 8,5 м, ширину 5,6 м и высоту 2,75 м. Площадь окон, дверей и печей составляет 0,1 общей площади стен комнаты. Сколько кусков обоев понадобится для оклеивания этой комнаты, если кусок обоев имеет длину 7 м и ширину 0,75 м? (Ответ округлить с точностью до 1 куска.)
835. Надо снаружи оштукатурить и побелить одноэтажный дом, размеры которого: длина 12 м, ширина 8 м и высота 4,5 м. В доме 7 окон размером каждое 0,75 м х 1,2 м и 2 двери каждая размером 0,75 м х 2,5 м. Сколько будет стоить вся работа, если побелка и штукатурка 1 кв. м стоит 24 коп.? (Ответ округлить а точностью до 1 руб.)
836. Вычислите поверхность и объём вашей комнаты. Размеры комнаты найдите измерением.
837. Огород имеет форму прямоугольника, длина которого 32 м, ширина 10 м. 0,05 всей площади огорода засеяно морковью, а остальная часть огорода засажена картофелем и луком, причём картофелем засажена площадь в 7 paз большая, чем луком. Сколько земли в отдельности засажено картофелем, луком и морковью?
838. Огород имеет форму прямоугольника, длина которого 30 м и ширина 12 м. 0,65 всей площади огорода засажено картофелем, а остальная часть - морковью и свёклой, причём свёклой засажено на 84 кв. м больше, чем морковью. Сколько земли в отдельности под картофелем, свёклой и морковью?
839. 1) Ящик, имеющий форму куба, обшили со всех сторон фанерой. Сколько фанеры израсходовано, если ребро куба 8,2 дм? (Ответ округлить с точностью до 0,1 кв. дм.)
2) Сколько краски потребуется для окраски куба с ребром в 28 см, если на 1 кв. см будет истрачено 0,4 г краски? (Ответ, округлить с точностью до 0,1 кг.)
840. Длина чугунной заготовки, имеющей форму прямоугольного параллелепипеда, равна 24,5 см, ширина 4,2 см и высота 3,8 см. Сколько весят 200 чугунных заготовок, если 1 куб. дм чугуна весит 7,8 кг? (Ответ округлить с точностью до 1 кг.)
841. 1) Длина ящика (с крышкой), имеющего форму прямоугольного параллелепипеда, равна 62,4 см, ширина 40,5 см, высота 30 см. Сколько квадратных метров досок пошло на изготовление ящика, если отходы досок составляют 0,2 поверхности, которая должна быть обшита досками? (Ответ округлить с точностью до 0,1 кв. м.)
2) Дно и боковые стенки ямы, имеющей форму прямоугольного параллелепипеда, должны быть обшиты досками. Длина ямы 72,5 м, ширина 4,6 м и высота 2,2 м. Сколько квадратных метров досок пошло на обшивку, если отходы досок составляют 0,2 поверхности, которая должна быть обшита досками? (Ответ округлить с точностью до 1 кв. м.)
842. 1) Длина подвала, имеющего форму прямоугольного параллелепипеда, равна 20,5 м, ширина 0,6 его длины, а высота 3,2 м. Подвал заполнили картофелем на 0,8 его объёма. Сколько тонн картофеля поместилось в подвале, если 1 куб.м картофеля весит 1,5 т? (Ответ округлить с точностью до 1 т.)
2) Длина бака, имеющего форму прямоугольного параллелепипеда, равна 2,5 м, ширина 0,4 его длины, а высота 1,4 м. Бак наполнен керосином на 0,6 его объёма. Сколько тонн керосина налито в бак, если вес керосина в объёме 1 куб. м равен 0,9 т? (Ответ округлить с точностью до 0,1 т.)
843. 1) Во сколько времени можно обновить воздух в комнате, имеющей 8,5 м длины, 6 м ширины и 3,2 м высоты, если через форточку в 1 сек. проходит 0,1 куб. м воздуха?
2) Произведите подсчёт времени, необходимого для обновления воздуха в вашей комнате.
844. Размеры бетонного блока для постройки стен следующие: 2,7 м х 1,4 м х 0,5 м. Пустота составляет 30% объёма блока. Сколько кубометров бетона потребуется на изготовление 100 таких блоков?
845. Грейдер-элеватор (машина для рытья канав) за 8 час. работы делает канаву шириной 30 см, глубиной 34 см и длиной 15 км. Скольких землекопов заменяет такая машина, если один землекоп может вынуть 0,8 куб. м в час? (Результат округлить.)
846. Закром в форме прямоугольного параллелепипеда имеет в длину 12 м и в ширину 8 ж. В этом закроме насыпано зерно до высоты 1,5 м. Для того чтобы узнать, сколько весит всё зерно, взяли ящик длиной 0,5 м, шириной 0,5 м и высотой 0,4 м, наполнили его зерном и взвесили. Сколько весило зерно в закроме, если зерно в ящике весило 80 кг?

849. Построить линейную диаграмму роста городского населения в СССР, если в 1913 г. городского населения было 28,1 млн человек, в 1926 г.-24,7 млн., в 1939 г.-56,1 млн. и в 1959г- 99,8 млн. человек.
850. 1) Составить смету на ремонт помещения вашего класса, если требуется побелить стены и потолок, а также покрасить пол. Данные для составления сметы (размеры класса, стоимость побелки 1 кв. м, стоимость покраски пола 1 кв. м) выяснить у завхоза школы.
2) Для посадки в саду школа купила саженцы: 30 яблонь по 0,65 руб. за штуку, 50 вишен по 0,4 руб. за штуку, 40 кустов крыжовника по 0,2 руб. и 100 кустов малины по 0,03 руб. за куст. Напишите счёт на эту покупку по образцу:

ОТВЕТЫ

При сложении десятичных дробей надо записать их одну под другой так, чтобы одинаковые разряды были друг под другом, а запятая - под запятой, и сложить дроби так, как складывают натуральные числа. Сложим, напрнмер, дроби 12,7 и 3,442. Первая дробь содержит одну цифру после запятой, а вторая - три. Чтобы выполнить сложение, преобразуем первую дробь так, чтобы после запятой было три цифры: , тогда
Аналогично выполняется вычитание десятичных дробей. Найдем разность чисел 13,1 и 0,37:
При умножении десятичных дробей достаточно перемножить заданные числа, не обращая внимания на запятые (как натуральные числа), а затем в результате справа отделить запятой столько цифр, сколько их стоит после запятой в обоих множителях суммарно.
Например, умножим 2,7 на 1,3. Имеем . Запятой отделим справа две цифры (сумма цифр у множителей после запятой равна двум). В итоге получаем 2,7 1,3=3,51.
Если в произведении получается меньше цифр, чем надо отделить запятой, то впереди пишут недостающие нули, например:

Рассмотрим умножение десятичной дроби на 10, 100, 1000 и т. д. Пусть нужно умножить дробь 12,733 на 10. Имеем . Отделив справа запятой три цифры, получим Но . Значит,
12 733 10=127,33. Таким образом, умножение десятичной дроби на Ю сводится к переносу запятой на одну цифру вправо.
Вообще чтобы умножить десятичную дробь на 10, 100, 1000, надо в этой дроби перенести запятую на 1, 2, 3 цифры вправо Сприписав в случае необходимости к дроби справа определенное число нулей). Например,
Деление десятичной дроби на натуральное число выполняется так же, как деление натурального числа на натуральное, а запятую в частном ставят после того, как закончено деление целой части. Пусть надо разделить 22,1 на 13:

Если целая часть делимого меньше делителя, то в ответе получается нуль целых, например:

Рассмотрим теперь деление десятичной дроби на десятичную. Пусть нужно разделить 2,576 на 1,12. Для этого и в делимом, и в делителе перенесем запятую вправо на столько цифр, сколько их имеется после запятой в делителе (в данном примере на две). Иными словами, умножим делимое и делитель на 100 - от этого частное не изменится. Тогда нужно разделить дробь 257,6 на натуральное число 112, т. е. задача сводится к уже рассмотренному случаю:

Чтобы разделить десятичную дробь на надо в этой дроби перенести запятую на цифр влево (при этом в случае необходимости слева приписывается нужное число нулей). Например, .
Как для натуральных чисел деление не всегда выполнимо, так оно не всегда выполнимо и для десятичных дробей. Разделим для примера 2,8 на 0,09:

В результате получается так называемая бесконечная десятичная дробь. В таких случаях переходят к обыкновенным дробям. Например:
Может оказаться так, что одни числа записаны в виде обыкновенных дробей, другие - в виде смешанных чисел, третьи - в виде десятичных дробей. При выполнении действий над такими числами можно поступать по-разному: либо обратить десятичные дроби в обыкновенные и применить правила действий над обыкновенными дробями, либо обратить обыкновенные дроби и смешанные числа в десятичные дроби (если это возможно) и применить правила действий над десятичными дробями.
В данной статье мы с Вами разберемся, что такое десятичная дробь, какие у нее есть особенности и свойства. Поехали! 🙂
Десятичная дробь является частным случаем обыкновенных дробей (у которой знаменатель кратен 10).
Определение
Десятичными называют дроби, знаменатели которых представляют собой числа, состоящие из единицы и некоторого количества следующих за нею нулей. То есть это дроби со знаменателем 10, 100, 1000 и т.д. Иначе десятичную дробь можно охарактеризовать как дробь со знаменателем 10 или одной из степеней десятки.
Примеры дробей:
, ,
Десятичная дробь записывается иначе, чем обыкновенная. Операции с этими дробями также отличны от операций с обыкновенными. Правила действий над ними в значительной мере приближены к правилами действий над целыми числами. Этим, в частности, обусловлена их востребованность при решении практических задач.
Представление дроби в десятичной записи
В записи десятичной дроби нет знаменателя, в ней отображено число числителя. В общем виде запись десятичной дроби осуществляется по такой схеме:
где Х – целая часть дроби, Y – ее дробная часть, «,» – десятичная запятая.
Для правильного представления обыкновенной дроби в виде десятичной требуется, чтобы она была правильной, то есть с выделенной целой частью (если это возможно) и числителем, который меньше знаменателя. Тогда в десятичной записи целая часть записывается до десятичной запятой (Х), а числитель обыкновенной дроби – после десятичной запятой (Y).
Если в числителе представлено число с количеством знаков, меньшим, чем количество нулей в знаменателе, то в части Y недостающее количество знаков в десятичной записи заполняется нулями впереди цифр числителя.
Пример:![]()
Если обыкновенная дробь меньше 1, т.е. не имеет целой части, то для Х в десятичном виде записывают 0.
В дробной части (Y), после последнего значимого (отличного от нуля) разряда, может быть вписано произвольное количество нулей. На значение дроби это не влияет. И наоборот: все нули в конце дробной части десятичной дроби можно опустить.
Прочтение десятичных дробей
Часть Х читается в общем случае так: «Х целых».
Часть Y прочитывается в соответствии с числом в знаменателе. Для знаменателя 10 следует читать: «Y десятых», для знаменателя 100: «Y сотых», для знаменателя 1000: «Y тысячных» и так далее… 😉
Более корректным считается другой подход к прочтению, основанный на подсчете количества разрядов дробной части. Для этого нужно понимать, что дробные разряды расположены в зеркальном отражении по отношению к разрядам целой части дроби.
Наименования для правильного прочтения приведены в таблице:

Исходя из этого, прочтение должно опираться на соответствие наименованию разряда последней цифры дробной части.
- 3,5 читается как «три целых пять десятых»
- 0,016 читается как «ноль целых шестнадцать тысячных»
Перевод произвольной обыкновенной дроби в десятичную
Если в знаменателе обыкновенной дроби стоит 10 или какая-нибудь степень десятки, то перевод дроби выполняется как описано выше. В остальных ситуациях необходимы дополнительные преобразования.
Существует 2 способа перевода.
Первый способ перевода
Числитель и знаменатель необходимо домножить на такое целое число, чтобы в знаменателе было получено число 10 или одна из степеней десятки. А далее дробь представляется в десятичной записи.
Этот способ применим для дробей, знаменатель которых раскладывается только на 2 и 5. Так, в предыдущем примере ![]() . Если же в разложении присутствуют другие простые множители (например, ), то придется прибегнуть ко 2-му способу.
. Если же в разложении присутствуют другие простые множители (например, ), то придется прибегнуть ко 2-му способу.
Второй способ перевода
2-й способ заключается в делении числителя на знаменатель в столбик или на калькуляторе. Целая часть, если таковая имеется, в преобразовании не участвует.
Правило деления в столбик, приводящее в результате к десятичной дроби, описано ниже (см. Деление десятичных дробей).
Перевод десятичной дроби в обыкновенную
Для этого следует ее дробную часть (справа от запятой) записать в виде числителя, а результат прочтения дробной части – в виде соответствующего числа в знаменателе. Далее, если это возможно, нужно сократить полученную дробь.
![]()
Конечная и бесконечная десятичная дробь
Конечной называют десятичная дробь, дробная часть которой состоит из конечного количества цифр.
Выше все приведенные примеры содержат именно конечные десятичные дроби. Однако не всякую обыкновенную дробь возможно представить в виде конечной десятичной. Если 1-й способ перевода для данной дроби не применим, а 2-й способ демонстрирует, что деление невозможно завершить, значит, получена может быть только бесконечная десятичная дробь.
В полном виде бесконечную дробь записать невозможно. В неполном же виде такие дроби можно представить:
- как результат сокращения до желательного количества разрядов после запятой;
- в виде периодической дроби.
Периодической называется дробь, у которой после запятой можно выделить повторяющуюся бесконечно последовательность цифр.
Остальные дроби называются непериодическими. Для непериодических дробей допустим только 1-й способ представления (округление).
Пример периодической дроби: 0,8888888… Здесь налицо повторяющаяся цифра 8, которая, очевидно, будет повторяться до бесконечности, поскольку нет оснований предполагать иное. Эта цифра называется периодом дроби .
Периодические дроби бывают чистыми и смешанными. Чистой является десятичная дробь, у которой период начинается непосредственно после запятой. У смешанной дроби до периода после запятой имеется 1 или больше цифр.
54,33333… – периодическая чистая десят.дробь
2,5621212121… – периодическая смешанная дробь
Примеры записи бесконечных десятичных дробей:
Во 2-м примере показано, как правильно оформлять период в записи периодической дроби.
Перевод периодических десятичных дробей в обыкновенные
Для перевода чистой периодической дроби в обыкновенную ее период записывают в числитель, а в знаменатель пишут число, состоящее из девяток в количестве, равном количеству цифр в периоде.
![]()
Смешанная периодическая десятичная дробь переводится следующим образом:
- нужно сформировать число, состоящее из числа, стоящего после запятой до периода, и первого периода;
- из полученного числа вычесть число, стоящее после запятой до периода. Итог составит числитель обыкновенной дроби;
- в знаменателе требуется вписать число, состоящее из кол-ва девяток, равных кол-ву цифр периода, а за ними нулей, кол-во которых равно количеству цифр числа, стоящего после запятой до 1-го периода.
![]()
![]()
Сравнение десятичных дробей
Десятичные дроби сравнивают первоначально по их целым частям. Больше та дробь, у которой больше ее целая часть.
Если целые части одинаковы, то сравнивают цифры соответствующих разрядов дробной части, начиная с первого (с десятых). Здесь действует тот же принцип: больше та из дробей, у которой больше разряд десятых; при равенстве цифр разряда десятых сравнивают разряды сотых и так далее.
Поскольку
![]() , поскольку при равных целых частях и равных десятых в дробной части у 2-й дроби больше цифра сотых.
, поскольку при равных целых частях и равных десятых в дробной части у 2-й дроби больше цифра сотых.
Сложение и вычитание десятичных дробей
Десятичные дроби складывают и вычитают так же, как и целые числа, записав соответствующие цифры друг под другом. Для этого нужно, чтобы друг под другом находились десятичные запятые. Тогда единицы (десятки и т.д.) целой части, а также десятые (сотые и т.д.) дробной окажутся в соответствии. Недостающие разряды дробной части заполняют нулями. Непосредственно процесс сложения и вычитания осуществляется так же, как и для целых чисел.
Умножение десятичных дробей
Для умножения десятичных дробей нужно записать их друг под другом, выровняв по последней цифре и не обращая внимания на местоположение десятичных запятых. Затем нужно перемножить числа так же, как и при умножении целых чисел. После получения результата следует пересчитать количество цифр после запятой в обоих дробях и отделить запятой в результирующем числе суммарное количество дробных разрядов. Если разрядов не хватает, то они заменяются нулями.

Умножение и деление десятичных дробей на 10 n
Эти действия просты и сводятся к переносу десятичной запятой. При умножении запятая переносится вправо (дробь увеличивается) на количество знаков, равных количеству нулей в 10 n , где n – произвольная целая степень. То есть некоторое количество цифр переносится из дробной части в целую. При делении, соответственно, запятая переносится влево (число уменьшается), и некоторая часть цифр переносится из целой части в дробную. Если цифр для переноса оказывается недостаточно, то недостающие разряды заполняются нулями.
Деление десятичной дроби и целого числа на целое число и на десятичную дробь
Деление в столбик десятичной дроби на целое число выполняется аналогично делению двух целых чисел. Дополнительно требуется только учет положения десятичной запятой: при сносе цифры разряда, за которым следует запятая, необходимо поставить запятую после текущей цифры формируемого ответа. Далее нужно продолжать делить до получения нуля. Если знаков в делимом для полного деления недостает, в их качестве следует использовать нули.

Аналогично делятся в столбик 2 целых числа, если снесены все цифры делимого, а полное деление еще не завершено. В этом случае после сноса последней цифры делимого ставится десят.запятая в формирующемся ответе, а в качестве сносимых цифр используют нули. Т.е. делимое здесь, по сути, представляют как десятичную дробь с нулевой дробной частью.

Для деления десят.дроби (или целого числа) на десят.число необходимо домножить делимое и делитель на число 10 n , в котором количество нулей равно количеству цифр после десят.запятой в делителе. Таким способом избавляются от десят.запятой в дроби, на которую требуется делить. Далее процесс деления совпадает с описанным выше.
Графическое представление десятичных дробей
Графически десятичные дроби изображаются посредством координатной прямой. Для этого единичные отрезки делят дополнительно на 10 равных долей подобно тому, как на линейке откладываются одновременно сантиметры и миллиметры. Это обеспечивает точное отображение десятичных дробей и возможность объективного их сравнения.
Чтобы дольные деления на единичных отрезках были одинаковыми, следует тщательно продумывать длину самого единичного отрезка. Она должна быть такой, чтобы можно было обеспечить удобство дополнительного деления.
Данный материал мы посвятим такой важной теме, как десятичные дроби. Сначала определимся с основными определениями, приведем примеры и остановимся на правилах десятичной записи, а также на том, что из себя представляют разряды десятичных дробей. Далее выделим основные виды: конечные и бесконечные, периодические и непериодические дроби. В финальной части мы покажем, как точки, соответствующие дробным числам, расположены на оси координат.
Yandex.RTB R-A-339285-1
Что такое десятичная запись дробных чисел
Так называемая десятичная запись дробных чисел может быть использована как для натуральных, так и для дробных чисел. Она выглядит как набор из двух и более цифр, между которыми есть запятая.
Десятичная запятая нужна для того, чтобы отделять целую часть от дробной. Как правило, последняя цифра десятичной дроби не бывает нулем, за исключением случаев, когда десятичная запятая стоит сразу после первого же нуля.
Какие можно привести примеры дробных чисел в десятичной записи? Это может быть 34 , 21 , 0 , 35035044 , 0 , 0001 , 11 231 552 , 9 и др.
В некоторых учебниках можно встретить использование точки вместо запятой (5 . 67 , 6789 . 1011 и др.) Это вариант считается равнозначным, но он более характерен для англоязычных источников.
Определение десятичных дробей
Основываясь на указанном выше понятии десятичной записи, мы можем сформулировать следующее определение десятичных дробей:
Определение 1
Десятичные дроби представляют собой дробные числа в десятичной записи.
Для чего нам нужна запись дробей в такой форме? Она дает нам некоторые преимущества перед обыкновенными, например, более компактную запись, особенно в тех случаях, когда в знаменателе стоят 1000 , 100 , 10 и др. или смешанное число. Например, вместо 6 10 мы можем указать 0 , 6 , вместо 25 10000 – 0 , 0023 , вместо 512 3 100 – 512 , 03 .
О том, как правильно представить в десятичном виде обыкновенные дроби с десятками, сотнями, тысячами в знаменателе, будет рассказано в рамках отдельного материала.
Как правильно читать десятичные дроби
Существуют некоторые правила чтения записей десятичных дробей. Так, те десятичные дроби, которым соответствуют их правильные обыкновенные эквиваленты, читаются почти так же, но с добавлением слов «ноль десятых» в начале. Так, запись 0 , 14 , которой соответствует 14 100 , читается как «ноль целых четырнадцать сотых».
Если же десятичной дроби можно поставить в соответствие смешанное число, то она читается тем же образом, как и это число. Так, если у нас есть дробь 56 , 002 , которой соответствует 56 2 1000 , мы читаем такую запись как «пятьдесят шесть целых две тысячных».
Значение цифры в записи десятичной дроби зависит от того, на каком месте она расположена (так же, как и в случае с натуральными числами). Так, в десятичной дроби 0 , 7 семерка – это десятые доли, в 0 , 0007 – десятитысячные, а в дроби 70 000 , 345 она означает семь десятков тысяч целых единиц. Таким образом, в десятичных дробях тоже существует понятие разряда числа.
Названия разрядов, расположенных до запятой, аналогичны тем, что существуют в натуральных числах. Названия тех, что расположены после, наглядно представлены в таблице:
Разберем пример.
Пример 1
У нас есть десятичная дробь 43 , 098 . У нее в разряде десятков находится четверка, в разряде единиц тройка, в разряде десятых – ноль, сотых – 9 , тысячных – 8 .
Принято различать разряды десятичных дробей по старшинству. Если мы движемся по цифрам слева направо, то мы будем идти от старших разрядов к младшим. Получается, что сотни старше десятков, а миллионные доли младше, чем сотые. Если взять ту конечную десятичную дробь, которую мы приводили в качестве примера выше, то в ней старшим, или высшим будет разряд сотен, а младшим, или низшим – разряд 10 -тысячных.
Любую десятичную дробь можно разложить по отдельным разрядам, то есть представить в виде суммы. Это действие выполняется так же, как и для натуральных чисел.
Пример 2
Попробуем разложить дробь 56 , 0455 по разрядам.
У нас получится:
56 , 0455 = 50 + 6 + 0 , 4 + 0 , 005 + 0 , 0005
Если мы вспомним свойства сложения, то сможем представить эту дробь и в других видах, например, как сумму 56 + 0 , 0455 , или 56 , 0055 + 0 , 4 и др.
Что такое конечные десятичные дроби
Все дроби, о которых мы говорили выше, являются конечными десятичными дробями. Это означает, что количество цифр, расположенное у них после запятой, является конечным. Выведем определение:
Определение 1
Конечные десятичные дроби представляют собой вид десятичных дробей, у которых после знака запятой стоит конечное число знаков.
Примерами таких дробей могут быть 0 , 367 , 3 , 7 , 55 , 102567958 , 231 032 , 49 и др.
Любую из этих дробей можно перевести либо в смешанное число (если значение их дробной части отличается от нуля), либо в обыкновенную дробь (при нулевой целой части). Тому, как это делается, мы посвятили отдельный материал. Здесь просто укажем пару примеров: так, конечную десятичную дробь 5 , 63 мы можем привести к виду 5 63 100 , а 0 , 2 соответствует 2 10 (или любая другая равная ей дробь, например, 4 20 или 1 5 .)
Но обратный процесс, т.е. запись обыкновенной дроби в десятичном виде, может быть выполнен не всегда. Так, 5 13 нельзя заменить на равную дробь с знаменателем 100 , 10 и др., значит, конечная десятичная дробь из нее не получится.
Основные виды бесконечных десятичных дробей: периодические и непериодические дроби
Мы указывали выше, что конечные дроби называются так потому, что после запятой у них стоит конечное число цифр. Однако оно вполне может быть и бесконечным, и в этом случае сами дроби также будут называться бесконечными.
Определение 2
Бесконечными десятичными дробями называются такие, у которых после запятой стоит бесконечное количество цифр.
Очевидно, что полностью такие числа записаны быть просто не могут, поэтому мы указываем лишь часть из них и дальше ставим многоточие. Это знак говорит о бесконечном продолжении последовательности знаков после запятой. Примерами бесконечных десятичных дробей могут быть 0 , 143346732 … , 3 , 1415989032 … , 153 , 0245005 … , 2 , 66666666666 … , 69 , 748768152 … . и т.д.
В «хвосте» такой дроби могут стоять не только случайные на первый взгляд последовательности цифр, но постоянное повторение одного и того же знака или группы знаков. Дроби с чередованием после десятичной запятой называются периодическими.
Определение 3
Периодическими десятичными дробями называются такие бесконечные десятичные дроби, у которых после запятой повторяется одна цифра или группа из нескольких цифр. Повторяющаяся часть называется периодом дроби.
К примеру, для дроби 3 , 444444 … . периодом будет цифра 4 , а для 76 , 134134134134 … – группа 134 .
Какое же минимальное количество знаков допустимо оставить в записи периодической дроби? Для периодических дробей достаточно будет записать весь период один раз в круглых скобках. Так, дробь 3 , 444444 … . правильно будет записать как 3 , (4) , а 76 , 134134134134 … – как 76 , (134) .
В целом записи с несколькими периодами в скобках будут иметь точно такой же смысл: к примеру, периодическая дробь 0 , 677777 – это то же самое, что 0 , 6 (7) и 0 , 6 (77) и т.д. Также допустимы записи вида 0 , 67777 (7) , 0 , 67 (7777) и др.
Во избежание ошибок введем однообразие обозначений. Условимся записывать только один период (максимально короткую последовательность цифр), который стоит ближе всего к десятичной запятой, и заключать его в круглые скобки.
То есть для указанной выше дроби основной будем считать запись 0 , 6 (7) , а, например, в случае с дробью 8 , 9134343434 будем писать 8 , 91 (34) .
Если знаменатель обыкновенной дроби содержит простые множители, не равные 5 и 2 , то при переводе в десятичную запись из них получатся бесконечные дроби.
В принципе, любую конечную дробь мы можем записать в виде периодической. Для этого нам просто нужно добавить справа бесконечно много нулей. Как это выглядит в записи? Допустим, у нас есть конечная дробь 45 , 32 . В периодическом виде она будет выглядеть как 45 , 32 (0) . Это действие возможно потому, что добавление нулей справа в любую десятичную дробь дает нам в результате равную ей дробь.
Отдельно следует остановиться на периодических дробях с периодом 9 , например, 4 , 89 (9) , 31 , 6 (9) . Они являются альтернативной записью схожих дробей с периодом 0 , поэтому их часто заменяют при письме именно дробями с нулевым периодом. При этом к значению следующего разряда добавляют единицу, а в круглых скобках указывают (0) . Равенство получившихся чисел легко проверить, представив их в виде обыкновенных дробей.
К примеру, дробь 8 , 31 (9) можно заменить на соответствующую ей дробь 8 , 32 (0) . Или 4 , (9) = 5 , (0) = 5 .
Бесконечные десятичные периодические дроби относятся к рациональным числам. Иначе говоря, любую периодическую дробь можно представить в виде обыкновенной, и наоборот.
Существуют и дроби, у которых после запятой бесконечно повторяющаяся последовательность отсутствует. В таком случае их называют непериодическими дробями.
Определение 4
К непериодическим десятичным дробям относятся те бесконечные десятичные дроби, в которых после запятой не содержится периода, т.е. повторяющейся группы цифр.
Иногда непериодические дроби выглядят очень похожими на периодические. Например, 9 , 03003000300003 … на первый взгляд кажется имеющей период, однако подробный анализ знаков после запятой подтверждает, что это все же непериодическая дробь. С такими числами надо быть очень внимательным.
Непериодические дроби относятся к иррациональным числам. В обыкновенные дроби их не переводят.
Основные действия с десятичными дробями
С десятичными дробями можно производить следующие действия: сравнение, вычитание, сложение, деление и умножение. Разберем каждое из них отдельно.
Сравнение десятичных дробей может быть сведено к сравнению обыкновенных дробей, которые соответствуют исходным десятичным. Но бесконечные непериодические дроби свести к такому виду нельзя, а перевод десятичных дробей в обыкновенные зачастую является трудоемкой задачей. Как же быстро произвести действие сравнения, если нам нужно сделать это по ходу решения задачи? Удобно сравнивать десятичные дроби по разрядам таким же образом, как мы сравниваем натуральные числа. Этому методу мы посвятим отдельную статью.
Чтобы складывать одни десятичные дроби с другими, удобно использовать метод сложения столбиком, как для натуральных чисел. Чтобы складывать периодические десятичные дроби, необходимо предварительно заменить их обыкновенными и считать по стандартной схеме. Если же по условиям задачи нам надо сложить бесконечные непериодические дроби, то нужно перед этим округлить их до некоторого разряда, а потом уже складывать. Чем меньше разряд, до которого мы округляем, тем выше будет точность вычисления. Для вычитания, умножения и деления бесконечных дробей предварительное округление также необходимо.
Нахождение разности десятичных дробей обратно действию сложения. По сути, с помощью вычитания мы можем найти такое число, сумма которого с вычитаемой дробью даст нам уменьшаемую. Подробнее об этом расскажем в рамках отдельного материала.
Умножение десятичных дробей производится так же, как и для натуральных чисел. Для этого тоже подходит метод вычисления столбиком. Это действие с периодическими дробями мы опять же сводим к умножению обыкновенных дробей по уже изученным правилам. Бесконечные дроби, как мы помним, надо округлить перед подсчетами.
Процесс деления десятичных дробей является обратным процессу умножения. При решении задач мы также пользуемся подсчетами в столбик.
Можно установить точное соответствие между конечной десятичной дробью и точкой на оси координат. Выясним, как отметить точку на оси, которая будет точно соответствовать необходимой десятичной дроби.
Мы уже изучали, как построить точки, соответствующие обыкновенным дробям, а ведь десятичные дроби можно привести к такому виду. Например, обыкновенная дробь 14 10 – это то же самое, что и 1 , 4 , поэтому соответствующая ей точка будет удалена от начала отсчета в положительном направлении ровно на такое же расстояние:
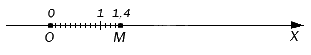
Можно обойтись без замены десятичной дроби на обыкновенную, а взять на основу метод разложения по разрядам. Так, если нам надо отметить точку, координата которой будет равна 15 , 4008 , то мы предварительно представим это число в виде суммы 15 + 0 , 4 + , 0008 . Для начала отложим от начала отсчета 15 целых единичных отрезков в положительном направлении, потом 4 десятых доли одного отрезка, а потом 8 десятитысячных долей одного отрезка. В итоге мы получим точку координат, которой соответствует дробь 15 , 4008 .
Для бесконечной десятичной дроби лучше пользоваться именно этим способом, поскольку он позволяет приблизиться к нужной точке сколь угодно близко. В некоторых случаях можно построить и точное соответствие бесконечной дроби на оси координат: так, 2 = 1 , 41421 . . . , и с этой дробью может быть соотнесена точка на координатном луче, удаленная от 0 на длину диагонали квадрата, сторона которого будет равна одному единичному отрезку.
Если мы находим не точку на оси, а десятичную дробь, соответствующую ей, то это действие называется десятичным измерением отрезка. Посмотрим, как правильно это сделать.
Допустим, нам нужно попасть от нуля в заданную точку на оси координат (или максимально приблизиться в случае с бесконечной дробью). Для этого мы постепенно откладываем единичные отрезки от начала координат, пока не попадем в нужную точку. После целых отрезков при необходимости отмеряем десятые, сотые и более мелкие доли, чтобы соответствие было максимально точным. В итоге мы получили десятичную дробь, которая соответствует заданной точке на оси координат.
Выше мы приводили рисунок с точкой M . Посмотрите на него еще раз: чтобы попасть в эту точку, нужно отмерить от нуля один единичный отрезок и четыре десятых доли от его, поскольку этой точке соответствует десятичная дробь 1 , 4 .
Если мы не можем попасть в точку в процессе десятичного измерения, то значит, что ей соответствует бесконечная десятичная дробь.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
